Первые приспособления для счета
Первыми устройствами для выполнения простых арифметических операций, известными исторической науке, были счеты. Так, среди культурных артефактов древнего мира – Египта, Вавилона, Греции, Рима, Китая можно найти специальный предмет, предназначенный для счета – абак. Абак представляет собой доску, на которой в специальных углублениях расположены небольшие камни. Современные варианты счетов, в виде бусин, нанизанных на проволоку, используются, и посей день для выполнения операций сложения и вычитания.
Рис. 1. Абак — приспособление для счета.
Для более сложных операций, таких как умножение, деление, возведение в степень, вычисление корней и логарифмов, были придуманы различные приспособления. Это логарифмические линейки и таблицы. Логарифмическая линейка была изобретена в 1622 году англичанином Уильямом Отредом, а первая таблица появилась в 1614 году и содержала значения тригонометрических функций.
Механические расчеты
В связи с распространением торговых операций и океаническим судоходством возникла потребность в автоматических вычислениях. В двухтомном собрании рукописей итальянского ученого Леонардо да Винчи (XV–XVI век) содержится описание 13-разрядного суммирующего устройства, состоящего из стержней, на которые крепятся два зубчатых колеса: с одной стороны — большее, с другой — меньшее. Суммирующая машина Леонардо да Винчи, однако, так и осталась одним из нереализованных его проектов.
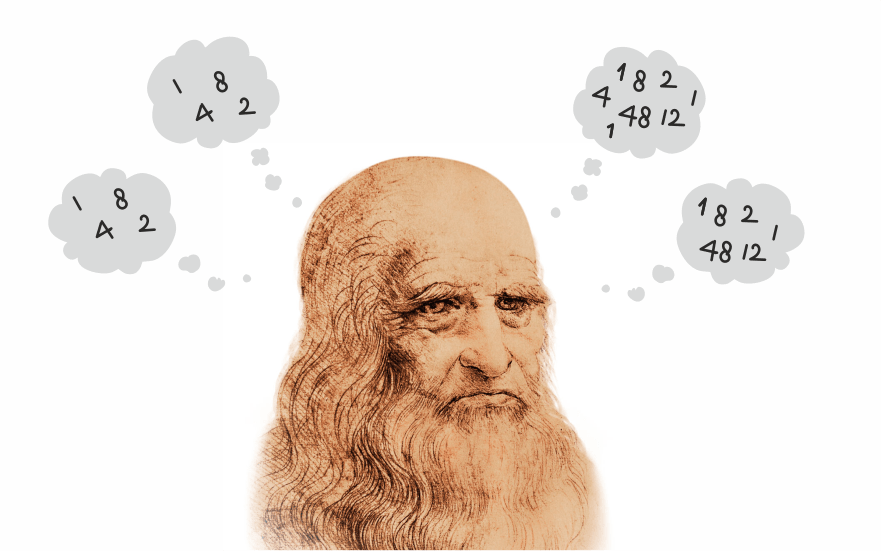
В 1623 году немецкий ученый Вильгельм Шиккард (1592–1635) разработал машину, названную им «счетные часы» и предназначенную для суммирования и умножения шестизначных чисел. Машина Шиккарда состояла из суммирующего устройства, множительного устройства и устройства для записи промежуточных результатов. Устройство было шестиразрядным, в каждом разряде на оси имелись закрепленная шестеренка с десятью зубцами и колесо с одним «пальцем», служившим для передачи десятка в следующий разряд. Были изготовлены два экземпляра машины Шиккарда, однако оба они сгорели во время пожара.
Машины Леонардо да Винчи и Шиккарда были забыты, поэтому длительное время считалось, что создателем первой арифметической машины является французский ученый Блез Паскаль (1623–1662). В 1960-х годах были изготовлены машины Леонардо и Шиккарда, доказавшие свою работоспособность.
Первая модель суммирующей машины Паскаля была создана в 1642 году. В дальнейшем изобретатель неоднократно ее совершенствовал, экспериментируя с материалами и формой деталей. Всего Паскаль создал более 50 моделей машины, названной «Паскалина», из них сохранилось восемь. Машина представляла собой небольшой ящичек с восемью круглыми отверстиями и нанесенной вокруг них круговой шкалой. Шкала крайнего правого отверстия была разделена на 12 частей, соседнего с ним — на 20, остальных — на 10. Такая градуировка была связана с тем, что Паскаль создавал свою машину в помощь отцу, сборщику налогов, и поэтому она соответствовала тогдашней монетной системе (1 ливр = 20 су = 240 денье). В отверстиях располагались зубчатые колеса, число зубьев колеса соответствовало числу делений шкалы данного отверстия. Один из зубцов каждой шестерни был немного удлинен и задевал соседнее колесо. «Паскалина» не получила широкого распространения в связи с ее высокой стоимостью, а также с незначительными вычислительными способностями — в частности, с неудобством выполнения операций вычитания.
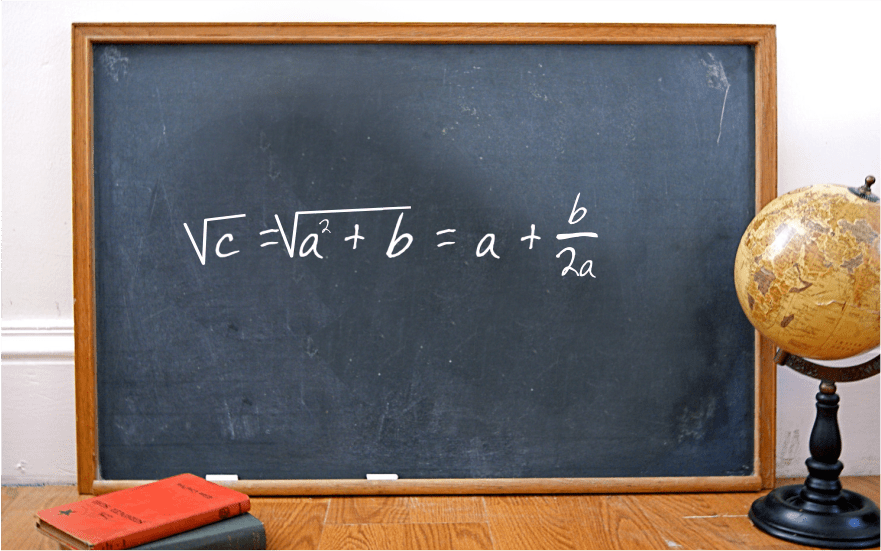
В 1673 году Готфрид Лейбниц создал «ступенчатый вычислитель». В основе арифмометра Лейбница лежит ступенчатый валик (или колесо Лейбница), который впоследствии использовался в конструкции вычислительных машин на протяжении трехсот лет. Ступенчатый валик представлял собой цилиндр с зубцами разной длины, которые взаимодействуют со счётным колесом. Передвигая колесо вдоль валика, его вводили в зацепление с необходимым числом зубцов и обеспечивали установку определённой цифры. Механизм ввода слагаемых находился на подвижной каретке. Конструкция арифмометра включала две вращающиеся рукоятки: одна — для сдвига подвижной каретки, другая — для вращения ступенчатого колеса, что позволяло ускорить повторяющиеся операции сложения, при помощи которых выполнялись умножение и деление. Машина работала с 12-разрядными числами, позволяла производить операции сложения, вычитания, умножения, деления и извлечения квадратного корня.
Появившиеся в XVII–XVIII веках модели арифмометров не нашли широкого распространения, оставшись в основном в виде демонстрационных моделей.
Устройство и обозначение
Абакус (соробан, суаньпань) состоит из рамки и нечетного количества вертикально расположенных спиц. Спицы разделены одной длинной перекладиной (планкой) и представляют собой разряды чисел (единицы, десятки, сотни, тысячи и тд.). Их количество варьирует от 5 до 31, чаще встречаются 13, 17 и 21 разрядные счёты. Большее количество спиц позволяет выполнять арифметические вычисления с большими числами.

На каждой спице расположено 5 костяшек, обозначающие числа от 1 до 9. Одна сверху – над перекладиной (планкой) и соответствует пяти единицам, а 4 под перекладиной, каждая из них приравнивается к единице. Верхнюю принято называть «небесной» – так как она выше остальных, а косточки, которые расположены под перекладиной, называют «земными».
На перекладине нанесены специальные метки – в виде черных, белых или цветных точек. Цвет зависит от цвета самого прибора. Такие метки нанесены не случайно и указывают расположение единиц, тысяч, миллионов.
Современный абакус внешне отличается от далекого предка, однако принцип вычислений остался неизменным. Несмотря на простое устройство, с помощью абакуса возможно выполнять математические операции – от решения несложных заданий на сложение и вычитание до возведения в степень и извлечения корней.
Что такое абакус?
Вот она – эта загадочная счетная машинка.
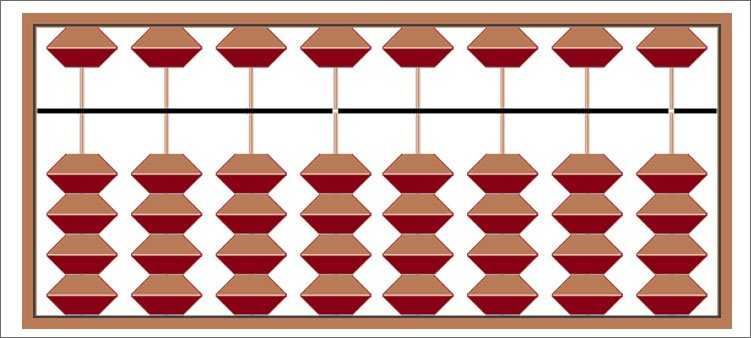
Чем-то напоминает известные многим советские счеты с костяшками. И, насколько я поняла, принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.
Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.
На пальцах
Первые счетные системы человек, вероятно, начал использовать в эпоху позднего палеолита (40–12 тысяч лет назад). Простейшими инструментами для этого служили пальцы. Счет на пальцах широко применялся в Древнем мире и Средневековье, постепенно совершенствуясь и усложняясь.
Естественное распределение пальцев на руках и ногах привело к использованию нескольких разрядов при счете и появлению нескольких систем счисления. Десятеричная система возобладала у народов Евразии. Пятеричная долгое время применялась в Китае, Древней Греции (аттическая система счисления, вытесненная затем десятеричной ионической), Древнем Риме и среди племен тропической Африки. Двадцатеричная система была у ацтеков и майя. Использование при счете четырех пальцев двух рук (большой палец не считался) привело к появлению восьмеричной системы счисления.

В древнем Шумере возникла двенадцатеричная система счисления, в которой счет велся по фалангам четырех пальцев руки. Элементы этой системы еще длительное время использовались в различные периоды истории во многих странах. Так, в Древнем Риме либра (мера веса) равнялась 12 унциям. Введенное денежной реформой Карла Великого (VIII век) соотношение «1 шиллинг = 12 денариев» просуществовало в денежных системах различных государств много столетий. Последними странами, отказавшимися от унаследованного от каролингской реформы соотношения (1 фунт = 20 шиллингов = 240 пенсов), были Великобритания (1971 год) и Нигерия (1973 год). В Древней Руси счет «дюжинами» (большим пальцем руки по фалангам остальных четырех пальцев) применялся в торговле, особенно в Новгороде в XII–XV веках, а традиция считать некоторые товары (носовые платки, карандаши и другие) дюжинами сохранялась до начала XX века.
МЕХАНИЧЕСКИЙ ПЕРИОД
Первые идеи механизации вычислительного процесса появились в конце 15 века. Эскиз суммирующего устройства был разработан не безызвестным Леонардо да Винчи.

Дочь лорда Байрона, великого английского поэта, унаследовала свои математические способности вовсе не от него, а от матери, которую некогда Джордж Гордон Байрон окрестил «принцессой параллелограммов». Родители разошлись навсегда, когда ей не было и года, так что со своим знаменитым отцом она была вовсе не знакома… Двадцати лет она вышла замуж за лорда Кинга, ставшего впоследствии графом Лавлейс, и вела бы обычную жизнь английской леди, когда б не встреча с Чарльзом Бэббиджем.
Таким образом, Ада стала первой в истории программисткой. Не удивительно, что один из современных языков программирования носит ее имя.. Однако Чарльз Бэббидж не смог довести работу до конца – она оказалась слишком сложной для техники того времени. Удалось построить машину по проекту Чарльза Бэббиджа только в 200-летия со дня рождения ученого в Музее науки в Лондоне.
Механические устройства для вычислений
Как техническое средство вычислительная техника берет начало от арифмометров – механических вычислительных устройств, выполняющих поразрядные операции умножения, деления, сложения и вычитания. Известны «Считающие часы», созданные немецким ученым Вильгельмом Шиккардом (1623 г.), «Паскалина» – изобретение французского механика Блеза Паскаля (1642 г.), «Ступенчатый вычислитель» Готфрида Вильгельма Лейбница (1673 г).
Рис. 2. Арифмометр.
Итогом механического периода вычислительных приборов стала разработка английского ученого Чарльза Беббиджа, ставшая прообразом современного компьютера. Задумка аналитической машины, представляла собой проект вычислительного устройства общего назначения, в котором в качестве носителя информации использовались перфокарты. Эта машина, хоть и не была построена при жизни ученого, послужила примером для создания современных компьютеров.
Следующей вехой в развитии вычислительных комплексов явилось использование электромеханических устройств. Первым представителем семейства электромеханических машин стал табулятор Холлерита, разработанный в 1887 г, позволявший автоматизировать и ускорить обработку статистической информации.
История возникновения Абакус
Трудно себе представить счет без цифр. Самым ранним счетным устройством были человеческие пальцы рук, а иногда и ног. Но когда возникла необходимость посчитать что — либо большее, придумали новую счетную систему.
Абакус является одним из многих счетных устройств, изобретенных, чтобы посчитать большие числа.
Суан Пэн
Абакус (Абак), или в китайском языке Suan-Pan, представляет собой деревянную дощечку с шарами. На верхней палубе находилось по 2 косточки, на нижней по 5 (2/5). Так было вплоть до 1850 года, после стиль немного изменился: на верхней палубе осталось по 1 бусинке, а на нижней 5 (1/5).
В японском языке счеты назывались Соробан. У них было соотношение бусинок ¼. Техники подсчета в японской и китайской системе счета похожи, но имеют свои отличия. В нашей стране есть школы, которые обучают как той, так и другой системе подсчета. В статье представлена информация именно о Соробане, так как она активно используется как в Японии, так и в нашей стране для обучения деток.
Были изобретены в 17 веке и используются до сих пор. Дизайн счет напоминает модель пары человеческих рук (каждый ряд имеет 10 бусин, соответствующей 10 пальцам на двух руках).
Модификация Ли Кай Чена
В 1958 году китайский ученый Ли Кай Чен объединил абакус и соробан в одни счеты и опубликовал руководство для новых счетчиков. По словам автора, умножение и деление на много легче использовать с помощью модифицированных счетов. Так можно вычислить даже кубические корни чисел.
На фото видно, что сверху находится японский Соробан, а снизу китайский Суан Пэн.
Какими были египетские цифры?
Египтяне писали иероглифами, то есть использовали рисунки для отображения какой – либо идеи или объекта. Эти рисунки изображали элементы флоры и фауны реки Нил и домашнюю утварь. Цифры они также писали иероглифами. У египтян были знаки для обозначения чисел от 1 до 10.
В древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки для записи чисел 1, 10, 100, 1000, … и специальный иероглиф для обозначения десятков, сотен тысяч, десятков тысяч, сотен тысяч, миллионов и десятков миллионов. Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта.
Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы: .
3.3. Цифры русского народа
Арабские числа в России стали применять, в основном, с XVIII века. До того наши предки использовали славянскую нумерацию. Над буквами ставились титлы (черточки), и тогда буквы обозначали числа.
В одной из русских рукописей XVIII века написано: «. Знай же то, что есть сто и что есть тысяща, и что есть тма, и что есть легион, и что есть леодр. ; . сто есть десятью десять, а тысяща есть десять сот, а тма десять тысящ, а легион есть десять тем, а леодр есть десять легионов. ».
Первые девять чисел записывались так:
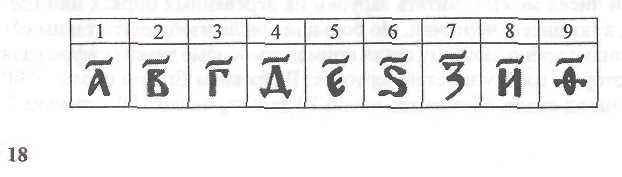
Сотни миллионов назывались «колодами».
Числа от 11 до 19 обозначались так:

Остальные числа записывались буквами слева направо, например, числа 5044 или 1135 имели соответственно обозначение
При записи чисел больших, чем тысячи, в практической деятельности (счете, торговле и т.д.) часто вместо кружков ставили знаки «; Л» перед буквами, обозначавшими десятки и сотни тысяч, например, запись

означает соответственно 500044 и 540004.
В приведенной системе обозначения чисел не шли дальше тысяч миллионов. Такой счет назывался «малый счет». В некоторых рукописях авторами рассматривался и «великий счет», доходивший до числа 10 50 . Далее говорилось: «И более сего несть человеческому уму разумети».
Мир больших чисел
Сколько километров проходит человек за свою жизнь, сколько товаров производится и приходит в негодность ежечасно в пределах города, страны? Сколько времени заняло бы выполнение самым быстрым расчетчиком миллиона вычислительных операций, которые современная вычислительная машина выполняет за. секунду? Во сколько раз скорость пассажирского реактивного самолета превосходит скорость тренированного спортсмена-пешехода? Ответы на эти и тысячи подобных вопросов выражаются числами, занимающими зачастую по числу своих десятичных разрядов целую строку и даже больше.
Для сокращения записи больших чисел давно используется система величин, в которой каждая из последующих в тысячу раз больше предыдущей:
1000 единиц — просто тысяча (1000 или 1 тыс.)
1000 тысяч — 1 миллион (1 млн.)
1000 миллионов — 1 биллион (или миллиард, 1 млрд.)
1000 биллионов — 1 триллион
1000 триллионов — 1 квадриллион
1000 квадриллионов — 1 квинтиллион
1000 квинтиллионов — 1 секстиллион
1000 секстиллионов- 1 септиллион
1000 септиллионов — 1 октиллион
1000 октиллионов — 1 нониллион
1000 нониллионов- 1 дециллион
Таким образом, 1 дециллион запишется в десятичной системе единицей с 3 х 11=33 нулями:
1 000 000 000 000 000 000 000 000 000 000 000.
Как писал Самуил Яковлевич Маршак: «Напрасно думают, что ноль играет маленькую роль».
При записи больших чисел часто используют степень числа 10.
Степень числа — произведение его самого на себя требуемое число раз, которое называется показателем степени (а само число—ее основанием). Например, 3 х 3 = 3 2 (здесь 3 — основание, 2 — показатель степени), 2 х 2 х 2 = 2 3 10 х 10=10 2 =100, 10 5 =10 х 10 х 10 х 10 х 10=100000.
Заметьте, что число нулей степени 10 всегда равно ее показателю:
10 1 = 10, 10 2 = 100, 10 3 = 1000 и т.д.
И еще одно: математики во всем мире давно приняли, что любое число в нулевой степени равно единице (а 0 = 1).
тысяча -10 3 =1 000
миллион -10 6 =1 000 000
биллион — 10 9 = 1 000 000 000
триллион — 10 12 = 1 000 000 000 000
квадриллион — 10 15 = 1 000 000 000 000 000
квинтиллион — 10 18 = 1 000 000 000 000 000 000
секстиллион — 10 21 = 1 000 000 000 000 000 000 000
септиллион — 10 24 =1 000 000 000 000 000 000 000 000
октиллион — 10 27 = 1 000 000 000 000 000 000 000 000 000
Четвертое — 1973 — по настоящее время.
Каково же быстродействие современной микроЭВМ? Оно в 10 раз превышает быстродействие ЭВМ третьего поколения на интегральных схемах, в 1000 раз — быстродействие ЭВМ второго поколения на транзисторах и в 100000 раз — быстродействие ЭВМ первого поколения на электронных лампах.
Краткие характеристики:
Вычислительный элемент — микропроцессоры. Быстродействие — миллиарды операций в секунду. Персональные ЭВМ. Готовые прикладные программы, графический интерфейс, использование технологии мультимедиа. Глобальные компьютерные сети. Это машины, построенные на больших интегральных схемах (БИС). Такие схемы содержат до нескольких десятков тысяч элементов на кристалле. ЭВМ этого поколения выполняют десятки и сотни миллионов операций в секунду. Появляются микропроцессоры, способные обрабатывать числа длиной в 16 и 32 разряда, статическая память у которых емкостью 256 Кбайт и динамическая память емкостью в 1 Мбайт (на сегодняшний день все характеристики увеличились в сотни раз. Представленные здесь — это данные 80-х годов) ЭВМ по своим характеристикам так разнообразны, что их начинают классифицировать на: сверхбольшие ЭВМ (В-7700 — фирма Барроуз, Иллиак-IV — Иллинойский университет, Эльбрус — СССР), большие (универсальные), мини-ЭВМ и микро-ЭВМ (персональные компьютеры — ПК).
Расположение чисел
Теперь о том, как же располагаются числовые линейки.
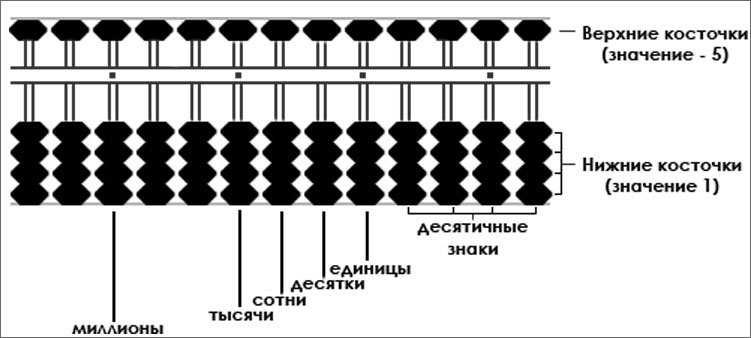
Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?
Давайте посмотрим на примере. Я нарисовала абакус!
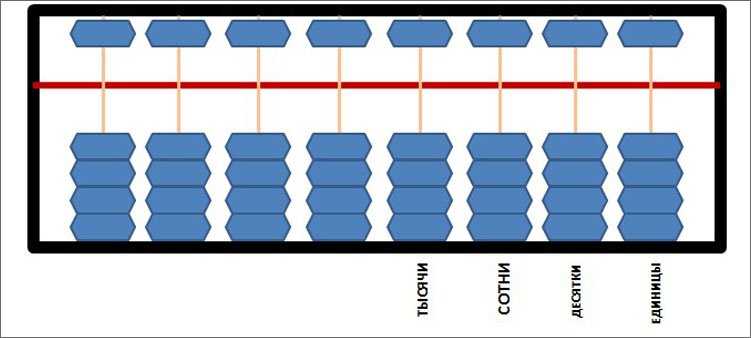
Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на моем рисунке – это единицы.
Так будет выглядеть на абакусе число 3.

Поднимаем к разделительной планке три костяшки на линейке единиц.
Попробуем взять двойное число, например, 15.
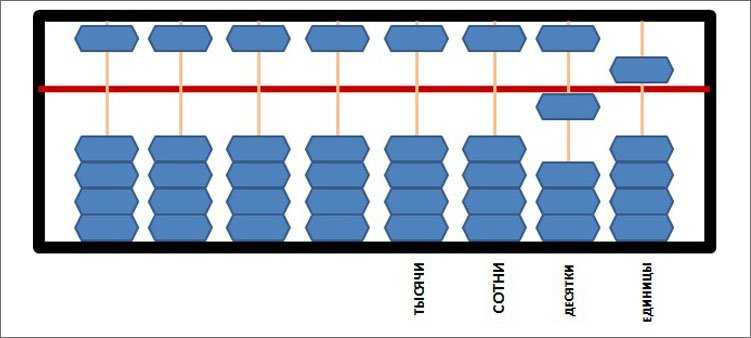
На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

А вот это какое число получилось? Догадаетесь?
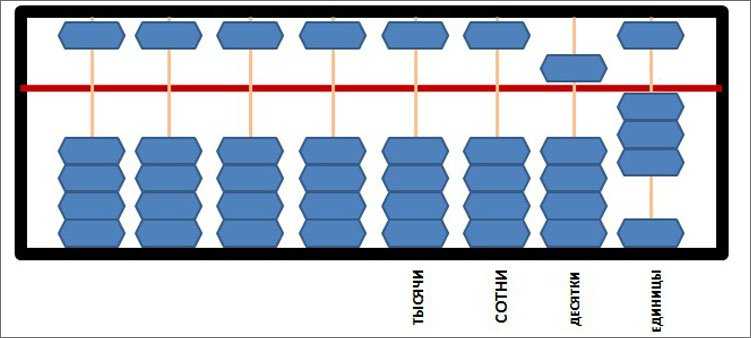
А давайте чего-нибудь посущественнее наберем. Например, 6482!
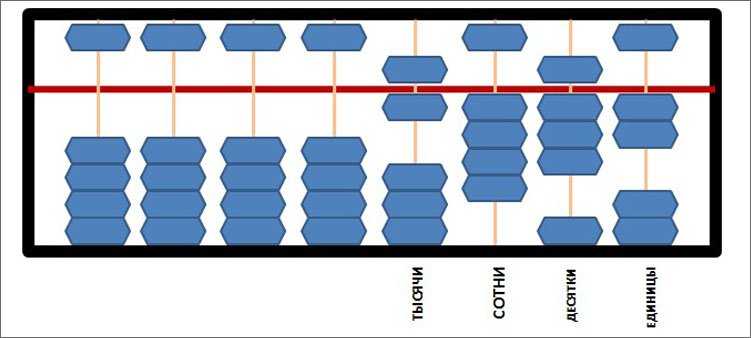
На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?
Числа-символы
Существуют различные теории о происхождении чисел. Классическим примером происхождения чисел считается Древняя Греция. Другой из возможных вариантов происхождения символов чисел – это получение их из символов планет .
0 – абсолют, 1 – его проявление. Все это заключено в Солнце.
2 – двойственность и эмоциональность с ней связанная – свойства Луны.
3 – прошлое, настоящее и будущее время – Сатурн.
4 – четыре стороны света, пространство – Юпитер.
5 – любовь и человек – Венера.
6 – соединение двух треугольников – корень активности, отношений, а также преданность – свойства Марса.
7 – полнота знаний, деталей, особенностей, подвижность – это качества Меркурия.
8 – бесконечность, лунные узлы как точки затмений, во время которых временное соотносится с Вечным.
Источник
Взвешенное решение
С древности своеобразным счетным устройством служили человеку весы (древнейшие весы были обнаружены археологами в Месопотамии и относятся к V тысячелетию до нашей эры). Их применяли для определения количества однородных предметов путем взвешивания вместо пересчета. Неслучайно названия некоторых денежных единиц как в период античности (мина, либральный асс), так и в более позднее время (фунт, французский ливр, итальянская лира) происходят от единиц измерения веса. Чеканившиеся в СССР с 1926 по 1991 годы монеты в 1, 2, 3 и 5 копеек имели вес соответственно в 1, 2, 3 и 5 граммов, что позволяло определять сумму большого числа монет простым взвешиванием.
Важным этапом развития в древности стало появление счетных досок, получивших общее название «абак». Происхождение этого термина не установлено. Возможно, греческое слово ἄβαξ происходит от общесемитского корня слов со значением «пыль». Такое название могло быть связано с тем, что для вычислений использовались доски с углублениями и линиями, на которых в определенном порядке раскладывались однородные предметы (камешки, кости и другие), а чтобы они не скатывались с доски, она покрывалась слоем песка. Считается, что раньше, чем в Греции, абак стали применять в Вавилоне, Египте и Финикии, но археологических подтверждений этому пока не обнаружено. Пифагор (VI век до нашей эры) полагал, что счет с помощью абака должен входить в курс математики.
В Древнем Риме абак появился, вероятно, в V–VI веках и назывался calculi и abaculi (abacus). Римские абаки изготавливались из различных материалов (бронза, слоновая кость, цветное стекло). Бронзовый римский абак, хранящийся в Национальном археологическом музее Неаполя, представляет собой доску с прорезанными в ней щелями, в которых перемещаются костяшки. Семь длинных щелей с четырьмя костяшками, одна — с пятью, над каждой длинной щелью — короткая с одной костяшкой. Над длинными щелями помечены значения разрядов: миллионы, сотни тысяч, десятки тысяч, тысячи, сотни, десятки, единицы, унции (то есть двенадцатые части). В щели, помеченной « », — пять костяшек (то есть 5/12). В правой части абака — щели с пометками, означающие 1/2, 1/4 и 1/6 унции.

Распад и падение Римского государства прервали развитие счетной техники. Абак в Европе был надолго забыт.
В Китае аналог абака — суаньпань — появился в VI веке и постепенно вытеснил традиционную систему счета на палочках. Со временем его устройство менялось, современный вид он приобрел в XVII веке. Суаньпань представляет собой прямоугольную раму, разделенную на две части. В большом отделении («Земля») на каждой проволоке — 5 шариков, в меньшем («Небо») — 2 шарика. Проволоки соответствуют десятичным разрядам, каждый шарик большего поля — единице, меньшего — пяти. На суаньпане можно не только производить четыре арифметических операции, но и извлекать квадратные и кубические корни.
В XV–XVI веках суаньпань был завезен в Японию, где получил название «соробан». В Японии он был модифицирован (последний раз — в 1930 году).
Абак, забытый в Европе после распада Римской империи, вновь получил распространение в X веке благодаря монаху Герберту Орильякскому (938–1003), ставшему впоследствии римским папой Сильвестром II. Герберт во время путешествия в Кордовский халифат познакомился с арабской системой цифр и с абаком.
В XV веке в Англии появилась новая форма абака — «счет на линиях», — распространившаяся в XV–XVI веках по континентальной Европе. Для счета на линиях использовались горизонтально разлинованная доска и металлические жетоны, которые в Германии назывались счетными пфеннигами, в других странах — фишками. Жетоны при счете выкладывались не только на линиях, но и между ними. Разрядность повышалась снизу вверх. Правила счета на линиях излагались во многих учебниках, изданных в XV–XVII веках, счет упоминается в созданных в то время пьесах Шекспира и Мольера.

Программируемые вычислители
Результатом эволюции вычислительных устройств явилось создание электронной вычислительной машины в том виде, в котором мы привыкли ее сейчас видеть. Однако и ЭВМ прошли несколько этапов развития, связанных в первую очередь, с развитием электронной элементной базы:
-
вакуумные лампы;
-
полупроводниковые транзисторы;
-
интегральные микросхемы;
-
микропроцессоры.
К первому поколению вычислительных устройств, базирующемуся на лампах можно отнести ENIAC (США, 1946 г.), ЭВМ БСЭМ-2 (СССР, 1949 г.). Эти машины позволяли производить до 20 тысяч операций в секунду и в качестве устройства ввода использовали перфокарты. Огромные габариты и энергопотребление таких устройств обусловлено особенностями используемой элементной базы.
Самый первый компьютер под названием ENIAC, созданный в 1946 году имел массу более двадцати тонн и занимал огромное помещение площадью порядка 150 квадратных метров.
Рис. 2. ENIAC — первый компьютер на электронных лампах.
Следующий этап развития ЭВМ связан с изобретением полупроводникового транзистора — компактного и экономичного аналога электронной лампы. Быстродействие подобных устройств увеличилось уже до сотен тысяч операций в секунду, а их габариты и энергопотребление значительно снизилось. Что привело к более широкому распространению ЭВМ и упрощению взаимодействия с пользователем. Одним из представителей семейства полупроводниковых машин является ЭВМ БСЭМ-6 (СССР, 1959 г.)
Объединение транзисторных схем в отдельные интегральные микросхемы (ИМС) дало толчок третьему поколению компьютеров. Для этого этапа характерно дальнейшее увеличение производительности и снижение стоимости производства и эксплуатации. А также появление различных периферийных устройств, таких как накопители на магнитных дисках, дисплеи, графопостроители. Среди машин третьего поколения можно выделить IBM-360 (США) и ЕС ЭВМ (СССР).
В настоящее время все компьютеры относятся к четвертому поколению и основаны на использовании микропроцессоров — сверхбольших интегральных схем. Это первый тип компьютеров, который появился в розничной продаже.
Первые компьютеры — это профессия. До того как были созданы компьютерные устройства, компьютерами называли людей, занимавшихся выполнением сложных вычислений на арифмометрах. Как правило, этой профессией овладевали женщины, многие из которых затем с успехом работали программистами.
Что мы узнали?
История развития вычислительной техники берет свое начало в древности. Первыми приспособлениями для вычислений были счеты, логарифмические линейки, арифмометры. Прообразом современного компьютера была аналитическая машина Чарльза Бэббиджа. Развитие компьютерной техники проходило параллельно совершенствованию ее элементной базы: от вакуумных ламп до интегральных микросхем.
-
/5
Вопрос 1 из 5
Слайд 9ЭВМ 1-го поколения (1945-1955) ЭВМ
первого поколения в качестве элементной базы использовали электронные лампы и
реле; оперативная память выполнялась на триггерах, позднее на ферритовых сердечниках; они отличались невысокой надежностью, требовали систем охлаждения и имели значительные габариты. Процесс программирования требовал значительного искусства, хорошего знания архитектуры ЭВМ и ее программных возможностей. На первых порах данного этапа использовалось программирование в кодах ЭВМ (машинный код). Как правило, ЭВМ первого поколения использовались для научно-технических расчетов, а сам процесс программирования больше напоминал искусство, которым занимался весьма узкий круг математиков, инженеров-электриков и физиков.

ДОМЕХАНИЧЕСКИЙ ПЕРИОД
Первым инструментом для счета были руки. Все арифметические операции выполнялись при помощи десяти пальцев рук. В Западной Европе существовала целая система позволяющая представлять на пальцах числа до 9999.
Счет на пальцах, конечно, удобен, только с ним достаточно тяжело хранить информацию.
Ученые назвали этот способ записи чисел единичной («палочной») системой счисления. В ней для записи чисел применялся только один вид знаков – «палочка». В наше время счётные палочки используются для обучения первоклассников.
В Древнем Риме “Саламинская доска” появилась, вероятно, в V-VI вв н. э. и называлась она calculi или abakuli. Для изготовления римского абака, помимо каменных плит, стали использовать бронзу, слоновую кость и даже цветное стекло. В вертикальных желобках, разделенных на два поля, также помещались камешки или мраморные шарики, при этом желобки нижнего поля служили для счета от единицы до пяти. Если в этом желобке набиралось пять шариков, то в верхнее отделение добавлялся один шарик, а из нижнего поля все шарики снимали.
Распространяясь в европейских странах, римский абак постепенно видоизменялся. В XV столетии в Англии появилась новая его форма, называемая “линейчатой доской” (line-board).
Примерно в это же время на Руси получил распространение так называемый “дощатый счет”, завезенный, видимо, купцами из Европы. Он представлял собой рамку с укрепленными горизонтальными веревками, на которые были нанизаны просверленные сливовые или вишневые косточки. Эта рамка разбивалась сначала на четыре, а затем на два счетных поля. В 1658 году в “Переписной книге деловой казны Патриарха Никона” вместо “дощатый счет” употребляется слово “счеты”. А в начале XVIII века счеты приняли свой привычный вид, который в дальнейшем не претерпевал существенных изменений. В них осталось лишь одно счетное поле, на спицах которого размещалось по десять косточек.






























