Нарушение свойства ассоциативности
Вычислим \(\sin(x)\), разложив эту функцию в ряд Тейлора:
$$\sin(x) = x — \frac{x^3}{3!} + \frac{x^5}{5!} — \frac{x^7}{7!} + \frac{x^9}{9!} — …$$
Напишем небольшую функцию, которая будет реализовывать эти вычисления. Тип float вместо double выбран для того, чтобы показать, как быстро накапливается погрешность; никаких дополнительных действий не производится, код исключительно демонстрационный. Целью не является показать, что семи членов ряда недостаточно, цель — показать нарушение свойства ассоциативности операций:
$$a+(b+c)\neq(a+b)+c,$$
хотя свойство коммутативности сохраняется:
$$a + b = b + a.$$
float sine(float x)
{
const int n = 13;
float sine = x;
bool isNegative = true;
for (int i = 3; i <= n; i += 2)
{
sine += (isNegative ?
- (pow(x, i) / Factorial(i))
: (pow(x, i) / Factorial(i)));
isNegative = !isNegative;
}
return sine;
}
Теперь напишем аналогичную функцию, но сделаем так, чтобы те же элементы ряда суммировались в обратном порядке.
float sineReversed(float x)
{
const int n = 13;
float sine = 0;
bool isNegative = false;
for (int i = n; i >= 3; i -= 2)
{
sine += (isNegative ?
- (pow(x, i) / Factorial(i))
: (pow(x, i) / Factorial(i)));
isNegative = !isNegative;
}
sine += x;
return sine;
}
Запустим.
#include <iostream>#include <math.h>
int main()
{
float sine1 = sine(3.1415926f);
float sine2 = sineReversed(3.1415926f);
std::cout << sine1 << std::endl << sine2 << std::endl;
}
Посмотрим на это с точки зрения машины:
\(\sin(\pi) \approx 3{,}141592 — 5{,}16771\)
\(+\ 2{,}55016\)
\(-\ 0{,}599265\)
\(+\ 0{,}0821459\)
\(-\ 0{,}00737043\)
\(+\ 0{,}000466303,\)
\(\sin(\pi) \approx 0{,}000466303 — 0{,}00737043\)
\(+\ 0{,}0821459\)
\(-\ 0{,}599265\)
\(+\ 2{,}55016\)
\(-\ 5{,}16771\)
\(+\ 3{,}141592.\)
До этого момента мнение компьютера и человека, казалось бы, сходится. Но результатом в первом случае окажется \(0{,}0000211327\)(\(2.11327\mathrm{E}{-}005\)), а во втором случае — \(0{,}0000212193\)(\(2.12193\mathrm{E}{-}005\)), совпадают лишь две значащие цифры!
Разгадка проста: у чисел представленного ряда шесть различных(двоичных) порядков: \(1\), \(2\), \(1\), \(-1\), \(-4\), \(-8\), \(-12\). Когда складываются(вычитаются) два числа одного порядка или близких порядков, потери точности, как правило, небольшие. Если бы мы складывали огромное число и много маленьких чисел одного порядка, то мы заметили бы, что лучше в плане точности сперва сложить все маленькие числа, а затем уже прибавить большое. Рассмотрим обратный сценарий: сложим большое и первое маленькое число; поскольку порядки значительно различаются, маленькое число будет(фигурально выражаясь)раздавлено» большим из-за приведения порядков; получилось новое большое число, не очень точное, но пока ещё достаточно близкое к точному результату; к получившемуся большому числу прибавляем второе маленькое, порядки снова значительно различаются, снова маленькое число оказывается раздавленным, уже двежертвы». И так далее. Погрешность накопилась достаточно большая.
Сложение(вычитание) чисел с одинаковым порядком тоже не проходит без округлений, но погрешности, как правило, минимальны.
The Python float has limited precision
Let’s do a little experiment. For extra dramatic effect, try this for yourself first:
>>> 0.3 + 0.1 0.4 >>> 0.1 + 3.8 3.9 >>> 0.1 + 0.2 # What is the output of this last statement?
Did you expect the output to be like any normal person would? I don’t blame you, but you’re wrong! The output is actually . As absurd as this might seem, there’s an explanation.
First of all, some fractional numbers are endless. E.g., when you divide 1 by 3, you can round the result to 0.33, 0.333333333, or 0.333333333333333333. No matter what precision you choose, there will always be more 3’s. Since there’s a limited number of bits to store a float number, many numbers are a best-effort approximation. So floating-point numbers have limited precision because they are stored in a finite amount of memory, sometimes leading to unexpected results when performing arithmetic operations on floating-point numbers.
Solving the limited precision
The limited precision of floats is a fundamental property of how floats are represented in computer memory. Therefore, it is not possible to completely eliminate the issue of limited precision when working with floats.
However, there are a few ways that you can mitigate the effects of limited precision when working with floats in Python:
- Use the module: The module in the Python standard library provides support for decimal floating-point arithmetic. This allows you to work with decimal numbers that have fixed precision, which can be useful for applications that require more precise calculations than what is possible with regular floats. The downside: floats are much faster than using the decimal pacakge.
- Use NumPy: The numpy module is a popular scientific computing library for Python that supports working with arrays of numbers. The numpy module provides a data type called numpy.float128 that allows you to work with higher-precision floating-point numbers than regular floats.
- Round your floats: As mentioned earlier, you can use the function to round a float to a specified number of decimal places. Limiting the number of decimal places used in your calculations can help reduce the strange effects of limited precision, but this method makes your calculations even more imprecise.
Suggested Blogs
Blogs
12128
Top 10 Real-Time SQL Project Ideas: For Beginners & Advanced
Thanks to the big data revolution, the modern business world collects and analyzes millions of bytes of data every day. However, regardless of the bus
Read More
by Pavan Vadapalli
28 Aug 2023
Blogs
5319
Python Free Online Course with Certification
Data Science is now considered to be the future of technology. With its rapid emergence and innovation, the career prospects of this course are increa
Read More
by Pavan Vadapalli
14 Apr 2023
Blogs
5202
13 Exciting Data Science Project Ideas & Topics for Beginners in US
Data Science projects are great for practicing and inheriting new data analysis skills to stay ahead of the competition and gain valuable experience.
Read More
by Rohit Sharma
07 Apr 2023
Blogs
5235
4 Types of Data: Nominal, Ordinal, Discrete, Continuous
Data refers to the collection of information that is gathered and translated for specific purposes. With over 2.5 quintillion data being produced ever
Read More
by Rohit Sharma
06 Apr 2023
Blogs
5273
Best Python Free Online Course with Certification You Should Check Out
Data Science is now considered to be the future of technology. With its rapid emergence and innovation, the career prospects of this course are increa
Read More
by Rohit Sharma
05 Apr 2023
Blogs
5195
5 Types of Binary Tree in Data Structure Explained
A binary tree is a non-linear tree data structure that contains each node with a maximum of 2 children. The binary name suggests the number 2, so any
Read More
by Rohit Sharma
03 Apr 2023
Blogs
5211
42 Exciting Python Project Ideas & Topics for Beginners
Python is an interpreted, high-level, object-oriented programming language and is prominently ranked as one of the top 5 most famous programming langu
Read More
by Rohit Sharma
02 Apr 2023
Blogs
5175
5 Reasons Why Python Continues To Be The Top Programming Language
Introduction
Python is an all-purpose high-end scripting language for programmers, which is easy to understand and replicate. It has a massive base o
Read More
by Rohit Sharma
01 Apr 2023
Blogs
5100
Why Should One Start Python Coding in Today’s World?
Python is the world’s most popular programming language, used by both professional engineer developers and non-designers. It is a highly demanded lang
Read More
by Rohit Sharma
16 Feb 2023
Load More
Описание
CSS свойство позволяет сделать элемент плавающим, смещая его к левому или правому краю родительского элемента, в зависимости от того, какое значение установлено. Если для плавающего элемента явно не установлена ширина (width), то он сжимается по ширине до размеров содержимого.
Браузер обрабатывает код HTML документа двигаясь сверху вниз, когда обработка кода доходит до плавающего элемента, браузер размещает его сначала согласно потоку документа, т.е. под тем элементом где он расположен в коде документа, затем он удаляет плавающий элемент из нормального потока и смещает его на максимально возможное расстояние к левому или правому краю родительского элемента:
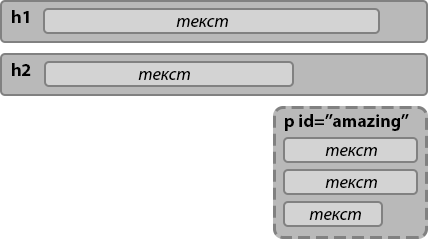
Поскольку плавающий элемент был удалён из потока документа остальные блочные элементы, расположенные в коде после него, смещаются на его место, будто этого элемента там и не было.
Несмотря на то, что плавающий элемент был удалён из нормального потока, на строчное содержимого, тем не менее он влияет. В отличие от блочных элементов, строчное содержимое, расположенное в коде после плавающего элемента, учитывает его границы и обтекает его, то есть происходит обтекание текстом плавающего блока:

Вместо плавающего блока с текстовым содержимым, можно сделать плавающей картинку. В этом случае будет производится обтекание картинки текстом:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Название документа</title>
<style>
p { width: 250px; }
img { float: left; }
</style>
</head>
<body>
<p>
<img src="css.png" width="120" height="120">
С помощью CSS свойства float картинка была сделана плавающей с левой стороны.
Текст, расположенный в HTML коде ниже картинки, будет обтекать картинку
по правой и нижней стороне.</p>
</body>
</html>
Попробовать »
В одном ряду можно размещать более одного плавающего элемента, если это позволяет ширина родительского элемента. Если ширины родительского элемента не хватает, то плавающие элементы, которые не помещаются в ряд с остальными плавающими элементами, будут смещены вниз.
Плавающие элементы не влияют на высоту родителя, то есть, если есть некоторый контейнер, а в нём находятся только плавающие элементы, то высота контейнера будет равна нулю. Решить данную проблему можно следующими способами:
- Задать фиксированную высоту — в тех случаях, когда известно какая должна быть высота контейнера.
- Применить свойство overflow со значением или к контейнеру, тогда плавающие элементы будут учитываться при вычислении высоты контейнера. Этот способ можно использовать когда заранее не известно какая должна быть высота контейнера.
Свойство работает только с блочными элементами, поэтому, если свойство применяется к элементам какого-то другого типа, то они преобразуются к блочному типу.
Примечание: элементы с абсолютным и фиксированным позиционированием игнорируют свойство . Также свойство не оказывает никакого эффекта на флексбоксы.
| Значение по умолчанию: | none |
|---|---|
| Применяется: | ко всем элементам, кроме тех, которые имеют абсолютное или фиксированное позиционирование |
| Анимируется: | нет |
| Наследуется: | нет |
| Версия: | CSS1 |
| Синтаксис JavaScript: | object.style.cssFloat=»left» |
References
A lot of this stuff was observed from small programs I wrote to go back and forth between hex
and floating point (printf-style), and to examine the results of various operations. The bulk
of this material, however, was lifted from Stallings’ book.
-
Computer Organization and Architecture,
William Stallings, pp. 222–234
Macmillan Publishing Company,
ISBN 0-02-415480-6 -
IEEE Computer Society (1985),
IEEE Standard for Binary Floating-Point Arithmetic,
IEEE Std 754-1985. -
Intel Architecture Software Developer’s Manual, Volume 1: Basic Architecture,
(a PDF document downloaded from intel.com).
Controlling Overflow
If the floating element is taller than the element containing it, then the floating element steps out of its container. You can fix this issue with the property. Paired with an value, it stretches the container to be big enough for the floating element.
In the example, we fix the overflow problem using the method:
Without overflow: auto
 In this example, the image is taller than the element containing it, and it is floated, so it overflows outside of its container.
In this example, the image is taller than the element containing it, and it is floated, so it overflows outside of its container.
With overflow: auto
Add a class with overflow: auto; to the containing element, to fix this issue.
Example Copy
The following method is preferred over the way of fixing this issue. It adds hidden content after the parent element (it clears the float).
Most modern websites use this strategy:
Example Copy
Special Values
IEEE reserves exponent field values of all 0s and all 1s to denote special values in the
floating-point scheme.
- Denormalized
-
If the exponent is all 0s, then the value is a denormalized number, which now
has an assumed leading before the binary point. Thus, this represents a number
(−1)s × 0.f × 2−126, where s is the
sign bit and f is the fraction. For double precision, denormalized numbers are of the
form (−1)s × 0.f × 2−1022.As denormalized numbers get smaller, they gradually lose precision as the left bits of the
fraction become zeros. At the smallest non-zero denormalized value (only the least-significant
fraction bit is one), a 32-bit floating-point number has but a single bit of precision,
compared to the standard 24-bits for normalized values. - Zero
-
You can think of zero as a denormalized number (an implicit leading 0 bit) with all 0 fraction
bits. Note that −0 and +0 are distinct values, though they both compare as equal. - Infinity
-
The values +∞ and −∞ are denoted with an exponent of all 1s and a fraction of all 0s. The sign
bit distinguishes between negative infinity and positive infinity. Being able to denote
infinity as a specific value is useful because it allows operations to continue past overflow
situations. Operations with infinite values are well defined in IEEE floating
point. - Not A Number
-
The value NaN (Not a Number) is used to represent a value
that does not represent a real number. NaN’s are represented by a bit pattern with an exponent
of all 1s and a non-zero fraction. There are two categories of NaN: QNaN
(Quiet NaN) and SNaN (Signalling NaN).A QNaN is a NaN with the most significant fraction bit set. QNaN’s propagate freely
through most arithmetic operations. These values are generated from an operation when the
result is not mathematically defined.An SNaN is a NaN with the most significant fraction bit clear. It can be used to signal an
exception when used in operations. SNaN’s can be handy to assign to uninitialized variables to
trap premature usage.Semantically, QNaN’s denote indeterminate operations, while SNaN’s denote
invalid operations.
CSS Advanced
CSS Rounded CornersCSS Border ImagesCSS BackgroundsCSS ColorsCSS Color KeywordsCSS Gradients
Linear Gradients
Radial Gradients
Conic Gradients
CSS Shadows
Shadow Effects
Box Shadow
CSS Text EffectsCSS Web FontsCSS 2D TransformsCSS 3D TransformsCSS TransitionsCSS AnimationsCSS TooltipsCSS Style ImagesCSS Image ReflectionCSS object-fitCSS object-positionCSS MaskingCSS ButtonsCSS PaginationCSS Multiple ColumnsCSS User InterfaceCSS Variables
The var() Function
Overriding Variables
Variables and JavaScript
Variables in Media Queries
CSS Box SizingCSS Media QueriesCSS MQ ExamplesCSS Flexbox
CSS Flexbox
CSS Flex Container
CSS Flex Items
CSS Flex Responsive
Большие числа
Множество чисел, представимых с помощью float(и double), конечно. Из этого, а также из того, что количество разрядов мантиссы весьма ограничено, сразу же следует, что очень большие числа представить не получится; придётся изобретать пути обхода переполнения. Менее очевидным следствием из способа задания числа в виде, описанном выше, является то, что пространство таких чисел не является равномерным. Что это значит?
Возьмём порядок \(e = 0\) и рассмотрим два стоящих подряд числа \(N_{1}\) и \(N_{2}\): у первого мантисса \(m_{1}=00000000000000000000001_{2}\), у второго — \(m_{2}=00000000000000000000010_{2}\).
![]()
![]()
Конвертер, где можно посмотреть побитовое представление действительного числа, с визуализацией
Воспользуемся конвертером: \(N_{1}=1{,}0000001_{10}\), \(N_{2} = 1{,}0000002_{10}\). Разница между ними равна \(0{,}0000001_{10}\).
Теперь возьмём порядок \(e = 127\) и снова рассмотрим два стоящих подряд числа: у первого мантисса \(m_{3}=00000000000000000000001_{2}\), у второго — \(m_{4}=00000000000000000000010_{2}\).
![]()
![]()
\(N_{3}=1{,}701412 \cdot 10^{38}_{10}\), \(N_{4} = 1{,}7014122 \cdot 10^{38}_{10}\). Разница между ними равна \(0{,}0000002 \cdot 10^{38}_{10}\). В рамках этого типа данных нет никакого способа задать некоторое число \(N\), находящееся в интервале между \(N_{3}\) и \(N_{4}\). На секунду, \(0{,}0000002 \cdot 10^{38}\) — это 20 нониллионов, иначе говоря, двойка и 31 ноль! Маленький шаг для мантиссы и огромный скачок для всего числа.
Получается, что, чем больше порядок числа, тем больше разность между ним и следующим числом, которое представимо в рамках типа float. Каждому порядку соответствует одинаковое количество значений мантиссы, следовательно — одинаковое количество представимых чисел:
- порядок \(0\), значения: \(1{,}0…1{,}9999999\),
- порядок \(1\) значения: \(2{,}0…3{,}9999998\),
- порядок \(2\), значения: \(4{,}0…7{,}9999995\),
- порядок \(3\), значения: \(8{,}0…15{,}999999\),
- порядок \(4\), значения: \(16{,}0…31{,}999998\),
- …
- порядок \(126\), значения: \(8{,}507059 \cdot 10^{37}…1{,}7014117 \cdot 10^{38}\),
- порядок \(127\), значения: \(1{,}7014118 \cdot 10^{38}…3{,}4028235 \cdot 10^{38}\).
Каждый из этих диапазонов разбивается на равное количество интервалов. Следовательно, от \(1{,}0\) до \(1{,}9999999\), от \(16{,}0\) до \(31{,}999998\), от \(1{,}7014118 \cdot 10^{38}\) до \(3{,}4028235 \cdot 10^{38}\) находится одинаковое количество доступных значений — \((2^{23} — 2)\)(поскольку мантисса, за исключением скрытого бита, имеет \(23\) бита; минус сами границы).
Всё сказанное в равной степени касается отрицательных чисел и чисел с отрицательными порядками.
Float () Parameters
One of the salient features of the python programming language is that it has rich predefined libraries with numerous methods defined in it. We can use them by just calling the function. While a function is being called, the necessary syntax must be followed and suitable parameters must be passed to the function. Here the term parameters refer to the input arguments given to the method by the user. In the next lines, let us understand more about the parameter of the float() function.
Calling float function: float(X)
Here, the variable X is called the parameter to that function. X can be a normal integer value or any string that has decimal points. An interesting fact about the float() is that the parameter is optional.
Точность чисел с плавающей запятой в Go
В математике некоторые рациональные числа не могут быть точно представлены в форме десятичной дроби. Число 0.33 является лишь приближенным значением дроби 1/3. Неудивительно, что при проведении операций над приближенными значения результат также является приближенным:
1/3 + 1/3 + 1/3 = 1
0.33 + 0.33 + 0.33 = 0.99
Числа с плавающей запятой также страдают от ошибок округления. Разница в том, что машины используют бинарное представление (нули и единицы) вместо десятичного (1-9). В результате компьютеры могут точно передать значение 1/3, но с другими числами могут быть вызваны ошибки округления. Это показано в следующем примере:
Листинг 5
Go
third := 1.0 / 3.0
fmt.Println(third + third + third) // Выводит: 1
piggyBank := 0.1
piggyBank += 0.2
fmt.Println(piggyBank) // Выводит: 0.30000000000000004
|
1 |
third=1.03.0 fmt.Println(third+third+third)// Выводит: 1 piggyBank=0.1 piggyBank+=0.2 fmt.Println(piggyBank)// Выводит: 0.30000000000000004 |
Как видно в примере, числа с плавающей запятой — это не самый лучший выбор для подсчета денег. В качестве альтернативы значение суммы можно хранить в центах, что будут представлены типом целых чисел . Данный тип будет рассмотрен в следующем уроке.
С другой стороны, хотя потерял цент, это не критично для крупных предприятий или покупок. Спрятать ошибки округления можно через использование с точностью в два знака.
Для уменьшения ошибок округления рекомендуется проводить умножение перед делением. Как правило, при осуществлении вычислений в таком порядке результат более точный. Это показано в примерах ниже на примере конвертера температуры:
Листинг 6
Go
celsius := 21.0
fmt.Print((celsius/5.0*9.0)+32, «° F\n»)
fmt.Print((9.0/5.0*celsius)+32, «° F\n»)
// В выводе: 69.80000000000001° F
|
1 |
celsius=21.0 fmt.Print((celsius5.0*9.0)+32,»° F\n») fmt.Print((9.05.0*celsius)+32,»° F\n») // В выводе: 69.80000000000001° F |
Листинг 7
Go
celsius := 21.0
fahrenheit := (celsius * 9.0 / 5.0) + 32.0
fmt.Print(fahrenheit, «° F») // Выводит: 69.8° F
|
1 |
celsius=21.0 fahrenheit=(celsius *9.05.0)+32.0 fmt.Print(fahrenheit,»° F»)// Выводит: 69.8° F |
Вопрос для проверки:
Лучший способ избежать ошибок округления?
Типы данных
Переменные разных типов имеют разные особенности и позволяют хранить числа в разных диапазонах.
| Название | Альт. название | Вес | Диапазон | Особенность |
| 1 байт * | 0 или 1, или | Логический тип | ||
| – | 1 байт | -128… 127 (AVR), 0.. 255 (esp) | Символ (код символа) из таблицы ASCII | |
| – | 1 байт | -128… 127 | Целые числа | |
| 1 байт | 0… 255 | Целые числа | ||
| ** | , | 2 байта | -32 768… 32 767 | Целые числа. На ESP8266/ESP32 – 4 байта! См. ниже |
| ** | , | 2 байта | 0… 65 535 | Целые числа. На ESP8266/ESP32 – 4 байта! См. ниже |
| 4 байта | -2 147 483 648… 2 147 483 647 | Целые числа | ||
| 4 байта | 0… 4 294 967 295 | Целые числа | ||
| – | 4 байта | -3.4E+38… 3.4E+38 | Числа с плавающей точкой, точность: 6-7 знаков | |
| – | 4/8 байт | -1.7E+308.. 1.7E+308 | Для AVR то же самое, что .
На ESP и прочих 32-бит МК – 8 байт, точность – 15-16 знаков |
|
| – | 8 байт *** | -(2^64)/2… (2^64)/2-1 | Целые числа | |
| – | 8 байт *** | 2^64-1 | Целые числа |
- (*) – да, занимает 1 байт (8 бит), так как это минимальная адресуемая ячейка памяти. Есть способы запаковать логические переменные в 1 бит, о них поговорим в другом уроке.
- (**) – на ESP8266/ESP32 и занимает 4 байта, то есть является аналогами типов и !
- (***) – Компилятор также поддерживает 64 битные числа. Стандартные Arduino-библиотеки с переменными этого типа не работают, поэтому можно использовать только в своём коде.
Целочисленные типы
Переменные целочисленных типов нужны для хранения целых чисел. В своей программе рекомендуется использовать альтернативное название типов (второй столбец в таблице выше), потому что:
- Проще ориентироваться в максимальных значениях
- Легче запомнить
- Название более короткое
- Проще изменить один тип на другой
- Размер переменной задан жёстко и не зависит от платформы (например на AVR это 2 байта, а на esp8266 – 4 байта)
Максимальные значения хранятся в константах, которые можно использовать в коде. Иногда это помогает избавиться от лишних вычислений:
- – 255
- – 127
- – 65 535
- – 32 767
- – 4 294 967 295
- – 2 147 483 647
- – 18 446 744 073 709 551 615
- – 9 223 372 036 854 775 807
Логический тип
– логический, он же булевый (придуман Джорджем Булем) тип данных, принимает значения и или и – ложь и правда. Используется для хранения состояний, например включено/выключено, а также для работы в условных конструкциях.
Также переменная типа принимает значение , если присвоить ей любое отличное от нуля число.
bool a = 0; // false bool b = 1; // true bool c = 25; // true
Символьный тип
– тип данных для хранения символов, символ указывается в одинарных кавычках: . По факту это целочисленный тип данных, а переменная хранит номер (код) символа в таблице ASCII:
Отдельный символьный тип данных нужен для удобства работы, чтобы программа могла понять разницу между числом и символом, например для вывода на дисплей (чтобы вывести именно букву A, а не число 65). Из символов можно составлять строки, об этом более подробно поговорим в уроках про символьные строки и String-строки.
Символы и числа
Несмотря на то, что в языке Си символ это по сути целое число, значения например и не равны между собой, потому что символ с точки зрения программы является числом . На практике иногда бывает нужно конвертировать символы чисел в соответствующие им целые числа и наоборот (при работе со строками и буферами вручную), для этого распространены следующие алгоритмы:
- Из символа в число – взять младший ниббл (4 бита):
- Из символа в число – вычесть символ 0:
- Из числа в символ – прибавить символ 0:
Дробные числа
(англ. float – плавающий) – тип данных для чисел с плавающей точкой, т.е. десятичных дробей. Arduino поддерживает три типа ввода чисел с плавающей точкой:
| Тип записи | Пример | Чему равно |
| Десятичная дробь | 20.5 | 20.5 |
| Научный | 2.34E5 | 2.34*10^5 или 234000 |
| Инженерный | 67e-12 | 67*10^-12 или 0.000000000067 |
Выше в таблице есть пометка “точность: 6-7 знаков” – это означает, что в этом типе можно хранить числа, размер которых не больше 6-7 цифр, остальные цифры будут утеряны! Причём целой части отдаётся приоритет. Вот так это выглядит в числах (в комментарии – реальное число, которое записалось в переменную):
float v; v = 123456.654321; // 123456.656250 v = 0.0123456789; // 0.0123456788 v = 0.0000123456789; // 0.0000123456788 v = 123456789; // 123456792.0
Другие особенности float чисел и работу с ними мы рассмотрим в уроках про математические операции и условия.
Python float() Method Usage
Take a look at the example below. Here we try to calculate the area of a rectangle with user-defined length and breadth.
#taking the length and breadth of the rectangle as user inputs
len=input("Enter the length of the rectangle : ")
brdth=input("Enter the breadth of the rectangle : ")
#at this point both len and brdth are holding str values
area=float() #area declared as float() object
#len and brdth type-casted to float for * operation
area=float(len)*float(brdth)
#area is calculated
print("The area of the given rectangle is : ",area)
print("type of area= ",type(area))
Output:
float() Example
In this code above,
- At first, we take the length as well as the breadth of the rectangle as user inputs. Which by default is stored as string type values
- Then we declare a variable , an object of float type, which is going to store the area of the rectangle in future
- After that, we explicitly convert the string type and parameters into floating-point type using the method. And further calculate the area i.e., len*brdth, and print the same
- Finally, we print the of area, which as expected turns out as float type itself
float, double или decimal?
Работа со значениями с плавающей запятой в программировании всегда вызывала много вопросов и проблем. Например, C# имеет по крайней мере три типа данных для работы с нецелыми / нецелыми числами:
- float(псевдоним System.Single)
- double(псевдоним System.Double)
- decimal(псевдоним System.Decimal)
Основные различия может быть немного трудно понять, если у вас нет достаточно знаний о внутренней работе компьютера, так что давайте здесь придерживаться более практических вещей.
В общем случае разница между типами данных float, double и decimal заключается в точности и, следовательно, в объеме памяти, используемой для их хранения. float является наименее затратным — он может представлять собой число до 7 цифр. double более точен, До 16 знаками, десятичная дробь самая точная, аж до максимумом в 29 знаков.
Вы можете задаться вопросом, для чего вам нужна вся эта точность, но ответ — «математика». Классический пример, чтобы понять разницу деления 10 на 3. Большинство из нас сделает это в голове и скажет, что результат 3.33, но многие люди также знают, что это не совсем точно. Реальный ответ 3.33, а затем количество дополнительных 3-ек — сколько, при выполнении этого расчета с c#, определяется типом данных. Проверьте этот пример:
Я произвожу точно такие же вычисления, но с различными типами данных. Результат будет выглядеть следующим образом:
Разница довольно ясна, но сколько точности вычисления вам действительно нужно для большинства задач?
Как выбрать
Прежде всего, вы должны учитывать, сколько знаков вам нужно хранить. float может содержать только 7 цифр, так что если вам нужно большее число, вы можете пойти с double или decimal вместо этого.
Во — вторых, как float, так и double будут представлять значения в приближении к фактическому значению-другими словами, они могут быть несопоставимы с самой последней цифрой. Это также означает, что, как только вы начнете делать все больше и больше вычислений с этими переменными, они могут быть уже не такими точными, что в основном означает, что два значения, которые должны проверяться как равные, внезапно не окажутся равными.
Таким образом, для ситуаций, где точность является основной проблемой, вы должны применять тип decimal . Отличный пример для представления финансовых чисел (денег) — вы не хотите добавлять 10 сумм в свой Бухгалтерский учет, просто чтобы узнать, что результат не такой, как вы ожидали. С другой стороны, если производительность более важна, вы должны применить float (для небольших чисел) или double (для больших чисел). A decimal , благодаря своей дополнительной точности, намного медленнее, чем float — некоторые тесты показывают, что он до 20 раз медленнее!









![Difference between float vs double data types [updated]](http://rwvt.ru/wp-content/uploads/c/8/8/c88209bb2f500ab54d0d85eab75788c3.jpeg)


















