Объем пирамиды

Свойства пирамиды

Пирамида с равным боковыми ребрами

Все углы между боковыми ребрами и основанием пирамиды равны.

Свойство 2

Вокруг основания пирамиды можно описать окружность, центр которой будет совпадать с проекцией вершины на ее основание.

• Точка F– проекция вершины E на основание ABCD; одновременно является центром этого основания.
• R– радиус описанной окружности.

Боковые грани пирамиды наклонены к основанию под одинаковым углом

Примечание: для перечисленных выше свойств верны и обратные формулировки. Например, для Свойства 1: если все углы между боковыми ребрами и плоскостью основания пирамиды равны, значит эти ребра имеют одинаковую длину.

Виды пирамид

В зависимости от количества углов в основании пирамиды ее можно назвать треугольной, четырехугольной и так далее (рис. 2).

Рисунок 2.

Еще один вид пирамид — правильная пирамида.

Определение 2

Пирамида, в основании которой лежит правильный многоугольник и высота пирамиды падает в его центр называется правильной пирамидой (рис. 3).

Рисунок 3. Правильная пирамида

Введем и докажем свойство правильной пирамиды.

Теорема 1

Все боковые грани правильной пирамиды являются равнобедренными треугольниками, которые равны между собой.

Доказательство.

Рассмотрим правильную $n-$угольную пирамиду с вершиной $S$ высотой $h=SO$. Опишем вокруг основания окружность (рис. 4).

Рисунок 4.

Рассмотрим треугольник $SOA$. По теореме Пифагора, получим

\

Очевидно, что так будет определяться любое боковое ребро. Следовательно, все боковые ребра равны между собой, то есть все боковые грани — равнобедренные треугольники. Докажем, что они равны между собой. Так как основание — правильный многоугольник, то основания всех боковых граней равны между собой. Следовательно, все боковые грани равны по III признаку равенства треугольников.

Теорема доказана.

Введем теперь следующее определение, связанное с понятием правильной пирамиды.

Определение 3

Апофемой правильной пирамиды называется высота её боковой грани.

Очевидно, что по теореме один все апофемы равны между собой.

Теорема 2

Площадь боковой поверхности правильной пирамиды определяется как произведение полупериметра основания на апофему.

Доказательство.

Обозначим сторону основания $n-$угольной пирамиды через $a$, а апофему через $d$. Следовательно, площадь боковой грани равна

\

Так как, по теореме 1, все боковые стороны равны, то

\

Теорема доказана.

Еще один вид пирамиды — усеченная пирамида.

Определение 4

Если через обычную пирамиду провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченной пирамидой (рис. 5).

Рисунок 5. Усеченная пирамида

Боковыми гранями усеченной пирамиды являются трапеции.

Теорема 3

Площадь боковой поверхности правильной усеченной пирамиды определяется как произведение суммы полупериметров оснований на апофему.

Доказательство.

Обозначим стороны оснований $n-$угольной пирамиды через $a\ и\ b$ соответственно, а апофему через $d$. Следовательно, площадь боковой грани равна

\

Так как все боковые стороны равны, то

\

Теорема доказана.

Правильная пирамида в геометрии: определение и основные свойства

Правильная пирамида — это геометрическое тело, состоящее из многоугольной основы и треугольных граней, которые сходятся в одной точке, называемой вершиной пирамиды. Основа пирамиды может быть различной формы — треугольник, прямоугольник, пятиугольник и т. д. Все боковые грани пирамиды должны быть одинаковыми треугольниками, то есть иметь равные стороны и равные углы между сторонами.

Основная характеристика правильной пирамиды — это её высота, которая является расстоянием между основанием пирамиды и вершиной. Также важным понятием является высота боковой грани пирамиды, которая является расстоянием от вершины пирамиды до середины стороны основания.

Чаще всего при изучении правильной пирамиды используются понятия её объёма и площади поверхности. Объём правильной пирамиды вычисляется по формуле V = (1/3) * S * h, где S — площадь основы пирамиды, h — высота пирамиды. Площадь поверхности правильной пирамиды вычисляется по формуле S = S_основы + S_{боковых граней}, где S_основы — площадь основы пирамиды, S_{боковых граней} — сумма площадей боковых граней.

К основным свойствам правильной пирамиды относятся:

• Все боковые грани правильной пирамиды равны между собой;
• Углы между боковыми гранями равны между собой;
• Боковые грани пирамиды пересекаются по общим рёбрам;
• Высота боковой грани является расстоянием от вершины до середины стороны основания;
• Площадь поверхности пирамиды может быть вычислена как сумма площади основания и площади боковых граней;
• Объём пирамиды вычисляется по формуле, в которой участвуют площадь основания и высота.

Правильные пирамиды имеют множество применений в геометрии, архитектуре и инженерии. Они служат основой для построения и проектирования различных сооружений и конструкций, а также используются в математических расчётах и моделировании.

изображений пирамиды PNG изображения | Векторные и PSD файлы

роскошная фоторамка для фотографий png

2000 * 2000

реалистичная фоторамка вектор 3d набор квадратных размеров a3 a4 деревянная пустая рамка для фотографий висит на прозрачном фоне с мягкой прозрачной тенью шаблон дизайна для макета

5000 * 5000

набор различных изображений для бровей

1024 * 1369

золотая рамка теплый цвет рамка рамка фото рамка золото

2000 * 2000

набор декоративных старинных рамок и бордюров набор золотых фото рамка с углом Таиланд линия для изображения вектор дизайн украшения шаблон стиль границы дизайн шаблон тайский стиль искусства

8333 * 8333

запись интерфейса изображения

1200 * 1200

современный плоский геометрический новый продукт промо ция социальные медиа дизайн изображения

1200 * 1200

компьютерный монитор изображение бесплатно png прозрачный слой материала

2000 * 2000

набор декоративных старинных рамок и бордюров набор золотой фоторамки с угловой линией Таиланда для дизайна векторных изображений украшение узор стиль границы дизайн узор тайский стиль искусства

8333 * 8333

сигары сигареты картинки

2501 * 2501

орел крылатый орел картинки бесплатно png прозрачный слой материала

2000 * 2000

цветущие красные розы цветочная фотография фотография изображение

2500 * 2500

вектор металлическая рамка рисунка золотая рамка иллюстрация

2500 * 2500

изображение компаса

2501 * 2501

золотая рамка теплый цвет фоторамка золото

1500 * 1500

крылья ангела картина

2000 * 2000

золотой классический орнамент фоторамка бордюрный эффект

800 * 800

набор изображений разных ресниц

1024 * 1369

ностальгические бумажные рваные бумажные этикетки картинки

* 1369

ручная роспись золотых фестивалей макара санкранти

1200 * 1200

рисованные плоские рисунки фестиваля макара санкранти

1200 * 1200

рисованные плоские плоские рисунки макара санкранти 1200 *

фестивали

изображение непрерывной линии минималистских животных-бабочек

4000 * 4000

вектор прямоугольная кривая звуковой волны png изображение

1200 * 1200

рисованной красочный макара санкранти фестиваль групповое изображение

1200 * 1200

питание пирамида здорового питания

902 70 3000 * 3000

лампочка векторное решение знак значок лампочки яркое изображение 3d реалистичная прозрачная иллюстрация

5000 * 5000

набор декоративных старинных рамок и бордюров набор золотая фоторамка с угловой линией Таиланда цветочные для вектора изображения дизайн украшение узор стиль границы дизайн узор тайский стиль арт

5000 * 5000

круглый значок контакта вектор материал изображение

1024 * 1369

висит фоторамка

1200 * 1200

винтаж золотой современный бордюр теплый цвет бордюр рамка фоторамка золото

1200 * 1200

фоторамка европейский стиль фоторамка масляная живопись

2000 * 2000

Различные типы правильных пирамид

Правильная пирамида — это геометрическая фигура, которая имеет особую структуру и внешний вид. Особенность правильной пирамиды заключается в том, что ее основание является многоугольником, все грани пирамиды равны между собой и пересекаются в одной точке, называемой вершиной.

Существует несколько различных типов правильных пирамид, включая:

1. Тетраэдр: это самый простой тип правильной пирамиды, который имеет четырехугольное основание и четыре треугольные грани. Примером тетраэдра может служить пирамида с триугольным основанием, такая как Гизская пирамида в Египте.

2. Гексаэдр: он также известен как куб и имеет шестигранный вид. Каждая грань куба является квадратом, и все грани куба равны между собой. Кубы часто используются в геометрических моделях и конструкциях.

3. Октаэдр: это правильная пирамида с восемью треугольными гранями. Основание октаэдра представляет собой равносторонний треугольник, а вершины пирамиды соединены с центром основания.

4. Додекаэдр: это правильная пирамида с двенадцатью пятиугольными гранями. Все пятиугольные грани додекаэдра равны между собой. Додекаэдр также является одним из пяти платонических тел, которые были открыты и изучены Древней Грецией.

5. Икосаэдр: это правильная пирамида с двадцатью треугольными гранями. Основание икосаэдра является правильным пятиугольником, а вершины пирамиды соединены с центром основания. Икосаэдр также является одним из пяти платонических тел.

Каждый из этих типов правильных пирамид имеет свою уникальную структуру и форму. Они находят применение в различных областях, начиная от математических моделей до архитектурных сооружений.

Примеры решения задач

Задача 1

Дана правильная треугольная пирамида. Сторона основания пирамиды равна 2. Найдите площадь основания пирамиды.

Решение: пирамида правильная и треугольная, значит, в основании равносторонний треугольник. Тогда площадь основания пирамиды находится по формуле: . Нам дана сторона , тогда

Ответ:

Задача 2

Строитель решил построить здание в форме правильной шестиугольной пирамиды, для основания пирамиды у него есть доски, каждая площадью 0,5
м2. Сколько досок ему понадобится, если сторона основания пирамиды равна 6 м?

Решение:

Рассчитаем площадь основания правильной шестиугольной пирамиды. Для этого воспользуемся формулой: . Подставим в нее значение стороны . Получим:
м2.

Теперь подсчитаем, сколько нам понадобится досок: .

Ответ: 108 досок.

Задача 3

Основанием пирамиды является прямоугольный равнобедренный треугольник, с катетом, равным 4. Найдите площадь основания пирамиды.

Решение: иными словами — нас просят определить площадь прямоугольного равнобедренного треугольника. Так как треугольник прямоугольный и равнобедренный, то один из катетов будет основанием треугольника, а другой — высотой. Определяем площадь по формуле:

.

Ответ: 8

Задача 4

Условие. Найти общую площадь пирамиды, если в его основании лежит равносторонний треугольник со стороной 4 см, а апофема имеет значение √3 см.

Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см2.

Для треугольника в основании получится такое значение площади: (42*√3) / 4 = 4√3 см2.

Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см2.

Ответ. 10√3 см2.

Задача 5

Условие. Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.

Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.

Первые расчеты просты и приводят к такому числу: 49 мм2. Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16)2) = √2985,9375 = 54,644 мм2. Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.

Получается: 49 + 4*54,644 = 267,576 мм2.

Ответ. Искомое значение 267,576 мм2.

Задача 6

Условие. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть прямоугольный треугольник. Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(32 + 42) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+62 = 96 (см2).

Ответ. 96 см2.

Задача 7

Условие. Дана правильная шестиугольная пирамида. Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*222) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см2.

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61)2)=√435600=660 см2. Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см2. Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см2.

Ответ. Основания — 726√3 см2, боковой поверхности — 3960 см2, вся площадь — 5217 см2.

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной квадратной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Скажем сразу, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Если предположить, что известны высота h пирамиды и длина a стороны квадратного основания, то боковое ребро b будет равно:

б = √(а2 / 2 + h2)

Теперь приведем формулу длины ab апофемы (высоты треугольника, опущенного на сторону основания):

аб = √(а2 / 4 + h2)

Ясно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно использовать для определения всех четырех линейных свойств, если известны два других параметра, например ab и h.

Площадь и объем фигуры

Это еще два важных свойства правильной квадратной пирамиды. Основание фигуры имеет следующую площадь:

Итак = а2

Эту формулу знает каждый школьник. Площадь боковой поверхности, которую образуют четыре одинаковых треугольника, можно определить через апофему ab пирамиды следующим образом:

Сб = 2×а×аб

Если ab неизвестно, то его можно определить по формулам из предыдущего раздела через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры равна сумме площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

Расчетная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

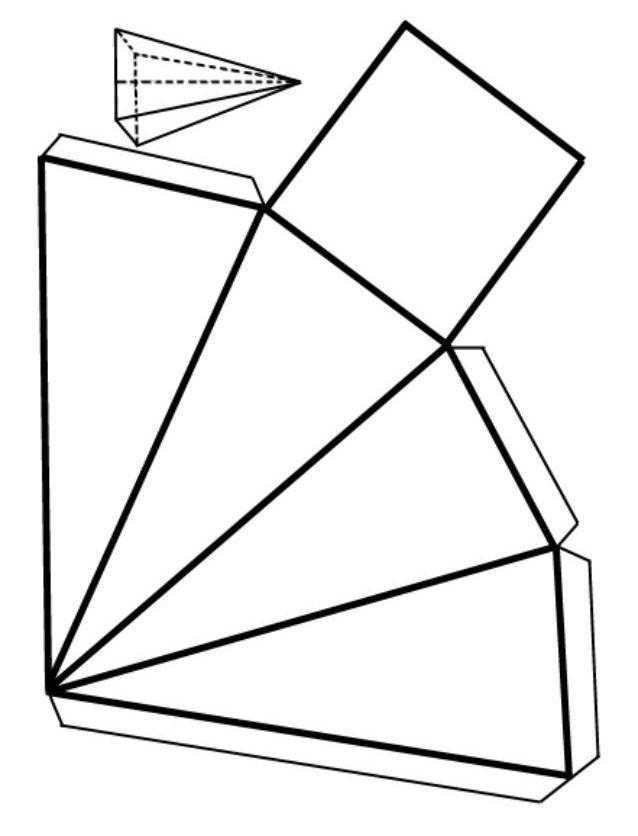
Описание свойств правильной квадратной пирамиды будет неполным, если не рассмотреть формулу определения объема. Это значение для рассматриваемой пирамиды рассчитывается следующим образом:

V = 1/3 × ч × а2

То есть V равно третьей части произведения высоты фигуры на площадь основания удила.

Теория

Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019

Для решения задач понадобится знать теоремы равнобедренного треугольника:

Равнобедренный треугольник

Основные свойства

1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.

2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.

Пирамида

Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида

Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Треугольная пирамида

Необходимые знания для нахождения высоты

1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).

2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.

3Что такое правильные многоугольники: виды, свойства, формулы.

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

Формулы

Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

Объем пирамиды

Нахождение высоты в правильной пирамиде

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Треугольная пирамида

Задача 1

В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Ответ: 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Ответ: 6

Четырехугольная пирамида

Четырехугольная пирамида

Задача 1

Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

OL = ½*12 = 6

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

MO = 8

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Ответ: 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

Площадь равнобедренного треугольника

36 = ½ * 4 *h

36 = 2h

H = 18

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Ответ: 12

Площади поверхностей

Основные геометрические задачи, которые приходится решать в школьном курсе геометрии, это нахождение площадей поверхности и объема у пирамиды.

Значение площади поверхности различают двух видов:

• площади боковых элементов,
• площади всей поверхности.

Из самого названия понятно, о чём идёт речь. Боковая поверхность включает в себя только боковые элементы. Из этого следует, что для ее нахождения необходимо просто сложить площади боковых плоскостей, то есть площади равнобедренных 3-угольников. Попробуем вывести формулу площади боковых элементов:

1. Площадь равнобедренного 3-угольника равна Sтр=1/2(aL), где а – сторона основания, L – апофема.
2. Количество боковых плоскостей зависит от вида k-го угольника в основании. К примеру, правильная четырехугольная пирамида имеет четыре боковые плоскости. Следовательно, необходимо сложить площади четырёх фигур Sбок=1/2(aL)+1/2(aL)+1/2(aL)+1/2(aL)=1/2*4а*L. Выражение упрощено таким способом потому, что значение 4а=Росн, где Росн – периметр основы. А выражение 1/2*Росн является её полупериметром.
3. Итак, делаем вывод, что площадь боковых элементов правильной пирамиды равна произведению полупериметра основания на апофему: Sбок=Росн*L.

Площадь полной поверхности пирамиды состоит из суммы площадей боковых плоскостей и основания: Sп.п.= Sбок+Sосн.

Что касается площади основания, то здесь формула используется соответственно виду многоугольника.

Объем правильной пирамиды равен произведению площади плоскости основания на высоту, разделенную на три: V=1/3*Sосн*Н, где Н – высота многогранника.

Что такое правильная пирамиды в геометрии

Свойства правильной четырехугольной пирамиды

Определение

К примеру, Эвклид определял ее как телесную фигуру, состоящую из плоскостей, которые, начиная от одной, сходятся в определенной точке.

Герон представил более точную формулировку. Он настаивал на том, что это фигура, которая имеет основание и плоскости в виде треугольников, сходящиеся в одной точке.

Опираясь на современное толкование, пирамиду представляют, как пространственный многогранник, состоящий из определённого k-угольника и k плоских фигур треугольной формы, имеющую одну общую точку.

Разберемся более подробно, из каких элементов она состоит:

• k-угольник считают основой фигуры;
• фигуры 3-угольной формы выступают гранями боковой части;
• верхняя часть, из которой берут начало боковые элементы, называют вершиной;
• все отрезки, соединяющие вершину, называют рёбрами;
• если из вершины на плоскость фигуры опустить прямую под углом в 90 градусов, то её часть, заключенная во внутреннем пространстве — высота пирамиды;
• в любом боковом элементе к стороне нашего многогранника можно провести перпендикуляр, называемый апофемой.

Число рёбер вычисляется по формуле 2*k, где k – количество сторон k-угольника. Сколько граней у такого многогранника, как пирамида, можно определить посредством выражения k+1.

Важно! Пирамидой правильной формы называют стереометрическую фигуру, плоскость основы которой является k-угольник с равными сторонами.

Пирамида. Прямоугольная пирамида. Правильная пирамида. Объем пирамиды. Тетраэдр

Факт 1. Про произвольную пирамиду \(PA_1A_2. A_n\) \(\bullet\) Многоугольник \(A_1. A_n\) – основание; треугольники \(PA_1A_2, PA_2A_3\) и т.д. – боковые грани; точка \(P\) – вершина; отрезки \(PA_1, PA_2, . A_1A_2\) и т.д. – ребра. \(\bullet\) Если в основании пирамиды лежит треугольник, то она называется \(>>>\) . \(\bullet\) \(>>>\) — это треугольная пирамида, все грани которой – равносторонние треугольники. \(\bullet\) Высота пирамиды – перпендикуляр, опущенный из вершины \(P\) к основанию. \(\bullet\) \(>>>\) \ где \(S_>\) – площадь основания, \(h\) – высота пирамиды. \(\bullet\) Площадь боковой поверхности – сумма площадей всех боковых граней. Площадь полной поверхности – сумма площади боковой поверхности и площади основания.

\(\bullet\) Заметим, что принято записывать название пирамиды, начиная с вершины.

Факт 2. Про прямоугольную пирамиду \(\bullet\) Пирамида называется прямоугольной, если одно из ее боковых ребер ( \(SR\) ) перпендикулярно основанию (оно же будет и высотой). \(\bullet\) Грани, образованные этим ребром, будут представлять собой прямоугольные треугольники ( \(\triangle SMR, \triangle SPR\) ).

Факт 3. Про правильную пирамиду \(\bullet\) Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:

\(\sim\) боковые ребра равны; \(\sim\) высота пирамиды проходит через центр описанной около основания окружности; \(\sim\) боковые ребра наклонены к основанию под одинаковым углом. \(\bullet\) Заметим, что у правильных многоугольников центры описанной и вписанной окружностей совпадают.

\(\bullet\) Заметим, что у правильной пирамиды все боковые грани – равные равнобедренные треугольники. Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой.

Определение

Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
AO — радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)

Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC)

Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).