Геометрия

Вписанный в шар цилиндр

Предположим, что тел: шар и вписанный в шар цилиндр.

Цилиндр записывают в окружность, если окружность его основания лежит на поверхности окружности. В этом случае также говорят, что вокруг цилиндра описана окружность. Центр шара лежит на оси цилиндра.

Так же, как и при решении задач о шаре, вписанном в цилиндр, чаще всего рассматривают сечение совмещенной плоскости, проходящей через ось цилиндра. Это сечение представляет собой вписанный в периметр прямоугольник, стороны которого равны высоте конуса и диаметру его основания. Центр окружности лежит на пересечении диагоналей прямоугольника.

Рассмотрим пример такого осевого сечения. Здесь точка O — центр, описанный вокруг цилиндра шара, BD — диаметр шара, OD=R — радиус шара, AB=H — форма и высота цилиндра, AD — диаметр цилиндра, FD=r — радиус цилиндра.

угол ABD = frac{1}{2}угол AOD» src=»https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-7567b03adb7c24257dadb1e70012be0b_l3.png» width=»147″ height=»36″>

(так же пишутся и центральные углы, опирающиеся на одну дубугу н.э).

Треугольник AOD — равнобедренный (AO=OD=R), в нем OF=H/2 — высота, медиана и биссектриса.

Треугольный ОФД — прямоугольник. По теореме Пифагора получаем соотношение, связывающее радиус сферы с радиусом и высотой цилиндра, вписанного в сферу:

O{D^2} = O{F^2} + F{D^2}, стрелка вправо » src=»https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2f9164536189bed781a69e072f77a05e_l3.png» width=»179″ height=»21″>

{R^2} = {(frac{H}{2})^2} + {r^2}.» src=»https://www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-31c1b9973089ea02c4bc8e2137def658_l3.png» width=»129″ height=»37″>

Это же соотношение можно получить из прямоугольного треугольника ABD: по теореме Пифагора

Контрольная работа № 5«Объем шара и площадь сферы»

Содержание (быстрый переход):

Цель: проверить знания, умения и навыки учащихся по теме.Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

2. Контрольная работа

   1 уровень сложности

Вариант 1

1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π3 см3. Площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.

Вариант 2

1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов шара и цилиндра.

   2 уровень сложности

Вариант 1

1. Медный куб, ребро которого 10 см, переплавлен в шар. Найдите радиус шара.
2. Радиус шара равен R. Определите объем шарового сектора, если дуга в осевом сечении сектора равен 90°.
3. Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найти объем стенок.

Вариант 2

1. Свинцовый шар, диаметр которого 20 см, переплавлен в шарики с диаметром в 10 раз меньше. Сколько таких шариков получилось?
2. Радиус шара равен R. Определите объем шарового сектора, если дуга в его осевом сечении равна 60°.
3. Поверхность шара равна 225π м2. Определите его объем.

   3 уровень сложности

Вариант 1

1. Объем шара 400 см3. На радиусе как на диаметре построен другой шар. Найдите объем малого шара.
2. Площадь поверхности куба равна площади поверхности шара. Найдите отношение объемов куба и шара.
3. Диагональным сечением прямоугольного параллелепипеда, вписанного в шар, является квадрат площадью S. Найдите объем шара.
4. Диаметр шара радиуса 12 см разделен на 3 части, длины которых относятся как 1 : 3 : 4. Через точки деления проведены плоскости, перпендикулярные диаметру. Найдите объем образовавшегося шарового слоя.

Вариант 2

1. Объем шара равен 15 см3. На диаметре как на радиусе построен другой шар. Найдите объем большего шара.
2. Площадь поверхности прямоугольного параллелепипеда равна площади поверхности шара. Найдите отношение объемов параллелепипеда и шара, если ребра параллелепипеда, исходящие из одной вершины относятся как 1 : 2 : 4.
3. Диагональным сечением прямоугольного параллелепипеда, вписанного в шар, является квадрат. Найдите площадь этого диагонального сечения, если объем шара равен V.
4. Диаметр шара радиуса 9 см разделен на 3 части, длины которых относятся как 1 : 2 : 3. Через точки деления проведены плоскости, перпендикулярные диаметру. Найдите объем шарового слоя.

3. Рефлексия учебной деятельности (ОТВЕТЫ)

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.Домашнее задание: решить задачи, с которыми ученик не справился.

   Ответы на 3 уровень сложности

Вы смотрели: Геометрия 11 класс Контрольная № 5. Поурочное планирование по геометрии для 11 класса. УМК Атанасян (Просвещение). Урок 53. Контрольная работа по геометрии «Объем шара и площадь сферы» + ОТВЕТЫ.

Смотреть Список всех контрольных по геометрии в 11 классе по УМК Атанасян.

В цилиндр, вписанный в шар, вписан шар. Найдите отношение площадей поверхностей и объемов этих шаров.

24.
В треугольнике известна сторона а и
прилежащие к ней два острых угла, которые
равны
и.
Этот треугольник вращается вокруг
прямой, которая лежит в плоскости
треугольника и проходит через вершину
третьего угла перпендикулярно к его
биссектрисе. Определите объем тела
вращения.

25.
В треугольнике известны сторона с и два
прилежащих острых угла, которые равны
и.
Этот треугольник вращается около прямой,
которая проходит через вершину третьего
угла параллельно известной стороне.
Определите объем тела вращения.

26.
В конус вписана правильная шестиугольная
пирамида с высотой 4 см и плоским углом
при вершине
.
Найдите полную поверхность конуса.

Объем сферы: формула и примеры

Давайте научимся определять объем сферы .

Что такое сфера?

Сфера — это идеально симметричная трехмерная форма, все точки поверхности которой равноудалены от центра . Расстояние от центра до любой точки поверхности называется радиусом . Удвоенный радиус равен диаметру или отрезку, проходящему через центр. Примерами сферических объектов являются шарики, пузыри и шарики.

Как найти объем сферы

объем сферы составляет четыре трети произведения пи и радиуса в кубе, как выражено в этой формуле: 

V = (4/3 ) π r 3 где π  = 3,14 и r = радиус

Как и другие трехмерные фигуры, объем сферы измеряется в кубических единицах, таких как кубический дюйм (в 2 3 ) , кубические футы (футы 3 ), кубические сантиметры (см 3 ), или кубический метр (м 3 ).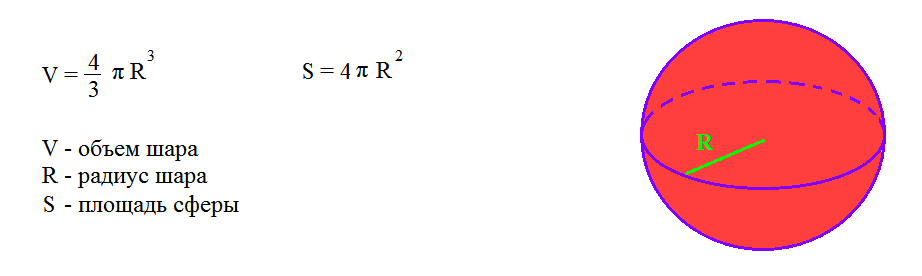

Вот краткое руководство по нахождению объема сферы:

Шаг 1. Запишите данные числа. Вам понадобится радиус или диаметр. Убедитесь, что все единицы измерения одинаковы. Если нет, конвертируйте любой из них.

Шаг 2. Подставьте цифры в формулу.

Шаг 3. Выполнить операции: умножение и деление. Не забудьте указать единицу локтя вместе с ответом.

Дополнительная литература: Объем цилиндра – формула и примеры

Пример 1: Определение объема сферы по заданному радиусу

Найдите объем сферы ниже.

Решение для примера 1:

Запишите данное число, которое является радиусом (r = 3 см) .

Подставьте 3 см вместо r в формулу.

V=(4/3) π r 3

V=(4/3) π (3 см) 3

Упрощение.

V = (4/3) π (27 см 3 )

V = 113,09 см 3 …

Следовательно, Том составляет около 113. 09CM 3 .

Пример 2. Нахождение объема сферы по диаметру

Найдите объем сферы ниже.

Решение для примера 2:

Запишите данную цифру, которая является диаметром (d = 9 см) . Поскольку формула объема сферы требует значения радиуса, найдите радиус.

Вы, наверное, помните, что диаметр в два раза больше радиуса. Итак, разделите диаметр (d = 9см) на 2, чтобы получить радиус.

r = d/2 = 9 см/2 = 4,5 см

Подставьте 4,5 см вместо r в уравнение.

V=(4/3) π r 3

V=(4/3) π (4,5 см) 3

Упростить.

В=(4/3) π (91,125 см 3 )

V = 381,70 см 3 …

Следовательно, объем равен примерно 381,70 см 3 .

Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут какие-либо вопросы о объеме сферы .

Радиус сферы, вписанной в правильную n — угольную пирамиду

Решение. Рассмотрим правильную n — угольную пирамиду SA₁A₂ . A_n и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).

Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

(2)

В силу следствия 2 из формул (1) и (2) получаем

из формулы (3) получаем соотношение

Ответ.

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

Утверждение 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.

Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис. 5).

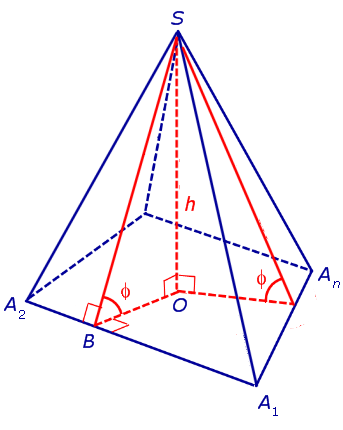
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).

Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

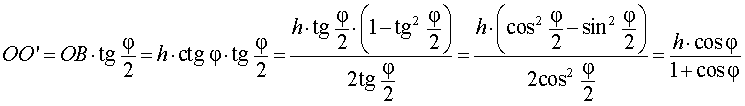
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

(1)

Призма. Прямоугольный параллелепипед

Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.

Правильной призмой называется прямая призма, основание которой — правильный многоугольник.

Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.

Соотношения для прямой призмы

Пусть H — высота прямой призмы, AA₁ — боковое ребро,

V

Особенности правильной шестиугольной призмы

В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.

— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

— Меньшая диагональ правильного шестиугольника в

— Угол между сторонами правильного шестиугольника равен 120°.

— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Пусть вне плоскости многоугольника

Pn

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.

Соотношения для правильной пирамиды

Пусть H — высота правильной пирамиды, h — ее апофема,

V

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

— все вершины сечения лежат на рёбрах многогранника;

— все стороны сечения лежат в гранях многогранника;

— в каждой грани многогранника лежит не более одной стороны сечения.

Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.

Пусть h — высота цилиндра, r — радиус основания, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:

Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.

Пусть h — высота конуса, r — радиус основания, l — образующая, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:

Sphere Calculator

GENERATE WORK

сообщите об этом объявлении

GENERATE WORK

Калькулятор площади поверхности и объема сферы использует длину радиуса сферы и вычисляет площадь поверхности и объем сферы.
Калькулятор сфер — это онлайн-инструмент для геометрии, требующий длины радиуса сферы. С помощью этого калькулятора мы поймем, как найти площадь поверхности и объем сферы.

Необходимо выполнить следующие шаги:

Введите в поле длину радиуса сферы. Значение должно быть положительным вещественным числом или параметром

Обратите внимание, что длина сегмента всегда положительна;
Нажмите кнопку » GENERATE WORK «, чтобы выполнить расчет;
Калькулятор сфер покажет площадь поверхности и объем сферы.

Ввод: Положительное действительное число или параметр в виде длины радиуса сферы; 93\раз\пи$$
где $r$ — длина радиуса сферы и $\pi\приблизительно3.14$.

Множество точек в пространстве, равноудаленных от данной точки $O$, называется сферой. Точка $O$ называется центром сферы.
Расстояние от центра сферы до любой точки сферы называется радиусом этой сферы.
Радиус сферы должен быть положительным действительным числом. Отрезок, соединяющий две точки на сфере и проходящий через центр, называется диаметром шара.
сфера. Все радиусы сферы конгруэнтны друг другу. Сферу можно получить, вращая полукруг вокруг диаметра. Две сферы одного радиуса конгруэнтны.

Любое поперечное сечение сферы плоскостью является окружностью.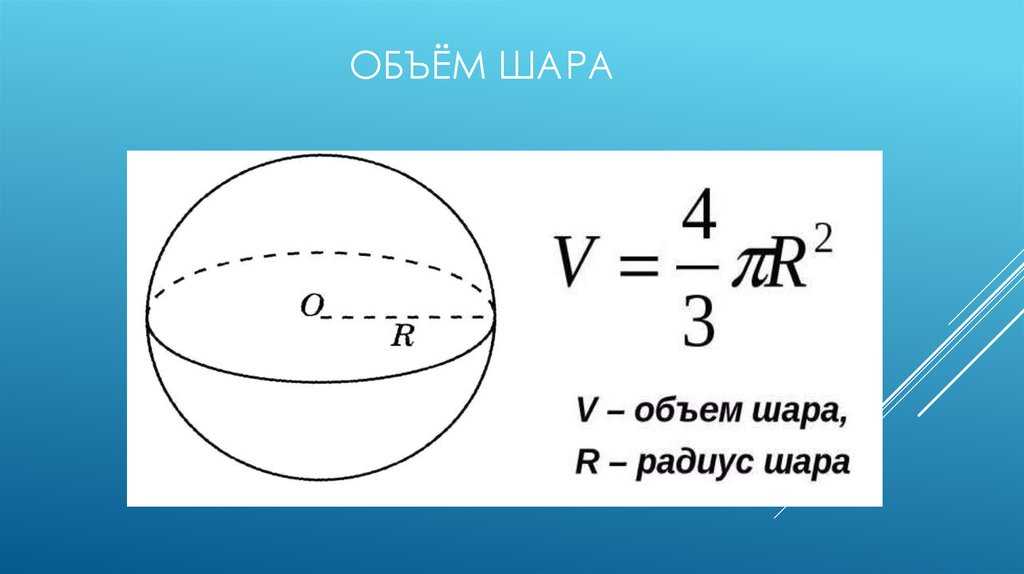

Площадь поверхности и объем сферы с шагами показывает полный пошаговый расчет для нахождения площади поверхности и объема сферы с радиусом $5\;in$ с использованием площади поверхности и формулы объема. Для любого другого значения длины радиуса сферы просто укажите положительное действительное число и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор сфер для выполнения работы, проверки результатов площади поверхности и объема трехмерных тел или эффективного решения домашних задач. Они могут использовать эти методы для определения площади поверхности и объема частей сферы.

Реальные задачи с использованием показателей сферы

Вычисление объема и площади поверхности сферы играет важную роль в математике и в реальной жизни. Формулы для объема и площади поверхности сферы можно использовать для исследования многих других формул и математических уравнений. Полушарие, сферический сегмент, сферический клин, сферический колпачок и сферический сектор являются частями сферы, и формулы их объемов и площадей поверхности выводятся с помощью формул объема и площади поверхности сферы.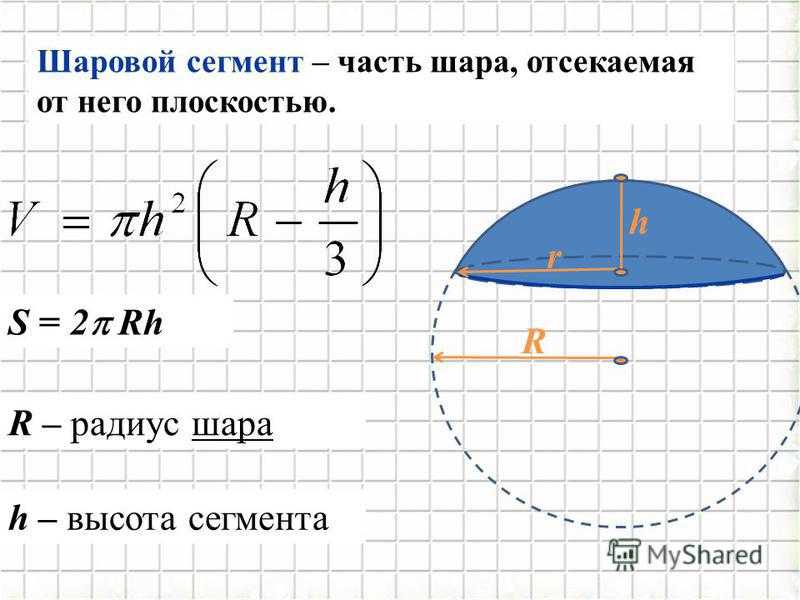

Многие виды спорта, в которых играют с помощью мяча, требуют изучения сферы, а также ее свойств. Например, в футболе чрезвычайно важны площадь поверхности и объем мяча. Различные объемы и площади поверхности мяча могут влиять на скорость удара, траекторию мяча и его раскачивание в воздухе.
Помимо футбола, площадь поверхности и объем сферы важны и во многих других видах спорта. Теннис, гандбол, бейсбол, гольф, баскетбол — все эти виды спорта вращаются вокруг сферических мячей.

Объем и площадь поверхности сферы Практические задачи

Практическая задача 1 : Окружность Земли по экватору составляет $24 903$ миль. Диаметр Луны составляет $2155$ миль. Найди
площадь поверхности Земли и Луны.

Практическая задача 2 : Если баскетбольный мяч имеет диаметр $14$ сантиметров, а теннисный мяч
диаметром $7$ сантиметров, найдите разницу объемов двух шаров.

Калькулятор сферы, формула, пример расчета (работа с шагами) и практические задачи были бы очень полезны учащимся начальной школы K-12 для понимания концепции объема и площади поверхности сферы.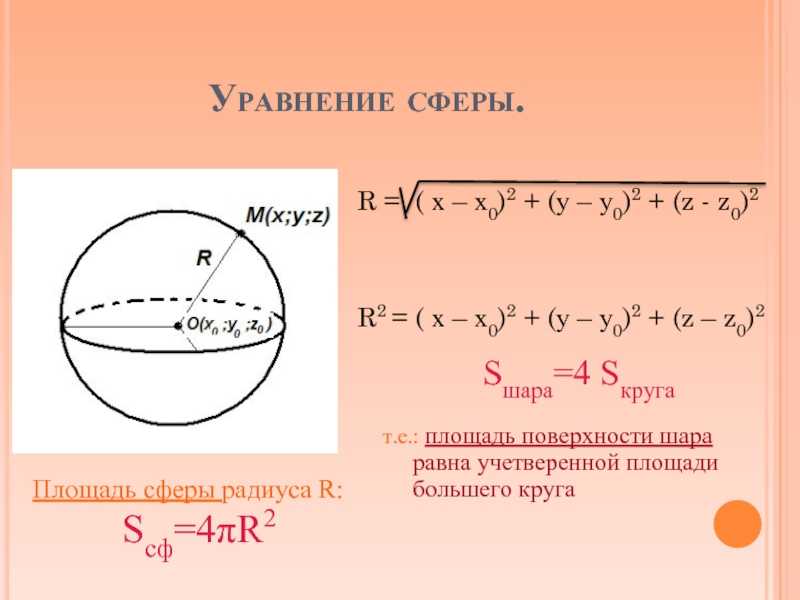

Задача

Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость?

Решение
.

Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.

Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR

Откуда

R = L / 2π

R = 46 / 2π

R = 23 / π

Откуда площадь основания равна

S = πR
2
S = π (23/π) 2

S = 529 / π

Площадь сферы найдем по формуле:

S = 4πr 2

Соответственно площадь полусферы

S = 4πr 2 / 2

S = 2π (23/π) 2

S = 1058 / π

Общая площадь поверхности фигуры равна:

529 / π + 1058 / π = 1587 / π

Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)

1587 / π * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г

Заключение

На уроке мы разо­бра­ли ком­би­на­ции шара, приз­мы,  ци­лин­дра и  пи­ра­ми­ды, а также ре­ши­ли за­да­чи на на­хож­де­ние ра­ди­у­сов впи­сан­но­го и опи­сан­но­го шара.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/11-klass/btela-vraweniya-b/kombinatsiya-shara-i-tsilindra

http://interneturok.ru/ru/school/geometry/11-klass/btela-vraweniya-b/kombinatsiya-shara-i-piramidy

https://www.youtube.com/watch?v=P7_5qWj2BZM

https://www.youtube.com/watch?v=BjtAVlNmtGE

https://www.youtube.com/watch?v=UVukKUD2Sfk

http://nsportal.ru/sites/default/files/2014/09/30/kombinatsii_shara_s_.doc

http://cs7004.vk.me/c7006/v7006056/118db/6ebr4S1_lWc.jpg

http://cs14112.vk.me/c7006/v7006056/118fb/e2bNgVRz0ac.jpg

http://ppt4web.ru/images/111/7601/640/img3.jpg

http://5klass.net/datas/geometrija/Zadachi-po-geometrii-11-klass/0013-013-Izmerenija-prjamougolnogo-parallelepipeda.jpg

http://takya.ru/download/dlya-togo-chtobi-okolo-piramidi-mojno-bilo-opisate-sferu-neobh.doc

http://fs.nashaucheba.ru/tw_files2/urls_3/1132/d-1131348/img8.jpg

Призма вписана в шар

http://festival.1september.ru/articles/633696/presentation/pril.ppt