Калькулятор площади эллипса

Практика

Качаем, запускаем. Видим такое окно:

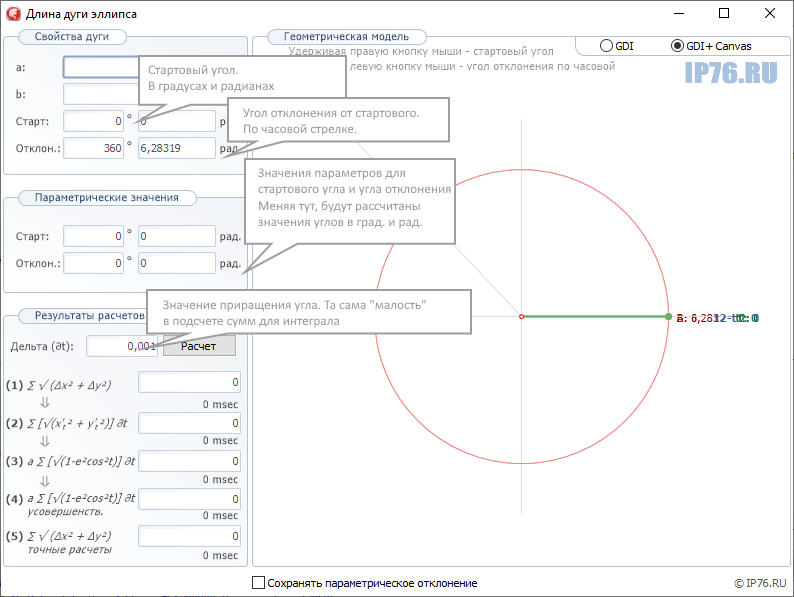Рис.3. Пример: Вид при запуске

При запуске в полях полуосей находятся «земные» значения. Эллипс сильно смахивает на окружность. Можно сразу нажать «Расчет», увидеть значения полярного меридиана, и начинать уже эксперименты.

Для начала проверим корректность получаемых результатов. Я попытался найти какие-нибудь онлайн калькуляторы для подсчета длины дуги эллипса, в которых можно было бы указать стартовый угол и произвольное отклонение, либо просто пару углов, определяющих дугу. Но все калькуляторы считают периметр эллипса. А с произвольной дугой как-то… не встретились.

Картинка из вики:

Заскриним несколько моментов и посчитаем корректность:

Рис.4. Скрины расчетов

Введем a=2, b=0.5, стартовый угол равен 0, отклонение θ=5.642.

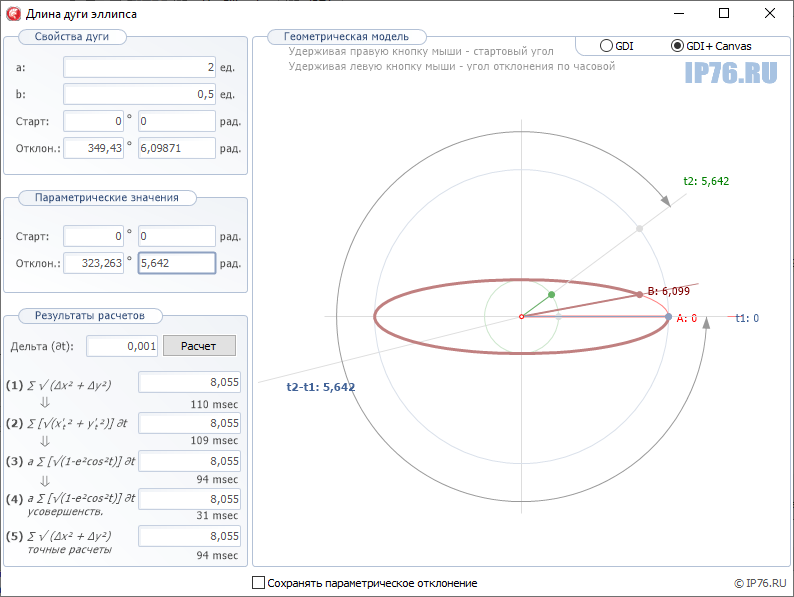Рис.5. Подсчет длины дуги для a=2, b=0.5, стартовый угол=0, отклонение θ=5.642

Видим результат у всех один 8.055. Т.е правы все.

Аналогично поступаем с остальными тремя скринами:

отклонение θ=1.154. У нас получился результат 1.333. На скрине видим результат s=1.334. Как так? Давайте увеличим «Дельту» в 10 раз, т.е. вместо 0.001, сделаем 0,01. У всех интегральных 2) 3) 4) результат станет 1.334. В то время, как у 1) и 5), т.е. примитивно-неинтегрально-хордовых останется 1.333.

Какой результат более истинный? Смотрите сами. Уменьшение дельты, т.е. угла для подсчетов, ведет к более точному результату. На 0.001 интегральные функции выдали результат как хордовые. При более грубой дельте, интегральные чуть изменились, а хордовые верны своему результату.

Сделаем дельту очень мелкой, равной 0.00001. Результат у всех, кроме первой, тот же, 1.333.

Лично я начинаю верить 5-ой формуле.

• отклонение θ= 206. У нас получился результат 4.322. На скрине результат s= 4.322. Дельта 0.001. Все отлично.
• отклонение θ= 4,488. У нас получился результат 5,989. На скрине результат s= 5,989. Дельта 0.001. Все отлично.

Вывод : Формулы 2-5 работают как надо. Фаворит 5. За меньшее время, т.е. при более «грубой» дельте, находит правильный результат.

Проверим на ужасных эллипсах. Т.е. где эксцентриситет очень близок к единице.

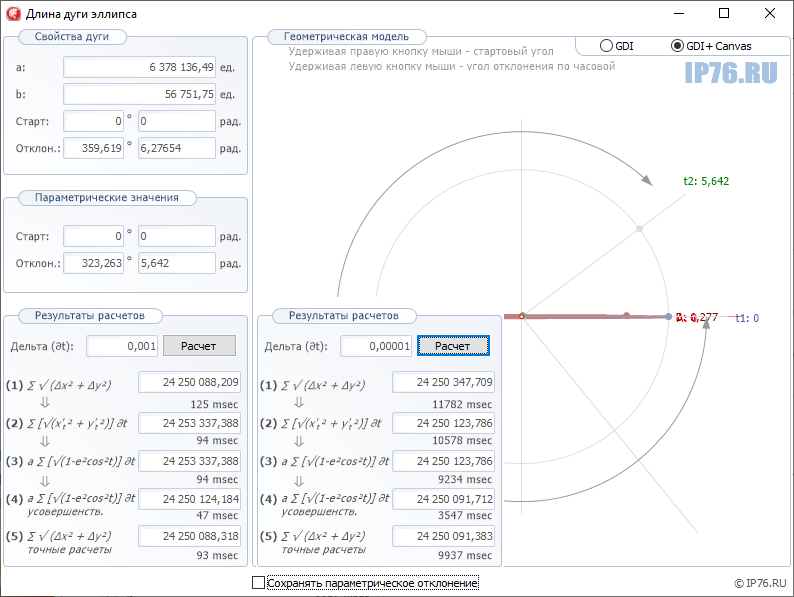Рис.6. Проверка на очень «сплющенном» эллипсе

Можем заметить следующее: при 0.00001 функции 2 и 3 дали результат, близкий к результату функции 4, полученный при дельте 0.001. При дельте 0.00001 функция 4 дала результат, близкий к результату функции 5. Сама же функция 5 слабо колеблется в показаниях, что при дельте в 0.001, что при 0.00001.

Аналогичную ситуацию можно пронаблюдать при сильно вытянутом эллипсе:

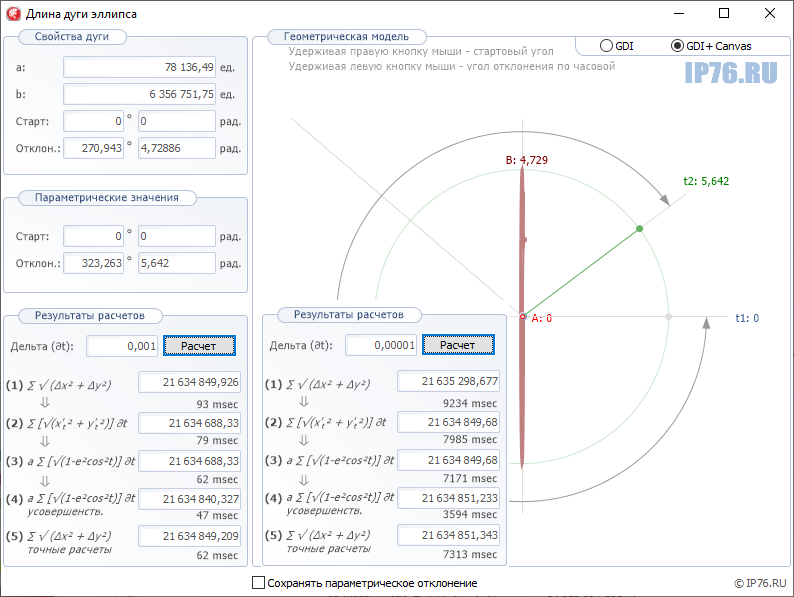Рис.7. Проверка на очень «вытянутом» эллипсе

Таким образом, имеет смысл использовать функции 4 и 5. Одну, как представительницу интегрального сословия, самую быструю и более точную из них. Другую, как представительницу очевидного и простого метода, работающую, между тем, лучше своих интегральных коллег при минимальных ресурсных затратах.

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка

О

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид

aaabOy

Пример 1. Проверить, является ли линия, заданная общим уравнением

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:

Точки

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат – каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:

Эллипс — что это такое, понятие в математике и геометрии

В эллипсе суммарная величина расстояния от любой точки до двух точек F2 и F1 будет равна одному постоянному значению. Эти точки — F1 и F2 — носят названия фокусов эллипса.  

Уравнения эллипса:

Рассмотрим связанные с эллипсом понятия:

1. Отрезок AB, проходящий через фокусы эллипса (его концы должны лежать на эллипсе), носит название большой оси эллипса. Длина этого элемента — большой оси — равняется 2a в уравнении, приведенном выше.
2. Малая ось эллипса — отрезок CD, который перпендикулярен большой оси, он проходит через центральную точку большой оси. Концы отрезка должны лежать на эллипсе.
3. Центр эллипса — точка пересечения малой и большой оси данной замкнутой кривой.
4. Большая полуось — отрезок, проведенный из центра эллипса к вершине большой оси. Обозначается буквой «a».
5. Малая полуось — отрезок, проведенный из центра эллипса к вершине малой оси. Обозначается буквой «b».
6. Фокальные радиусы в точке — расстояния  до определенной точки от каждого фокуса эллипса.
7. Фокальное расстояние — расстояние, равное: 
8. Эксцентриситет — величина, равная: 
9. Диаметр эллипса — свободно проведенная хорда, проходящая через центр построения. Диаметры (обычно пара), обладающие свойством середины хорд, параллельные первому диаметру, и находящиеся на втором диаметре, называются сопряженными диаметрами. Середины хорд, параллельных второму диаметру, находятся на первом диаметре.
10. Радиусом называют отрезок, соединяющий в данной точке центр эллипса и точку. Длина радиуса вычисляется по формуле: . В данной формуле y — величина угла между большой полуосью и радиусом.
11. Фокальный параметр  — половина длины хорды, проходящей через фокус эллипса, является перпендикулярной большой оси.
12. Коэффициент сжатия, или же эллиптичность — отношение длины большой полуоси к длине малой полуоси. Вычисляется по формуле: . Величина, равная , будет носить название «сжатие эллипса». Следует помнить, что для окружности коэффициент сжатия равен единице, а сжатие равно нулю. Эксцентриситет и коэффициент сжатия связаны отношениями равными: .
13. Директриса — прямая, которая существует для каждого фокуса эллипса. При этом соотношение расстояния от свободно расположенной точки эллипса до фокуса этой замкнутой кривой к расстоянию от данной точки до определенной прямой будет равно эксцентриситету эллипса. Полный эллипс находится на той же стороне от такой же прямой, что и его фокус. Уравнения для директрис эллипса в классическом виде пишутся как  для каждого фокуса . Расстояние от фокуса до директрисы будет вычисляться по соотношению 

Теорема директрисы: Для того, чтобы определенная точка находилась на границе линии замкнутой кривой, необходимо, чтобы соотношение расстояния до фокуса к расстоянию до соответствующей директрисы было равно e.

Формула длины окружности эллипса

Хотя рассматриваемая фигура является достаточно простой, длину ее окружности точно можно определить, если вычислить так называемые эллиптические интегралы второго рода. Однако, индусский математик-самоучка Рамануджан еще в начале XX века предложил достаточно простую формулу длины эллипса, которая приближается к результату отмеченных интегралов снизу. То есть рассчитанное по ней значение рассматриваемой величины будет немного меньше, чем реальная длина. Эта формула имеет вид: P ≈ pi * , где pi = 3,14 — число пи.

Например, пусть длины двух полуосей эллипса будут равны a = 10 см и b = 8 см, тогда его длина P = 56,7 см.

Каждый может проверить, что если a = b = R, то есть рассматривается обычная окружность, тогда формула Рамануджана сводится к виду P = 2 * pi * R.

Отметим, что в школьных учебниках часто приводится другая формула: P = pi * (a + b). Она является более простой, но и менее точной. Так, если ее применить для рассмотренного случая, то получим значение P = 56,5 см.

Овал
— это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).

Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА
не имеет верхней границы. В частности R = О 1 О 2
(см. рис. 13.46.а, и рис. 13.46.в), а центры О 3
и О 4
определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.

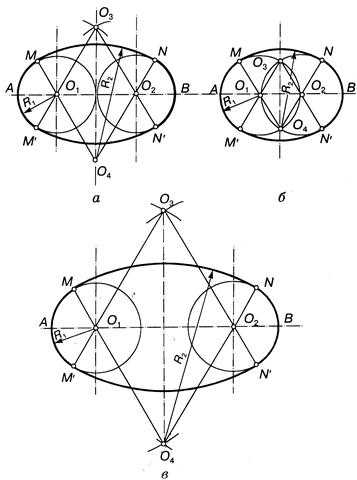
Построение овала с соприкасаю­щимися опорными окружностями
(задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О
и 0 1
радиусом, равным, например, расстоянию между их центрами, проводят дуги окруж­ностей до пересечения в точках О
2 и О 3 .

Рисунок 3.44

Если из точек О
2 и О 3
провести прямые через центры О
и O 1
, то в пересечении с опорными окружнос­тями получим точки сопряжения С
,
C 1
, D
и D 1
. Из точек О
2 и О 3
как из центров радиусом R 2
проводят дуги сопряжения.

Построение овала с пересека­ющимися опорными окружностями
(задача также имеет множество решений) (рис. 3.45). Из точек пе­ресечения опорных окружностей С 2
и О 3
проводят прямые, например, через центры О
и O 1
до пересечения с опорными окружностями в точках сопряжения С, С 1 D
и D 1
, а ра­диусами R 2 ,
равными диаметру опорной окружности,- дуги со­пряжения.

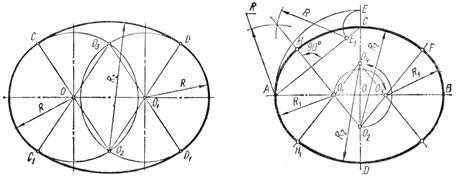
Рисунок 3.45 Рисунок 3.46

Построение овала по двум задан­ным осям АВ и CD
(рис. 3.46). Ниже приведен один из множества вариантов решения. На верти­кальной оси откладываются отре­зок ОЕ,
равный половине большой оси АВ.
Из точки С
как из центра проводят дугу радиусом СЕ
до пе­ресечения с отрезком АС
в точке Е 1
. К середине отрезка АЕ 1
восстанавливают перпендикуляр и отмечают точки его пересечения с осями ова­ла O 1
и 0 2 .
Строят точки O 3
и 0 4
, симметричные точкам O 1
и 0 2
от­носительно осей CD
и АВ.
Точки O 1
и 0 3
будут центрами опорных ок­ружностей радиуса R 1 ,
равного от­резку О 1 А,
а точки O 2
и 0 4 —
цент­рами дуг сопряжения радиуса R 2 ,
равного отрезку О 2 С.
Прямые, со­единяющие центры O 1
и 0 3
с O 2
и 0 4
в пересечении с овалом опреде­лят точки сопряжения.

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

2. пересекаются;

3. не пересекаются.

Рассмотрим первый случай. Строят отрезок OO 1 =2R, параллельный оси Х, на его концах (точки О и О 1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R 1 =2R. Из точек пересечения вспомогательных окружностей О 2 и О 3 строят дуги CD и C 1 D 1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C 1 D 1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

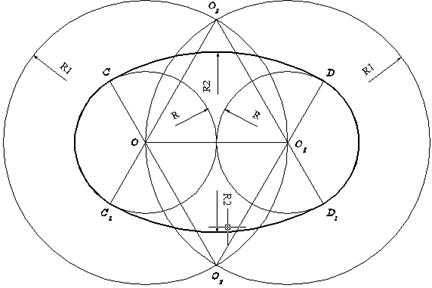
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса

Предлагаем опробовать самый универсальный

Определение слова «периметр».

Слово периметр означает путь, который окружает область. Оно происходит от греческого слова «пери», что означает «вокруг», и «метрон», что означает «мера». Его первое зарегистрированное использование было в 15 веке. В математике периметр относится к общей длине сторон или ребер многоугольника, двумерной фигуры с углами. При описании измерения окружности мы используем слово «окружность», которое представляет собой просто периметр окружности.
Есть много практических приложений для нахождения периметра объекта. Знание того, как найти периметр, полезно для определения длины забора, необходимого для ограждения двора или сада, или количества декоративного бордюра, необходимого для покрытия верхних краев стен комнаты. Кроме того, знание периметра или окружности колеса позволит вам узнать, какое расстояние оно проедет за один оборот.
Перейдите по этой ссылке для получения дополнительной информации.

Периметр квадрата

Для периметра квадрата используйте сторону x 4.
Эту форму легко рассчитать, потому что вам нужно только одно измерение. Это очень простой расчет, который не требует калькулятора. Однако в практических вопросах он используется редко.

Периметр прямоугольника

Формула для определения периметра окружности прямоугольника: (ширина + высота) х 2.
Для прямоугольника нужно измерить его ширину и длину. Вы должны убедиться, что оба измерения находятся в одних и тех же единицах измерения, или преобразовать их по мере необходимости. Из-за своей простоты измерения легко проводить. Калькулятор периметра упрощает расчеты только тогда, когда числа становятся большими.

Окружность круга

Формула для вычисления окружности площади: 2πr. Однако диаметр окружности можно записать как d = 2r. r — радиус, d — диаметр.
Часто легче точно измерить диаметр, чем радиус во многих ситуациях. Во многих инженерных схемах по умолчанию используется диаметр окружности, а не радиус.

Периметр параллелограмма

Формула для определения периметра периметра параллелограмма: (ширина + высота) * 2.
Периметр параллелограмма вычисляется по той же формуле, что и прямоугольник. Это потому, что стороны с обеих сторон равны по длине.

Периметр трапеции

Формула для определения периметра трапеции трапеции:
основание 1 + основание 2 + сторона а + сторона б
Трапеция требует большего количества измерений, потому что это более сложная форма, каждая сторона которой может иметь разную длину.

Периметр сектора

Формула для определения периметра сектора: 2 * радиус + радиус * угол * (π / 360).
Формула для расчета доли сектора в круге идентична, потому что это только одна часть. Сложность возникает с подсчетом того, за сколько кругов отвечает сектор.

Периметр восьмиугольника

Для периметра правильного восьмиугольника сторона * 8 — это формула.
Эту форму проще всего вычислить по периметру. Требуется только одно измерение, и вы можете просто умножить на восемь, чтобы получить результат. В инженерии, ландшафтном дизайне, садоводстве и архитектуре вы можете встретить правильные восьмиугольники.

Универсальные формулы для расчётов параметров овала

Однако, оказывается, вертикальную ось овала на нашем чертеже необязательно делить именно на пять частей. Можно и на четыре части, и на три, и на шесть. Более того, вообще необязательно её делить на равные части. Угол, образованный горизонтальной осевой и линиями AB вообще может быть любым (в пределах чертежа, конечно же).

Обозначим этот угол символом γ. И пусть оси овала (его длина и ширина соответственно) равны a и b.

Тогда универсальные формулы для расчёта параметров овала будет выглядеть так:

R=[(b/2*(sin(γ
)-1)+(a/2*cos γ
)] /

r=[(b/2*cos (γ
/2)) — (a/2*sin (γ
/2))] / [(cos (γ
/2)-sin (γ
/2)]

Выглядят страшновато? Хм, пожалуй, так и есть. Но зато, применяя эти формулы, мы можем свободно задавать три параметра: длину овала, его ширину и вспомогательный угол γ. А это означает, что мы можем рассчитать овал с любыми заданными габаритными размерами a и b, да ещё и не один. С одними и теми же значениями a и b мы можем получить столько разных овалов, сколько сможем придумать различных значений вспомогательного угла γ, вписывающихся в чертёж.

Поясним на примере. Пусть нам нужно рассчитать овал, оси которого равны 150 и 84 см соответственно (параметры большого овала нашей ванны на 500 л). Из таблицы видно, как будут меняться диаметры D и d, длины большой и малой дуг M и m, а также периметр овала p в зависимости от изменения угла γ.

Длина овала, a, см	Ширина овала, b, см		Диаметр большой дуги, D, см	Диаметр малой дуги, d, см	Длина большой дуги, M, см	Длина малой дуги, m, см	Периметр овала, p, см

Все эти овалы будут иметь немного разные контуры, но одни и те же габаритные размеры — 150х84 см.

При этом, задавая значения для большого и малого овалов нашего изделия, мы свободно можем задать одинаковую конусность для большой и малой дуг, что сделает наши овалы как бы равномерно вписанными один в другой, если смотреть на них сверху. У таких изделий разница больших и малых диаметров будет одинакова, а, следовательно, одинаковым будет и коэффициент конусности. Пример такого изделия — наш пуфик , имеющий такие параметры: диаметры больших дуг — 96 и 90 см, диаметры малых дуг — 36 и 30 см, длины большого и малого овалов — 66 и 60 см, а их ширины — 44 и 38 см. Как видите, разница как в диаметрах, так и в габаритных размерах везде равна 6 см. Коэффициент конусности при высоте клёпки в 45 см составляет 0,133. Деревянные обручи по всей поверхности натягиваются на изделие одинаково и надёжно фиксируются на заданной высоте.

Для того, чтобы не нужно было каждый раз проводить сложные расчёты, достаточно один раз забить вышеприведённые формулы в какую-нибудь вычислительную программку. Ниже вы можете скачать документ Excel, в которой вводятся только величины a и b (нужно ввести одинаковые значения во все строки), после чего программа автоматически сгенерирует все необходимые параметры таких овалов при широком спектре угла γ. Только ничего не вводите от руки в другие столбцы, чтобы не заменить формулы числовыми значениями.

В астрономии, когда рассматривают движение космических тел по орбитам, часто применяют понятие «эллипс», поскольку их траектории характеризуются именно этой кривой. Рассмотрим в статье вопрос, что представляет собой отмеченная фигура, а также приведем формулу длины эллипса.

Плюсы и минусы каждого из тренажёров, советы

Одно из самых простых и самых естественных упражнений – это бег.

Он насыщает клетки организма кислородом, заряжает тело энергией и бодростью, способствует снижению веса, повышает общую выносливость человека.

Именно утренняя пробежка у многих горожан ассоциируется со здоровым образом жизни. Но, к сожалению, далеко не все желающие могут себе позволить бегать.

Во-первых, в наших широтах хорошая тёплая погода с утра – это большая редкость.

Во-вторых, многие жители больших городов по утрам встают так рано, что на улице ещё темно, а домой возвращаются тоже после наступления сумерек.

Выходом для тех, кто мечтает заниматься бегом, но не может себе этого позволить, является домашний тренажёр.

Что лучше – беговая дорожка или эллиптический тренажёр?

Если сравнивать два этих приспособления, можно подчеркнуть, что беговая дорожка позволяет получать максимально естественные тренировки с обычной кардионагрузкой.

httpv://www.youtube.com/watch?v=embed/QJDHPCQoQm4

Беговая дорожка: преимущества и недостатки

Главным плюсом беговой дорожки является естественная для человека нагрузка, которая имеет минимальное количество противопоказаний. Из достоинств этого тренажёра можно также назвать:

1. Быстрота сжигания калорий. Один час тренировок на таком тренажёре помогает избавиться от 800 калорий.      
2. Поскольку бег и ходьба заставляют работать все системы опорно-двигательного аппарата, занятия на беговой дорожке благотворно отражаются на состоянии мышц и костей, улучшают осанку, повышают общую выносливость организма.
3. Наличие множества программ помогает сделать тренировки разнообразными, выбрать для себя максимально удобный темп. Новичку на беговой дорожке можно тренироваться не слишком интенсивно, чтобы привыкнуть к ней. А спортсменам с опытом такой тренажёр даёт возможность заниматься с более высокой нагрузкой.

Помимо преимуществ, у беговой дорожки есть также минусы:

• Так же, как и во время уличной пробежки, при занятиях на беговой дорожке суставы получают высокую нагрузку, поэтому у людей, решивших просто начать занятия и не познакомившихся с правилами тренировок на дорожке, через некоторое время могут возникнуть проблемы с опорно-двигательным аппаратом.
• Беговая дорожка – это агрегат с большими габаритами, поэтому владельцам небольшой квартиры от такого тренажёра придётся отказаться.
• Цены на современные дорожки далеко не демократичны.

Плюсы и минусы эллиптического тренажёра

По своей сути данный тренажёр является сложным механизмом с рукоятками для рук и платформами для ног. Тренировки на этом тренажёре – это что-то среднее между ходьбой на лыжах и бегом. По сравнению с беговой дорожкой, эллипсоид имеет целый ряд преимуществ:

1. Нагрузка равномерно распределяется по всем мышечным системам тела, что позволяет сделать её более эффективной.
2. Эллиптический тренажёр является прекрасной альтернативой не только беговой дорожке, но и велотренажёру, и степперу.
3. Благодаря тому, что стопы во время занятий на эллипсоиде не отрываются от платформ, вероятность получить травму колена или голеностопа при тренировке на таком тренажёре гораздо ниже, чем при занятиях бегом на спортплощадке.
4. Габариты эллиптического тренажёра меньше, его проще расположить в небольшой квартире.

httpv://www.youtube.com/watch?v=embed/23m2fliaG5M

Если говорить о минусах эллипсоида, но они тоже есть. В первую очередь к ним можно отнести невозможность регулирования нагрузки. Если беговая дорожка – это тренажёр и для новичков, и для опытных любителей бега, то нагрузка, которую даёт эллипсоид, может оказаться слабоватой для тех, кто тренируется уже не первый месяц.

К недостаткам эллиптического тренажёра также можно отнести:

• Отсутствие «эффекта опоры». Такой эффект является естественным и необходим для тренировки мелких косточек и суставов стопы.
• Неровный темп, невозможность задавать нагрузке высокие темпы. За час тренировки на эллипсоиде можно сжечь не более 700 калорий. Контролировать интенсивность занятий на данном тренажёре сложно, поэтому похудеть с его помощью быстрее не получится: снижение веса будет плавным.

Если говорить о том, что выбрать – эллипсоидный тренажёр или беговую дорожку, следует учитывать уровень своей спортивной подготовки и желаемый результат.

Любителям утренних пробежек, уставших от капризов погоды, домашняя беговая дорожка однозначно понравится и принесёт немало пользы. Тем же, кто не имеет особенного спортивного опыта, хочет улучшить фигуру и общее самочувствие без риска получения травмы, лучше будет приобрести эллиптический тренажёр.

Современные эллиптические тренажеры

Орбитрек — это современный тренажер, также известный как кросс-тренажер. Он сочетает в себе преимущества степпера, велотренажера и беговой дорожки. К тому же он не занимает много места и на нем можно заниматься дома.

В современных моделях имеется дисплей, который показывает:

• пройденный путь;
• время;
• скорость;
• пульс;
• сожженные калории.

Сегодня на рынке представлено множество тренажеров с различными функциями.
Прежде чем приступить к тренировкам на эллипс тренажере, стоит ознакомиться с инструкцией по эксплуатации устройства.

Некоторые эллипсоиды имеют функцию измерения количества жира в организме и даже возможность проведения фитнес-теста. Это позволит, например, правильно подобрать упражнения согласно текущей физической форме.

Многофокусные эллипсы

N-эллипс — это обобщение эллипса, имеющего более двух фокусов. N-эллипсы также называют мультифокальными эллипсами, полиэллипсами, k-эллипсами, эллипсами Чирнхауза. Впервые такие фигуры были изучены Джеймсом Максвеллом в 1846 году.

Пусть на плоскости заданы n точек (ui, vi) (фокусов), тогда n-эллипс есть геометрическое место точек на плоскости, где сумма расстояний до n фокусов есть постоянная величина d формула, это предложение записывается как

1-эллипс — это окружность, 2-эллипс — это правильный эллипс. Обе эти кривые являются алгебраическими кривыми степени 2.

Для любого числа n фокусов n-эллипс представляет собой замкнутую выпуклую кривую. Кривая плавная за пределами зоны фокусировки.

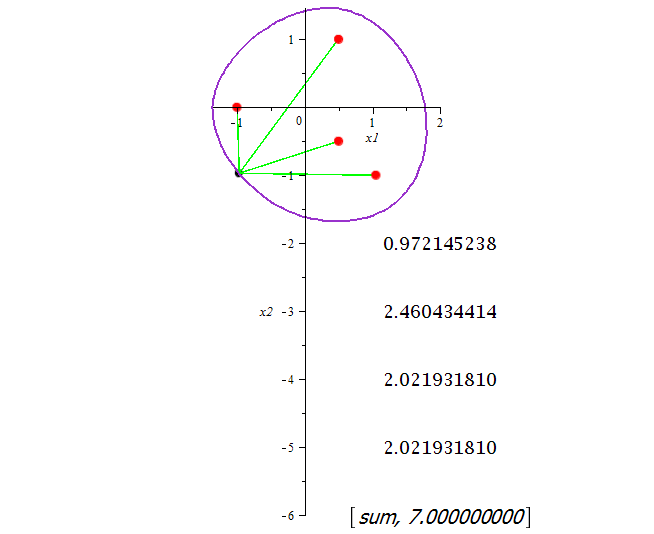
Эллипс с 4 фокусами и фокусным расстоянием d = 7 Эллипс с 4 фокусами и фокусным расстоянием d = 7

Длина дуги через эксцентриситет с подготовкой

Возьмем за основу последнюю функцию. Алгоритм построен так, что в цикле идем от стартового угла, к конечному, на каждой итерации подсчитывая параметр. А если сразу посчитать начальный и конечный параметры и определить условие выхода из цикла? Этим мы однозначно снизим вычислительную нагрузку внутри цикла.

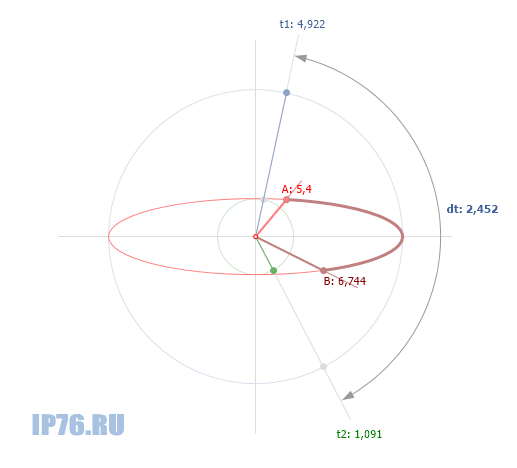Рис.2. Параметры дуги эллипса.

То есть, вместо того, чтобы идти из точки A в точку B, мы заранее считаем параметры t1 и t2. И в цикле больше нахождением параметров не занимаемся, а только считаем очередное приращение.

Берем код последней реализации и улучшаем:

Результат — 40 007 859,543 за 30 милисекунд! Мысль явно здравая.

калькулятора периметра эллипса онлайн

Когда мы имеем дело с круглыми кадками, всё довольно-таки просто. Действительно, есть диаметры — верхний и нижний, есть высота клёпки, нетрудно посчитать периметр… Остаётся только изготовить шаблон и строгать себе, набирая необходимую суммарную ширину клёпок. А как быть, если наше изделие — овальное? Сколько нужно для его изготовления шаблонов, и каких? Как формируется эта плавная линия, переходящая от малых радиусов в торцах изделия к большим, имеющим сравнительно незначительный изгиб, бокам?

Чтобы разобраться в этом вопросе, давайте начнём с метода, описанного Г. Я. Федотовым в книге «Секреты бондарного ремесла» .
Вот что предлагает нам автор в главе «Анкерок», посвящённой изготовлению этого переносного плоского бочонка, имеющего в сечении овал.

Калькулятор окружности эллипса

Калькулятор окружности эллипса поможет вам найти общий периметр вокруг эллипса, который также называется окружностью эллипса. Длина окружности эллипса зависит от длин большой и малой полуосей. Читайте дальше, чтобы узнать больше о том, как найти длину окружности эллипса и формулу для ее расчета.

Что такое длина окружности эллипса?

длина окружности эллипса это общая длина граница эллиптической формы . Другими словами, мы также называем периметр эллипса его окружностью .

Какова формула длины окружности эллипса?

Чтобы вычислить длину окружности эллипса, нам нужно знать длины большой и малой полуосей . Получив их, мы найдем длину окружности эллипса по следующей формуле:

p≈π(a+b)(1+3h20+4−3h)\small
p \ приблизительно \pi (a+b) \left ( 1 + \frac {3h}{10 + \sqrt{4-3h}} \right )p≈π(a+b)(1+10+4−3h 92}h=(a+b)2(a−b)2​

Таким образом, используя приведенные выше уравнения для длины окружности эллипса, мы можем найти ее приблизительное значение.

Как пользоваться калькулятором длины окружности эллипса?

Чтобы найти длину окружности эллипса с помощью нашего калькулятора, необходимо сделать следующее:

1. Введите значение большой полуоси (а) .
2. Введите значение малой полуоси (b) .
3. Вуаля! Инструмент выполнит все тяжелые вычисления для расчета окружность эллипса и отобразит его как результат!

Окружности и эллипсы Знаете ли вы, что эллипс с равными большой и малой осями — это окружность. Узнайте больше о кругах, используя наши специальные инструменты для расчета уравнения круга, калькулятора единичного круга и калькулятора площади круга.

Другие калькуляторы эллипса

Если вы нашли этот инструмент полезным, вы также можете проверить наш широкий выбор калькуляторов, связанных с эллипсом:

• Калькулятор эллипса;
• Калькулятор площади эллипса;
• Вычислитель центра эллипса;
• Калькулятор периметра Эллипса; и
• Вычислитель фокусов эллипса.

Как найти длину окружности эллипса?

Чтобы найти длину окружности эллипса, нам нужно использовать уравнение длины окружности эллипса, которое состоит из следующих шагов:

1. Найдите значения большой полуоси (a) и малой полуоси (б) .
2. Вычислить значение переменной h по формуле .
3. Подставьте значения a, b и h в формулу длины окружности, полученную с помощью следующего уравнения: .
4. Тада! Теперь у вас есть приблизительное значение длины окружности эллипса !

Есть ли у эллипса длина окружности?

Да! Мы иногда называем границу эллипса окружностью эллипса ! Хотя термин окружность обычно ассоциируется с окружностью, мы также используем его для обозначения периметра эллипса.

Дополнительные функции калькулятора

Калькулятор длины окружности овала предоставляет несколько дополнительных функций, которые помогут вам сделать более точные и удобные расчеты:

1. Выбор системы измерения: калькулятор позволяет выбрать измерительные единицы — метры, сантиметры, миллиметры, футы, дюймы. Это позволяет работать в той системе, которая наиболее удобна для ваших нужд.
2. Учет десятичных знаков: калькулятор позволяет указывать количество десятичных знаков, с которыми вы хотите производить расчеты. Это позволяет получить более точные результаты в зависимости от требуемой точности.
3. История расчетов: калькулятор сохраняет историю ваших предыдущих расчетов, что позволяет вам легко отслеживать и сравнивать результаты. Вы можете вернуться к любому предыдущему расчету, чтобы внести изменения или повторить операцию.
4. Подробные инструкции: калькулятор предоставляет подробные инструкции о том, как использовать каждую функцию и как правильно заполнять поля для расчета. Это поможет вам избежать ошибок и получить точные результаты.

Все эти дополнительные функции делают калькулятор длины окружности овала гибким инструментом, который может быть полезным для различных задач и требований. Он позволяет с легкостью производить расчеты, сохранять и анализировать результаты, а также настраивать его в соответствии с вашими предпочтениями и потребностями.

Длина дуги, как сумма хорд

Самое простое, что может прийти в голову, это двигаться от начала дуги к ее концу с небольшим наращиванием угла отклонения, считать хорду и прибавлять ее к накапливаемой сумме.

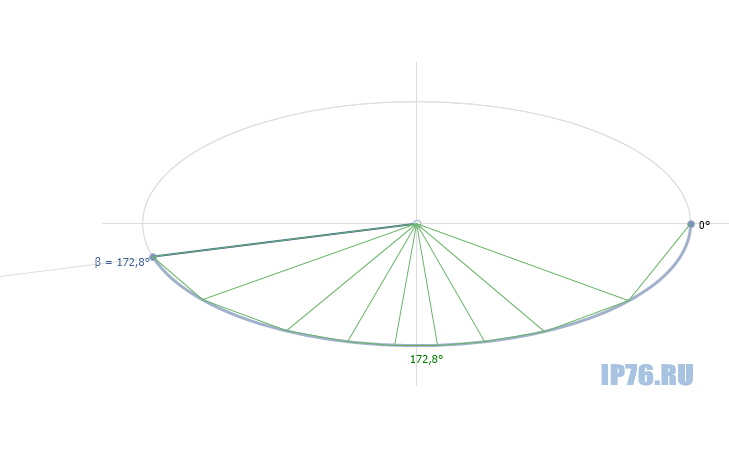Рис.1. Сумма хорд

Формула такова:

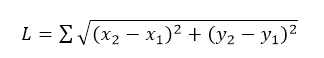(1) Сумма хорд

Проще говоря, находим координаты двух точек на эллипсе, отстоящих друг от друга на некий малый угол, по ним находим хорду, как гипотенузу получившегося прямоугольного треугольника.

В коде выглядит так:

//*****************************************************************
// Нахождение длины дуги эллипса, заданного прямоугольником ARect
// По аналогии с GDI+, углы в градусах, по часовой. Хордами
// ∑ √ (Δx² + Δy²)
//*****************************************************************
function CalcArcEllipseLen1(ARect : TxRect; // эллипс
startAngle : Extended; // старт.угол
sweepAngle : Extended; // угол дуги
deltaAngle : Extended=0.01 // дискрета
): Extended;
var tmp : Extended; // наращиваемый угол
pnt : TxPoint; // новые координаты по tmp
val : TxPoint; // координаты в предыдущей итерации
dw : Extended; // убывающий параметр цикла
l : extended; // длина текущей хорды
begin
// переводим градусы в радианы
startAngle := startAngle * pi/180;
sweepAngle := sweepAngle * pi/180;
deltaAngle := deltaAngle * pi/180;
// инициализируем
tmp := startAngle;
dw := sweepAngle;
result := 0;
// стартовая координата
val := CalcEllipsePointCoord(ARect,tmp);
repeat
// уменьшаем параметр цикла
dw := dw — deltaAngle;
// определяем значение угла
if dw < 0 then tmp := tmp + (deltaAngle+dw)
else tmp := tmp + deltaAngle;
// считаем новую точку на эллипсе
pnt := CalcEllipsePointCoord(ARect,tmp);
// длина хорды
l := sqrt(sqr(val.X-pnt.x)+sqr(val.Y-pnt.y));
// сумма, интеграл
result := result+l;
val := pnt;
until dw < 0;
end;

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

//***************************************************************** //  Нахождение длины дуги эллипса, заданного прямоугольником ARect //  По аналогии с GDI+, углы в градусах, по часовой. Хордами //  ∑ √ (Δx² + Δy²) //***************************************************************** functionCalcArcEllipseLen1(ARectTxRect;// эллипс startAngleExtended;// старт.угол sweepAngleExtended;// угол дуги deltaAngleExtended=0.01// дискрета   )Extended; vartmpExtended;// наращиваемый угол pntTxPoint;// новые координаты по tmp valTxPoint;// координаты в предыдущей итерации dwExtended;// убывающий параметр цикла lextended;// длина текущей хорды begin // переводим градусы в радианы startAngle=startAngle*pi180; sweepAngle=sweepAngle*pi180; deltaAngle=deltaAngle*pi180; // инициализируем tmp=startAngle; dw=sweepAngle; result=; // стартовая координата val=CalcEllipsePointCoord(ARect,tmp); repeat // уменьшаем параметр цикла dw=dw-deltaAngle; // определяем значение угла ifdw<thentmp=tmp+(deltaAngle+dw) elsetmp=tmp+deltaAngle; // считаем новую точку на эллипсе pnt=CalcEllipsePointCoord(ARect,tmp); // длина хорды l=sqrt(sqr(val.X-pnt.x)+sqr(val.Y-pnt.y)); // сумма, интеграл result=result+l; val=pnt; untildw<; end;

Проверим с планетарным размахом. По последним данным Международной Службы Вращения Земли (IERS — 1996) большая экваториальная полуось Земли равна 6 378 136,49 м, а полярная малая — 6 356 751,75 м.

Посчитаем периметр меридиана каким-нибудь онлайн-калькулятором, получаем 40 007 859.543 (некоторые могут дать другое число, т.к. используют приближенные формулы для вычисления периметра).

Представленная выше функция за 109 милисекунд выдала результат 40 007 996.265 при дельте 0.001. Это нельзя назвать точным результатом.