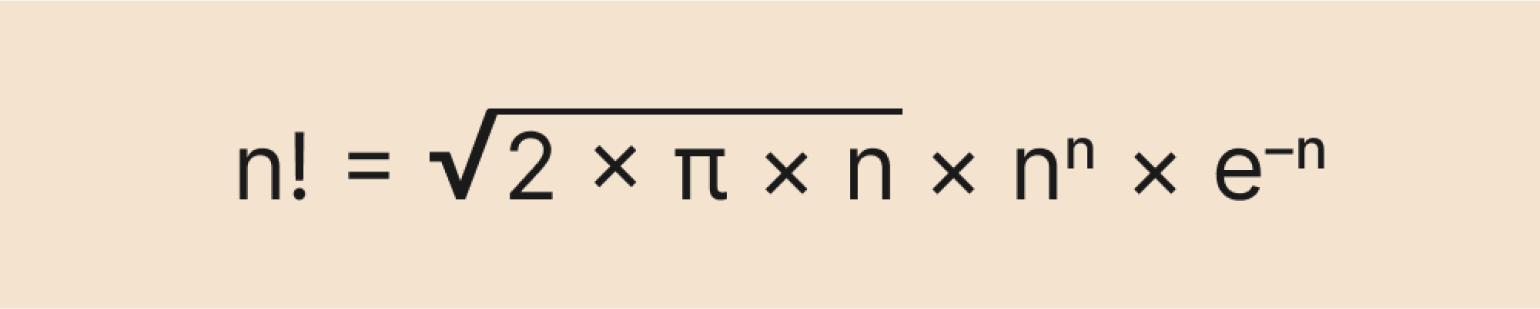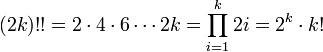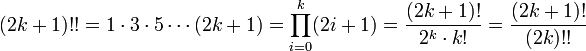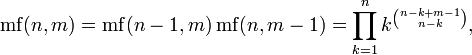Как пишется факториал в математике

Свойства факториала

Рекуррентная формула

Так как факториал — это произведение всех натуральных чисел от до включительно, то можно вывести рекуррентную формулу.

Для примера возьмём :

Можно сгруппировать и представить в виде:

Или так:

Поэтому факториал может быть задан следующей рекуррентной формулой:

n	n!
n = 1	n! = 1
n > 1	n! = (n — 1)! * n

Как следствие:

Комбинаторная интерпретация

В комбинаторике факториал натурального числа интерпретируется как количество перестановок (упорядочиваний) множества из элементов.

Один элемент можно упорядочить одним способом. Два элемента — множество (A,B) — двумя перестановками:

AB
AB	BA

Например, для множества (A,B,C,D) из 4-х элементов существует перестановки:

ABCD
ABCD	BACD	CABD	DABC
ABDC	BADC	CADB	DACB
ACBD	BCAD	CBAD	DBAC
ACDB	BCDA	CBDA	DBCA
ADBC	BDAC	CDAB	DCAB
ADCB	BDCA	CDBA	DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества , т.к. пустое множество упорядочено единственным способом.

Остальные свойства и способы применения факториала в данной статье не рассматриваются.

История

Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение \displaystyle{ n! } предложил французский математик Кристиан Крамп только в 1808 году. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента \displaystyle{ \sqrt{2\pi} } была неопределённая константа).

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:

\displaystyle{ \left({1 \over 2}\right)!=\frac{\sqrt{\pi}}{2} }

Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение:

\displaystyle{ x! = \lim_{m\to\infty} \frac{m^x m!} {(x+1)(x+2)\dots (x+m)} }

Развивая эту идею, Эйлер в следующем, 1730 году, ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Петербургской академии наук в 1729—1730 годах.

Definition of a Factorial

The factorial of a number is the multiplication of all the numbers between 1 and the number itself. It is written like this: . So the factorial of 2 is (= 1 × 2).

To calculate a factorial you need to know two things:

The factorial of 0 has value of 1, and the factorial of a number is equal to the multiplication between the number and the factorial of .

For example, is equal to .

Here the first few factorial values to give you an idea of how this works:

Factorial	Multiplication	Result
0!	1	1
1!	1	1
2!	1 × 2	2
3!	1 × 2 × 3	6
4!	1 × 2 × 3 × 4	24
5!	1 × 2 × 3 × 4 × 5	120
6!	1 × 2 × 3 × 4 × 5 × 6	720
7!	1 × 2 × 3 × 4 × 5 × 6 × 7	5040
8!	1 × 2 × 3 × 4 × 5 × 6 × 7 × 8	40,320
9!	1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9	362,880

analogical dictionary

Факториал (n.)

произведение

фабричный

Wikipedia

Факториал

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

Например:

По определению полагают . Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, … (последовательность A000142 в OEIS)

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

  Свойства

  Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

 
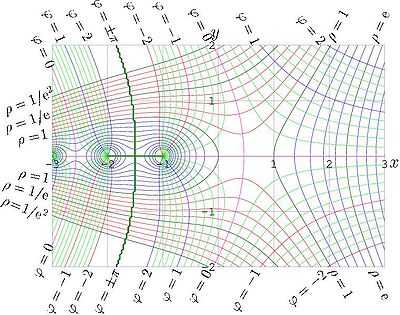
Амплитуда и фаза факториала комплексного аргумента.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

  Формула Стирлинга

Основная статья: Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

  Разложение на простые числа

Каждое простое число p входит в разложение на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Для натурального числа n

  Обобщения

  Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают .

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, … (последовательность A006882 в OEIS)

  Кратный факториал

m-кратный факториал числа n обозначается и определяется следующим образом:

Пусть число n представимо в виде , где , . Тогда

Двойной факториал является частным случаем m-кратного факториала для m = 2.

  Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

Возрастающим факториалом называется выражение

  Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n#  и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов (включая ) начинается так:

, , , , , , 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

  Суперфакториалы

Основная статья: Большие числа

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал числа n как произведение первых n (m-1)-уровневых факториалов, то есть

где для и .

  Субфакториал

Основная статья: Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

1. «Энциклопедия для детей» Аванта+. Математика

   Advertizing ▼

Примечания

Смотреть что такое «Факториал» в других словарях:

ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка

ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь

ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия

факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь

ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия

факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь

факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas

How to Calculate a Factorial Programmatically with JavaScript

There are two ways to calculate factorials programmatically in JavaScript:

How to calculate a factorial in JS with recursion

Let’s get back to the two things to know when calculating a factorial – that is and . We can use the first one to create the base case of the recursive function, because in that case we know the result already.

The second thing to know about how to calculate a factorial, , can be the recursive case.

How to calculate a factorial with a JavaScript loop

We said before that . So, to calculate the factorial of a number with a loop, we can initialize a variable to , and multiply the numbers from to by the variable inside the loop.

In this way, if the input is higher than 1, the output will easily be 1.

Факториал

Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».

Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:

-3,75! 2,23! -2!

Число должно быть целое и положительное:

3! 56! 12!

Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.

• 3! = 1*2*3 = 6
• 4! = 1*2*3*4 = 24
• 5! = 1*2*3*4*5 = 120
• 6! = 1*2*3*4*5*6 = 720

Мы видим, что 4! — это 3!*4 5! — это 4!*5 6! — это 5!*6

Формулы и свойства факториала

Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.

1! = 1

2! = 2

3! = 6

4! = 24

5! = 120

6! = 720

7! = 5040

8! = 40320

9! = 362880

10! = 3628800

11! = 39916800

12! = 479001600

13! = 6227020800

14! = 87178291200

15! = 1307674368000

16! = 20922789888000

17! = 355687428096000

18! = 6402373705728000

19! = 121645100408832000

20! = 2432902008176640000

21! = 51090942171709440000

22! = 1124000727777607680000

23! = 25852016738884976640000

24! = 620448401733239439360000

25! = 15511210043330985984000000

Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:

• (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
• n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
• (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)

С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.

Такая формула дает результат с небольшой погрешностью.

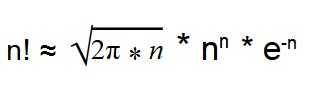Рекуррентная формула

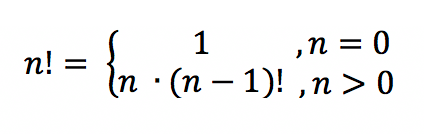• 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
• 6! = 6*(6-1)! = 6*5! = 6*120 = 720

Для решения примеров обращайтесь к таблице.

Примеры умножения факториалов:

1. Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
2. Или раскладывайте факториалы отдельно, если хотите потренироваться: 5! = 1*2*3*4*5 = 4! * 5 =120 7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040 120 * 5040 = 604800

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Примеры решений

Давайте поупражняемся и решим пару примеров.

1. Сократите дробь:

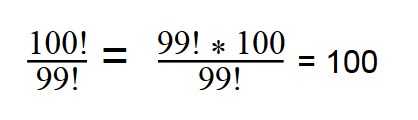
При сокращении факториалов, пользуйтесь свойством: n! = (n — 1)! * n 100! = 99! * 100

Далее сокращаем по принципу сокращения обыкновенных дробей.

2. Вычислите значение выражения с факториалом: 8! + 5!

Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.

А можно потренироваться и разложить их:

8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320 5! = 1*2*3*4*5 = 4!*5 = 120 40320 + 120 = 40440 8! + 5! = 40440

3. Вычислите значение выражения:

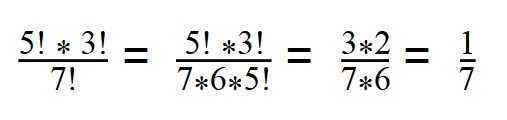
7! = 1*2*3*4*5*6*7 = 5! * 6 *7

Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.

4. Вычислите значение выражение:

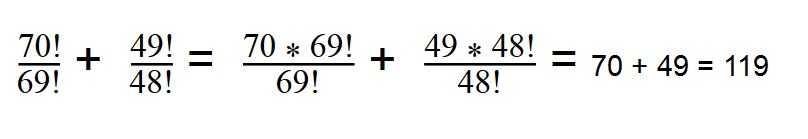
Вы уже знаете, как найти факториал — раскладываем 70 и 49: 70! = 1*2*3*. *69 = 69! * 70 49! = 1*2*3*. 49! * 48

Далее сокращаем все одинаковые множители.

5. Сократите дробь:

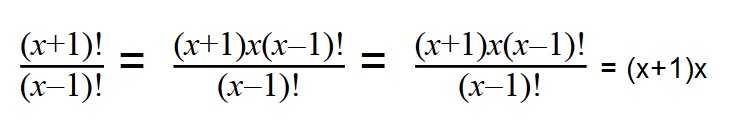
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.

Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.

Свойства

Рекуррентная формула

Факториал может быть задан следующей рекуррентной формулой:

\displaystyle{ n!= \begin{cases}
1 & n = 0,\\
n \cdot (n-1)! & n \gt 0.
\end{cases} }

Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов.

Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения \displaystyle{ 0!=1 } — количество перестановок пустого множества равно единице. Кроме того, формула для числа размещений из \displaystyle{ n } элементов по \displaystyle{ m }

\displaystyle{ A_n^m = \frac{n!}{(n-m)!} }

при \displaystyle{ n=m } обращается в формулу для числа перестановок из \displaystyle{ n } элементов (порядка \displaystyle{ n }), которое равно \displaystyle{ n! }.

Связь с гамма-функцией

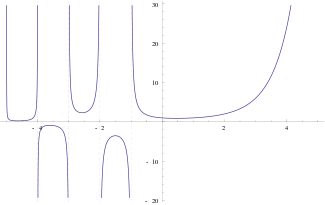
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

\displaystyle{ n! = \Gamma(n+1) }.

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при \displaystyle{ n=-1, -2, -3\ldots }.

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция \displaystyle{ \Pi(z) = \Gamma(z+1) }, которая при \displaystyle{ \mathrm{Re}(z)\gt -1 } может быть определена как

\displaystyle{ \Pi(z)=\int_0^\infty t^{z} e^{-t}\, \mathrm{d}t } (интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: \displaystyle{ \Pi(n) = n! }. Как и факториал, пи-функция удовлетворяет рекуррентному соотношению \displaystyle{ \Pi(z) = z\Pi(z-1) }.

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

\displaystyle{ n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left(1 + \frac{1}{12 n} + \frac{1}{288 n^2} — \frac{139}{51840 n^3} — \frac{571}{2488320 n^4} + \frac{163879}{209018880 n^5} + \frac{5246819}{75246796800 n^6} + O\left(n^{-7}\right)\right), }

см. O-большое.

Во многих случаях для приближённого вычисления факториала достаточно рассматривать только главный член формулы Стирлинга:

\displaystyle{ n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n. }

При этом можно утверждать, что

\displaystyle{ \sqrt{2\pi n}\left(\frac{n}{e}\right)^n e^{1/(12n+1)}\lt n! \lt \sqrt{2\pi n}\left(\frac{n}{e}\right)^n e^{1/(12n)}. }

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

• 100! ≈ 9,33×10157;
• 1000! ≈ 4,02×102567;
• 10 000! ≈ 2,85×1035 659.

Разложение на простые множители

Каждое простое число p входит в разложение n! на простые множители в степени определяемой следующей формулой:

\displaystyle{ \left\lfloor \frac{n}{p}\right\rfloor + \left\lfloor \frac{n}{p^2}\right\rfloor + \left\lfloor \frac{n}{p^3}\right\rfloor + \ldots. }

Таким образом,

\displaystyle{ n! = \prod_{p} p^{\lfloor \frac{n}{p}\rfloor + \lfloor \frac{n}{p^2}\rfloor +\ldots}, }

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1; следовательно, произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции

Для целого неотрицательного числа n:

\displaystyle{ \left( x^n \right)^{(n)}=n! }

Например:

\displaystyle{ \left( x^5 \right)^{(5)}
= \left( 5 \cdot x^4 \right)^{(4)}
= \left( 5 \cdot 4 \cdot x^3 \right)»’
= \left( 5 \cdot 4 \cdot 3 \cdot x^2 \right)»
= \left( 5 \cdot 4 \cdot 3 \cdot 2 \cdot x \right)’
= {5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 5! }

Другие свойства

Для натурального числа \displaystyle{ n }:

\displaystyle{ n!^2 \geqslant n^n \geqslant n! \geqslant n }

Для любого \displaystyle{ n\gt 1 }:

\displaystyle{ n! } не является квадратом целого числа;

Для любого \displaystyle{ n\gt 4 }:

\displaystyle{ n! } оканчивается на 0;

Для любого \displaystyle{ n\gt 9 }:

\displaystyle{ n! } оканчивается на 00.

Если \displaystyle{ n } простое число:

\displaystyle{ (n-1)!+1 } делится на \displaystyle{ n } (теорема Вильсона)

Циклы с параметрами

Цель: дать понятие о циклах с параметром, блок-схемах, изображающих такие циклы. Учить на частных примерах составлять блок-схемы и программы с циклами; дать понятие о различиях между циклами с предусловием, постусловием и циклом с параметром; учить в одной программе использовать разные циклы, если программа содержит несколько циклов; вводить и выполнять программы, используя компиляторы BPW или Turbo Pascal.

1. Оператор цикла for … to … do …

Иногда заранее известно, сколько раз должен выполняться цикл. Для задач такого типа в языке Паскаль имеются операторы циклов с параметрами.
Формат записи таких операторов следующий: for <пар.цикла> := <нач.знач> to <кон.знач.> do <оператор>.
Здесь for, to, do — зарезервированные слова (для, до, выполнить);
<пар. цикла> — параметр цикла — переменная типа integer (точнее, любого порядкового типа);
<нач. знач.> — начальное значение — число или выражение того же типа;
<кон. знач.> — конечное значение — число или выражение того же типа;
<оператор> — произвольный оператор Паскаля.
Если операторов несколько, тогда, как и в операторе while … do …, используются операторные скобки: begin … end.
Например, возможны такие записи оператора цикла:

for i := a to b do s1;

for j := a to b do begin s1; s2; …, sn end; или

for k := p to m do    begin
s1;
s2;
…
sn     end;

Здесь s1, s2, s3, … sn — операторы цикла.
При выполнении оператора for вначале вычисляется выражение <нач .знач.> и осуществляется присваивание его значения переменной цикла
<пар .цикла> := <нач. знач.>.
После этого циклически повторяются:
1) проверка условия <пар .цикла>  <кон. знач.>; если условие не выполнено, оператор for завершает работу;
2) выполнение оператора <оператор> или операторов s1; s2; s3; … sn;
3) переменная цикла <пар. цикла> увеличивается на единицу.

Надо сразу заметить, что задать шаг цикла, отличный от 1 в этом операторе, нельзя.

Графическое изображение циклов for будет таким (см. рис. 33): Рис. 33

Здесь: i — переменная цикла; n — ее начальное значение; k — ее конечное значение. Тело цикла составляет оператор или несколько операторов: s1; s2; … sn;, которые нарисованы в прямоугольнике.

Для иллюстрации работы оператора for рассмотрим пример уже ставший традиционным при изучении работы этого оператора.

Пример 1. Составить программу вычисления факториала числа n, т. е. n!.

Вспомним из математики, что факториал числа n равен произведению чисел от 1 до n.
Например:

Замечание. В математике принято: 0! = 1.

Блок-схема

Рис. 34

Программа

Program Problem1; { Вычисление факториала числа n! }uses WinCrt; var           n, f, i : longint; begin
write(«Введите натуральное число «); readln(n);
f := 1; if n <> 0 then for i := 1 to n do f := f*i;
writeln(«Факториал числа «, n, » равен «, f) end.

Переменная n — для вводимого пользователем числа, факториал которого надо найти; f — переменная, в которой будет «накапливаться» значение факториала числа n; i — переменная цикла.
Устанавливается первоначальное значение переменной f := 1.
Далее начинается цикл. Переменной i присваивается начальное значение 1; оно сравнивается с конечным — n (1 <= n), если условие истинно, тогда выполняется оператор (в этой программе он один): f := f*i, 1*1=1; значение переменной цикла увеличивается на 1, т. е. станет равным: i := i + 1, 1 + 1 = 2 и цикл повторяется. Когда значение i станет равным n, тогда цикл выполнится последний раз, потому что следующее значение i будет n + 1, что больше конечного значения n, условие i <= n — ложно, цикл не выполняется.

Серии обратных чисел

обратными факториалами образуют сходящийся ряд, сумма которого равна экспоненциальному основанию е :

∑ N знак равно 0 ∞ 1 N! = 1 1 + 1 1 + 1 2 + 1 6 + 1 24 + 1 120 + ⋯ = е. {\ displaystyle \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {n!}} = {\ frac {1} {1}} + {\ frac {1} {1}} + {\ frac {1} {2}} + {\ frac {1} {6}} + {\ frac {1} {24}} + {\ frac {1} {120}} + \ cdots = e \,.}

Хотя сумма этого ряда является иррациональным числом, можно умножить факториалы на положительные целые числа, чтобы получить сходящийся ряд с рациональной суммой:

∑ n = 0 ∞ 1 (п + 2) п! = 1 2 + 1 3 + 1 8 + 1 30 + 1 144 + ⋯ = 1. {\ displaystyle \ sum _ {n = 0} ^ {\ infty} {\ frac {1} {(n + 2) n!}} = {\ frac {1} {2}} + {\ frac {1} {3}} + {\ frac {1} {8}} + {\ frac {1} {30}} + {\ frac {1} {144}} + \ cdots = 1 \,.}

сходимость этого ряда к 1 видна из того факта, что его частичные суммы равны k! — 1 тыс.! {\ displaystyle {\ frac {k! -1} {k!}}}. Следовательно, факториалы не образуют иррациональной последовательности.

Как использовать этот факторный калькулятор:

Вычисление факториалов становится очень простым с этим бесплатным калькулятор факториалов, который определяет точные результаты заданных чисел.

Читать дальше!

Чтобы вычислить простой факториал (найдите n!):

Чтобы найти n !, просто выполните следующие действия:

Входы:

• Прежде всего, введите номер, для которого вы хотите показать результат, в предназначенное для этого поле.

• Затем нажмите кнопку «Рассчитать».

Выходы:

После ввода в поле калькулятор показывает:

• Факториал числа.

• Пошаговые (расчеты).

Чтобы вычислить арифметические операции:

Чтобы выполнять арифметические операции с факториалом заданных чисел, просто придерживайтесь следующих пунктов:

Входы:

• Прежде всего, введите первое число.

• Совсем рядом, плагин второй номер.

• Наконец, нажмите кнопку «Рассчитать».

Выходы:

Калькулятор показывает:

• Факториал обоих чисел.

• Арифметическая операция над факториалом двух чисел в соответствии с выбранной опцией.

• Пошаговые расчеты.

Скорость роста и приближения для больших n

По мере роста n факториал n! увеличивается быстрее, чем все полиномы и экспоненциальные функции (но медленнее, чем nn {\ displaystyle n ^ {n}}и двойные экспоненциальные функции ) в п.

Максимальное приближение для n! основаны на приближении его натурального логарифма

ln ⁡ n! Знак равно ∑ x знак равно 1 n ln ⁡ x. {\ displaystyle \ ln n! = \ sum _ {x = 1} ^ {n} \ ln x \,.}

График функции f (n) = ln n! показан на рисунке справа. Это выглядит приблизительно linear для всех разумных значений n, но эта интуиция неверна. Мы получаем одно из простейших приближений для ln n! ограничивая сумму интегралом сверху и снизу следующим образом:

∫ 1 n ln ⁡ xdx ≤ ∑ x = 1 n ln ⁡ x ≤ ∫ 0 n ln ⁡ (x + 1) dx {\ displaystyle \ int _ {1} ^ {n} \ ln x \, dx \ leq \ sum _ {x = 1} ^ {n} \ ln x \ leq \ int _ {0} ^ {n} \ ln (x + 1) \, dx}

что дает нам оценку

n ln ⁡ (ne) + 1 ≤ ln ⁡ n! ≤ (п + 1) дп (п + 1 е) + 1. {\ displaystyle n \ ln \ left ({\ frac {n} {e}} \ right) +1 \ leq \ ln n! \ leq (n + 1) \ ln \ left ({\ frac {n + 1}) {e}} \ right) +1 \,.}

Следовательно, ln n! ∼ n ln n (см. ). Этот результат играет ключевую роль в анализе вычислительной сложности алгоритмов сортировки (см. сравнительная сортировка ). С границ на ln n! Выведено выше, мы получаем, что

(n e) n e ≤ n! ≤ (п + 1 е) п + 1 е. {\ displaystyle \ left ({\ frac {n} {e}} \ right) ^ {n} e \ leq n! \ leq \ left ({\ frac {n + 1} {e}} \ right) ^ { n + 1} e \,.}

Иногда бывает полезно использовать более слабые, но более простые оценки. Используя приведенную выше формулу, легко показать, что для всех n мы имеем (n / 3) 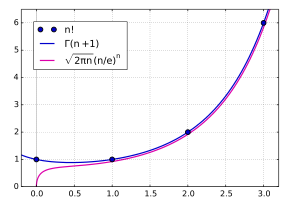Сравнение приближения Стирлинга с факториалом

Для больших n мы получаем лучшую оценку числа n! с использованием приближения Стирлинга :

n! ∼ 2 π n (n e) n. {\ displaystyle n! \ sim {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} \,.}

На самом деле это происходит из асимптотический ряд для логарифма, а факториал n лежит между этим и следующим приближением:

2 π n (ne) n

Другое приближение для ln n! дается Шриниваса Рамануджаном (Рамануджан 1988)

ln ⁡ n! ≈ n ln ⁡ n — n + ln ⁡ (n (1 + 4 n (1 + 2 n))) 6 + пер ⁡ π 2 ⟹ N! ≈ 2 π N (ne) n (1 + 1 2 n + 1 8 n 2) 1/6. {\ displaystyle {\ begin {align} \ ln n! \ приблизительно n \ ln n-n + {\ frac {\ ln {\ Bigl (} n {\ bigl (} 1 + 4n (1 + 2n) {\ bigr)} {\ Bigr)}} {6}} + {\ frac {\ ln \ pi} {2}} \\ \ Longrightarrow \; n! \ приблизительно {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ { n} \ left (1 + {\ frac {1} {2n}} + {\ frac {1} {8n ^ {2}}} \ right) ^ {1/6} \,. \ end {выровнено}} }

Как это приближение, так и приближение Стирлинга дают относительную ошибку порядка 1 / n, но приближение Рамануджана примерно в четыре раза точнее. Однако, если мы используем два поправочных члена в приближении типа Стирлинга, как в приближении Рамануджана, относительная ошибка будет порядка 1 / n:

n! ≈ 2 π n (ne) n exp ⁡ (1 12 n — 1360 n 3). {\ displaystyle n! \ приблизительно {\ sqrt {2 \ pi n}} \ left ({\ frac {n} {e}} \ right) ^ {n} \ exp \ left ({{\ frac {1} {12n}} — {\ frac {1} {360n ^ {3}}}} \ right) \,.}

Свойства[править | править код]

Факториал может быть задан следующей рекуррентной формулой:

Комбинаторная интерпретацияправить | править код

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов.

Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения  — количество перестановок пустого множества равно единице. Кроме того, формула для числа размещений из элементов по

при обращается в формулу для числа перестановок из элементов (порядка ), которое равно .

Связь с гамма-функциейправить | править код

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

.

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при .

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция , которая при может быть определена как

(интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: . Как и факториал, пи-функция удовлетворяет рекуррентному соотношению .

Формула Стирлингаправить | править код

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое.

Во многих случаях для приближённого вычисления факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

• 100! ≈ 9,33×10157;
• 1000! ≈ 4,02×102567;
• 10 000! ≈ 2,85×1035 659.

Разложение на простые множителиправить | править код

Каждое простое число p входит в разложение n! на простые множители в степени определяемой следующей формулой:

Таким образом,

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1; следовательно, произведение можно брать лишь по простым p, не превосходящим n.

Для целого неотрицательного числа n:

Например:

Другие свойстваправить | править код

Для натурального числа :

Для любого :

не является квадратом целого числа;

Для любого :

оканчивается на 0;

Для любого :

оканчивается на 00.

Если простое число:

делится на (теорема Вильсона)

Какие свойства и формулы есть у факториалов

Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:

• Факториал нуля равен единице — 0! = 1.
• Факториал единицы тоже равен единице: 1! = 1.
• Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.

Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.

Формула Стирлинга

Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:

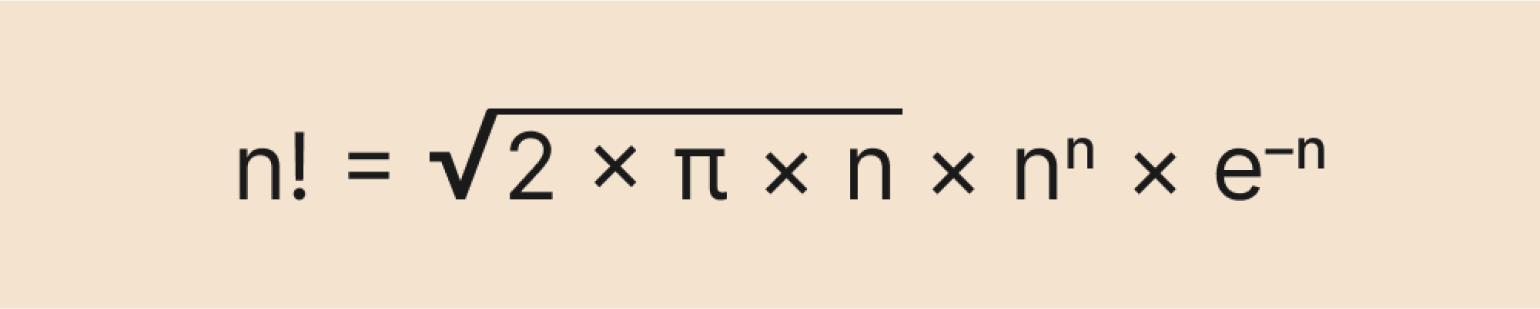
Изображение: Skillbox Media

Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).

Онлайн-калькулятор не справился с вычислением такого большого числа, как факториал 10 024Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media

Давайте попробуем вычислить факториал числа 6 по этой формуле:

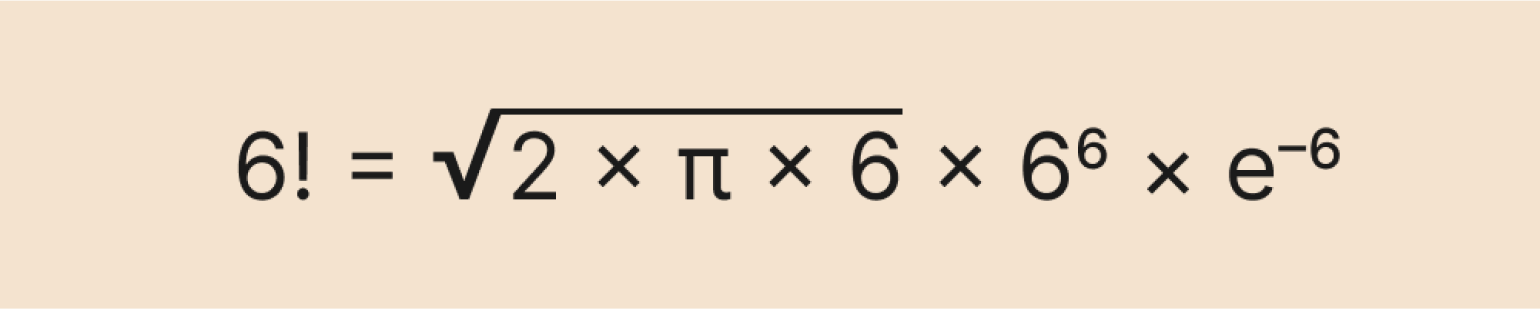
Изображение: Skillbox Media

Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:

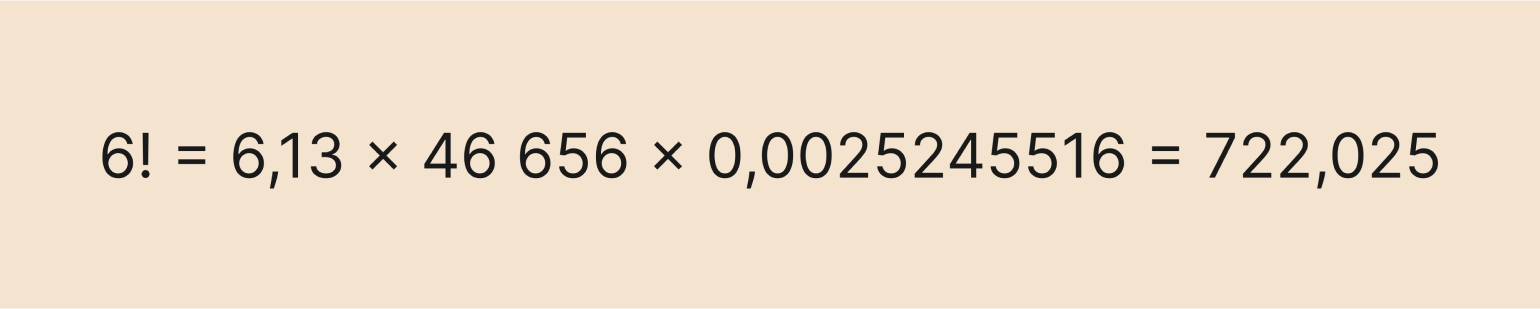
Изображение: Skillbox Media

Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:

Изображение: Skillbox Media

Это уже больше похоже на правду. Хотя погрешность всё равно есть.

Рекуррентная формула

Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:

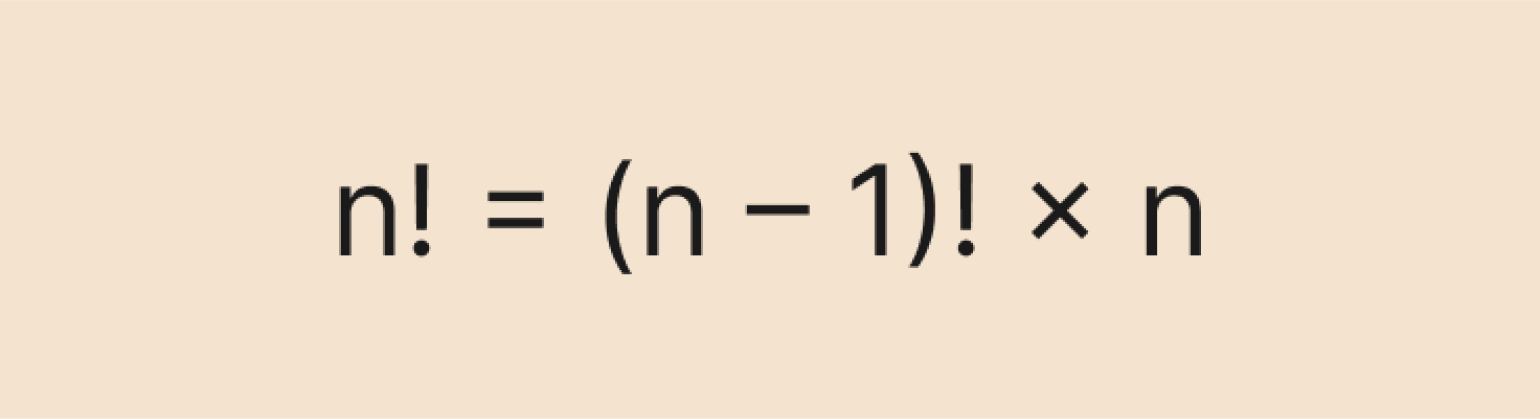
Изображение: Skillbox Media

В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.

Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.

Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:

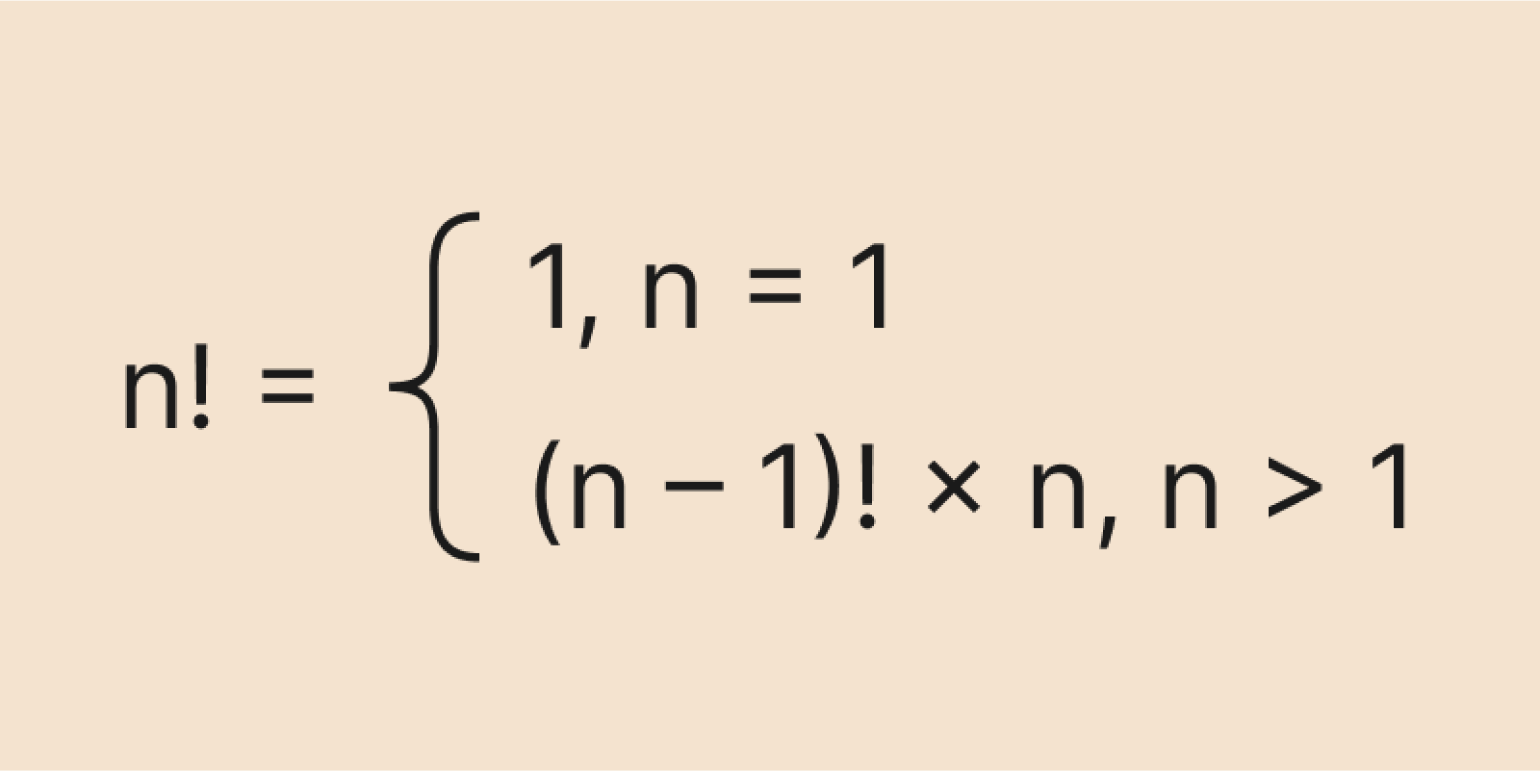
Изображение: Skillbox Media

Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.

Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:

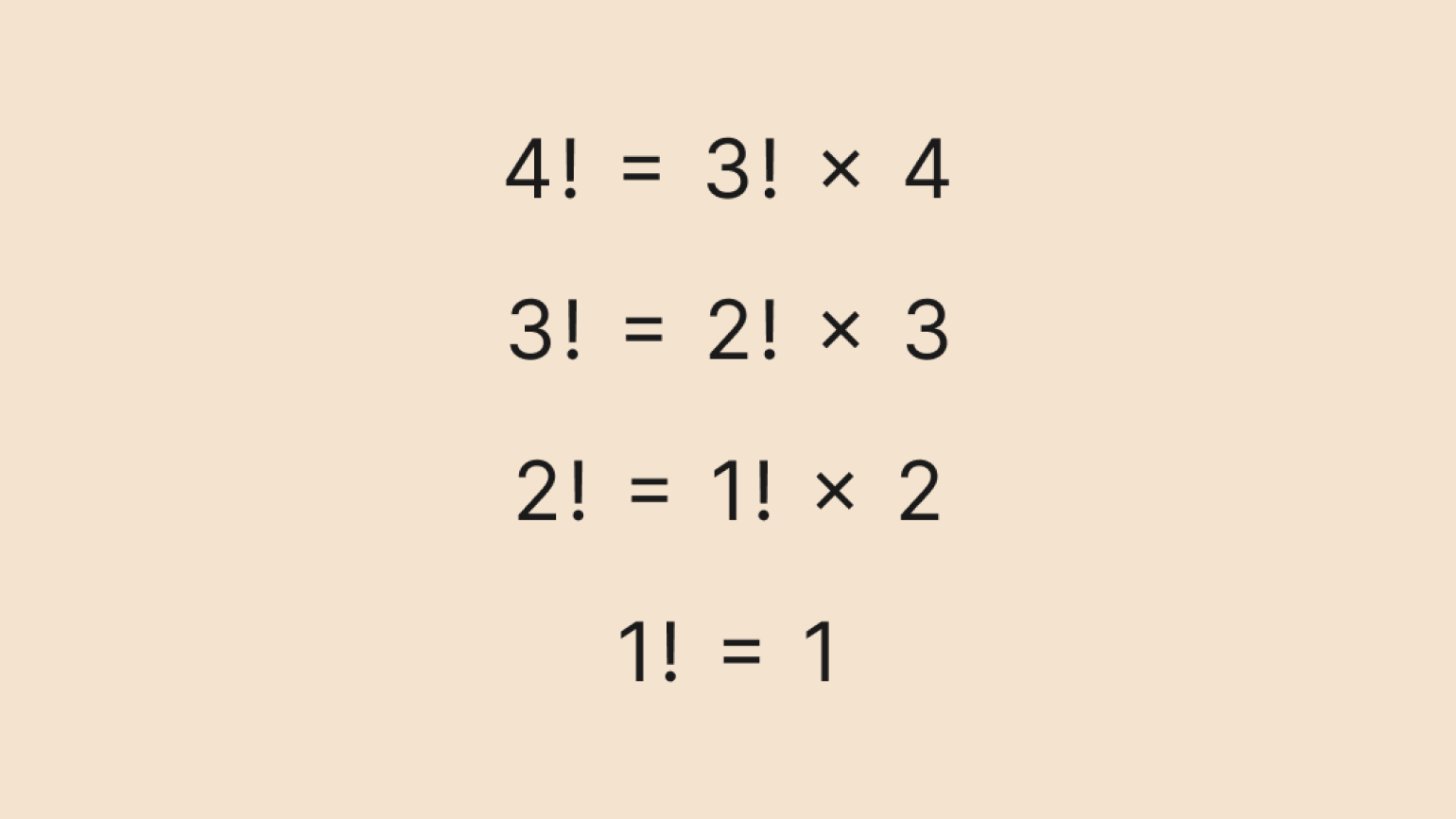
Изображение: Skillbox Media

Можно записать это и в сокращённом виде:

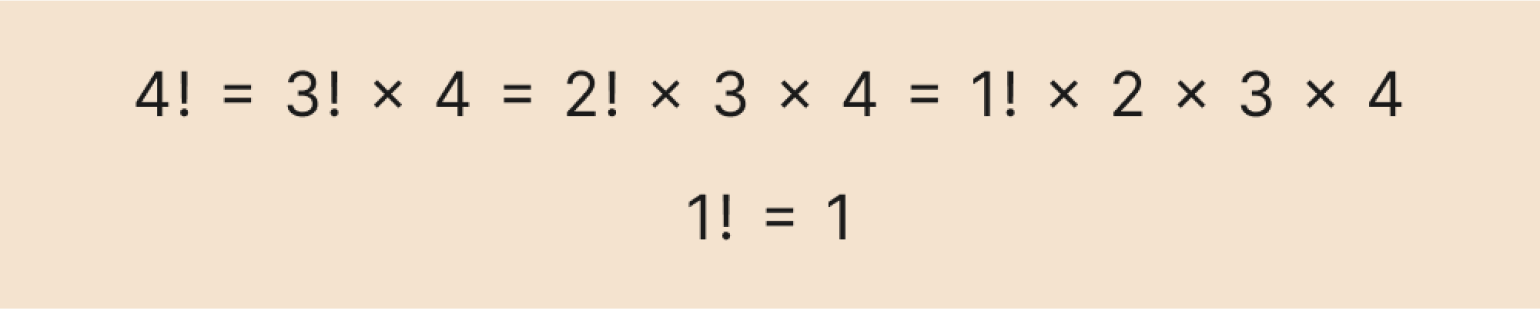
Изображение: Skillbox Media

Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:

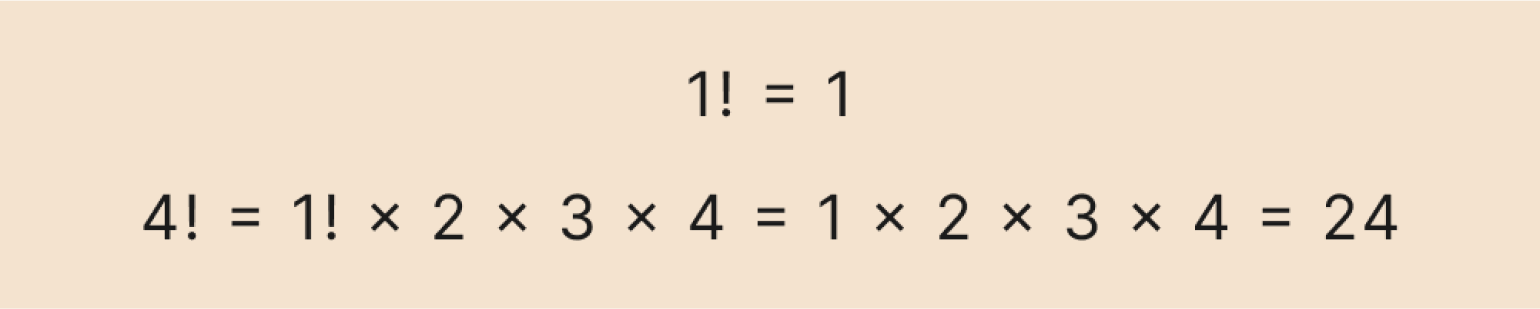
Изображение: Skillbox Media

Получили ответ — 24. Ничего сложного, просто перемножаем числа.

Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:

Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.