Найти площадь треугольника формула герона

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

• A (x1; y1);
• B (x2; y2);
• C (x3; y3).

Тогда координаты его векторов AB- и AC- выразятся так:

• AB- = (x2-x1; y2-y1);
• AC- = (x3-x1; y3-y1).

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

h = AB*sin (α).

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½* = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

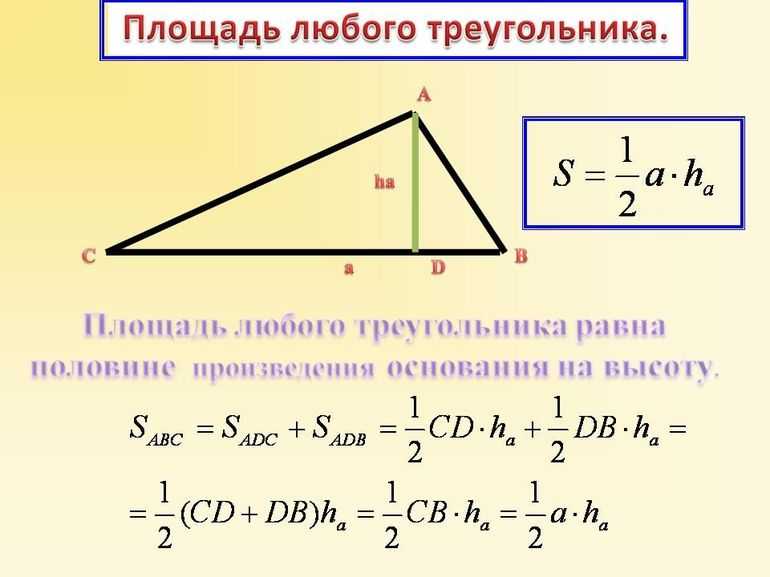
1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Калькулятор площади треугольника по трем сторонам

Удобная навигация по статье:

Как рассчитать площадь треугольника

Как известно, треугольником принято называть плоскую геометрическую фигуру, многоугольник, который ограничен минимальным количеством сторон. Также, стоит помнить, что всякий многоугольник делится на определённое количество треугольников.

Для этого необходимо соединить его вершины такими отрезками, которые не пересекали бы его стороны. Вот почему, зная как рассчитать площадь треугольника, Вы можете получить площадь большинства геометрических фигур.

Формула Герона для вычисления площади треугольника по трем сторонам

В том случае если нам известны параметры каждой стороны нашего треугольника, мы можем рассчитать площадь фигуры по формуле Герона. Для её упрощения следует применить новую величину, так называемый полупериметр, который является суммой всех сторон треугольника, которая разделена пополам.

После получения значения полупериметра, Вы можете приступать к расчёту площади по руководствуясь следующей формулой: S = sqrt(p(p-a)(p-b)(p-c)), в которой «p» – полупериметр, «a,b,c» – стороны фигуры и sqrt –квадратный корень.

Пример вычисления площади треугольника по трем сторонам

Рассмотрим на примере вычисление площади треугольника по формуле Герона.

p = (a + b + c)/ 2  где p – половина периметра треугольника.

таким образом S = √ p ( p – a ) ( p – b ) ( p – c ) .

(Это также называется формулой Герона)

Дано:

Треугольник со сторонами a = 4, b = 5, c = 3.

Задание:Найдите площадь треугольника

Решение:

Используйте формулу половинного периметра:

p = (3 + 4 + 5)/ 2= 6

Полученные значения подставляем в формулу Герони:

S = √ 6 ( 6 – 3 ) ( 6 – 4 ) ( 6 – 5 ) =

√ 6 ⋅ 3 ⋅ 2 ⋅ 1 = √ 36 =6

Ответ: 6

Историческая справка

Формула приписывается Герону, живущему в  Александрии, который был греческим инженером и математиком в 10 – 70 годах нашей эры

Среди прочего, он разработал  первый известный паровой двигатель, но его рассматривали как игрушку!

Площадь трапеции

Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.

В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:

Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:

Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:

В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:

Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.

Решение. Это простая задача на использование формулы площади трапеции:

Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):

Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:

Считаем площадь:

Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?

Решение. Выполним построение:

Найдем острый угол трапеции. Так как CD||АВ, то

Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:

ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:

Из равенства треуг-ков следует, что

Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.

Понятие площади

Определение

Площадью (S) геометрической фигуры именуется численная величина, характеризующая её размер.

В этом собственно и состоит понятие площади. У неё есть следующие два свойства:

1. Площадь равных геометрических фигур имеет одно и то же числовое значение;
2. Величина площади фигуры равняется сумме единичных площадей квадратов, на которые её можно разделить.

Пример 1.

Пусть у нас имеется прямоугольник в котором укладывается 7 клеток по вертикали и 12 по горизонтали. Это значит он будет иметь стороны a=7 и b=12.

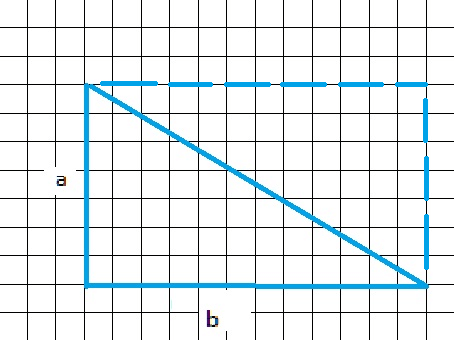
Из рисунка видно, что S нашего треугольника это половина таковой у прямоугольника.  Последняя вычисляется так \. Чтобы узнать площадь треугольника, разделим \ на 2, тогда получим:

Формула 1

Подставляем численные значения (7*12)/2 = 42.

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: . Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Формулы площади треугольника

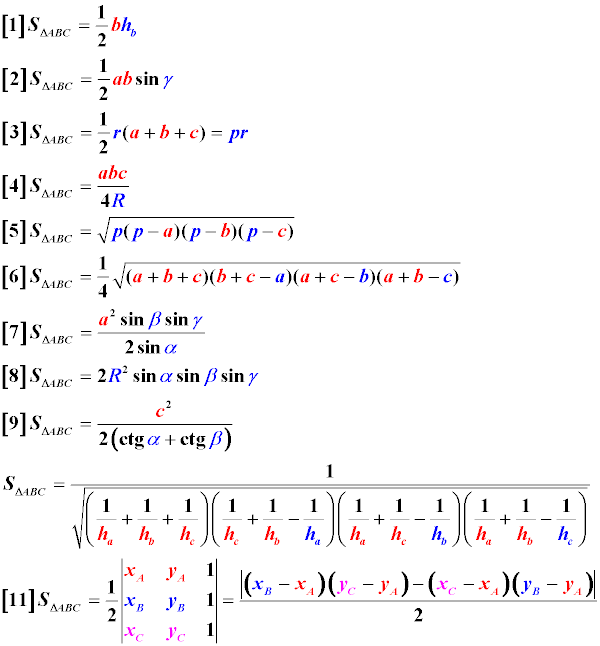
Пояснения к формулам: a, b, c — длины сторон треугольника, площадь которого мы хотим найти r — радиус вписанной в треугольник окружности R — радиус описанной вокруг треугольника окружности h — высота треугольника, опущенная на сторону p — полупериметр треугольника, 1/2 суммы его сторон (периметра) α — угол, противолежащий стороне a треугольника β — угол, противолежащий стороне b треугольника γ — угол, противолежащий стороне c треугольника h_a, h_b, h_c — высота треугольника, опущенная на сторону a, b, c

Обратите внимание, что приведенные обозначения соответствуют рисунку, который находится выше, чтобы при решении реальной задачи по геометрии Вам визуально было легче подставить в нужные места формулы правильные значения.

Площадь треугольника равна половине произведения высоты треугольника на длину стороны на которую эта высота опущена (Формула 1). Правильность этой формулы можно понять логически. Высота, опущенная на основание, разобьет произвольный треугольник на  два прямоугольных. Если достроить каждый из них до прямоугольника с размерами b и h, то, очевидно, площадь данных треугольников будет равна ровно половине площади прямоугольника (Sпр = bh)
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними (Формула 2 ) (см. пример решения задачи с использованием этой формулы ниже). Несмотря на то, что она кажется непохожей на предыдущую, она легко может быть в нее преобразована. Если из угла B опустить высоту на сторону b, окажется, что произведение стороны a на синус угла γ по свойствам синуса в прямоугольном треугольнике равно проведенной нами высоте треугольника, что и даст нам предыдущую формулу
Площадь произвольного треугольника может быть найдена через произведение половины радиуса вписанной в него окружности на сумму длин всех его сторон (Формула 3), проще говоря, нужно полупериметр треугольника умножить на радиус вписанной окружности (так легче запомнить)
Площадь произвольного треугольника можно найти, разделив произведение всех его сторон на 4 радиуса описанной вокруг него окружности (Формула 4)
Формула 5 представляет собой нахождение площади треугольника через длины его сторон и его полупериметр (половину суммы всех его сторон)

Формула Герона (6) — это представление той же самой формулы без использования понятия полупериметра, только через длины сторон
Площадь произвольного треугольника равна произведению квадрата стороны треугольника на синусы прилежащих к этой стороне углов деленного на двойной синус противолежащего этой стороне угла (Формула 7)
Площадь произвольного треугольника можно найти как произведение двух квадратов описанной вокруг него окружности на синусы каждого из его углов. (Формула
Если известна длина одной стороны и величины двух прилежащих к ней углов, то площадь треугольника может быть найдена как квадрат этой стороны, деленный на двойную сумму котангенсов этих углов (Формула 9)
Если известна только длина каждой из высот треугольника (Формула 10), то площадь такого треугольника обратно пропорциональна длинам этих высот, как по Формуле Герона
Формула 11 позволяет вычислить площадь треугольника по координатам его вершин, которые заданы в виде значений (x;y) для каждой из вершин

Обратите внимание, что получившееся значение необходимо взять по модулю, так как координаты отдельных (или даже всех) вершин могут находиться в области отрицательных значений

См. также площадь равнобедренного треугольника.

Примечание. Далее приведены примеры решения задач по геометрии на нахождение площади треугольника. Если Вам необходимо решить задачу по геометрии, похожей на которую здесь нет — пишите об этом в форуме. В решениях вместо символа «квадратный корень» может применяться функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Иногда для простых подкоренных выражений может использоваться символ √

История

Формула зачисляются Heron (или герой) Александрийский , и доказательство можно найти в его книге Метрики , написанной около 60 г. н.э. Было высказано предположение , что Архимед знал формулу более двух веков назад, и с тех пор Metrica представляет собой сборник математические знания, доступные в древнем мире, вполне возможно, что формула предшествует ссылке, приведенной в этой работе.

Формула, эквивалентная формуле Герона, а именно:

А знак равно 1 2 а 2 c 2 — ( а 2 + c 2 — б 2 2 ) 2 > c ^ — \ left ( + c ^ -b ^ > > \ right) ^ >>>

был открыт китайцами независимо от греков. Он был опубликован в « Математическом трактате в девяти разделах» ( Цинь Цзюшао , 1247).

Формулы, которыми можно воспользоваться в разных задачах

Известны длины сторон, и требуется найти площадь равнобедренного треугольника.

В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:

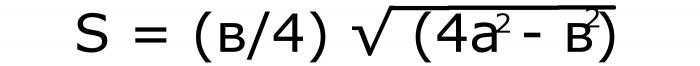
Пусть она будет записана под №1.

Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.

Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:

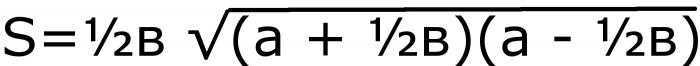
Это формула №2.

Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.

Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:

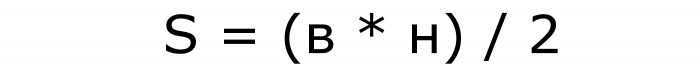
Номер этой формулы — 3.

В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.

Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:

Порядковый номер формулы — 4.

В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.

Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:

Ее номер — 5.

Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.

Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:

Номер последней формулы — 6.

Как найти площадь треугольника по трем сторонам

Представлено множество вариантов для расчёта длины сторон радиуса и площади треугольника. Одна из удобных формул для расчёта площади по трём сторонам называется формулой Герона и используется в том случае, если известна длина всех трех сторон.

Полупериметром называют сумму длин всех сторон разделенную на 2.

Рассмотрим формулу на примере. Нам необходимо найти полупериметр треугольника, где даны следующие стороны  a = 5, b = 6, c = 7. Производим расчет:

Вычисляя по формуле Герона, вначале мы перемножили полученные результаты, затем из полученного числа извлекли квадратный корень. Конечное значение и является площадью искомого треугольника.

Для полного понимания необходимо постоянно упражняться и заниматься. С каждым разом усложняйте задачу и выбирайте примеры  с другими значениями.  Систематическое повторение позволит назубок выучить формулу Герона и научиться применять её для решения простых и сложных задач.

Геометрия может пригодиться не только в школе, но и во взрослой жизни, например, тем, кто занимается обустройством интерьера, ремонтами и планирует изучать архитектуру.

Доказательства

В первоначальном доказательстве Герона использовались циклические четырехугольники . Другие аргументы апеллируют к тригонометрии, как показано ниже, или к центру и одной вневписанной окружности треугольника, или к теореме Де Гуа (для частного случая острых треугольников).

Тригонометрическое доказательство с использованием закона косинусов

Далее следует современное доказательство, основанное на алгебре и весьма отличное от доказательства Герона (в его книге «Метрика»). Пусть a , b , c — стороны треугольника, а α , β , γ — углы, противоположные этим сторонам. Применяя закон косинусов, получаем

потому что ⁡ γ знак равно а 2 + б 2 — c 2 2 а б + b ^ -c ^ > >>

Из этого доказательства мы получаем алгебраическое утверждение, что

грех ⁡ γ знак равно 1 — потому что 2 ⁡ γ знак равно 4 а 2 б 2 — ( а 2 + б 2 — c 2 ) 2 2 а б . \ gamma>> = b ^ — (a ^ + b ^ -c ^ ) ^ >> >.>

Высота треугольника на базовой а имеет длину б зш Г , и следует

А знак равно 1 2 ( база ) ( высота ) знак равно 1 2 а б грех ⁡ γ знак равно 1 4 4 а 2 б 2 — ( а 2 + б 2 — c 2 ) 2 знак равно 1 4 ( 2 а б — ( а 2 + б 2 — c 2 ) ) ( 2 а б + ( а 2 + б 2 — c 2 ) ) знак равно 1 4 ( c 2 — ( а — б ) 2 ) ( ( а + б ) 2 — c 2 ) знак равно ( c — ( а — б ) ) ( c + ( а — б ) ) ( ( а + б ) — c ) ( ( а + б ) + c ) 16 знак равно ( б + c — а ) 2 ( а + c — б ) 2 ( а + б — c ) 2 ( а + б + c ) 2 знак равно ( а + б + c ) 2 ( б + c — а ) 2 ( а + c — б ) 2 ( а + б — c ) 2 знак равно s ( s — а ) ( s — б ) ( s — c ) . A & = > (>) (>) \\ & = > ab \ sin \ gamma \\ & = > b ^ — (a ^ + b ^ — c ^ ) ^ >> \\ & = > + b ^ -c ^ )) (2ab + (a ^ + b ^ -c ^ ))>> \\ & = > — (ab) ^ ) ((a + b) ^ -c ^ )>> \\ & = >> \\ & = > > > >>> \\ & = > > > >>> \\ & = >. \ end >>

Разность двух квадратов факторизации был использован в двух различных этапов.

Алгебраическое доказательство с использованием теоремы Пифагора

Следующее доказательство очень похоже на доказательство Raifaizen. По теореме Пифагора мы имеем b 2 = h 2 + d 2 и a 2 = h 2 + ( c — d ) 2 согласно рисунку справа. Вычитание этих значений дает a 2 — b 2 = c 2 — 2 кд . Это уравнение позволяет нам выразить d через стороны треугольника:

d знак равно — а 2 + б 2 + c 2 2 c . + b ^ + c ^ > >.>

Для высоты треугольника h 2 = b 2 — d 2 . Заменяя d на формулу, приведенную выше, и применяя тождество разности квадратов, мы получаем

час 2 знак равно б 2 — ( — а 2 + б 2 + c 2 2 c ) 2 знак равно ( 2 б c — а 2 + б 2 + c 2 ) ( 2 б c + а 2 — б 2 — c 2 ) 4 c 2 знак равно ( ( б + c ) 2 — а 2 ) ( а 2 — ( б — c ) 2 ) 4 c 2 знак равно ( б + c — а ) ( б + c + а ) ( а + б — c ) ( а — б + c ) 4 c 2 знак равно 2 ( s — а ) ⋅ 2 s ⋅ 2 ( s — c ) ⋅ 2 ( s — б ) 4 c 2 знак равно 4 s ( s — а ) ( s — б ) ( s — c ) c 2 . h ^ & = b ^ — \ left ( + b ^ + c ^ > > \ right) ^ \\ & = + b ^ + c ^ ) (2bc + a ^ -b ^ -c ^ )> >> \\ & = (b + c) ^ -a ^ a ^ — (bc) ^ > >> \\ & = >> \\ & = >> \\ & = >>. \ End >>

Теперь применим этот результат к формуле, которая вычисляет площадь треугольника по его высоте:

А знак равно c час 2 знак равно c 2 4 ⋅ 4 s ( s — а ) ( s — б ) ( s — c ) c 2 знак равно s ( s — а ) ( s — б ) ( s — c ) . A & = > \\ & = > > \ cdot >>>> \\ & = >. \ end >>

Тригонометрическое доказательство с использованием закона котангенсов

Из первой части доказательства закона котангенсов получаем, что площадь треугольника равна

А знак равно р ( ( s — а ) + ( s — б ) + ( s — c ) ) знак равно р 2 ( s — а р + s — б р + s — c р ) знак равно р 2 ( детская кроватка ⁡ α 2 + детская кроватка ⁡ β 2 + детская кроватка ⁡ γ 2 ) A & = r (sa) + (sb) + (sc) = r ^ \ left ( > + > + > \ right) \\ & = r ^ \ left (\ cot > + \ cot > + \ cot > \ right) \ end >>

и A = rs , но, поскольку сумма полууглов равна π / 2, применяется тождество тройного котангенса , поэтому первый из них равен

А знак равно р 2 ( детская кроватка ⁡ α 2 детская кроватка ⁡ β 2 детская кроватка ⁡ γ 2 ) знак равно р 2 ( s — а р ⋅ s — б р ⋅ s — c р ) знак равно ( s — а ) ( s — б ) ( s — c ) р . A & = r ^ \ left (\ cot > \ cot > \ cot > \ right) = r ^ \ left ( > \ cdot > \ cdot > \ right) \\ & = >. \ end >>

Комбинируя два, получаем

А 2 знак равно s ( s — а ) ( s — б ) ( s — c ) , = s (sa) (sb) (sc),>

из чего следует результат.

Формула Герона

Введем и докажем теорему о нахождении площади треугольника по трем известным сторонам. Эта формула носит название формулы Герона.

Пусть нам даны три стороны треугольника $a, b и c$. Тогда площадь этого треугольника выражается следующим образом

где $p$ — полупериметр данного треугольника.

Доказательство.

Будем пользоваться обозначениями, введенными на рисунке 1.

Рассмотрим треугольник $ABH$. По теореме Пифагора, получим

Очевидно, что $HC=AC-AH=b-x$

Рассмотрим треугольник $ CBH$. По теореме Пифагора, получим

Приравняем значения квадрата высоты из двух полученных соотношений

Из первого равенства найдем высоту

Так как полупериметр равен $p=frac<2>$, то есть $a+b+c=2p$, то

По теореме 1, получим

Теорема доказана.

Свойства треугольника

1. длина любой стороны треугольника меньше суммы длин двух остальных сторон, но больше разницы длин двух остальных сторон;
2. высота треугольника образует прямой угол со стороной, к которой проведена;
3. площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота S_ABC=a⋅h/2.

Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 4 = 7, значит построить треугольник не получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. Так как для укаанных длин будут справедливы следующие равенства: 16 + 18 > 32 и 16 > 32 − 18, то треугольник построить получится.

Пример. Можно ли построить треугольник из отрезков с длинами: 1 см, 3 см, 7 см ?

Необходимо вспомнить следующее правило: если сумма любых двух сторон меньше либо равна оставшейся стороне, то треугольник построить не получится. 3 + 1

Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.

Пусть AB = 4 см, тогда сторона BC = 4 : 2 = 2. И тогда площадь треугольника будет равна: S = 2 * 4 : 2 = 4 см2

Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше. Определи площадь треугольника.

Пусть AB = 12 см, тогда сторона BC = 12 : 3 = 4. И тогда площадь треугольника будет равна: S = 12 * 4 : 2 = 24 см2

Рассчитай площадь треугольника ABC, если дана площадь клетки — 1 м2.

В треугольнике от вершины B проведём перпендикуляр к стороне AC. Таким образом данный треугольник разбит на два прямоугольных треугольника. Каждый из них — половина прямоугольника.

Поэтому площадь можно рассчитать следующим образом:

S_ABC=4⋅4/2+3⋅4/2=(16+12)/2=28/2=14м2.

Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.

Известно, что периметр равностороннего треугольника — 21 см.

Значит, одна сторона треугольника равна 7 см.

Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.

Дан равносторонний треугольник. 2 раза сделано следующее:

1. на всех сторонах отмечены и соединены серединные точки. 2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки. Треугольник, который образовался на этот раз, закрашен розовым цветом.

Внутренний треугольник состоит из 4 маленьких треугольников, такими же являются остальные 3 треугольника, следовательно, всего 4⋅4=16 маленьких треугольников.

2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?

Площадь большого треугольника равна 16⋅4=64 м².

3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.

4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?

Очевидно, что в каждой следующей конструкции число маленьких треугольников увеличивается в 4 раза.

Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.

Определи площадь данных фигур, если площадь одной клетки равна 6 см2. 1)

Фигура образует 2 клетки, а ее площадь равна 6 *2 = 12 кв.см.

У второй фигуры будет 8 клеток. Площадь фигуры равна 8 ⋅ 6 = 48см2 .

Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.

У третьей фигуры — 18 клеток, у четвертой — 32 клетки.

Примеры решения задач

Задача 1

Рассчитать площадь треугольника, если a=6, b=8, c=6.

Решение

\(p=\frac{6+8+6}2=10\)

Тогда площадь треугольника равна:

\(S=10\sqrt{\left(10-6\right)\left(10-8\right)\left(10-6\right)}=320\)

Ответ: 320 см2.

Задача 2

Вычислить площадь параллелограмма, если одна из его сторон равна 51, а диагонали равны 40 и 74.

Решение

Диагонали AC и BD  пересекаются в точке O.

Если  AD = 51,  AC = 40  и  BD = 74,  то  AO = 20,  OD = 37.

По формуле Герона

\(S_{ABCD} = 4S_{AOD} = \sqrt{54\left(54-51\right)\left(54-37\right)\left(54-20\right)}=1224\)

Ответ: 1224 см2. 

Задача 3

В треугольнике ABC три стороны:  AB = 26,  BC = 30  и  AC = 28. Найти часть площади этого треугольника, заключённую между высотой и биссектрисой, проведёнными из вершины B.

Решение

BP и BQ – высота и биссектриса треугольника.

По формуле Герона:

\(S=\sqrt{42\left(42-30\right)\left(42-28\right)\left(42-26\right)}=336\)

\(S = ½ AC·BP\)

Поэтому  \(BP =\frac{2S}{AC}=\frac{2\times336}{28}=24\).

По свойству биссектрисы треугольника:

\(\frac{AQ}{QC}=\frac{AB}{BC}=\frac{26}{30}=\frac{13}{15}\)

Соответственно \(AQ=\frac{13}{28}AC = 13\).

По теореме Пифагора из треугольника APB получаем:

\(AP=\sqrt{AP^2-BP^2}=\sqrt{26^2-24^2}=\sqrt{2\times50}=10\)

Следовательно,  \(PQ = AQ – AP = 13 – 10 = 3\)

\(S_{BPQ} = ½ PQ·BP = \frac{3\times24}2=36\)

Формулы для площади треугольника

      Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник			a – любая сторона,ha – , опущенная на эту сторону
		a и b – две любые стороны,С – угол между ними
		a, b, c – стороны,p –  Формулу называют «Формула Герона»
		a – любая сторона,B, С – прилежащие к ней углы
		a, b, c – стороны,r – радиус ,p –
		a, b, c  – стороны,R – радиус
	S = 2R2 sin A sin B sin C	A, B, С – углы,R – радиус
Равносторонний (правильный) треугольник			a – сторона
		h –
		r – радиус
		R – радиус
			a и b –
		a – ,φ – прилежащий острый угол
		a – ,φ – противолежащий острый угол
		c – ,φ – любой из острых углов

Произвольный треугольник
	гдеa – любая сторона,ha – , опущенная на эту сторону
	гдеa и b – две любые стороны,С – угол между ними
	гдеa, b, c – стороны,p –  Формулу называют «Формула Герона»
	гдеa – любая сторона,B, С – прилежащие к ней углы
	гдеa, b, c – стороны,r – радиус ,p –
	гдеa, b, c  – стороны,R – радиус
	S = 2R2 sin A sin B sin C гдеA, B, С – углы,R – радиус
Равносторонний (правильный) треугольник
	гдеa – сторона
	гдеh –
	гдеr – радиус
	гдеR – радиус
	гдеa и b –
	гдеa – ,φ – прилежащий острый угол
	гдеa – ,φ – противолежащий острый угол
	гдеc – ,φ – любой из острых углов

Произвольный треугольник

гдеa – любая сторона,ha – , опущенная на эту сторону

гдеa и b – две любые стороны,С – угол между ними

гдеa, b, c – стороны,p –  Формулу называют «Формула Герона»

гдеa – любая сторона,B, С – прилежащие к ней углы

гдеa, b, c – стороны,r – радиус ,p –

гдеa, b, c  – стороны,R – радиус

S = 2R2 sin A sin B sin C гдеA, B, С – углы,R – радиус

Равносторонний (правильный) треугольник

гдеa – сторона

гдеh –

гдеr – радиус

гдеR – радиус

гдеa и b –

гдеa – ,φ – прилежащий острый угол

гдеa – ,φ – противолежащий острый угол

гдеc – ,φ – любой из острых углов

Что такое треугольник

Треугольник – это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.

Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).

Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.

Вывод формул для площади равностороннего треугольника

      Утверждение 7.

1. Если a – сторона равностороннего треугольника, то его площадь

Если h – равностороннего треугольника, то его площадь

Если r – радиус , то его площадь

Если R – радиус около равностороннего треугольника окружности, то его площадь

      Доказательство.

1. Рассмотрим рисунок 7.

Рис. 7

В силу утверждения 2

Рассмотрим рисунок 8.

Рис. 8

Поскольку

то

Рассмотрим рисунок 9.

Рис. 9

Поскольку у равностороннего треугольника , то .  Следовательно,

Рассмотрим рисунок 10.

Рис. 10

Поскольку у равностороннего треугольника центр описанной окружности совпадает с точкой пересечения медиан, высот и биссектрис, то выполнено равенство Следовательно,

      Доказательство утверждения 7 завершено.