Все формулы площади трапеции и калькулятор онлайн

Площадь трапеции онлайн калькулятор (5 способов)

Этот онлайн калькулятор площади трапеции поможет найти площадь трапеции.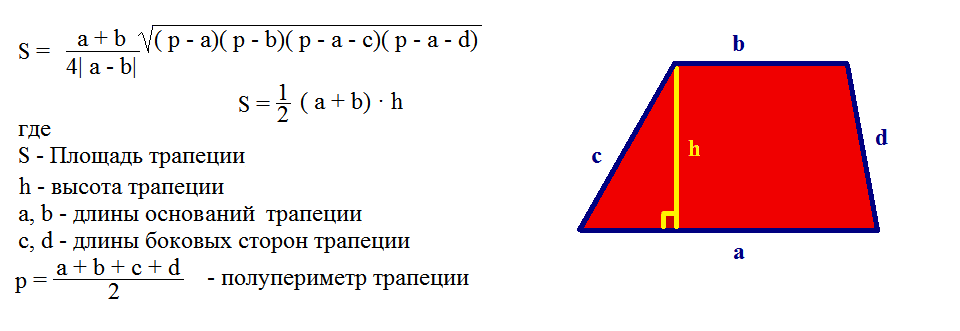

алгоритм нахождения площади трапеции.

Trapezoid area calculation method

Through bases and heightThrough the middle line and heightAlong the diagonals and the angle between themBy the lengths of all sides and basesThrough the radius of the inscribed circle and the angle

Base a:
Base b:
Side c:
Side d:

A trapezoid is a quadrilateral whose two sides are parallel (bases) and the other two are not parallel (sides).
Trapezoid area formula
where a and b are the bases, c and d are the sides

Solution:

S =

·√c2 — (

(b-a)2+c2-d2

2·(b-a)

11+16

·√242 — (

(16-11)2+242-272

2·(16-11)

·√242 — (

52+242-272

2·5

·√576 — (

25+576-729

= 13.

·√576 — (

-128

= 13.5

·√576 — (-12.8)2

= 13.5

·√576 — 163.84

= 13.5

·√412.16

= 13.5

20.302

274.077

Answer: trapezoid area with sides 11,16,24,27 equal to 274.077

Трапеция — это четырехугольник, у которого две стороны параллельны (основание), а две другие не параллельны (боковые стороны).

Площадь трапеции– это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой две противоположные стороны попарно параллельны (основания трапеции), а две другие не параллельны (стороны страпеции).

Скачать все формулы нахождения площади трапеции в формате Word

Similar calculators

Площадь прямоугольника онлайн калькулятор (6 способов)
Площадь параллелограмма онлайн калькулятор (4 способа)
Площадь квадрата онлайн калькулятор (3 способа)
Площадь ромба онлайн калькулятор (7 способов)
Площадь круга онлайн калькулятор (3 способа)

Calculators of other categories

Translating numbers from one number system to any other online
Addition, multiplication and division of numbers in different number systems
Division in a column online.

Visual division calculator.
Multiplication in a column online. Visual multiplication calculator.
The addition of the column. Visual addition calculator.

Your score?

Площадь прямоугольного треугольника — формулы и калькуляторы

Прямоугольный треугольник — это треугольник, в котором один угол прямой (90°).

По основанию и высоте площадь прямоугольно треугольника равна половине произведения катетов треугольника.

Площадь прямоугольного треугольника по двум катетам — расчет:

Формула	Результат
S = ½ × a × b
	Катет a
Катет b

Площадь прямоугольного треугольника через гипотенузу и угол:

Формула	Результат
S = ¼ × c² × sin (2α)
	Сторона c
Угол α

Площадь прямоугольного треугольника через катет и угол — онлайн калькулятор:

Формула	Результат
S = ½ × b² × tg (α)
	Сторона b
Угол α

Если в треугольник вписана окружность и известны отрезки, на которые она делит гипотенузу, то площадь прямоугольно треугольника равна произведению этих отрезков.

Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность:

Формула	Результат
S = d × e
	Отрезок d
Отрезок e

Площадь прямоугольного треугольника через гипотенузу и вписанную окружность — расчет:

Формула	Результат
S = r × (r + c)
	Сторона с
Радиус r

Площадь прямоугольно треугольника по трем сторонам (формула Герона) равна произведению разностей полупериметра треугольника и каждого из катетов. Полупериметр p = ½ × (a + b + c)

Площадь прямоугольного треугольника по формуле Герона:

Формула	Результат
S = ( ½ × (a + b + c) — a) × ( ½ × (a + b + c) — b)
	Сторона a
Сторона b
Сторона c

Формулы площади выпуклого четырехугольника

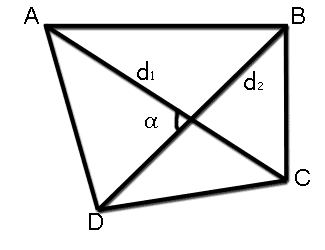
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

S = 1 ₁ ₂ sin

2

где S — площадь четырехугольника,₁, ₂ — длины диагоналей четырехугольника, — угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружностиS = ·
Формула площади четырехугольника по длине сторон и значению противоположных угловS = √()()()() — cos2

где S — площадь четырехугольника,, , , — длины сторон четырехугольника,

= + + + — полупериметр четырехугольника,

2

= + — полусумма двух противоположных углов четырехугольника.

2
Формула площади четырехугольника, вокруг которого можно описать окружностьS = √()()()()

Формула площади для квадрата и прямоугольника

Геометрия, как часть математики, рассматривает целый ряд геометрических фигур: круг, квадрат, прямоугольник, треугольник и многих других.

Геометрические фигуры являются множеством точек на плоской поверхности, которые соединяются прямыми и на выходе становятся разными фигурами с разными особенностями.

Параметры геометрических фигур, такие как длины сторон, периметр, площадь, можно находить разными способами в зависимости от типа фигуры.

Площадь в геометрии обозначается знаком S, от английского square — площадь. Понятием площади пользуются как люди науки — математики, физики, так и люди рабочих профессий, например, строители.

Данная характеристика измеряется в единицах измерения в квадрате, например, квадратный сантиметр (см2), квадратный метр (м2), гектар (га).

Квадрат и прямоугольник являются фигурами, у которых есть по 4 прямых угла. Их отличает только длина сторон — у прямоугольника не все 4 стороны равны, они равны попарно относительно противоположных.

Площадь правильно построенного прямоугольника можно найти через перемножение его сторон друг на друга.

С помощью данной формулы можно найти площади классов или комнат, а также стен, что может помочь как в решении математических, так и бытовых задач.

3d моделью прямоугольника можно считать параллелепипед.

Площадь квадрата можно найти двумя способами:

по длине стороны в квадрате;
по длине диагонали.

Так как квадрат является частным случаем прямоугольника, его площадь также можно найти по формуле S = a * b , однако в таком случае a и b будут равны, а формула по смыслу будет повторять выше написанную.

В некоторых случаях необходимо нахождение площади квадрата через диагональ. Это может быть связано с решением определенной геометрической задачи или в связи с практическим удобством.

Примеры решения задач

Найти площадь трапеции, размер одной диагонали которой равен 6 см, второй — 9 см, а угол между ними — \(30^\circ.\)

Получим: \(S = \frac\times 6 \times 9 \times \sin30^\circ = 13,5. \)

Параллельные стороны плоской геометрической фигуры равны 9 и 5 см. Расстояние между ними — 7 см. Найти площадь фигуры.

Найти площадь трапеции, если известны длины непараллельных сторон — 13 и 15 см, а также разность длин оснований — 14 см. В трапецию вписана окружность.

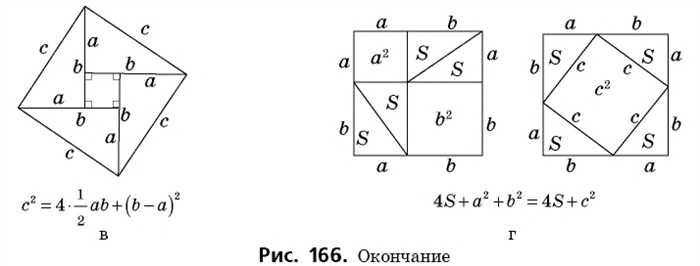
Одно из основных свойств трапеции — в нее можно вписать окружность, если сумма оснований равна сумме боковых сторон. Следовательно, если представить две проведенные высоты, как на рисунке, АК + МD = АD — BC = 14.

Поскольку углы К и М являются прямыми, воспользуемся теоремой Пифагора: \(AB^ = AK^ + BK^.\) \(BK^ = AB^ — AK^.\) \(CD^ = CM^ + MD^.\) \(CM^ = CD^ — MD^.\) \(BK = CM.\) \(AB^ — AK^ = CD^ — MD^.\)

Подставим числовые значения: \(13^ — (14 — MD)^ = 15^ — MD^.\) MD = 9 см. \(CM^ = CD^ — MD^.\)

Сложные примеры расчетов площади трапеции

Для решения более сложных задач по вычислению площади трапеции требуется провести цепочку логических вычислений, используя различные формулы и принимая во внимание условия задачи. Например, задача может состоять в вычислении площади трапеции, один из углов которой равен 60 градусам, сумма длин оснований равна 12 см, а высота равна 4 см

Например, задача может состоять в вычислении площади трапеции, один из углов которой равен 60 градусам, сумма длин оснований равна 12 см, а высота равна 4 см.

Для решения этой задачи можно воспользоваться формулой для вычисления площади трапеции по высоте:

где a и b — длины оснований, h — высота. Следует выразить одно из оснований через другое, зная их сумму и угол между ними:

Теперь, подставив выражение для a в уравнение для b, можно определить площадь трапеции:

Далее можно найти максимальное значение площади, взяв производную функции и приравняв ее к нулю:

Из этого следует, что:

Ответ: площадь трапеции равна 24 квадратные сантиметры.

Формулы площади треугольника

Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

S = 1

2
Формула площади треугольника по трем сторонам

S = √()()()
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1

2
Формула площади треугольника по трем сторонам и радиусу описанной окружности

S =

4R
Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = ·

где S — площадь треугольника, — длины сторон треугольника, — высота треугольника, — угол между сторонами и , — радиус вписанной окружности,
R — радиус описанной окружности,

= + + — полупериметр треугольника.

2

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.

Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.

Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r2/sinα. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30: S = 8r2.

Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d₁ и d₂, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h2.

Свойства

Трапеция является фигурой с двумя параллельными противоположными сторонами, при этом все четыре стороны могут быть разной длины. Параллельные стороны b и d называются меньшим и большим основанием трапеции, a и c – боковыми сторонами. Зная стороны трапеции, можно найти все характеризующие ее параметры. Периметр трапеции, зная стороны, представляет собой их сумму. P=a+b+c+d

Высота трапеции является перпендикуляром, соединяющим два основания, и может быть проведена в любой их точке, но удобнее всего это делать из вершины углов при меньшем основании, так как тогда образуется прямоугольный треугольник, из которого выводится формула. (рис.103.1) h=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )

Средней линией трапеции называется отрезок, соединяющий середины боковых сторон, и равный полусумме оснований. (рис.103.2) m=(b+d)/2

Площадь трапеции равна произведению ее высоты на среднюю линию. Чтобы найти площадь трапеции через стороны, необходимо развернуть эту формулу до ее истоков, заменив неизвестные переменные. S=hm=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )*(b+d)/2

Если в трапецию можно вписать окружность (а это возможно, если противоположные стороны в сумме дают одно и то же число), то радиус вписанной окружности будет равен половине высоты, или половине квадратного корня из произведения меньшего основания на большее, с учетом условия для окружности. (рис.103.3) r=h/2=√bd/2

Описать окружность можно только вокруг равнобокой трапеции, и если она является таковой, то радиус описанной окружности будет равен радиусу окружности, описанной вокруг треугольника, образованного диагональю. (рис.103.4) R=(abd_1)/√((a+b+d_1)(a+b)(a+d_1)(b+d_1))

Диагонали трапеции рассчитываются по формулам, приведенным через теорему Пифагора в треугольниках, образованных высотой и диагоналями. d_1=√(c^2+db d(c^2-a^2 )/(d-b)) d_2=√(a^2+db (b(c^2-a^2))/(d-b))

Примеры вычисления площади треугольника

Для наглядности, рассмотрим применение формул на нескольких практических примерах:

Задача 1

Дано: трапеция с основаниями a=4см, b=8см и высотой h=5см. Как найти площадь трапеции? Берем формулу S= 1/2×(a+b)×h из первого примера и подставляем значения S= Ответ: 30 см2.

Задача 2

Дано: неравнобедренная трапеция с проведенными диагоналями x=12 см, y=17 см. Угол их пересечения равен 30. Необходимо рассчитать площадь. Для этого воспользуемся соответствующей формулой: S=1/2×d₁×d₂×sin(α). Из табличных значений мы знаем, что синус 30=1/2. Подставляем значения: Ответ: 51 см2.

Задача 3

Условия просты. Известна величина средней линии m=15 см и высота h=21 см. Перемножаем эти значения по формуле S=m×h . Ответ: площадь трапеции равна 315 см2.

Задача 4

Дано: верхнее основание трапеции a=5 см, нижнее b=15 см. Имеется вписанная окружность с радиусом r=2,5 см. Требуется вычислить площадь трапеции. Для этого применяем формулу S = r*(a+b)= 50 см2.

Задача 5

Имеется равнобедренная трапеция. Известны основания трапеции a=10 см, b=22 см. Угол, прилежащий к нижнему основанию равен 45. Необходимо вычислить площадь. Для этого подставляем значения в геометрическую формулу, приведенную в 8 методе: S = (b²-a²)*tg(α)/4=192 см2. Тангенс 45=1 (берется из табличных данных).

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°

Онлайн калькулятор

Через длины оснований и высоту

основание a = основание b = высота h =

Чему равна площадь трапеции если известны основания a и b, а также высота h?

Пример

Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:

S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²

Через среднюю линию и высоту

средняя линия m = высота h =

Чему равна площадь трапеции если известны средняя линия m и высота h?

Пример

Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:

Через длины сторон и оснований

основание a = основание b = сторона c = сторона d =

Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?

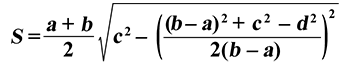
Пример

Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:

Через диагонали и угол между ними

Чему равна площадь трапеции если известны диагонали d₁ и d₂ и угол между ними α?

Пример

Если у трапеции одна диагональ d₁ = 5 см, другая диагональ d₂ = 7 см, а угол между ними ∠α = 30°, то её площадь:

S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²

Площадь равнобедренной трапеции

Через среднюю линию, боковую сторону и угол при основании

средняя линия m = сторона c = угол α =

Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?

Пример

Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:

S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²

Через радиус вписанной окружности

радиус r = угол α =

Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?

Пример

Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:

S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²

Базовые формулы для расчета площади трапеции

Формула 1: Площадь трапеции S может быть вычислена по формуле: S = (a + b) * h / 2, где a и b — основания трапеции, h — высота трапеции.

Формула 2: Часто используется формула S = [(a + b) / 2] * h, где все те же переменные.

Формула 3: Если известны длины всех сторон трапеции, S может быть вычислена с помощью формулы Герона: S = √, где p — полупериметр трапеции, равный (a+b+c)/2, а a, b и c — длины сторон трапеции.

Формула 4: Еще одна формула для расчета площади трапеции — S = (h/2) * , где все те же переменные.

Формула 5: Если известны угол и длины оснований трапеции, то S можно вычислить с помощью формулы S = / 4tan(α/2), где α — угол между основаниями трапеции.

Определение и свойства трапеции:

Трапеция — это четырехугольник, у которого две стороны (основания) параллельны. Основания называются верхней и нижней, а боковые стороны — боковыми ребрами.

В трапеции можно выделить несколько свойств:

Периметр трапеции равен сумме длин всех ее сторон. Для решения задачи, где требуется найти периметр трапеции, нужно сложить длины всех сторон.
Площадь трапеции можно найти по формуле: S = (a + b) * h / 2, где a и b — длины оснований, а h — высота трапеции, которая проведена между основаниями. Для решения задачи, где требуется найти площадь трапеции, нужно подставить известные значения в формулу и выполнить вычисления.
Трапеция может быть равнобокой, когда ее боковые стороны равны. Также существует равнобедренная трапеция, где основания равны, а боковые стороны — равны друг другу.
В трапеции диагонали делятся пополам. Это означает, что если в трапеции провести две диагонали, то они будут пересекаться в точке, которая делит каждую диагональ пополам.
Сумма углов трапеции равна 360 градусам. То есть, если измерить все углы трапеции и сложить их, получится значение 360 градусов.

Используя эти свойства, можно решить задачи, связанные с нахождением периметра и площади трапеции. Для этого нужно знать значения оснований, боковых сторон и высоты трапеции. Вычисления можно выполнить с помощью соответствующих формул.

Что такое трапеция?

Трапеция — это четырехугольник, у которого две стороны параллельны и называются основаниями. Остальные две стороны называются боковыми сторонами.

Трапеция имеет много свойств и особенностей. Одно из основных свойств трапеции — это то, что сумма длин ее двух оснований равна периметру.

Также в трапеции можно найти площадь. Для этого можно воспользоваться разными формулами, в зависимости от известных данных. Например, если известны длины оснований и высота трапеции, то площадь можно найти по формуле:

Площадь = (сумма длин оснований / 2) * высота.

Если известны длины оснований и угол между ними, то площадь можно найти по формуле:

Площадь = (сумма длин оснований / 2) * синус угла.

Задача на нахождение периметра трапеции по её основаниям и площади представляет собой поиск неизвестной длины боковых сторон. Для решения такой задачи можно использовать различные методы, например, систему уравнений или теорему Пифагора.

Какие свойства имеет трапеция?

Трапеция — это четырехугольник, у которого две стороны параллельны и называются основаниями. Остальные две стороны называются боковыми сторонами. Трапеция имеет следующие свойства:

Основания: Трапеция имеет два основания, которые являются параллельными отрезками.
Боковые стороны: У трапеции есть две боковые стороны, которые соединяют основания.
Углы: В трапеции существуют два параллельных угла, которые находятся на противоположных сторонах от оснований.

Трапеция может быть различных видов, в зависимости от своей геометрической формы:

Прямоугольная трапеция: У этого вида трапеции один из углов является прямым углом.
Равнобедренная трапеция: В этом типе трапеции две боковые стороны и два угла при основаниях равны между собой.
Произвольная трапеция: Это самый общий вид трапеции, который не имеет дополнительных ограничений на свою форму.

Задача по решению трапеции может быть различной: например, найти периметр или площадь. Периметр трапеции вычисляется как сумма длин всех её сторон, а площадь — как произведение полусуммы оснований на высоту.

❓Вопросы и ответы

При расчете площади трапеции могут возникать различные вопросы. Вот некоторые из наиболее частых вопросов и ответы на них:

Как найти высоту трапеции, если она неизвестна?

Высота трапеции является перпендикулярной линией, проведенной от одного основания до другого. Если вы не знаете высоту, но знаете длины оснований и площадь трапеции, то можно использовать формулу S = (a + b)h/2, где S — площадь, a и b — длины оснований, h — высота. Решая эту формулу относительно h, вы получите высоту трапеции: h = 2S / (a + b).

Как рассчитать площадь криволинейной трапеции?

Чтобы рассчитать площадь криволинейной трапеции, необходимо знать длины ее оснований и наклонных боковых сторон, а также высоту. Затем вы можете использовать формулу для площади трапеции: S = (a + b)h/2, где a и b — длины оснований, h — высота. Для криволинейной трапеции вместо a и b необходимо использовать длины соответствующих наклонных сторон.

Как проверить, что я правильно рассчитал площадь трапеции?

Вы можете проверить правильность своих расчетов, используя формулу для площади трапеции. Также вы можете использовать наш онлайн калькулятор площади трапеции, чтобы проверить свои расчеты. Если вы измерили длины сторон и углы трапеции с помощью инструментов, то также можете проверить свои измерения, сравнив их с теоретическими значениями.

Как решить задачу на поиск периметра трапеции по её основаниям и площади:

Для решения задачи на поиск периметра трапеции по её основаниям и площади следует использовать соответствующую формулу периметра и известные данные.

Дано:

Длина первого основания трапеции (a);
Длина второго основания трапеции (b);
Площадь трапеции (S).

Для нахождения периметра трапеции необходимо выполнить следующие шаги:

Найти высоту трапеции (h) по формуле h = S / ((a + b) / 2), где S — площадь трапеции.
Найти боковые стороны трапеции (с) по формуле c = √(h^2 + (b — a)^2), где h — высота трапеции, a и b — основания трапеции.
Найти периметр трапеции (P) по формуле P = a + b + 2c, где a и b — основания трапеции, c — боковая сторона трапеции.

Таким образом, чтобы решить задачу на поиск периметра трапеции по её основаниям и площади, нужно применить формулы для нахождения высоты, боковых сторон и периметра трапеции, в зависимости от известных данных.

Шаги решения задачи на поиск периметра трапеции

Для решения задачи на поиск периметра трапеции необходимо выполнить следующие шаги:

Определить данные, из которых можно вычислить периметр трапеции. В данном случае нам даны основания трапеции и ее площадь.
Найти длину бокового стороны трапеции. Для этого можно воспользоваться формулой площади трапеции: S = (a + b) * h / 2, где S — площадь трапеции, a и b — основания трапеции, h — высота трапеции.
Определить длины всех сторон трапеции. Для этого можно использовать теорему Пифагора или формулы для прямоугольных треугольников, составленных из сторон трапеции и высоты.
Найти сумму всех сторон трапеции. Для этого сложите длины всех сторон.
Вычислить периметр трапеции, сложив сумму всех сторон.

Итак, шаги решения задачи на поиск периметра трапеции сводятся к нахождению длин боковых сторон трапеции, нахождению суммы всех сторон и вычислению периметра. Последовательное выполнение этих шагов приведет к решению задачи.

Пример задачи с решением

Рассмотрим пример задачи, в которой нужно найти периметр трапеции по её основаниям и площади.

Условие задачи:

Дана трапеция с основаниями a = 6 см и b = 10 см. Известно, что площадь трапеции S = 36 см2. Найдите её периметр.

Решение:

Найдем высоту трапеции h. Для этого воспользуемся формулой площади трапеции: S = (a + b) * h / 2. Подставим известные значения: 36 = (6 + 10) * h / 2. Решим уравнение относительно h: 36 * 2 = 16 * h, 72 = 16 * h. Получаем h = 72 / 16 = 4.5 см.
Найдем боковые стороны трапеции. Для этого воспользуемся теоремой Пифагора. Рассмотрим прямоугольный треугольник, образованный боковым ребром трапеции, его высотой и основанием. По теореме Пифагора получаем: a2 = h2 + x2, где x — длина боковой стороны. Подставляем известные значения: 62 = 4.52 + x2, 36 = 20.25 + x2, x2 = 36 — 20.25, x2 = 15.75, x = √15.75 ≈ 3.97 см. Так как боковые стороны трапеции параллельны и равны по длине, то x = y ≈ 3.97 см.
Найдем периметр трапеции. Периметр трапеции равен сумме длин всех её сторон. Имеем: P = a + b + 2 * y. Подставляем известные значения: P = 6 + 10 + 2 * 3.97, P ≈ 23.94 см.

Итак, периметр трапеции составляет около 23.94 см.

Как рассчитать площадь четырехугольника

На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.

Через диагонали и угол между ними
Через стороны и противолежащие углы
Площадь вписанного четырехугольника в окружность
Площадь описанного четырехугольника около окружности через радиус
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы

Через диагонали и угол между ними

Формула для нахождения площади четырехугольников через диагонали и угол между ними:

d1, d2 — диагонали; α — угол между диагоналями.

Через стороны и противолежащие углы

Формула для нахождения площади четырехугольников через стороны и противолежащие углы:

p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.

Площадь вписанного четырехугольника в окружность

Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:

p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника.

Площадь описанного четырехугольника около окружности через радиус

Формула для нахождения площади описанного четырехугольника около окружности через радиус:

p — полупериметр четырехугольника; r — радиус вписанной окружности; a, b, c, d — стороны четырехугольника.