Как найти площадь треугольника: формулы, калькулятор онлайн

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°

Площадь треугольника

Площадь разностороннего треугольника

Вычисляем площадь треугольника без особенностей – все его стороны разные и все углы разные.

Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле “площадь треугольника через две стороны и угол между ними”:

Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:

Площадь равнобедренного треугольника

Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.

К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:

Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.

Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:

Площадь прямоугольного треугольника

Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:

Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе

Площадь прямоугольного треугольника, если в него вписана окружность:

Площадь равностороннего треугольника

Площадь равностороннего треугольника можно найти через радиус описанной окружности.

Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:

Площадь равностороннего треугольника, если известна сторона треугольника:

Площадь равностороннего треугольника, если известна высота треугольника:

❓Что такое калькулятор площади треугольника?

Калькулятор площади треугольника — это инструмент, предназначенный для вычисления площади данной фигуры на основе известных данных о ее сторонах и высоте. Этот инструмент полезен для учеников, студентов, инженеров и геометров, которые занимаются проектированием и измерением различных объектов, а также для тех, кто интересуется математикой.

Что такое площадь треугольника?

Площадь треугольника — это количество плоскостей, занимаемых этим многоугольником. Это основной параметр, позволяющий определить, сколько материала необходимо для создания фигуры, и какова его стоимость.

Есть несколько способов вычисления площади треугольника, в зависимости от доступных данных. Одним из наиболее распространенных методов является формула Герона, которая основана на знании длины всех трех сторон треугольника. Метод Герона был придуман греческим математиком Героном Александрийским еще в первом веке нашей эры. С учетом значительных достижений геометрического анализа, этот способ вычисления площади треугольника все еще широко применяется в современной математике. Формула Герона основана на делении треугольника на три меньших треугольника.:

S = √(p (p-a)(p-b)(p-c))где S — площадь треугольникаа,b,c — длины его сторонар — полупериметр:p = (a+b+c)/2

Этот метод удобен для вычисления площади треугольника с помощью калькулятора площади треугольника, так как он требует минимального количества информации о фигуре.

Кроме того, площадь треугольника можно вычислить, если известна его высота и одна из его сторон. В этом случае можно использовать формулу:

S = (½)*b*hгде S — площадь треугольникаb — длина его основанияh — высота, опущенная к основанию.

Также можно использовать формулу для произвольного треугольника, которая учитывает длины двух сторон и находит угол между ними:

S = (½)*a*b*(sinC)где S — площадь треугольникаa,b — длины сторонC — угол между ними

Для вычисления площади треугольника с помощью калькулятора площади треугольника, необходимо иметь известную длину хотя бы одной его стороны и высоту, опущенную к этой стороне.

Для равнобедренного треугольника

Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.

Через основание и сторону

В этом случае формула будет выглядеть следующим образом:

\(S=\frac b4\sqrt{4a^2-b^2}\)

где a — одно из боковых ребер фигуры, а b — ее основание.

Через основание и противолежащий угол

Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:

\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)

где b — основание многоугольника, β — противолежащий ему угол.

Через основание и высоту

Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:

\(S=\frac{b\times h}2\)

где b — основание фигуры, а h — высота, проведенная к этому основанию.

Через боковые стороны и угол между ними

Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:

\(S=\frac12a^2\times\sin\left(\beta\right)\)

где a — это боковое ребро, β — угол между равными ребрами.

Через основание и угол между боковыми сторонами

В этом случае нам сначала придется найти высоту по формуле:

\(h=\frac b2\tan\left(\beta\right)\)

где β — угол при вершине, а b — основание.

Далее подставляем значение в формулу

\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)

Итоговая формула:

\(S=frac{b^2\tan\left(\beta\right)}4\)

Площадь треугольника по основанию и высоте

Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):

Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

Доказательство. Пусть AC основание треугольника ABC (Рис.2).

Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку \( \small AC \ || \ BD \) и \( \small AB\ || \ CD \), то ABDC является параллелограммой и, следовательно, \( \small AC \ = \ BD \), \( \small AB\ = \ CD . \) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна \( \small S_=AC \cdot BH, \) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

Обозначим через k отношение

То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Нахождение площади треугольника по трём сторонам: онлайн-калькулятор

Рассчитать площадь треугольника формулой по трем сторонам онлайн-калькулятором пригодится школьникам, студентам, преподавателям, специалистам различных специальностей. Вычисления производятся бесплатно. Пользователь сервиса получает не только готовый ответ, но и подробное решение. Используя данный способ, можно осуществлять самостоятельную подготовку к занятиям без привлечения репетиторов.

Чтобы найти площадь треугольника по трем сторонам онлайн:

введите данные длины сторон треугольника в соответствующие поля;
выберите единицы измерения для каждой стороны и для предполагаемой площади треугольника;
для получения ответа нажмите кнопку «Рассчитать».

В автоматических вычислениях заложена формула Герона, в которой фигурируют величины трех сторон треугольника и его полупериметра.

Примеры

1. Найдите площадь треугольника, если две его стороны равны 6 см и 12 см, а угол между этими сторонами равен 30 градусов.

Решение:

\(S= 0,5 *a*b*sin \alpha= 0,5*6*12*sin30 = 18\) (Ответ 18 см2)

2. Найдите площадь треугольника, если высота равна 4 см. , а основание равно 8 см.

Решение:

\(S = {{a*h} \over 2} = {{8*4} \over 2} = 16\) (Ответ 16 см2)

3. Треугольник вписан в окружность радиусом 10см. Длины сторон треугольника 8 см, 6 см и 4 см. Найдите площадь вписанного треугольника со сторонами, равными этим числам, зная радиус описанной окружности.

Решение:

\(S = \frac{a*b*c}{4R} = \frac{8*6*4}{4*10} = 4,8\)

Для прямоугольного треугольника

В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.

По двум сторонам

Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:

\(S=\frac{a\times b}2\)

где a и b — катеты прямоугольного треугольника.

Через гипотенузу и острый угол

Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.

Начнем с поиска катета:

\(\cos\left(\alpha\right)=\frac ac\)

\(a=c\times\cos\left(\alpha\right)\)

где c — гипотенуза треугольника, a — его катет, а α —угол между ними.

Подставляем получившееся значение в формулу \(S=\frac12a\times c\times\sin\alpha\), получается:

\(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\)

Через катет и прилежащий угол

В этом случае нужно будет использовать следующую формулу:

\(S=\frac12\times a^2\times\tan\left(\alpha\right)\)

Через радиус вписанной окружности и гипотенузу

Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:

\(S=r\times(r+c)\)

где r — радиус вписанной окружности, c — гипотенуза.

Через вписанную окружность

Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:

\(S=с_1\times с_2\)

где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.

По формуле Герона

Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:

\(S=(p-a)\times(p-b)\)

где \(p=\frac{a+b+c}2\) — полупериметр фигуры.

Информация по назначению калькулятора

Треугольник — это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.

В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.

Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.

Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:

⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° — это правильный многоугольник.

⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник — это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.

⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.

Треугольники также могут быть классифицированы в соответствии с их внутренними углами:

⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны — катеты треугольника.

⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).

⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник — это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.

⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.

Онлайн калькулятор поможет найти параметры треугольника, такие как:

Длины сторон — равны в равностороннем треугольнике
Углы — также равны в равностороннем треугольнике
Высота — это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
Периметр — равен сумме всех 3х сторон ()
Площадь — равна половине произведения высоты и стороны к которой построена высота ()
Медианы
Биссектрисы
Радиус Вписанной и Описанной окружностей
Диаметр Вписанной и Описанной окружностей
Длина Вписанной и Описанной окружностей
Площадь Вписанной и Описанной окружностей

Формула площади треугольника через две стороны и угол между ними

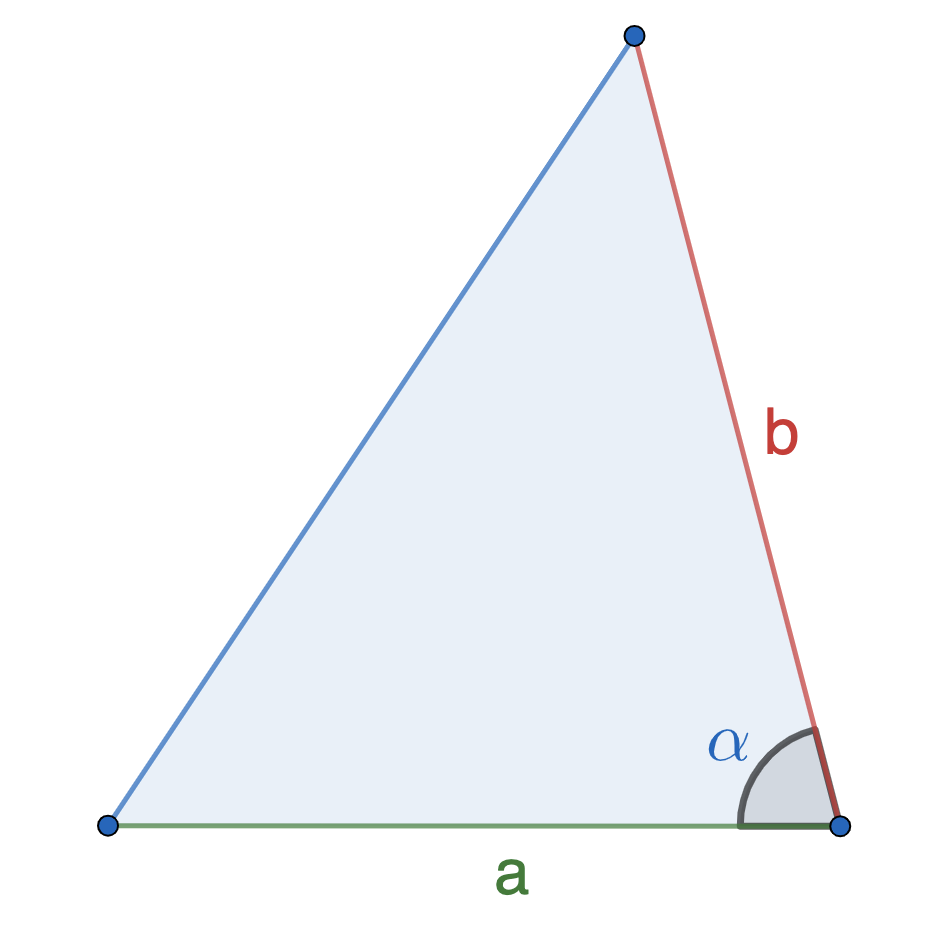
\(S = 0,5*a*b*sin\alpha\)

a, b — стороны, прилежащие к углу \(\alpha\)

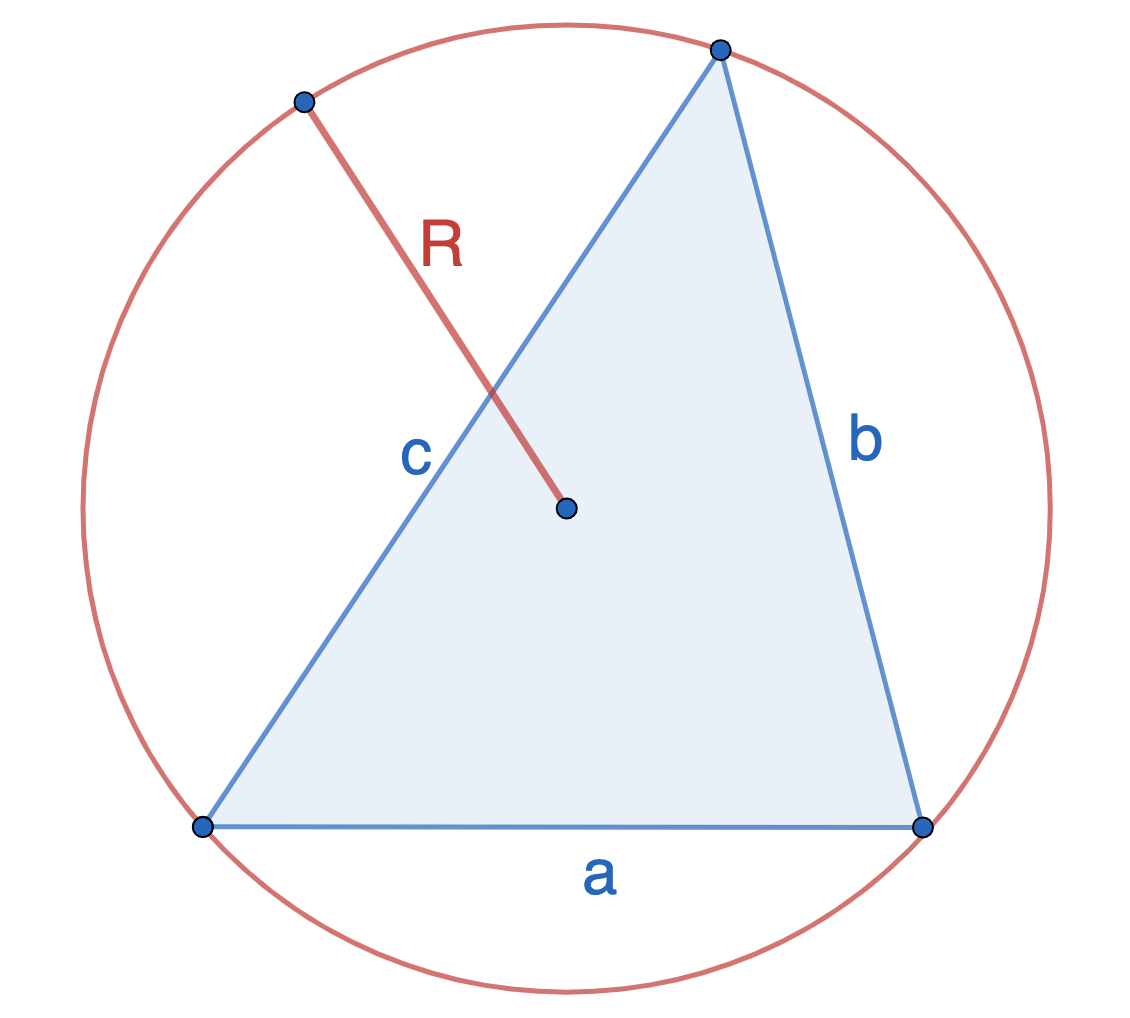
\(S = \frac{a*b*c}{4R}\)

\(R\) — радиус описанной окружности

\(a, b, c\) — длины сторон треугольника

Примеры

Решение:

\(S= 0,5 *a*b*sin \alpha= 0,5*6*12*sin30 = 18\) (Ответ 18 см2)

2. Найдите площадь треугольника, если высота равна 4 см. , а основание равно 8 см.

Решение:

\(S = {{a*h} \over 2} = {{8*4} \over 2} = 16\) (Ответ 16 см2)

Решение:

Формула площади треугольника через три стороны и описанную окружность

\(S = \frac{a*b*c}{4R}\)

\(R\) — радиус описанной окружности

\(a, b, c\) — длины сторон треугольника

Примеры

Решение:

\(S= 0,5 *a*b*sin \alpha= 0,5*6*12*sin30 = 18\) (Ответ 18 см2)

2. Найдите площадь треугольника, если высота равна 4 см. , а основание равно 8 см.

Решение:

\(S = {{a*h} \over 2} = {{8*4} \over 2} = 16\) (Ответ 16 см2)

Решение:

Найти площадь треугольника

Ввод данных в калькулятор для вычисления площади треугольника

В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.

Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Вы можете найти площадь треугольника если знаете следующие параметры:

Длины трех сторон (используя формулу Герона)
Длины двух сторон и значение угла между ними
Длины стороны и опущенной на нее высоты
Длины трех сторон и радиус описанной окружности
Длины трех сторон и радиус вписанной окружности
Длина полупериметра и радиус вписанной окружности
Длина двух сторон и одного угла треугольника
Длина одной стороны и двух углов треугольника
Радиус описанной окружности и два угла треугольника

Как рассчитывается площадь треугольника?

Площадь треугольника может быть рассчитана на основе формулы, зависящей от известных параметров треугольника. Существуют несколько различных формул для расчета площади треугольника, которые можно использовать в зависимости от того, какие параметры известны.

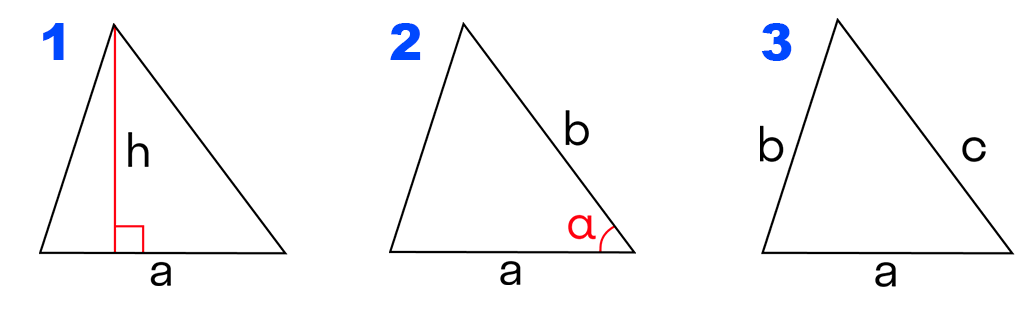
Формула 1. Через длину основания и высоту, опущенную на это основание:

Формула 2. Через две стороны и угол между ними:

где α — угол между сторонами а и b

Формула 3. Формула Герона через 3 стороны:

где p = (a+b+c)/2 – полупериметр.

Во всех формулах S обозначает площадь треугольника, b обозначает длину основания прямоугольного треугольника, h обозначает высоту, a, b, и c обозначают длины сторон непрямоугольного треугольника, x и y обозначают координаты вершин треугольника.

Рассчитывая площадь треугольника, важно использовать правильную формулу в зависимости от известных параметров, чтобы получить правильный ответ

Как использовать калькулятор?

Использовать калькулятор площади треугольника довольно просто. Вот общие шаги, которые необходимо выполнить для использования калькулятора:

Откройте калькулятор площади треугольника в своем браузере. Вы можете найти онлайн-калькуляторы площади треугольника на многих сайтах, которые предоставляют подобные сервисы, в том числе и на нашем.
Введите параметры треугольника, которые известны вам. В зависимости от конкретного калькулятора вы можете вводить длины сторон, длину основания и высоту, координаты вершин на плоскости и т.д.
Нажмите на кнопку «Рассчитать» или «Вычислить». Калькулятор площади треугольника обычно автоматически рассчитывает площадь на основе введенных параметров и выдает результат.
Прочитайте результат. Калькулятор площади треугольника может выдавать результат в разных форматах, например, в виде числа или дроби. Если вы хотите, чтобы результат был точнее, можете использовать калькулятор с более высокой точностью.
Сбросьте введенные данные и повторите расчет, если нужно. Если вам нужно рассчитать площадь треугольника с другими параметрами, то можете сбросить предыдущие данные и ввести новые параметры.

В целом, использование калькулятора площади треугольника довольно просто и позволяет быстро и точно рассчитать площадь треугольника на основе его параметров.

Вопросы и ответы

Также полезно ознакомиться с ответами на часто задаваемые вопросы по данному вопросу.

Как использовать калькулятор площади треугольника?

Для использования калькулятора площади треугольника нужно ввести известные параметры треугольника, такие как длины сторон, длина основания и высота, координаты вершин на плоскости и т.д., а затем нажать на кнопку «Рассчитать» или «Вычислить». Калькулятор автоматически рассчитывает площадь треугольника и выводит результат.

Какой формулой рассчитывается площадь треугольника?

Площадь треугольника можно рассчитать с помощью формулы: S = (a * h) / 2, где S – площадь треугольника, a – длина основания, h – высота, опущенная на основание.

Где можно найти онлайн-калькулятор площади треугольника?

Онлайн-калькуляторы площади треугольника можно найти на многих сайтах, которые предоставляют подобные сервисы. Также можно использовать калькуляторы научных порталов или мобильные приложения.

Какие единицы измерения используются в калькуляторе площади треугольника?

Калькулятор площади треугольника может использовать разные единицы измерения, например, метры, сантиметры, дюймы, футы и т.д. Обычно единицы измерения выбираются в соответствии с системой измерений, используемой в конкретной стране или регионе.

Можно ли использовать калькулятор площади треугольника для расчета площади других фигур?

Нет, калькулятор площади треугольника предназначен только для расчета площади треугольников. Для расчета площади других геометрических фигур необходимо использовать другие калькуляторы, например, калькуляторы площади круга, прямоугольника и т.д.

Как работает калькулятор площади треугольника?

Работа калькулятора площади треугольника может немного отличаться в зависимости от конкретного онлайн-инструмента, но обычно он использует формулу для расчета площади треугольника на основе заданных параметров.

Если треугольник является прямоугольным, то для расчета его площади необходимо знать длину основания и высоту, которая опускается на это основание. А если треугольник непрямоугольный, то для расчета его площади необходимо знать длины всех трех сторон.

Калькулятор площади треугольника может использовать эти формулы для расчета площади, если пользователь введет необходимые параметры (например, длины сторон или длину основания и высоту). Результат может быть выдан в виде числа или дроби в зависимости от точности калькулятора.

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Формула Герона для нахождения площади треугольника:

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Формула нахождения площади треугольника через две стороны и угол между ними:

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Формула нахождения площади прямоугольного треугольника через катеты:

Формула нахождения площади равнобедренного треугольника через две стороны:

Формула нахождения площади равнобедренного треугольника через основание и угол:

Формула нахождения площади равностороннего треугольника через сторону:

Формула нахождения площади равностороннего треугольника через высоту:

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

📚Частые вопросы про площадь треугольника

Площадь треугольника – это количество плоских единиц, заключенных внутри его границ. Вычислить площадь треугольника можно различными способами, в зависимости от имеющихся данных и требуемой точности. Ниже рассмотрим наиболее часто встречающиеся вопросы про площадь треугольника.

Как вычислить площадь треугольника по формуле?

Формула для вычисления площади треугольника звучит так:

S = ½ * a * hгде S – площадь треугольникаa – основание треугольникаh – высота, проведенная к основанию.Для примера, площадь треугольника с основанием 10 см и высотой 6 см равна:S = ½ * 10 * 6 = 30 кв. см.

Как вычислить площадь треугольника по формуле Герона?

Формула Герона – это более сложный способ вычисления площади треугольника, основанный на длинах его сторон.

Для этого нужно использовать формулу:

S = √p (p-a)(p-b)(p-c)где S – площадь треугольникаa, b и c – длины сторонp – полупериметр, или p = (a+b+c)/2Например, пусть треугольник ABC имеет стороны длины 5, 6 и 7 единиц. Его полупериметр равен:p = (5+6+7)/2 = 9 единиц.Тогда вычисляем его площадь:S = √9 (9-5)(9-6)(9-7)≈7.48 квадратных единиц.

Как вычислить площадь треугольника по координатам вершин?

Если известны координаты вершин треугольника, то его площадь можно вычислить по формуле:

S = ½ |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)|где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника в порядке обхода по часовой стрелке или против часовой стрелки, а | | обозначает модуль числа.Например, пусть треугольник имеет вершины A (1, 2), B (3, 4) и C (5, 7). Тогда его площадь равна:S = ½ |1 (4 – 7) + 3 (7 – 2) + 5 (2 – 4)| = 4.5 квадратных единиц.

Как вычислить площадь треугольника, если известны длины двух сторон и угол между ними?

Если известны длины двух сторон треугольника и угол между ними, то его площадь можно вычислить по формуле:

S = ½ absin (α)где a и b – длины сторон треугольникаα – угол между ними а sin (α) – синус этого угла.Например, пусть треугольник имеет стороны длинной 6 и 8 единиц, а между ними угол в 60 градусов. Тогда его площадь равна:S = ½ 6 * 8 * sin (60)≈ 13.86 квадратных единиц.

Вопросы про площадь треугольника могут быть различными, но решение их можно найти, используя соответствующие формулы и данные. Если же точных данных нет, то можно использовать приближенные методы вычисления площади треугольника.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.

Формула расчета

2. Через длину трех сторон (формула Герона)

Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).

Формула расчета:

p – полупериметр, который считается так:

3. Через две стороны и угол между ними

Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).

Теория. Площадь треугольника

Формули площади треугольника

Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

S = 1 a · h

2
Формула площади треугольника по трем сторонам

Формула Герона

Формула площади треугольника по двум сторонам и углу между нимиПлощадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S =	1	a · b · sin γ
2

Формула площади треугольника по трем сторонам и радиусу описанной окружности

S =	a · b · с
4R

Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b , r — радиус вписанной окружности, R — радиус описанной окружности, p — полупериметр треугольника.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Как найти площадь треугольника

Формула Герона для нахождения площади треугольника:

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Формула нахождения площади треугольника через две стороны и угол между ними:

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Формула нахождения площади прямоугольного треугольника через катеты:

Формула нахождения площади равнобедренного треугольника через две стороны:

Формула нахождения площади равнобедренного треугольника через основание и угол:

Формула нахождения площади равностороннего треугольника через сторону:

Формула нахождения площади равностороннего треугольника через высоту:

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Примеры решения задач

Разберемся с нахождением площади треугольника наглядно на примере некоторых случаев.

Задача 1

В треугольник вписана окружность с радиусом 6 см. Известно, что его стороны равны 10 см, 12 см и 14 см. Определить площадь фигуры.

Решение

Для расчета будем использовать формулу \(S=r\times\frac{a+b+c}2\) или \(S=r\times p\). Подставляем имеющиеся значения и получается:

\(S=6\times\frac{10+12+14}2=6\times18=108\) \(см^2\)

Ответ: \(108\) \(см^2\).

Задача 2

Дан равносторонний треугольник, вокруг которого описали окружность с радиусом 3 см. Посчитать S данной фигуры.

Решение

Считать будем, опираясь на следующее уравнение \(S=\frac{3\sqrt3R^2}4\). Подставляем данные величины и получаем:

\(S=\frac{3\sqrt33^2}4=\frac{27\sqrt3}4 см^2\)

Ответ: \(\frac{27\sqrt3}4 см^2.\)

Задача 3

Известно, что у равнобедренного треугольника основание равно 4 см, а стороны по 3 см. Нужно вычислить площадь фигуры.

Решение

Для расчета S используем формулу \(S=\frac b4\sqrt{4a^2-b^2}\). Получается:

\(\frac44\sqrt{4\times3^2-4^2}=\sqrt{36-16}=\sqrt{20}=2\sqrt5 см^2\)

Ответ: \(2\sqrt5 см^2.\)

Задача 4

Дан треугольник с прямым углом, у которого гипотенузы равна 2 см, а один из острых углов равен \(30^\circ\). Узнать S данной фигуры.

Решение

Для расчетов будем ориентировать на следующее уравнение: \(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\). Подставляем известные значения:

\(S=2^2\times\frac{\sqrt3}2\times\frac12=\sqrt3 см^2\)

Калькулятор площади для равнобедренных треугольников

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.

Площадь равнобедренного треугольника по боковым сторонам и основанию — калькулятор:

Формула	Результат
S = ¼ × c × √ (4 × a² — c²)
	Сторона a (a = b)
Сторона c

Если известны боковые стороны и угол между ними, то площадь равнобедренного треугольника определяется, как половина произведения квадрата боковой стороны на синус угла между боковыми сторонами.

Площадь равнобедренного треугольника по боковым сторонам и углу между ними:

Формула	Результат
S = ½ × a² × sin (α)
	Боковая сторона a (a = b)
Угол α° между боковыми сторонами

Если известна боковая сторона, основание и углу между ними, то площадь равнобедренного треугольника равна половине произведения боковой стороны и основания на синус угла между ними.

Площадь равнобедренного треугольника по боковой стороне, основанию и углу между ними — расчет:

Формула	Результат
S = ½ ×a × c × sin (β)
	Боковая сторона a (a = b)
Основание треугольника c
Угол β° между основанием и стороной

Если известно основание и угол между боковыми сторонами, то площадь равнобедренного треугольника рассчитывается, как четверть отношения квадрата основания на тангенс половинного угла между боковыми сторонами.

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами — онлайн:

Формула	Результат
S = c² ⁄ (4 × tg (½ × α))
	Основание треугольника c
Угол α° между боковыми сторонами

Площадь равнобедренного треугольника по высоте и основанию — калькулятор:

Формула	Результат
S = ½ × c × h
	Основание треугольника c
Высота h

Площадь треугольника — калькуляторы для всех видов

Площадь треугольника

Площадь разностороннего треугольника

Площадь равнобедренного треугольника

Площадь прямоугольного треугольника

Площадь равностороннего треугольника

❓Что такое калькулятор площади треугольника?

Что такое площадь треугольника?

Для равнобедренного треугольника

Через основание и сторону

Через основание и противолежащий угол

Через основание и высоту

Через боковые стороны и угол между ними

Через основание и угол между боковыми сторонами

Площадь треугольника по основанию и высоте

Нахождение площади треугольника по трём сторонам: онлайн-калькулятор

Примеры

Для прямоугольного треугольника

По двум сторонам

Через гипотенузу и острый угол

Через катет и прилежащий угол

Через радиус вписанной окружности и гипотенузу

Через вписанную окружность

По формуле Герона

Информация по назначению калькулятора

Онлайн калькулятор поможет найти параметры треугольника, такие как:

Формула площади треугольника через две стороны и угол между ними

Примеры

Формула площади треугольника через три стороны и описанную окружность

Примеры

Найти площадь треугольника

Ввод данных в калькулятор для вычисления площади треугольника

Вы можете найти площадь треугольника если знаете следующие параметры:

Как рассчитывается площадь треугольника?

Как использовать калькулятор?

Вопросы и ответы

Как использовать калькулятор площади треугольника?

Какой формулой рассчитывается площадь треугольника?

Где можно найти онлайн-калькулятор площади треугольника?

Какие единицы измерения используются в калькуляторе площади треугольника?

Можно ли использовать калькулятор площади треугольника для расчета площади других фигур?

Похожие калькуляторы

Как работает калькулятор площади треугольника?

Как найти площадь треугольника

📚Частые вопросы про площадь треугольника

Как вычислить площадь треугольника по формуле?

Как вычислить площадь треугольника по формуле Герона?

Как вычислить площадь треугольника по координатам вершин?

Как вычислить площадь треугольника, если известны длины двух сторон и угол между ними?

Расчет площади

2. Через длину трех сторон (формула Герона)

3. Через две стороны и угол между ними

Похожие калькуляторы

Теория. Площадь треугольника

Формули площади треугольника

Формула Герона

Как найти площадь треугольника

Примеры решения задач

Задача 1

Задача 2

Задача 3

Задача 4

Калькулятор площади для равнобедренных треугольников

Похожие записи:

Похожие записи: