Что такое отрезок в геометрии

Введение

Мы на­чи­на­ем изу­че­ние гео­мет­рии. Это древ­няя наука, воз­ник­ла еще за 300 лет до нашей эры. В пе­ре­во­де с гре­че­ско­го «гео­мет­рия» – «зем­ле­ме­рие», изу­ча­ет она гео­мет­ри­че­ские фи­гу­ры и их свой­ства.

Под­раз­де­ля­ет­ся на два боль­ших раз­де­ла:

— пла­ни­мет­рия – гео­мет­рия на плос­ко­сти,

— сте­рео­мет­рия – гео­мет­рия в про­стран­стве.

При­ме­ры плос­ких фигур – тре­уголь­ник, окруж­ность и т.д. Мы с ними зна­ко­мы.

Мы зна­ко­мы и с про­стран­ствен­ны­ми фи­гу­ра­ми – шар, куб, па­рал­ле­ле­пи­пед и т.д., т.е. гео­мет­рия – во­круг нас.

Мы ска­за­ли, что гео­мет­рия изу­ча­ет свой­ства гео­мет­ри­че­ских фигур.

А что такое гео­мет­ри­че­ская фи­гу­ра? Это любое мно­же­ство, любая со­во­куп­ность точек.

Точки обо­зна­ча­ют боль­ши­ми ла­тин­ски­ми бук­ва­ми.

По­ня­тие о пря­мой дает тон­кая нить, про­дол­жен­ная бес­ко­неч­но в обе сто­ро­ны.

Точка и пря­мая – это неопре­де­ли­мое из­на­чаль­ное по­ня­тие, это ма­те­ма­ти­че­ская иде­а­ли­за­ция – раз­ме­ров они не имеют.

Если точки обо­зна­ча­ют­ся боль­ши­ми бук­ва­ми, то пря­мая может обо­зна­чать­ся ма­лень­ки­ми ла­тин­ски­ми бук­ва­ми.

Об­ри­су­ем в общих чер­тах, как стро­ит­ся гео­мет­рия. Мы упо­мя­ну­ли два по­ня­тия: точка, пря­мая . Это из­на­чаль­ные неопре­де­ли­мые по­ня­тия, их свой­ства вы­ра­жа­ют­ся в ак­си­о­мах, т.е. в ис­ти­нах, ко­то­рые не тре­бу­ют до­ка­за­тельств.

Опре­де­ле­ние дру­гих фигур, на­при­мер, окруж­но­сти, шара и т.д., до­ка­зы­ва­ют­ся тео­ре­ма­ми, таким об­ра­зом, изу­ча­ют­ся свой­ства гео­мет­ри­че­ских фигур. Итак, все гран­ди­оз­ное зда­ние гео­мет­рии ба­зи­ру­ет­ся, во-пер­вых, на неопре­де­лен­ных по­ня­ти­ях, во-вто­рых, на ак­си­о­мах.

Да­вай­те сфор­му­ли­ру­ем три важ­ней­шие ак­си­о­мы, ко­то­рые ха­рак­те­ри­зу­ют вза­им­ное рас­по­ло­же­ние точек и пря­мых и рас­смот­рим их.

Узоры древности

Интерес человека к прямым и искривленным линиям можно отследить с древнейших времен. Самые разные кривые мы видим в геометрических узорах на керамике и в архитектуре. Кроме достаточно простых узоров, составленных из прямых линий, часто можно встретить и что-то более сложное: спирали, волнистые линии и другие.

Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца

Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку

Математика. 5 класс

Конспект урока

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок. Отрезком называют часть прямой между двумя точками

Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

• Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
• Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
• Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
• Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

1) а – это прямая.

2) АВ – это отрезок.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Взаимосвязь координат векторов и его начала и конца

На координатной плоскости любые две точки можно соединить друг с другом. В результате получается отрезок. Если же дополнительно указано, какая из этих точек – начало отрезка, а какая – конец, то в итоге мы уже имеем вектор. Попробуем определить, есть ли связь между координатами вектора и координатами (можно использовать сокращение коор-ты) его граничных точек.

Пусть в прямоугольной системе координат отмечены точки А (х_А;у_А) и В(х_B;у_B).Тогда можно задать вектор АВ. Также построим ещё два вспомогательных вектора ОА и ОВ, начинающиеся в точке О – начале коор-т:

Вектора ОВ и ОА – это радиус-векторы (так как их начало находится в начале координат), поэтому их коор-ты ОВ и ОА совпадают с коор-тами их концов (В и А соответственно):

Итак, зная коор-ты граничных точек вектора, можно найти и координаты данного вектора:

Например, если вектор начинается в точке А (2; 1), а заканчивается в точке В (6; 3), то коор-ты вектора АВ можно определить так:

Задание. Начало вектора находится в точке М, а конец – в точке К. Определите его коор-ты, если:

Решение. Из коор-т К мы просто вычитаем соответствующие коор-ты М, и в итоге определяем коор-ты вектора:

Задание. От точки H (8; 15) отложили вектор m. Каковы координаты конца этого вектора?

Решение. Обозначим интересующие нас коор-ты как (х_к; у_к). Для вектора, начинающегося в точке (8; 15) и заканчивающегося в точке (х_к; у_к), коор-ты можно вычислить так:

Однако нам даны координаты вектора, то есть величины х и у, поэтому мы можем записать:

Оба равенства представляет собой уравнения, которые можно решить:

В итоге получили, что конец вектора находится в точке (13; 9).

Направленный отрезок — это вектор

Сегменты бывают двух типов:

1. Ненаправленного.
2. Режиссер.

Для ненаправленных сегментов AB и BA — это одни и те же сегменты, поскольку направление не имеет значения.

Если мы говорим об направленных отрезках, порядок перечисления концов имеет решающее значение. В этом случае AB➜ и BA➜ — разные отрезки, так как они противоположно направлены.

Направленные отрезки называются векторами. Векторы могут обозначаться либо двумя прописными буквами латинского алфавита со стрелкой над ними, либо строчной буквой со стрелкой.

Модуль вектора — это длина направленного отрезка. Обозначается как AB➜. Модули векторов AB➜ и BA➜ равны.

Векторы часто рассматриваются в системе координат. Модуль вектора равен квадратному корню из суммы квадратов координат концов вектора.

Коллинеарные векторы — это те, которые лежат на одной или параллельных прямых.

Презентация на тему: » Теорема Длина отрезка, соединяющего концы ломаной, не превосходит длины самой ломаной. Доказательство. Рассмотрим, например, ломаную ABCDE. Заменим соседние.» — Транскрипт:

1

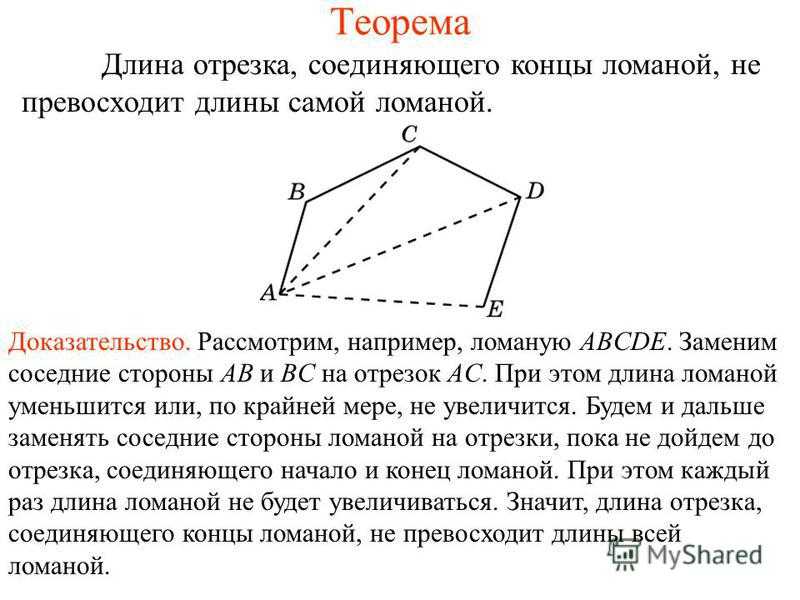
Теорема Длина отрезка, соединяющего концы ломаной, не превосходит длины самой ломаной. Доказательство. Рассмотрим, например, ломаную ABCDE. Заменим соседние стороны AB и BC на отрезок AC. При этом длина ломаной уменьшится или, по крайней мере, не увеличится. Будем и дальше заменять соседние стороны ломаной на отрезки, пока не дойдем до отрезка, соединяющего начало и конец ломаной. При этом каждый раз длина ломаной не будет увеличиваться. Значит, длина отрезка, соединяющего концы ломаной, не превосходит длины всей ломаной.

2

Упражнение 1 Ответ: 4 см. Для точек А, В, С, D на плоскости выполняются равенства АВ = 3 см, ВС = 4 см, CD = 5 см и неравенство AC + BD 2 см. Найдите AD.

3

Упражнение 2 Ответ: а) 8, 2; б) 8, 5; в) 8, 1. На рисунке изображены стержни, соединенные шарнирами, которые могут свободно двигаться. Для каждой конструкции найдите наибольшее и наименьшее расстояния, на которые можно раздвинуть концы A и B.

4

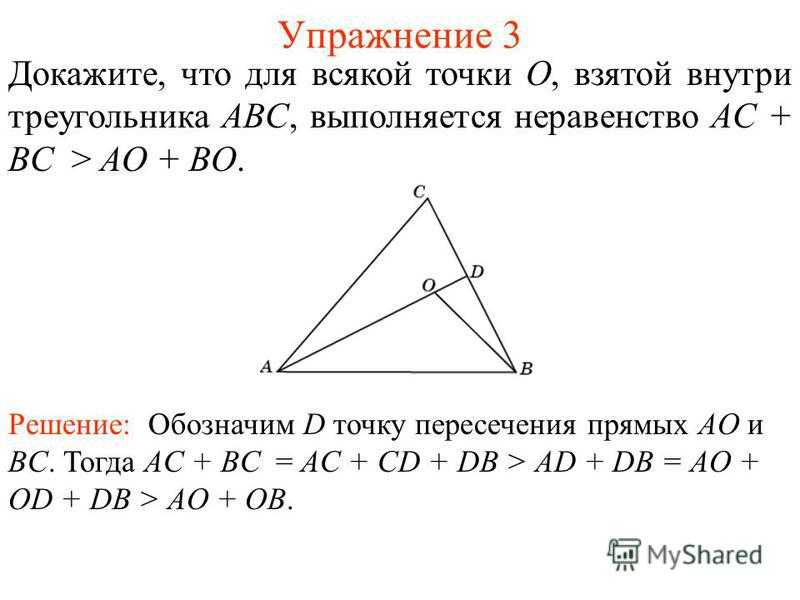
Упражнение 3 Докажите, что для всякой точки O, взятой внутри треугольника ABC, выполняется неравенство AC + BC > AO + BO. Решение: Обозначим D точку пересечения прямых AO и BC. Тогда AC + BC = AC + CD + DB > AD + DB = AO + OD + DB > AO + OB.

5

Упражнение 4 Докажите, что сумма расстояний от любой внутренней точки треугольника до его вершин меньше периметра треугольника и больше его полупериметра. Решение: Имеем неравенства AB

6

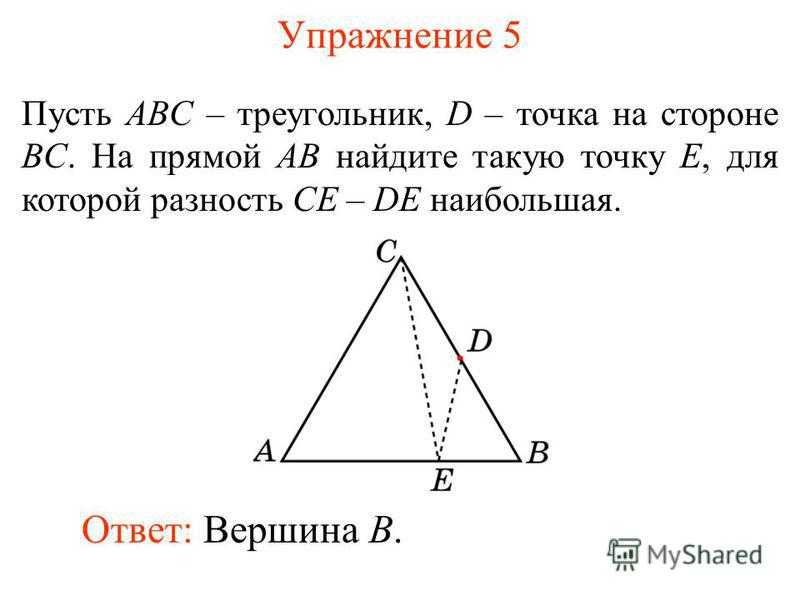
Упражнение 5 Пусть ABC – треугольник, D – точка на стороне BC. На прямой AB найдите такую точку E, для которой разность CE – DE наибольшая. Ответ: Вершина B.

7

Упражнение 6 Внутри выпуклого четырехугольника ABCD найдите точку O, сумма расстояний от которой до вершин четырехугольника наименьшая. Ответ: Точка пересечения диагоналей. Для любой другой точки O сумма расстояний от нее до вершин будет больше.

8

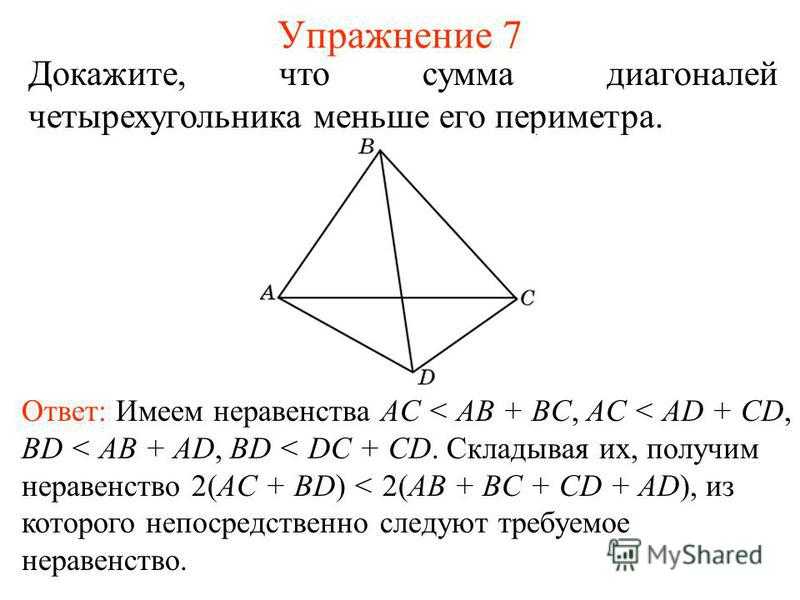
Упражнение 7 Докажите, что сумма диагоналей четырехугольника меньше его периметра. Ответ: Имеем неравенства AС

9

Упражнение 8 Докажите, что сумма диагоналей выпуклого четырехугольника больше его полупериметра. Ответ: Пусть O – точка пересечения диагоналей выпуклого четырехугольника ABCD. Имеем неравенства AO > AB – OB, BO > BC – OC, CO > CD – OD, DO > AD – OD,. Складывая их, получим неравенство 2(AC + BD) > AB + BC + CD + AD, из которого непосредственно следуют требуемое неравенство.

10

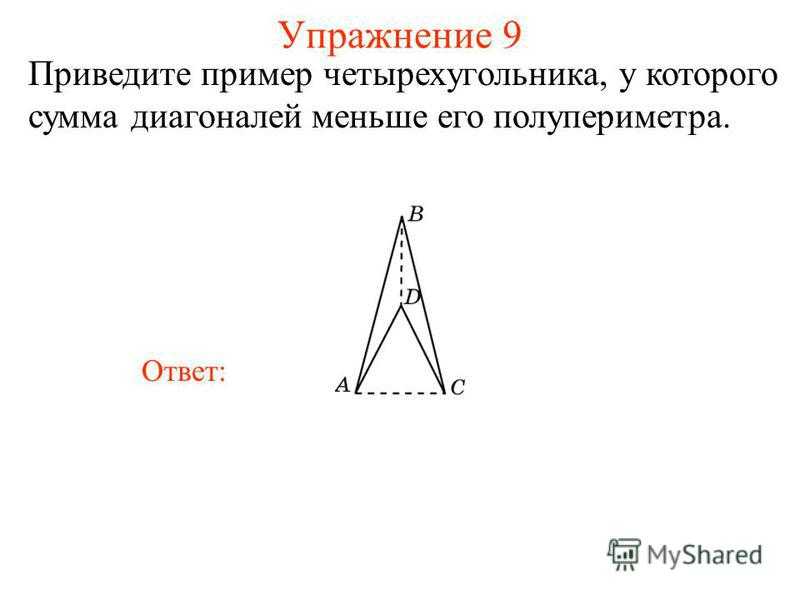
Упражнение 9 Приведите пример четырехугольника, у которого сумма диагоналей меньше его полупериметра. Ответ:

11

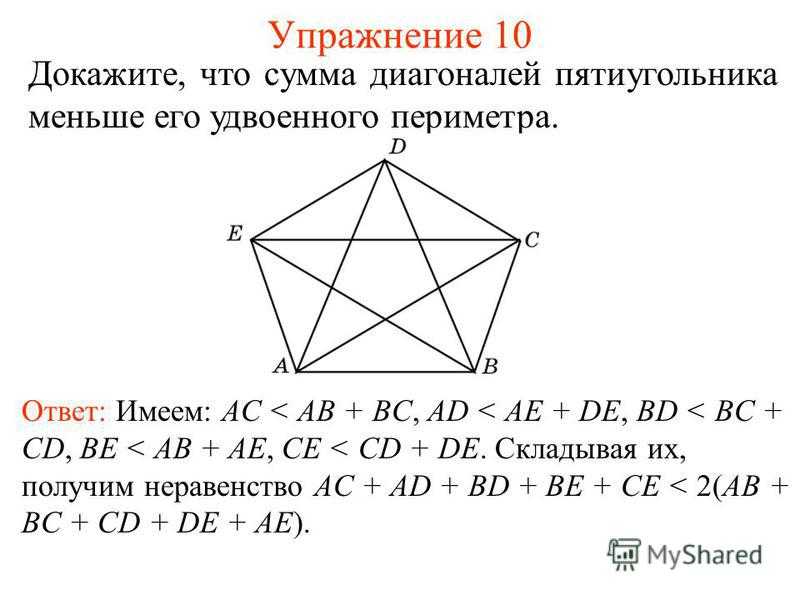
Упражнение 10 Докажите, что сумма диагоналей пятиугольника меньше его удвоенного периметра. Ответ: Имеем: AС

12

Упражнение 12 Сравните длины ломаных на рисунке, не измеряя их. Ответ: AB 1 C

13

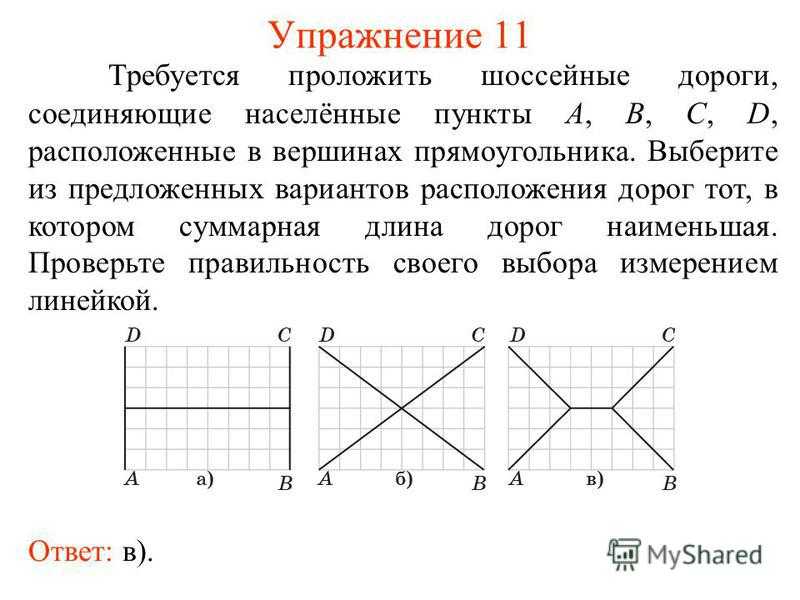
Упражнение 11 Требуется проложить шоссейные дороги, соединяющие населённые пункты A, B, C, D, расположенные в вершинах прямоугольника. Выберите из предложенных вариантов расположения дорог тот, в котором суммарная длина дорог наименьшая. Проверьте правильность своего выбора измерением линейкой. Ответ: в).

Вторжение иррационального

Кстати, даже в случае отрезков и прямых линий уже у греков возникли определенные проблемы. Давайте пройдем этот путь вместе с ними. Возьмем квадрат со стороной 1. Нетрудно посчитать, используя теорему Пифагора, что его диагональ будет равна корню из двух. Мы моментально попадаем в неловкую ситуацию: корень из двух (как мы знаем сейчас) — число иррациональное, а это значит, что если вы уменьшите сторону квадрата в целое число раз, то из полученных отрезков не сможете получить его диагональ: будет либо чуть больше, либо чуть меньше. Можно было бы сослаться здесь на неточность вычислений или измерений, но пифагорейцы получили этот результат вовсе не на практике, а из теоретических соображений. Доказательство их выглядело следующим образом:

Для пифагорейцев это была печальная новость — в рамках арифметики им такие числа не встречались, поэтому казалось, что и в целом вычисления с длинами оказывались под угрозой.

Интересно, что позже, в рукописи «Выпрямляющий кривое» (в рамках нашей статьи это предельно интригующее название — чуть позже станет понятно почему) некоего Альфонсо, предположительно, крещеного еврея, жившего в Испании между XIII и XV веками, к несоразмерности длин отношение уже гораздо более доброжелательное:

Учебник Атанасян по геометрии

Учебник А.Г. Атанасяна по геометрии – одно из наиболее популярных учебных пособий для обучения геометрии в 7 классе. Этот учебник широко применяется во многих школах России и имеет репутацию надежного и качественного учебного пособия.

Учебник Атанасяна по геометрии в 7 классе охватывает разнообразные темы, включая понятие и свойства отрезка, прямой, угла, треугольника, четырехугольника и круга. Пособие содержит подробные объяснения, иллюстрации и задачи для самостоятельного решения.

Одна из особенностей учебника Атанасяна – его систематическое и логичное изложение материала. Все понятия и свойства отрезка, а также других геометрических фигур, постепенно вводятся и объясняются, что облегчает понимание материала учениками.

Учебник Атанасяна также отличается четкой структурой и логическим построением каждого урока. Каждый урок начинается с определения и основных понятий, затем следуют примеры и объяснения, а также решение задач. В конце урока предлагаются упражнения для самостоятельного закрепления знаний.

Учебник Атанасяна по геометрии является полным и всеобъемлющим пособием, которое позволяет ученику систематически и глубоко изучать геометрию. Он помогает формировать логическое мышление, развивает умение решать задачи и предоставляет необходимые знания для успешной сдачи экзаменов.

В целом, учебник Атанасяна по геометрии в 7 классе является незаменимым помощником для учеников, которые хотят углубить свои знания в геометрии и достичь успеха в этом предмете.

Направленный отрезок

Когда вы задаете направление для сегмента линии, он называется направленным сегментом линии. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуется стрелка (рис. 5).

Напишите начальную, а затем конечную точку направленного отрезка. На рис. 2 верхний направленный сегмент обозначен следующим образом: \( \маленькая \направленная стрелка \) и нижний сегмент выглядит так: \( \маленькая \направленная стрелка \) Отрезок направления называется вектором.

Содержание раздела

• Точка (геометрия)
• Прямая
• Луч (геометрия)
• Угол
• Отрезок
• Серединный перпендикуляр к отрезку
• Ломаная
• Пропорциональные отрезки
• Аксиома параллельных прямых
• Смежные углы. Свойства смежных углов
• Вертикальные углы. Свойства вертикальных углов
• Перпендикулярные прямые
• Перпендикуляр к прямой
• Параллельные прямые. Признаки параллельности прямых
• Теоремы об углах, образованных двумя параллельными прямыми и секущей
• Биссектриса угла. Свойства
• Теорема Пифагора онлайн
• Теорема, обратная теореме Пифагора
• Теорема Фалеса. Доказательство
• Треугольники. Признаки равенства треугольников
• Подобные треугольники. Признаки подобия треугольников
• Биссектриса треугольника онлайн
• Серединные перпендикуляры к сторонам треугольника
• Теорема о биссектрисе треугольника. Доказательство
• Высота треугольника онлайн
• Теорема Стюарта. Доказательство
• Теорема синусов. Доказательство
• Теорема косинусов. Доказательство
• Решение треугольников онлайн
• Прямоугольный треугольник. Онлайн калькулятор
• Равнобедренный треугольник. Онлайн калькулятор
• Сумма углов треугольника
• Внешний угол треугольника
• Виды треугольников
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника
• Средняя линия треугольника
• Теорема Менелая
• Окружность, описанная около треугольника
• Радиус описанной окружности около треугольника онлайн
• Радиус описанной окружности около равнобедренного треугольника онлайн
• Радиус описанной окружности около равностороннего треугольника онлайн
• Радиус описанной окружности около прямоугольного треугольника онлайн
• Окружность, вписанная в треугольник
• Радиус вписанной в треугольник окружности онлайн
• Радиус вписанной окружности в равнобедренный треугольник онлайн
• Радиус вписанной окружности в равносторонний треугольник онлайн
• Радиус вписанной окружности в прямоугольный треугольник онлайн
• Окружность и круг. Онлайн калькулятор
• Взаимное расположение прямой и окружности
• Касательная к окружности
• Центральный угол окружности. Градусная мера дуги окружности
• Вписанный угол окружности
• Квадрат. Онлайн калькулятор
• Прямоугольник. Онлайн калькулятор
• Параллелограмм
• Ромб
• Сторона ромба онлайн
• Высота ромба онлайн
• Площадь ромба онлайн
• Диагонали ромба онлайн
• Трапеция. Определение, виды, свойства
• Четырехугольник
• Четырехугольник, вписанный в окружность
• Окружность, вписанная в четырехугольник
• Многоугольник
• Площадь треугольника онлайн
• Площадь прямоугольного треугольника онлайн
• Площадь равностороннего треугольника онлайн
• Площадь равнобедренного треугольника онлайн
• Площадь квадрата онлайн
• Площадь прямоугольника онлайн

Фракталы

Подробнее об этом виде кривых мы писали тут. Однако в рамках разговора об эволюции представлений о кривых не упомянуть их невозможно. Классическим примером фрактала (фигуры со свойством самоподобия) является кривая Коха.

Свойство самоподобия означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:

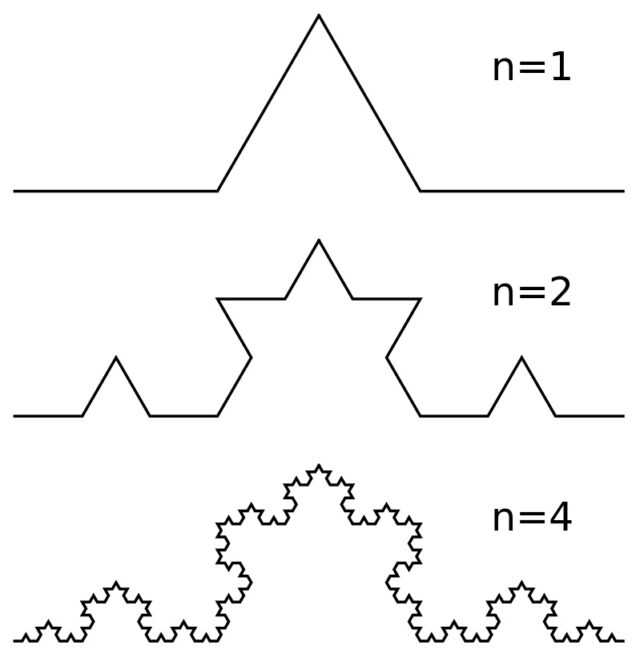
В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.

Наш подход с прямыми отрезками терпит здесь фиаско — вместо приближения к какой-то конечной длине сумма длин отрезков неограниченно растет.

Конечно, кривые, обладающие этим свойством, не исчерпываются самоподобными фигурами. Достаточно найти трещину на стене не самой простой формы: самоподобия в ней мы, как правило, не наблюдаем, и в то же время от одной ее «ветки» отходят новые, иной формы, и т. д.

Свойства отрезка: все, что нужно знать об основных понятиях и определениях

Отрезок в математике — это часть прямой, ограниченная двумя точками. Он имеет много свойств, которые помогают в его изучении и решении задач. Ниже представлены основные понятия и определения, связанные с свойствами отрезка.

1. Длина отрезка

Длина отрезка — это величина, равная расстоянию между его конечными точками. Обозначается символом |AB|, где A и B — конечные точки отрезка AB. Длина отрезка всегда является положительным числом.

2. Середина отрезка

Середина отрезка — это точка, равноудаленная от его конечных точек. Обозначается символом M. Для нахождения середины отрезка AB можно использовать формулу M = (A + B) / 2, где A и B — координаты конечных точек.

3. Частное деление отрезка

Частное деление отрезка — это разбиение отрезка на две части в заданном отношении. Обозначается символом P. Частное деление отрезка AB на отношение k:1 означает, что отрезок AP к отрезку PB имеет длину k:1.

4. Угол наклона отрезка

Угол наклона отрезка — это угол между прямой, на которой лежит отрезок, и положительным направлением оси ОХ. Обозначается символом α и измеряется в градусах. Угол наклона отрезка может быть положительным или отрицательным, в зависимости от направления оси ОХ.

5. Перпендикулярный отрезок

Перпендикулярный отрезок — это отрезок, образованный пересечением двух перпендикулярных прямых. Он обладает свойством, что угол между ним и перпендикулярным отрезком равен 90 градусам.

6. Параллельный отрезок

Параллельный отрезок — это отрезок, лежащий на параллельных прямых. Он имеет свойство, что угол между ним и параллельным отрезком равен 0 градусам.

7. Площадь отрезка

Площадь отрезка — это величина, которая равна произведению длины отрезка на его ширину (перпендикуляр к отрезку). Обозначается символом S. Площадь отрезка всегда является неотрицательной величиной.

Это лишь некоторые из основных понятий и определений, связанных со свойствами отрезка. Знание этих понятий поможет более точно и глубже изучать отрезки и использовать их свойства в математических рассуждениях и решении задач.

Греция: длина без ширины

Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:

Определение 1.1. Точка — это то, часть чего есть ничто.

Определение 1.2. Линия — это длина без ширины.

Определение 1.3. Концы линий — это точки.

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)

Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.

Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):

Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.

В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.

Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.

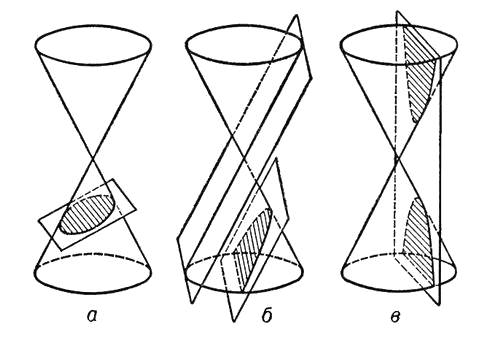
Приведем и несколько других примеров, известных грекам.

Циссоида Диокла:

Конхоида Никомеда:

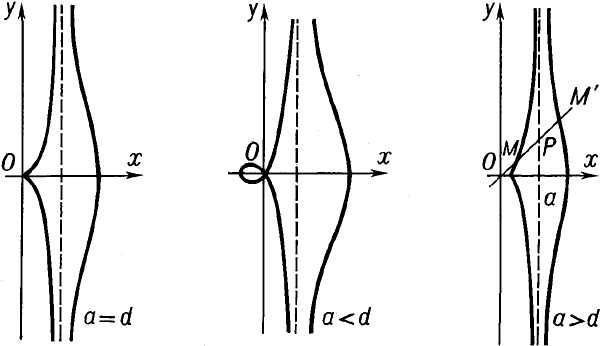
Знаменитая архимедова спираль: