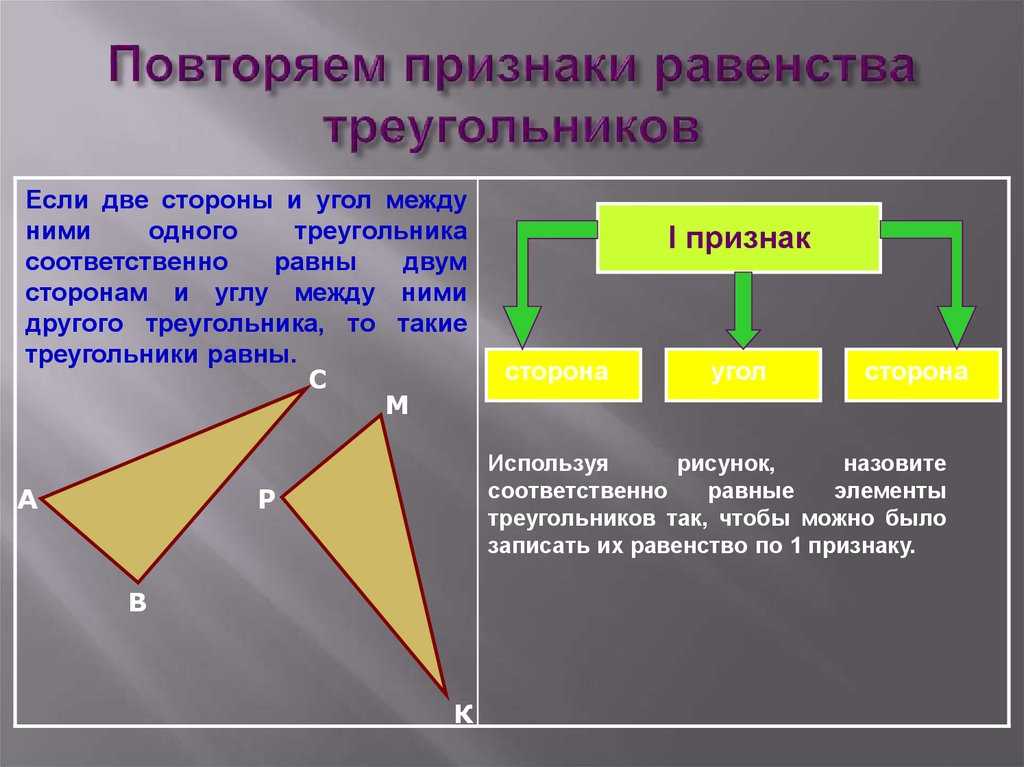
Признаки равенства треугольников - определение и вычисление с примерами решения

Доказательство подобия треугольников

Чуть позже появляется ещё одна важная тема «Подобие треугольников». Само определение «подобие» в геометрии означает схожесть формы при различии размеров. Для примера можно взять два квадрата, первый со стороной 4 см, а второй 10 см. Эти виды четырёхугольников будут похожи и, одновременно, иметь отличие, поскольку второй будет больше, причём каждая сторона увеличена в одинаковое количество раз.

В рассмотрении темы подобия также приводятся 3 признака:

Первый о двух соответственно равных углах двух рассматриваемых треугольных фигур.
Второй об угле и образующих его сторонах ∆ MNK , которые равны соответственным элементам ∆ SDH .
Третий указывает на пропорциональность всех соответственных сторон двух нужных фигур.

Как же доказать, что треугольники подобны? Достаточно воспользоваться одним из выше перечисленных признаков и грамотно описать весь процесс доказательства задания. Тема подобия ∆ MNK и ∆ SDH проще воспринимается школьниками исходя из того, что к моменту её изучения ученики уже свободно пользуются обозначениями элементов в геометрических построениях, не путаются в огромном количестве названий и умеют читать чертежи.

Завершая прохождение обширной темы треугольных геометрических фигур, учащиеся уже в совершенстве должны знать, как доказать равенство ∆ MNK = ∆ SDH по двум сторонам, установить равны два треугольника или нет

Учитывая, что многоугольник, имеющий ровно три угла — это одна из важнейших геометрических фигур, к усвоению материала следует подойти серьёзно, уделяя особое внимание даже мелким фактам теории

Включен угол треугольника (определение и примеры)

, написанный

Malcolm McKinsey

26 января 2023

Проверка по фактам

Paul Mazzola

В комплекте Угол.

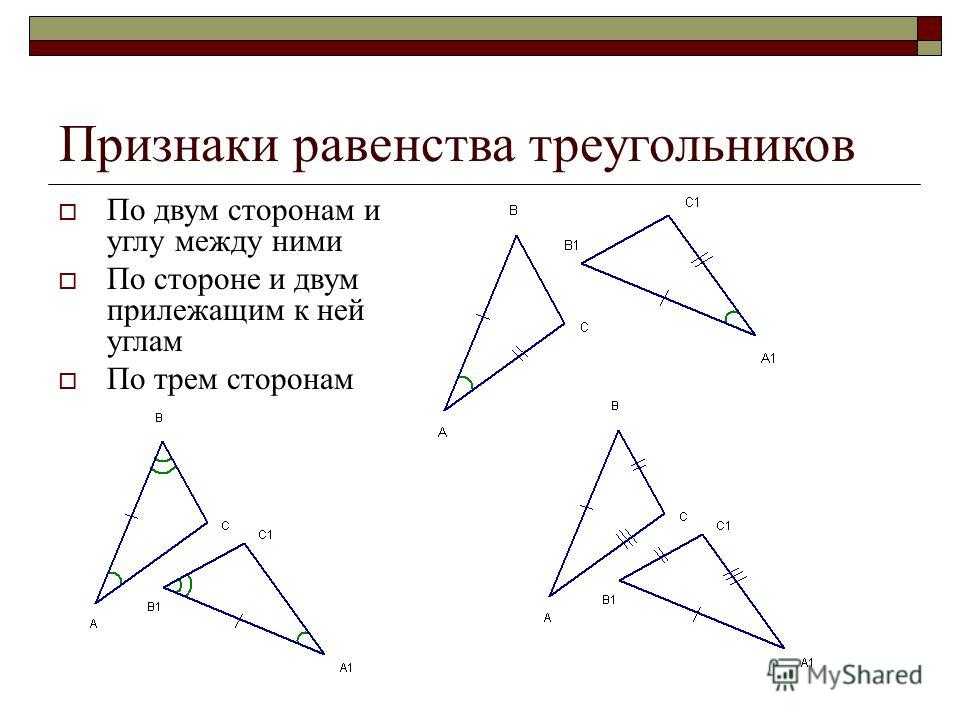
Чтобы найти углы между ними, начните со сторон:

NA and AP include ∠A\angle A∠A between them
AP and PN include ∠P\angle P∠P between them
PN и NA Включите N \ Angle Nomats между ними

.0017

Is ∠E\ угол E∠E включенный угол для сторон JE и TJ ?

№; ∠J\угол J∠J — их внутренний угол. ∠E\угол E∠E – угол между сторонами JE и ET .

Геометрия позволяет начать с простейших измерений земли (« геометрия» означает « земная мера» ) и построена на более сложных понятиях.

Включенные углы в геометрии

Большинство Студенты-математики считают, что геометрию немного легче понять, чем тригонометрию. Итак, давайте сначала рассмотрим вложенные углы в геометрии. В формальных доказательствах каждый раз, когда вы видите угол, зажатый между другими элементами, вы используете включенный угол:

Конгруэнтность

Изобразите два равнобедренных треугольника. Первый равнобедренный треугольник имеет катет 14 дециметров длины и основание 12 дециметров . Прилежащий угол равен 67° . Посмотрите на второй рисунок. Он имеет такие же измерения.

Два равнобедренных треугольника конгруэнтны ?

Благодаря теореме о стороне, углу и стороне, которая утверждает, что два треугольника конгруэнтны, если две их стороны и угол между ними конгруэнтны. Вы математически знаете, что эти два равнобедренных треугольника конгруэнтны.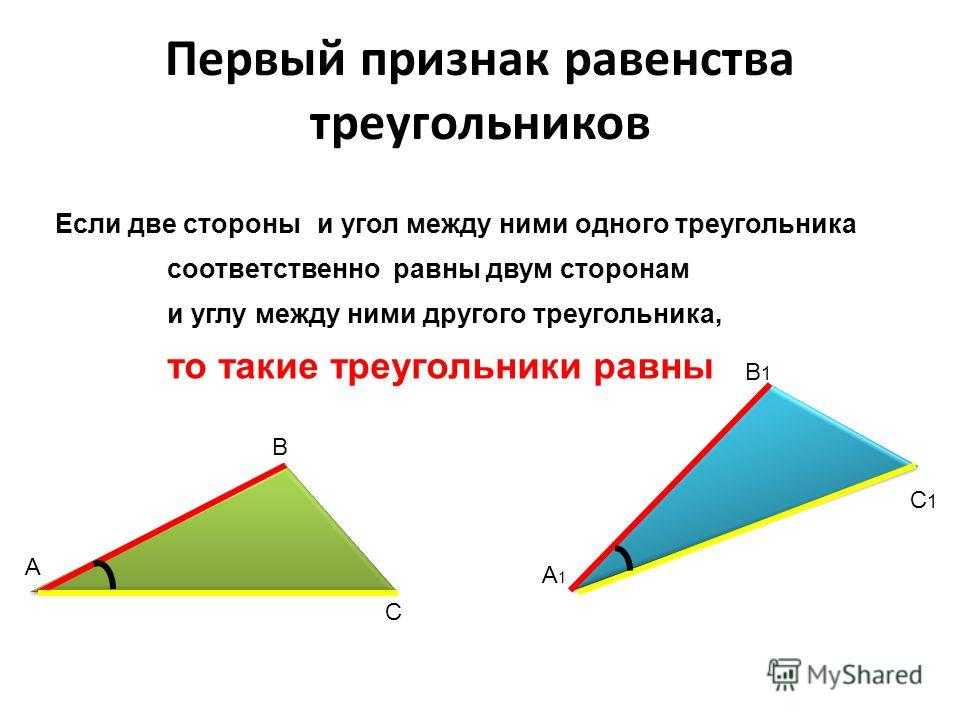

Подобие

Та же концепция применима к подобию треугольников: теорема (или постулат) о подобия стороне и угла говорит нам, что два треугольника подобны, если две соответствующие стороны пропорциональны, а угол между ними конгруэнтен. Вот новый тупоугольный треугольник △CAR\треугольник CAR△CAR, который можно сравнить с △JET\треугольником JET△JET выше.

Notice that side AR = 21 m and RC = 27 m , while our original △JET\triangle JET△JET had ET = 7 m , TJ = 9 м .

Угол между ними, ∠R\угол R∠R в △CAR\треугольнике CAR△CAR и ∠T\угол T∠T в △JET\треугольник JET△JET, оба равны ≈ 108,0° . Эти два треугольника подобны?

У нашего нового △CAR\треугольника CAR△CAR стороны в три раза длиннее, чем у △JET\треугольника JET△JET , но между соответствующими сторонами такой же угол.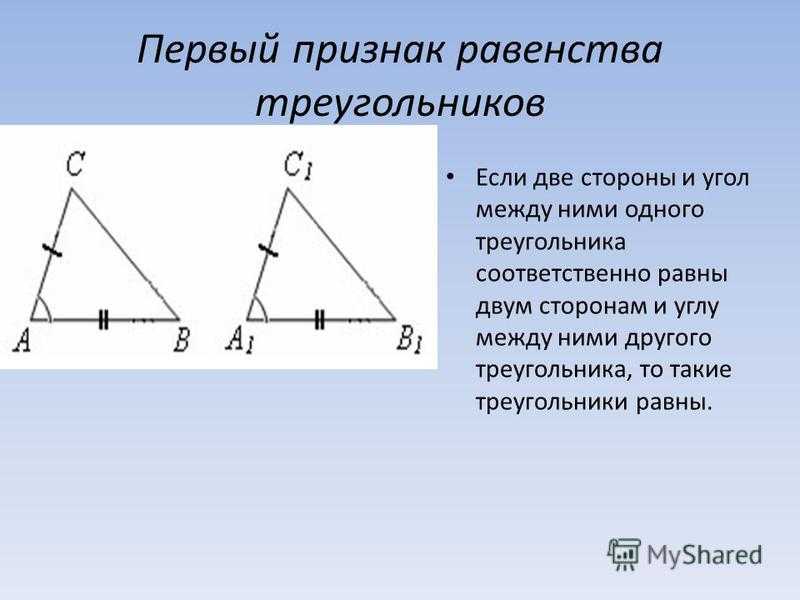

Углы, включенные в тригонометрию

Тригонометрия позволяет находить свойства треугольников, например площадь, используя только отношения между сторонами и углами. В то время как геометрия предлагает формулу для площади, A=12bhA=\frac{1}{2}bhA=21bh, тригонометрия предлагает другую формулу, где A = площадь треугольника, a и b – длины сторон, а C – их угол между ними:

Здесь вы умножаете длины двух сторон на синус прилежащего к ним угла, а затем берете половину этого (поскольку треугольник — это половина прямоугольника).

Предположим, у вас есть государственный парк треугольной формы, известный своими стадами диких зоидов, бродящих по широким открытым пространствам:

.0025 a и сторона YD будет нашей стороной b .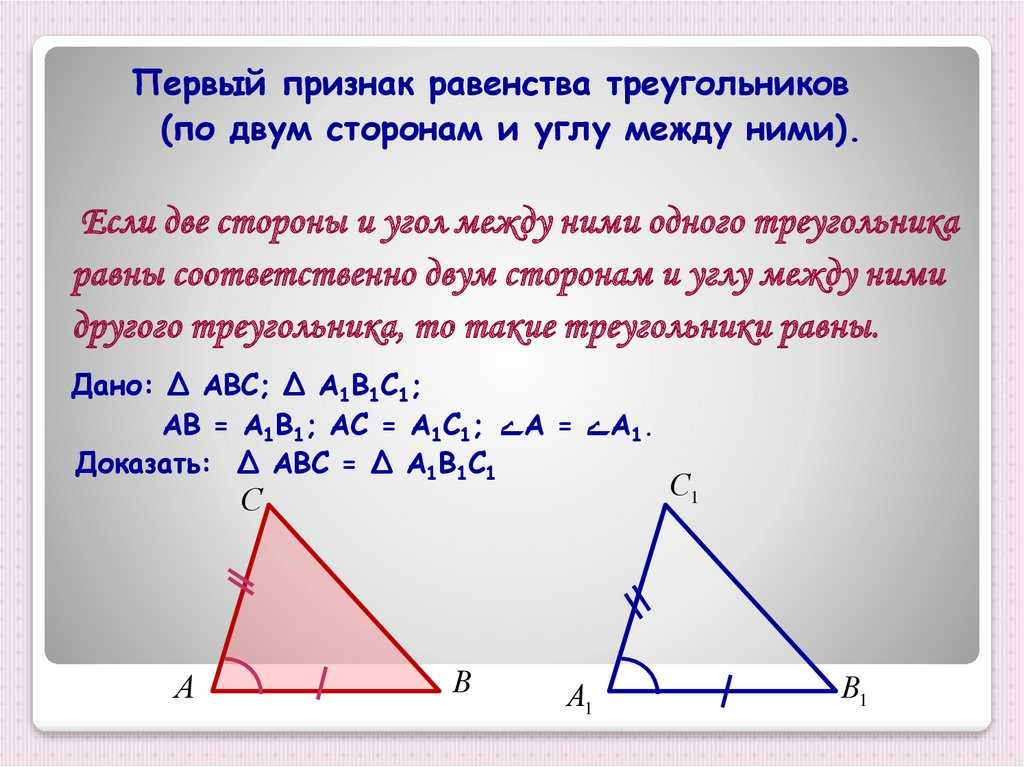 Нам нужно только найти синус ∠Y\угол Y∠Y, 105° , чтобы найти площадь.

Подставьте то, что вы знаете:

Если 181 квадратный километр кажется большим, помните, что мы рисовали государственный парк, полный широких открытых пространств, куда вы можете пойти, чтобы поймать зоида .

После изучения этого урока вы теперь можете определить угол между любыми двумя сторонами любого треугольника, использовать углы между ними в геометрических доказательствах подобия и конгруэнтности и применить формулу тригонометрии для нахождения площади треугольника. треугольник, A=12absin⁡(C)A=\frac{1}{2}ab\sin\left(C\right)A=21absin(C), где a и b — стороны треугольника, а C — угол между ними.

Неравенство треугольника

Следующий факт касается не углов, а сторон треугольника.

Это означает, что:

$ a+b>c$
$ a+c>b$
$ b+c>a$

Ты уже догадался, почему этот факт называется неравенством треугольника?

Ну вот, а где же это неравенство треугольника может оказаться полезным?

А представь, что у тебя есть три друга: Коля, Петя и Сергей.

И вот, Коля говорит: «От моего дома до Петиного $ 100$ м по прямой». А Петя: «От моего дома до дома Сергея $ 200$ метров по прямой». А Сергей: «Вам хорошо, а от моего дома до Колиного аж $ 500$ м по прямой».

Ну, тут уже ты должен сказать: «Стоп, стоп! Кто – то из вас говорит неправду!»

Так не может быть!

Почему?

Да потому что если от Коли до Пети $ 100$ м, а от Пети до Сергея $ 200$ м, то от Коли до Сергея точно должно быть меньше $ 300$ ($ =100+200$) метров – иначе и нарушается то самое неравенство треугольника.

Ну и здравый смысл точно, естественно, нарушается: ведь всякому с детства неизвестно, что путь до прямой ($ КС$) должен быть короче, чем путь с заходом в точку $ П$. ($ К-П-С$).

Так что неравенство треугольника просто отражает этот общеизвестный факт. Ну вот, ты теперь знаешь, как отвечать на такой, скажем, вопрос:

Бывает ли треугольник со сторонами $ 1,3,7$?

Ты должен проверить, правда ли, что любые два числа из этих трёх в сумме больше третьего. Проверяем: $ 1+3<7$, значит, треугольника со сторонами $ 1,3$ и $ 7$ не бывает! А вот со сторонами $ 2,4,5$ – бывает, потому что

Пример задачи

Диагонали AC и BD параллелограмма ABCD пересекаются в точке E. Докажите, что △AED = △BEC.

Решение 1

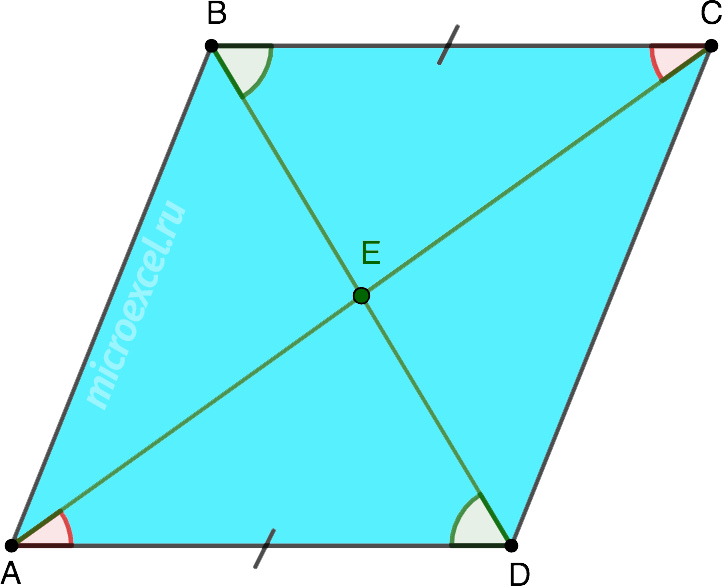
Т. к. это параллелограмм, его противоположные стороны равны, т. е. AD=BC.

Диагональ AC, также, является секущей, которая пересекает две параллельные прямые, на которых лежат стороны AD и BC. Как известно, внутренние накрест лежащие углы попарно равны, следовательно, ∠СAD = ∠ACB. Аналогичным образом, равны углы ∠BDA и ∠DBC.

Значит, рассматриваемые нами треугольники △AED и △BEC равны по второму признаку равенства (по стороне и 2 прилежащим к ней углам).

Примечание: таким же способом можно доказать, что △AEB = △CED.

Решение 2

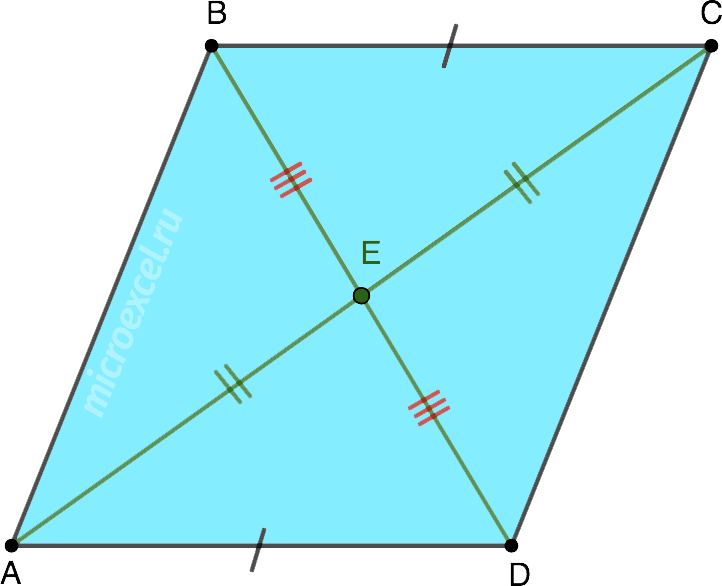
Диагонали параллелограмма в точке пересечения делятся пополам, т. е. AE=EC и BE=ED. Также противоположные стороны параллелограмма равны, т. е. BC=AD.

Таким образом, △AED и △BEC равны согласно третьему признаку равенства (по трем сторонам).

Примечание: Аналогичным образом можно доказать равенство △AEB и △CED.

Решение 3

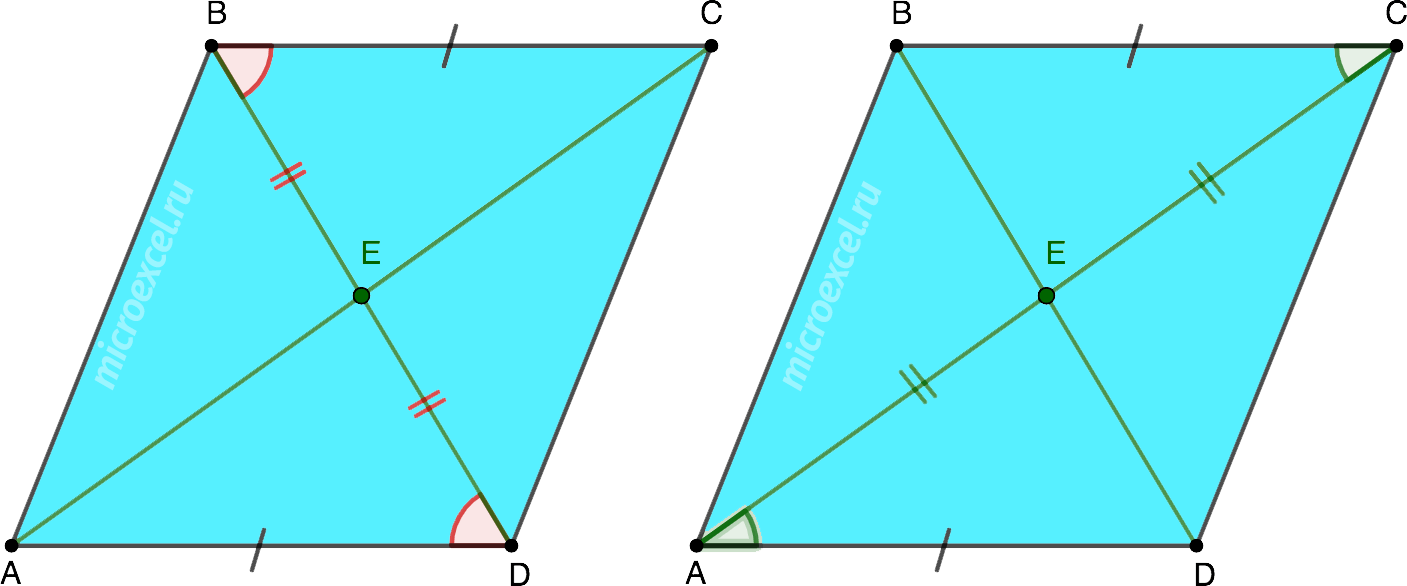
Разбирая решения 1 и 2 мы уже выяснили, что накрест лежащие углы равны, а диагонали параллелограмма в точке пересечения делятся на две одинаковые части.

С учетом этого, доказать равенство треугольников △AED и △BEC (или △AEB и △CED) можно, сославшись на первый признак (по двум сторонам и углу между ними).

Публикации по теме:

Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади трапеции: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра прямоугольника: формула и задачи Нахождение периметра ромба: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема куба: формула и задачи Нахождение объема шара: формула и задачи Нахождение объема пирамиды: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение площади поверхности куба: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса шара: формула и примеры Нахождение радиуса круга: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади правильной призмы: формула и задачи Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема Менелая: формулировка и пример с решением Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Теорема Фалеса: формулировка и пример решения задачи Геометрическая фигура: треугольник Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равностороннего треугольника: теория и пример задачи Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника

Задачи и решения

Упражнение 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E лежит на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (рис.9).

Докажите, что треугольники AC=AD, AE=AB, ∠CAD являются общими для треугольников CAE и DAB. Тогда по первому критерию подобия треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно, ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, CBD=180°−∠DBA. Соответствует CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательств.

Упражнение 2. По рисунку 10 докажите, что OP=OT, ∠P=∠T

Доказательство.OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальны (следовательно, равны), поэтому, повторяя тест подобия треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательств.

MathScene — Векторы — Урок 4

2008 Расмус Эф и Джанн Сак

Урок 4

Скалярное произведение и перпендикулярные векторы

Как
можно ли найти угол между двумя векторами? Правило косинусов выглядит многообещающе, поскольку мы
С его помощью можно найти угол между двумя сторонами треугольника.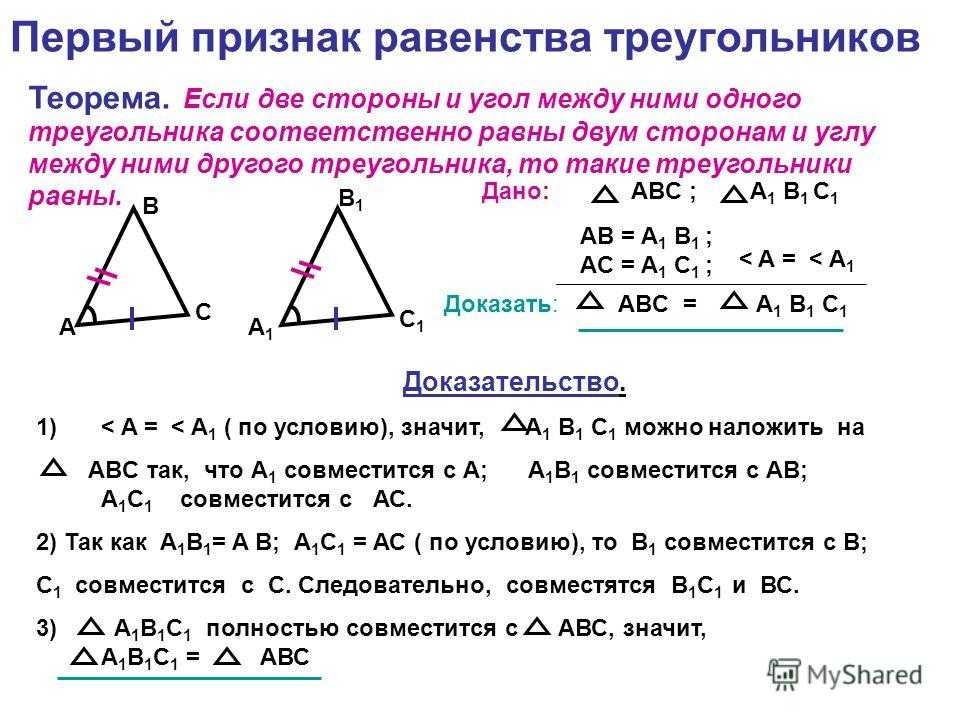

В этом примере легко найти векторы, считая квадраты, но мы
будет использовать общую форму для любого вектора:

Правило косинуса выглядит следующим образом:

в 2 = а 2 + б 2 − 2∙b∙a∙cos C

стороны треугольника имеют длины ||,
||
и |
−
|.
Если обозначить треугольник так, что сторона a = ||,
б = ||
и с = |
−
|
и обозначим угол C как v, мы получим:

|
— | 2 = || 2 + || 2 — 2∙||∙
||∙cos
v

Теперь мы можем использовать формулу расстояния, чтобы найти длину векторов. Мы можем
опустите квадратный корень, поскольку мы возводим в квадрат длины.

(х _а — х _б ) 2 + (y _a − y _b ) 2 = x _a 2 + у _а 2 + х _б 2 + у _б 2 −
2∙||∙
||∙cos
v

Если мы упростим левую часть, умножив скобки, получится:

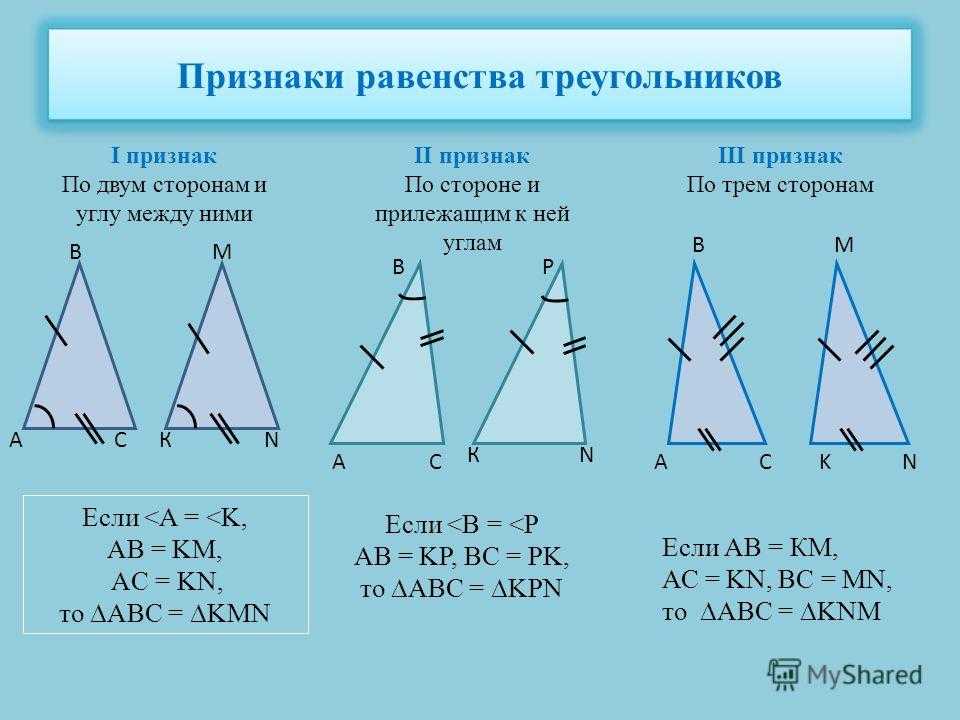
х _а 2 − 2x _a x _b + x _b 2 + у _а 2 —
2г _а г _б + г _б 2

Подставляя это в формулу, мы видим, что все члены в квадрате сокращаются, и мы
остаются с уравнением

−
2x _a x _b − 2y _a y _b = — 2∙||∙
||∙cos
v

Разделив на −2, мы получим следующую важную формулу:

х _а х _б + у _а у _б =
||∙
||∙cos
v

Каждая часть этого уравнения называется скалярным произведением двух векторов. В другом
слов:

скалярное произведение и знак равно
x _a x _b + y _a y _b и скалярное произведение и знак равно
||||кос
v

Символ скалярного произведения — это точка, похожая на символ, иногда используемый для
умножение.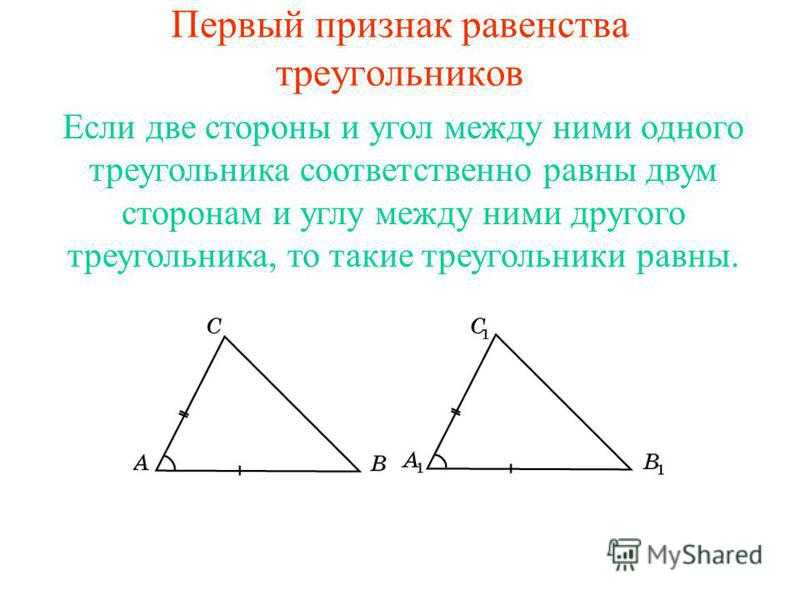

∙
= х _а х _б + y _a y _b и
∙
= ||∙
||∙cos
v

Пример 1

Напишите скалярное произведение векторов и в
следующую схему двумя разными способами.

Мы
может считывать координаты векторов прямо с диаграммы. Мы также можем
см. длину вектора
но
нам нужно вычислить длину вектора
.

Использование координат для нахождения скалярного произведения:

∙
= 3∙4 + 3∙0 = 12

Координаты x перемножаются, y
координаты перемножаются, а затем два результата складываются
все вместе .

Используя другое определение скалярного произведения с длинами векторов и косинусом, мы
получить:

||
=

||
= 4

Теперь мы ответим на поставленный нами вопрос и посмотрим, как мы можем найти
угол между двумя векторами.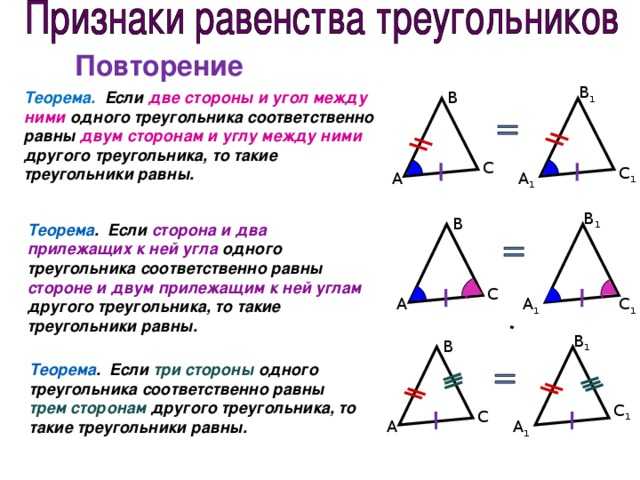

Для этого мы используем обе формы скалярного произведения.

х _а х _б + у _а у _б = ||∙
||∙cos
v

Разделив на
||||
получаем следующую формулу:

Если мы используем формулу расстояния, чтобы найти длины, это будет:

Пример
2

Найдите углы между векторами

≈ 0,8575

в
≈ потому что −1 0,8575
≈ 31

Пример
3

Найдите вектор такой же длины, как и
перпендикулярно к
.

Мы называем этот вектор и
напишите формулу скалярного произведения
и .

х _а х _б + у _а у _б = ||∙
||∙cos
90

Но cos 90 = 0, поэтому мы получаем следующий результат:

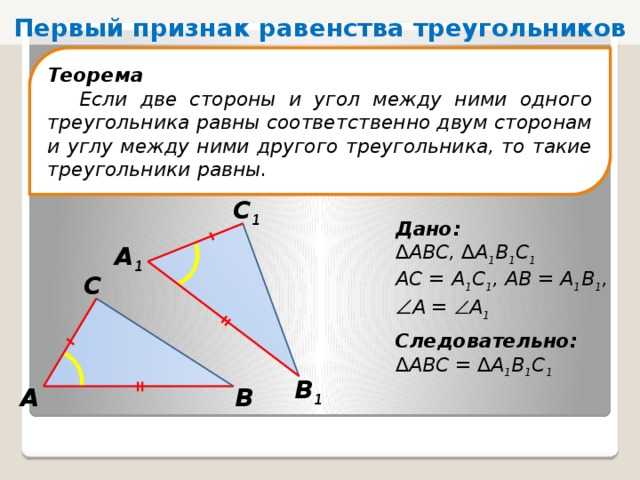
Икс
+ 2г = 0

Мы также знаем, что || 2 = х 2 + у 2 = 5.

Решая эти два уравнения вместе, мы получаем , x + 2y = 0 и x 2 + у 2 = 5.

х = -2у и х 2 = 5 — у 2

х 2 = 4г 2 = 5 — г 2

5 лет 2 = 5

у 2 = 1

у =
1

Если
y = 1, то x = −2, а если y = −1, то x = 2.

Это означает, что у нас есть две возможности

На диаграмме мы видим эти два результата.

Обобщая приведенные выше результаты, мы видим, что мы можем найти два вектора, которые
перпендикулярны друг другу и имеют одинаковую длину путем переключения вокруг x и
координаты y и изменение знака
по одной из координат.

Вектор перпендикулярно и

Это связано с тем, что угол между перпендикулярными векторами равен 90, а cos
90 = 0

Если
вектор
является
перпендикулярно вектору
затем
их скалярное произведение равно нулю.

х _а х _б + у _а у _б = 0

Верно и обратное этому правилу.

Если
скалярное произведение двух векторов равно нулю, то они перпендикулярны
друг с другом.

Пример
4

Треугольник ABC имеет вершины A = (3, 4), B = (17, 12) и C = (5, 16). Найди
углы треугольника.

Сначала мы находим векторы, представляющие стороны.

Нам больше не нужно выполнять какую-либо работу, так как векторы
и находятся
явно перпендикулярны и равны по длине. Следовательно, треугольник является прямым
равнобедренный треугольник с углами A = 90, B = 45 и C = 45.

Пример
5

Решение задач

Пример 1:

Дано:АС = ВС, АD = BD, ∠CAD =

Найти:∠CBD.

Решение: Выполним пояснительный рисунок:

Рис. 3. Чертеж к примеру 1

Значит, треугольники АСD и ВСD равны по третьему признаку равенства треугольников, то есть по трем сторонам. Из равенства треугольников следует равенство соответствующих углов. ∠СВD = ∠САD =

Ответ:

Пример 2:

Дано: АО = ОВ, СО = ОD.

Доказать:треугольник ADC = треугольникуBCD.

Доказательство. Выполним пояснительный рисунок:

Рис. 4. Чертеж к примеру 2

1. треугольник АОС = треугольнику BOD. Эти треугольники равны по первому признаку равенства треугольников (СО = OD – по условию, АО = ОВ – по условию, ∠АОС = ∠DOB – как вертикальные). Отсюда следует, что АС = BD. Обозначим их за .

2. треугольник ВОС = треугольнику АOD. Эти треугольники равны по первому признаку равенства треугольников (СО = OD – по условию, АО = ОВ – по условию, ∠СОВ = ∠DOА – как вертикальные). Отсюда следует, что ВС = АD. Обозначим их за .

3. .

Отсюда следует, что треугольники ADC и BCD равны по третьему признаку равенства треугольников, что и требовалось доказать.

Ответ: Доказано.

Пример 3:

Дано: АВ = CD, AC = BD, ∠BAC =

Найти:∠CDB.

Решение: Выполним пояснительный рисунок:

Рис. 5. Чертеж к примеру 3

1) треугольник ВАС = треугольнику CDB по третьему признаку равенства треугольников (ВС – общая сторона, АВ = CD – по условию, АС = BD – по условию).

2) ∠CDB = ∠ВАС =. Это следует из равенства треугольников. Оба угла лежат против общей стороны ВС.

Ответ:

Пример 4:

Дано: АВ = ВС = CD = DA.

Доказать:∠1 = ∠2 = ∠3 = ∠4.

Доказательство: Выполним пояснительный рисунок:

Рис. 6. Чертеж к примеру 4

1. треугольник АСВ = треугольнику АСD по третьему признаку равенства треугольников (АС – общая сторона, другие стороны равны по условию). Из равенства треугольников имеем равенство соответствующих углов. ∠1 = ∠2, ∠3 = ∠4.

2. Треугольник АВС – равнобедренный, а значит,∠1 = ∠3. Треугольник АСD – также равнобедренный, ∠2 = ∠4.

3. ∠1 = ∠2 = ∠3 = ∠4, что и требовалось доказать.

Ответ: Доказано.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/zadachi-na-tretiy-priznak-ravenstva-treugolnikov

https://www.youtube.com/watch?v=ei5hiZvwrbk

https://www.youtube.com/watch?v=rJVHGfMqGkk

Задачи на третий признак равенства треугольников

http://school-assistant.ru/?predmet=geometr&theme=priznaki_ravenstva_treugolnikov

http://oftob.ru/categories/2-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0-6-%D0%B2%D0%B8%D0%BB%D0%B5%D0%BD%D0%BA%D0%B8%D0%BD-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F

Второй признак равенства треугольников

Теорема:

Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла.

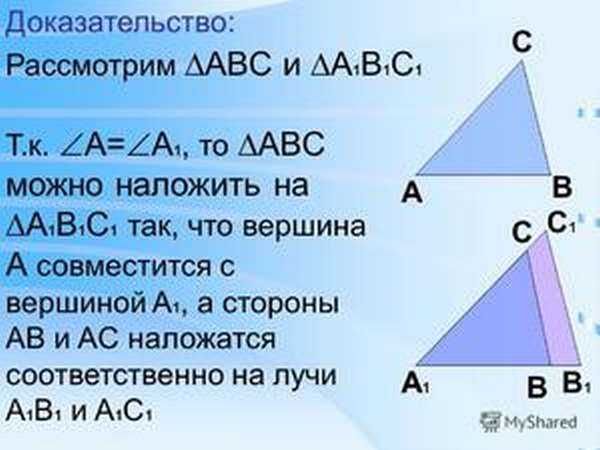
Доказательство:

Рассмотрим два треугольника ABC и A₁B₁C₁, у которых:

AC = A₁C₁, ∠A = ∠A₁ и ∠C = ∠C₁.

Требуется доказать, что

ABC = A₁B₁C₁.

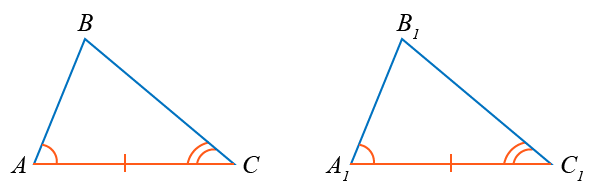
Если наложить A₁B₁C₁ на ABC так, чтобы точка A₁ совместилась с точкой A и сторона A₁C₁ совместилась со стороной AC, то точка C₁ совпадёт с точкой C, так как A₁C₁ = AC. Сторона A₁B₁ совпадёт со стороной AB, так как ∠A = ∠A₁. Сторона C₁B₁ совпадёт со стороной CB, так как ∠C = ∠C₁. Вершина B₁ совпадёт с вершиной B, так как B и B₁ будут служить точками пересечения одних и тех же отрезков. Таким образом, треугольники совместятся. Теорема доказана.

Третий признак равенства треугольников

Доказательство. Даны два треугольника $\bigtriangleup{ABC}$ и $\bigtriangleup{A_{1}B_{1}C_1}$, в которых $AB=A_{1}B_1,~BC=B_{1}C_1$ и $CA=C_{1}A_1$. Наложим треугольники друг на друга так, чтобы вершина $C_1$ располагалась в одной полуплоскости с вершиной $C$. Поскольку $AB=A_{1}B_1,$ точка $A$ совпадет с точкой $A_1,$ точка $B$ совпадет с точкой $B_1$.

Воспользуемся методом доказательства от противного и предположим, что при наложении точка $C_1$ не лежит ни на луче $BC$, ни на луче $AC$. Тогда между вершинами $C$ и $C_1$ имеется расстояние $CC_1$. Обозначим точку $D$ как середину этого отрезка.

Рассмотрим треугольники $\bigtriangleup{AC_{1}C}$ и $\bigtriangleup{BC_{1}C}$.

Они являются равнобедренными, с общим основанием $CC_1$. В них $AD$ и $BD$ — медианы, поскольку $D$ мы обозначали как середину $CC_1$.

По теореме о медиане равнобедренного треугольника, медианы $AD$ и $BD$ также будут являться высотами соответствующих треугольников. Согласно теореме о единственности перпендикуляра, к точке прямой можно провести только один перпендикуляр. У нас — два перпендикуляра $AD$ и $BD$, к одной точке $D$.

Мы пришли к противоречию. Значит, точка $C_1$ располагается либо на луче $AC$, либо на луче $BC$. Если $C_1\in{AC},$ тогда $C_1$ совпадает с точкой $C$, поскольку $CA=C_{1}A_1$. Точно так же приходим к выводу о совпадении точек $C$ и $C_1,$ если $C_1\in{BC}$. Все три точки совпадают. Треугольники равны.

Теорема доказана.

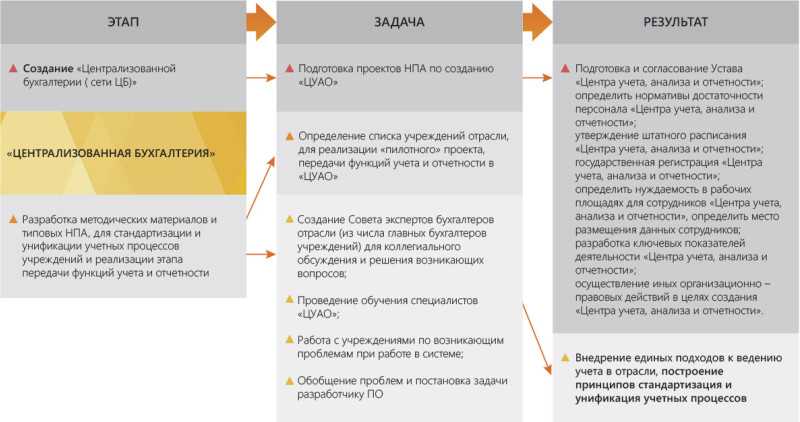
{"questions":[{"content":"`image-1` Перед вами — различные пары треугольников. Определите на чертеже, где какой признак равенства. `matcher-5`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/02/test-2-1.svg"},"matcher-5":{"type":"matcher","labels":,"items":}}}]}

Сумма углов треугольника. Внутренние и внешние углы

Внутренние углы треугольника

Единственное, что тебя может смущать в нашей формулировке – это слово «внутренних».

Зачем оно тут? А вот именно затем, чтобы подчеркнуть, что речь идёт об углах, которые внутри треугольника.

А что, разве бывают ещё какие-то углы снаружи? Вот представь себе, бывают.

У треугольника ещё бывают внешние углы.

И самое главное следствие из того факта, что сумма внутренних углов треугольника равна $ \displaystyle 180{}^\circ $, касается как раз внешнего треугольника.

Внешние углы треугольника

Так что давай выясним, что же такое этот внешний угол треугольника.

Смотри на картинку: берём треугольник и одну сторону (скажем $ \displaystyle AC$) продолжаем.

Видишь, получился новый угол, $ \displaystyle \angle BCE$?

Этот угол образован одной стороной ($ \displaystyle BC$) треугольника и продолжением другой стороны ($ \displaystyle AC$).

Вот он и называется внешним углом треугольника $ \displaystyle ABC$ при вершине $ \displaystyle C$.

Конечно, мы бы могли оставить сторону $ \displaystyle AC$, а продолжить сторону $ \displaystyle BC$. Вот так:

Тогда $ \displaystyle \angle ACK$ тоже будет внешним углом при вершине $ \displaystyle C$, да и к тому же он будет равен углу $ \displaystyle BCE$.

Смотри:

Углы $ \displaystyle BCE$ и $ \displaystyle ACK$ – равны как вертикальные, и оба они имеют право называться внешним углом при вершине $ \displaystyle C$.

А вот про угол $ \displaystyle ECK$ такого сказать ни в коем случае нельзя!

Он образован пересечением двух продолжений сторон!

Угол $ \displaystyle ECK$ вообще равен внутреннему $ \displaystyle \angle C$ треугольника $ \displaystyle ABC$.

Так что же мы должны знать про внешний угол?

Смотри, на нашем рисунке это означает, что $ \angle 4=\angle 1+\angle 2$.

Как же это связано с суммой углов треугольника?

Давай разберёмся. Сумма внутренних углов равна $ \displaystyle 180{}^\circ \Rightarrow $

$ \angle 1+\angle 2+\angle 3=180{}^\circ $,

но $ \angle 4+\angle 3=180{}^\circ $ – потому, что $ \angle 3$ и $ \angle 4$ – смежные.

Ну вот и получается: $ \angle 4=\angle 1+\angle 2$.

Видишь как просто?! Но очень важно. Так что запоминай:

Немного об импликациях

Несмотря на то, что прямое и обратное следствия для равнобедренных треугольников оказались истинными, мы не можем, к примеру, сказать то же про вертикальные углы. Действительно, если углы равны… то они вертикальны? Далеко не факт. Иными словами, истинность импликации не гарантирует истинность обратной импликации.

В быту же законы логики соблюдаются редко: мы все время перемешиваем меж собой заключения и условия и, что страшнее, превращаем корреляции в импликации. Например, всем давно известная корреляция между геймингом и детской жестокостью. Нужно понимать, что корреляция — это не более чем статистическая взаимосвязь случайных величин.

Скажем, автомобилист Гриша на третьем перекрестке по дороге домой всегда попадает на зеленый свет светофора. Имеем ли мы право перейти от случайной корреляции к фактическому следствию «если $A$, то $B$»? То есть сказать: «Если Гриша едет домой, то светофор всегда будет зеленым»?

К сожалению, люди размышляют именно так. Корреляция «часто жестокие дети играют в компьютерные игры» превращается в импликацию «если дети играют в игры, то они становятся жестокими».

Или еще хуже, в обратную импликацию: «если ребенок жестокий, то он играет в компьютерные игры».

Первое дает возможность родителям безапелляционно контролировать детей. Второе — снимать какую-либо ответственность за жестокое поведение ребенка с окружения. Импликация — мощное оружие. Особенно когда она используется вне законов науки логики. Так что в следующий раз, если услышите нечто подобное, можете смело заявить о некорректном переходе от корреляции к импликации.