Квадрат. онлайн калькулятор

Свойства квадрата

1. Длины сторон квадрата равны.

AB=BC=CD=DA

2. Все углы квадрата прямые.

\angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^{\circ}

3. Противолежащие стороны квадрата параллельны друг другу.

AB \parallel CD, BC \parallel AD

4. Сумма всех углов квадрата равна 360 градусов.

\angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ}

5. Величина угла между диагональю и стороной равна 45 градусов.

\angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^{\circ}

Доказательство

Квадрат является ромбом \Rightarrow
AC
— биссектриса угла A
, и он равняется 45^{\circ}
. Тогда AC
делит \angle A
, и \angle C
на 2
угла по 45^{\circ}
.

6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.

AO = BO = CO = DO

\angle AOB = \angle BOC = \angle COD = \angle AOD = 90^{\circ}

AC = BD

Доказательство

Так как квадрат это прямоугольник \Rightarrow
диагонали равны; так как — ромб \Rightarrow
диагонали перпендикулярны. А так как — параллелограмм, \Rightarrow
диагонали разделены точкой пересечения пополам.

7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника.

\triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD

8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника.

\triangle AOB = \triangle BOC = \triangle COD = \triangle AOD

9. Если сторона квадрата равна a, то, диагональ будет равна a \sqrt{2}
.

— (лат. quadratum, от quadrare сделать четырехугольным). 1) прямоугольный, равносторонний четырехугольник. 2) такое число, которое, будучи умножено само на себя, дает данное число. 3) единица для измерения плоскостей; напр.: квадратн. фут, дюйм и… … Словарь иностранных слов русского языка

В квадрате. Жарг. мол. Пренебр. О крайне тупом, безнадёжно глупом человеке. /i> Квадрат глупый, несообразительный чаловек. Никитина 1996, 82. Квадрат твою гипотенузу! Жарг. шк. Бран. Выражение досады, раздражения, негодования. ВМН 2003, 62.… … Большой словарь русских поговорок

КВАДРАТ, в биологии квадратная рама, используемая для разметки участка поверхности с целью изучения растений, находящихся на нем. Квадратом называют также и сам этот участок почвы. Как правило, такой квадрат равен 0,5 или 1 м2. Пользуясь этим… … Научно-технический энциклопедический словарь

КВАДРАТ, квадрата, муж. (лат. quadratus четырехугольный). 1. Равносторонний прямоугольник (мат.). 2. Форма такого прямоугольника у какого нибудь предмета (книжн.). Ярко освещенный квадрат окна. 3. Четырехугольный гартовый брусок мера для… … Толковый словарь Ушакова

Муж. равносторонний и прямоугольный четыреугольник; народ называет его круглым четыреугольником или клеткою. Разбить площадь на квадраты, на участки этого вида. | Квадрат числа, произведение его от умножения самого на себя. Узор квадратцами или… … Толковый словарь Даля

В полиграфии, 1) единица длины, применяемая для измерения шрифтов, формата набора. 1 квадрат = 48 пунктам (ок. 18,05 мм).2) Разновидность пробельного материала для заполнения крупных промежутков в строках … Большой Энциклопедический словарь

Параллелограмм, клетка, материал, прямоугольник, степень, квадратик Словарь русских синонимов. квадрат сущ., кол во синонимов: 9 гиперкуб (12) … Словарь синонимов

квадрат
— КВАДРАТ, а, м. Тюрьма; камера. квадрат топтать находиться в тюрьме, камере. Из уг … Словарь русского арго

квадрат
— (Quad) 1. Одна из основных единиц типометрической системы Дидо, равная 4 цицеро, или 48 пунктам. 1 квадрат равен 18,048 мм. 2. Пробельный материал, используемый при изготовлении наборных печатных форм способа высокой печати. Квадраты различают по … Шрифтовая терминология

«Квадрат»
— «Квадрат», клуб любителей джазовой музыки (джаз клуб). Создан в 1964 при ДК имени Ленсовета (с 1965 размещался в ДК имени С. М. Кирова, с 1986 во Дворце молодёжи). Объединяет музыкантов и любителей классического джаза. «Квадрат» продолжил… … Энциклопедический справочник «Санкт-Петербург»

— (от латинского quadratus четырехугольный), 1) равносторонний прямоугольник. 2) Вторая степень a2 числа a (название связано с тем, что именно так выражается площадь квадрата со стороной a) … Современная энциклопедия

Книги

• Квадрат. Из истории российского джаза , . В книге собраны избранные материалы по истории российского джаза, публиковавшиеся в 60-80-е годы прошлого века на страницах легендарного неофициального самиздатского машинописного журнала…
• Квадрат , Вилли Карлссон. Книгу видного деятеля Коммунистической партии Дании можно назвать подлинной летописью рабочего движения в стране в бурную эпоху с начала кризиса 30-X годов до оккупации Дании нацистами.…

Когда у них одинаковые длины диагоналей, сторон и равные углы.

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• Квадрат: периметр = 4 * сторона.
• Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
• Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
• Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• Параллелограмм: площадь = основание * высота
• Квадрат: площадь = сторона 1 * сторона 2
• Треугольник: площадь = ½ * основание * высота
• Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• интерактивные задания больше похожи на игру;
• их можно отрабатывать многократно и они не будут повторяться;
• платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
• достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Квадрат в математике

Квадрат — это одна из важных фигур в математике. Он представляет собой геометрическую фигуру, которая имеет четыре равных стороны и четыре прямых угла. Центр квадрата находится в точке пересечения его диагоналей. Каждая сторона квадрата состоит из клеток, которые могут быть пронумерованы для удобства.

Когда говорят о квадрате в математике, это может относиться не только к физическому представлению фигуры, но и к ее абстрактному значению. Например, на графике, квадрат может представлять определенный сегмент или область. Квадратный график создается с помощью значений x и y, которые представляют длину каждой стороны квадрата.

Квадрат часто используется в математических выражениях, формулах и уравнениях. Он может быть использован для определения площади и периметра других фигур, а также для решения различных задач и проблем. Квадрат также является основой для изучения других геометрических фигур, таких как прямоугольник, ромб и параллелограмм.

В математике, квадрат также может быть разделен на четверти, которые являются равными прямоугольными фигурами. Каждая четверть квадрата имеет свои характеристики, такие как углы, стороны и площадь. Квадрат можно представить в виде матрицы или таблицы, где каждая ячейка соответствует клетке квадрата.

Алгебраическое определение квадрата

Чтобы описать алгебраическое определение квадрата, нужно обратить внимание на его основные характеристики. Квадрат представляет собой специальный вид прямоугольника, у которого все стороны равны между собой

Таким образом, он является квадратным и имеет клетчатую структуру.

В случае квадрата, каждая его сторона и угол имеют одинаковую длину. Это условие делает его геометрическим объектом, отличным от прямоугольников с произвольными сторонами. Каждая сторона квадрата может быть равной, например, а.

Квадрат также имеет свои четверти, представляющие собой четыре части, на которые он может быть разделен. Центр квадрата находится в точке пересечения его диагоналей и является центром симметрии фигуры.

Когда говорят о квадрате, часто упоминают его площадь и периметр. Площадь квадрата можно вычислить по формуле S = a * a, где а — длина стороны квадрата. Периметр определяется как сумма всех сторон квадрата: P = 4 * a.

Квадратные уравнения и формулы

Квадратные уравнения могут быть записаны в виде ax2 + bx + c = 0, где a, b и c — коэффициенты, а x — переменная. Центральной частью этого уравнения является квадратный член ax2, который представляет собой квадрат переменной x.

Решение квадратного уравнения может быть найдено с использованием формулы дискриминанта. Дискриминант D = b2 — 4ac позволяет определить, сколько корней имеет уравнение. Если D > 0, то у уравнения два действительных корня, если D = 0, то уравнение имеет один действительный корень, а если D

График квадратного уравнения представляет собой параболу, которая может быть открытой вверх или вниз, в зависимости от значения коэффициента a. Если a > 0, то парабола открыта вверх, а если a

Изучение квадратных уравнений полезно при решении различных задач о нахождении максимумов или минимумов, определении значений функций и нахождении координат вершин параболы. Квадратные уравнения также часто используются в физике для моделирования движения и прогнозирования.

В случае, когда нужно найти координаты вершин параболы, используют формулы: x = -b/2a и y = f(x).

Основные понятия

Основные геометрические фигуры на плоскости состоят из точек, линий, лучей, отрезков и вершин. У каждого предмета есть свои особенности, свойства и предназначение. Самый минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет измерительных мер: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Чтобы правильно решить задачу, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Объемные геометрические фигуры:

• шар;
• конус;
• параллелепипед;
• цилиндр;
• пирамида;
• сфера.

В начальной школе дети узнают названия геометрических фигур и учатся различать плоские от объемных. Сейчас мы рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

На уроках математики в Skysmart дети решают увлекательные задачки в интерактивном формате, рисуют пальцами на онлайн-доске и помогают героям красочных комиксов. Приходите вместе с ребенком на бесплатный вводный урок: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Квадрат — определение и свойства

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.

2. Диагонали квадрата равны и пересекаются под прямым углом.

Периметр квадрата P в 4 раза больше его стороны и равен:

Площадь квадрата равна квадрату его стороны: .

Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть .

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

Тогда , что и требовалось доказать.

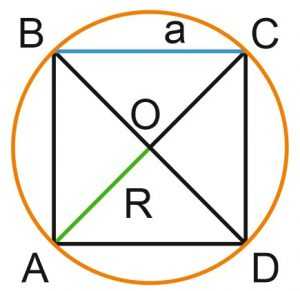
Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна .

Мы знаем, что . Тогда .

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

Тогда по формуле площади квадрата:

Второй способ решения:

Воспользуемся формулой для площади ромба:

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Радиус описанной окружности равен половине диагонали квадрата, поэтому

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата: .

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Задача 8. Найдите площадь квадрата, в который вписан круг площадью .

Площадь круга откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .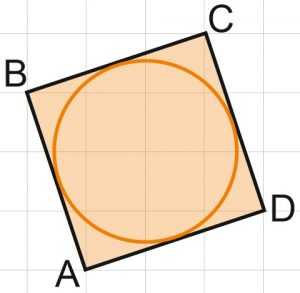

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .

Определение и характеристики квадрата в математике

В математике квадрат – это специальный вид прямоугольника, у которого все стороны имеют одинаковую длину. Формально квадрат можно определить как выпуклый многоугольник с четырьмя равными сторонами и углами, равными 90 градусам. В геометрии квадрат часто обозначается символом «□».

Основными характеристиками квадрата являются:

1. Длина стороны: В квадрате все стороны равны друг другу. Обозначение длины стороны обычно осуществляется буквой «а».
2. Площадь: Площадь квадрата вычисляется по формуле: S = a^2, где «S» — площадь, «a» — длина стороны квадрата.
3. Периметр: Периметр квадрата вычисляется по формуле: P = 4a, где «P» — периметр, «a» — длина стороны квадрата.
4. Диагональ: Диагональ квадрата – это отрезок, соединяющий противоположные вершины квадрата. В квадратах диагонали равны друг другу и определяются с помощью формулы: d = a√2, где «d» — диагональ, «a» — длина стороны квадрата.

Важно отметить, что квадрат является частным случаем прямоугольника, ромба и параллелограмма. Также квадрат обладает рядом свойств, которые можно использовать при решении задач:

• Все углы квадрата прямые. В силу своей формы, квадрат имеет углы в 90 градусов.
• Диагонали квадрата равны. Противоположные диагонали в квадрате равны друг другу.
• Сумма углов в квадрате равна 360 градусов. Так как квадрат имеет 4 прямых угла по 90 градусов, их сумма равна 360 градусов.
• Сумма длин двух противоположных сторон квадрата равна нулю. Сумма длин двух противоположных сторон всегда равна нулю.

Знание определения и характеристик квадрата позволяет эффективно решать задачи связанные с геометрией, а также применять его свойства для вычислений и доказательств.

Квадрат как геометрическая фигура

Квадрат – это геометрическая фигура, которая имеет четыре равные стороны и четыре прямых угла. В геометрии квадрат обозначается символом «а». Квадрат относится к квадратным фигурам, так как у него все стороны и углы равны.

Квадрат можно представить как специальный случай прямоугольника, у которого все стороны равны друг другу. В отличие от прямоугольника, стороны квадрата всегда перпендикулярны друг другу и образуют прямые углы.

Квадрат используется в различных областях. Например, в математике квадраты могут использоваться для построения графиков функций. Квадратные координатные системы используются для представления данных и визуализации результатов исследований или статистических данных.

Квадрат также может быть использован как базовая единица измерения. Он может быть разделен на одинаковые части, такие как клетки, чтобы упростить задачу измерения и оценки площади.

Квадрат имеет также несколько характеристических точек и линий. Центр квадрата – это точка, которая находится в середине фигуры и имеет равное расстояние до всех сторон. Квадрат также имеет четыре вершины – угловые точки, образованные пересечением сторон.

Говоря о квадрате, нельзя не упомянуть о четвертях и квадрантах. Четверти – это равные части квадрата, которые могут быть получены путем проведения горизонтальной и вертикальной линий, проходящих через его центр. Квадрантов в квадрате также четыре – они образованы пересечением сторон и полу-диагоналей квадрата.

Определение и свойства квадрата

Квадрат – это геометрическая фигура, которая имеет особые свойства и характеристики. Главное отличие квадрата от других фигур в том, что все его стороны равны друг другу, и углы прямые. Поэтому он называется квадратным.

Квадрат можно увидеть в различных случаях в повседневной жизни. Например, в сетке на листе бумаги или на шахматной доске. В алгебре квадрат часто используется в качестве базовой единицы в графике координатной плоскости.

Квадрат состоит из четырех сторон и четырех углов. Все его углы равны 90 градусам, что делает его особенно устойчивым и симметричным. Квадрат также имеет две диагонали, которые равны друг другу и делят его на четыре равные части, которые называются четвертями.

Свойство квадрата заключается в том, что его стороны и диагонали перпендикулярны друг другу. Это означает, что каждая сторона квадрата образует прямой угол со своей соседней стороной и с диагональю. Также каждая диагональ квадрата разделяет его на два прямоугольных треугольника.

Квадрат можно использовать для создания графических элементов и отображения информации. Например, в таблице с данными или для создания иллюстраций и диаграмм. Кроме того, квадрат может использоваться в математических и логических задачах, таких как расчет площади или определение периметра.

Примеры использования квадрата в геометрии

Квадрат является одной из основных геометрических фигур, которая широко используется в различных областях математики и физики. Одним из основных применений квадрата является построение графиков. Квадратная сетка, состоящая из множества квадратных клеток, часто используется для отображения отношений и зависимостей между различными переменными.

Квадрат также активно используется в геометрических вычислениях, связанных с нахождением площадей и периметров фигур. Например, для нахождения площади прямоугольника можно разбить его на сетку квадратных клеток и посчитать количество клеток внутри него.

Еще одним примером использования квадрата в геометрии является его применение в определении различных четвертей плоскости. Центральный квадрат называется центром плоскости, а остальные квадраты разделяют плоскость на четыре равные части, называемые четвертями. Это позволяет легко определить положение точки на плоскости и решать задачи, связанные с координатными плоскостями.

Таким образом, квадрат в геометрии играет важную роль и используется в различных случаях – от построения графиков до определения координат на плоскости. Он является одной из основных геометрических фигур, строго определенной своими сторонами и углами.