Какие фигуры называются окружностью

Главные свойства круга в математике

Определение: круг — это фигура, которая состоит из всех точек на плоскости, расположенных на одинаковом расстоянии от одной фиксированной точки, называемой центром. Это расстояние называется радиусом круга.
Формула для вычисления площади круга: S = πr², где S — площадь круга, r — радиус круга, π (пи) — математическая константа, приближенно равная 3,14159.
Формула для вычисления длины окружности: C = 2πr, где C — длина окружности, r — радиус круга.
Свойства круга:
1. Круг является выпуклым множеством, то есть любые две точки внутри круга можно соединить отрезком, который целиком будет лежать внутри круга.
2. Любая точка на окружности круга находится на равном расстоянии от его центра.
3. Диаметр круга — это отрезок, соединяющий две точки на окружности, проходящий через центр круга. Диаметр всегда равен двум радиусам.
4. Каждый радиус круга проходит через его центр.
5. Любая хорда круга — это отрезок, соединяющий две точки на окружности. Хорда всегда меньше или равна диаметру.
Связь между площадью круга и его радиусом: площадь круга пропорциональна квадрату его радиуса. Если увеличить радиус в 2 раза, то площадь увеличится в 4 раза. Если радиус уменьшить в 2 раза, то площадь уменьшится в 4 раза.

Круг — одна из наиболее изученных фигур в математике. Его свойства и формулы активно применяются в различных областях, таких как геометрия, физика, инженерия и другие.

Окружность и круг: основные различия

В геометрии окружность и круг смыслово связаны, но имеют некоторые отличия. Окружность — это геометрическая фигура, представляющая собой линию, состоящую из всех точек, равноудаленных от центра. Круг же — это теоретическая плоская фигура, ограниченная окружностью.

Главным отличием между окружностью и кругом является то, что окружность не имеет площади, в то время как круг — это круглая фигура с определенной площадью. Круг может быть задан с помощью радиуса и центра, который является точкой внутри круга.

Другое различие между окружностью и кругом заключается в их диаметрах. Диаметр — это отрезок, соединяющий две точки на окружности и проходящий через центр круга. В окружности диаметром считается любой отрезок, проходящий через центр, в то время как в круге диаметр — это двойной радиус.

Таким образом, главная разница между окружностью и кругом заключается в том, что окружность является линией, состоящей из точек, равноудаленных от центра, в то время как круг — это ограниченная этой окружностью плоская фигура с определенной площадью. Кроме того, окружность не имеет площади, в отличие от круга.

Определение и форма

Окружность и круг — две понятия из области геометрии, которые отличаются друг от друга. Окружность — это геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от центра. Центр окружности — это точка, от которой все точки окружности расположены на одинаковом расстоянии, называемом радиусом.

Теория окружностей в геометрии изучает их свойства и особенности. Окружность является формой, которая не имеет начала и конца, она представляет собой замкнутую линию, состоящую из бесконечного числа точек.

Круг — это закрашенная фигура, которая образуется при закрашивании внутренней части окружности. Круг представляет собой плоскую геометрическую фигуру, ограниченную окружностью. Диаметр круга — это отрезок, соединяющий две точки на окружности круга и проходящий через его центр. Диаметр является максимальной длиной от точки к точке на окружности.

В качестве иллюстрации можно представить таблицу с описанием различий между окружностью и кругом:

Окружность	Круг
Геометрическая фигура	Закрашенная фигура
Бесконечная линия	Ограниченная плоская фигура
Состоит из множества точек на одинаковом расстоянии от центра	Состоит из закрашенной области внутри окружности
Центр и радиус определяют окружность	Центр и радиус определяют круг, а также диаметр

Что такое окружность?

Окружность – это геометрическая фигура, которая представляет собой замкнутую линию на плоскости. Она состоит из всех точек, расположенных на одинаковом расстоянии от определенной точки, которую называют центром окружности.

Один из основных параметров окружности – это радиус, который определяет расстояние от центра до любой точки на окружности. Также можно выразить радиус через диаметр окружности. Диаметр – это отрезок, проходящий через центр окружности и соединяющий две противоположные точки на окружности.

Окружность можно охарактеризовать свойствами ее периметра и площади. Периметр окружности вычисляется по формуле 2πr, где r – радиус окружности. Площадь окружности вычисляется по формуле πr².

Чтобы иллюстрировать свойства окружности и ее параметры, можно использовать таблицу или графические примеры. Например, в таблице можно привести значения радиуса, диаметра, периметра и площади окружности для различных значений.

Что такое круг?

Круг — это геометрическая фигура, которая образуется на плоскости при вращении точки вокруг определенной оси, которая называется центром. Линия, которую описывает точка при вращении, называется окружностью. Окружность состоит из всех точек, которые находятся на одинаковом расстоянии от центра.

Одной из основных характеристик круга является его радиус. Радиус — это расстояние от центра круга до любой его точки. Другая основная характеристика круга — диаметр. Диаметр — это отрезок, который соединяет две противоположные точки на окружности и проходит через центр.

Также важным понятием в теории круга является площадь. Площадь круга вычисляется по формуле S = π * r^2, где π — приближенное значение математической константы, равное примерно 3.14, а r — радиус круга.

Круг можно представить с помощью таблицы, где будут указаны его основные характеристики: радиус, диаметр, площадь. Используя эту таблицу, можно легко вычислить значение радиуса или площади круга, если известны другие характеристики.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение.Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Формула.Площадь внешней поверхности сегмента сферы с высотой h
через радиус сферы R:

S = 2π
Rh

Мы даем здесь очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 412) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не плоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, например, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере).

Тогда, обозначая через площадь этого участка — основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):

Если теперь всю поверхность шара разложить на очень большое число N таких малых областей , тем самым объем шара на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой

где последняя сумма равна полной поверхности шара:

Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу

Последний результат формулируется так:

Площадь поверхности шара равна учетверенной площади его большого круга.

Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. сферическую поверхность, или «шапочки»; см. рис. 409). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:

откуда находим для площади шапочки формулу

Шаровым поясом (см. рис. 408) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек:

где — высота слоя. Итак, площадь поверхности шарового пояса для данного шара зависит только от высоты соответствующего слоя, но не от его положения на шаре.

Задача. Боковая поверхность конуса, описанного вокруг шара, имеет площадь, равную полуторной площади поверхности шара. Найти высоту конуса, если радиус шара равен .

Решение. Введем для удобства угол а между высотой и образующей конуса (рис. 413). Найдем для высоты, радиуса основания и образующей конуса выражения

Определение шара

Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее R R
R

— радиус этого шара.

Как найти площадь сферы

Запомните!

Формула площади сферы:
S = 4π
R 2

Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа .
Зная определение степени,
можно записать формулу площади сферы следующим образом. S = 4π
R 2 =
4π
R · R;

Закрепим полученные знания и решим задачу на площадь сферы.

Зубарева 6 класс. Номер 692(а)

Условие задачи:

Вычислите площадь сферы, если её радиус равен
1 =
3 ·
=
=
/ (4 · 3)
= ) =
= ) =
= =
=

88

= 1
R 3 = 1
R = 1 м

Важно!

Уважаемые родители!

При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.

Сфера и шар – это аналог круга и окружности в трехмерном пространстве. Стоит поговорить о каждой из этих фигур, выделить сходства и различия, а так же формулы, свойственные этим фигурам.

Большая часть геометрических построений производится в плоскости, но в старших классах начинают изучать трехмерные фигуры. Двухмерное пространство имеет только две характеристики: длину и ширину. В трехмерных областях добавляется высота. В математике 6 класса изучаются отдельные 3д фигуры.

На плоскости фигуру характеризовала площадь и периметр. В трехмерных объектах к ним прибавляется объем.

Рис. 1. Трехмерное пространство.

Кроме того, имеется ряд специфических свойств 3д фигур. Их может пересекать прямая и плоскость, могут имеется секущие плоскости, которые принимают формы других фигур.

Применение 3д фигур для составления задач значительно усложняет их, но в то же время делает куда более интересными. Приведем определения шара и сферы, после чего попробуем выделить различия этих фигур.

Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

длина двух соприкасающихся в одной вершине сторон — a и b;
градус угла, который образуют эти стороны.

Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

https://youtube.com/watch?v=aXyKgX6RAqw

Площади усеченных частей круга

А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:

Хорда — отрезок, соединяющий любые две точки окружности.

Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.

Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:

где S — площадь сектора, r — радиус круга.

Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.

Площадь сегмента можно найти по формулам:

где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.

Часто задаваемые вопросы о площади круга?

И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Кто впервые научился вычислять площадь круга?

Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.

Углы в окружности

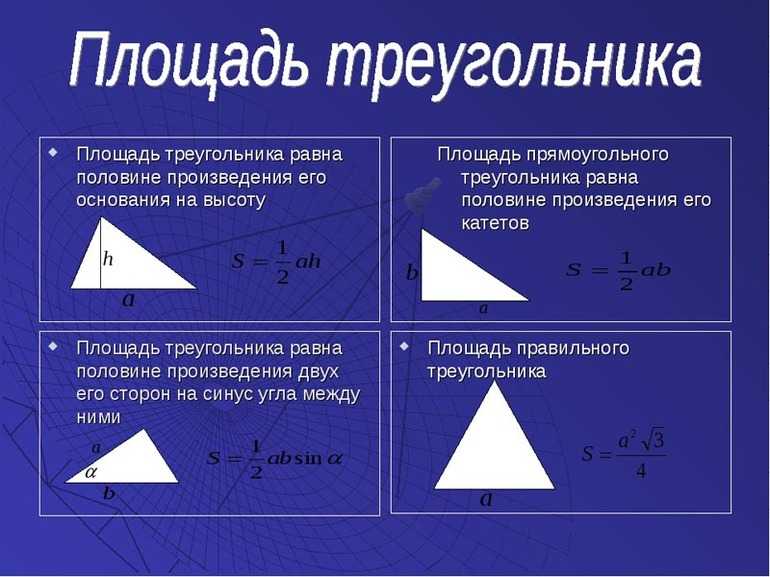
Центральный угол – это угол, вершина которого лежит в центре окружности. В этом случае угол опирается на дугу окружности.

На рисунке угол АОВ будет центральным.

Центральный угловой объект:

Центральный угол равен дуге, на которую он опирается.

Например, дуга АВ равна 36(окружность), тогда и угол АОВ равен 36(окружность).

Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.

На рисунке угол ACB вписанный.

Свойства вписанного угла в окружность:

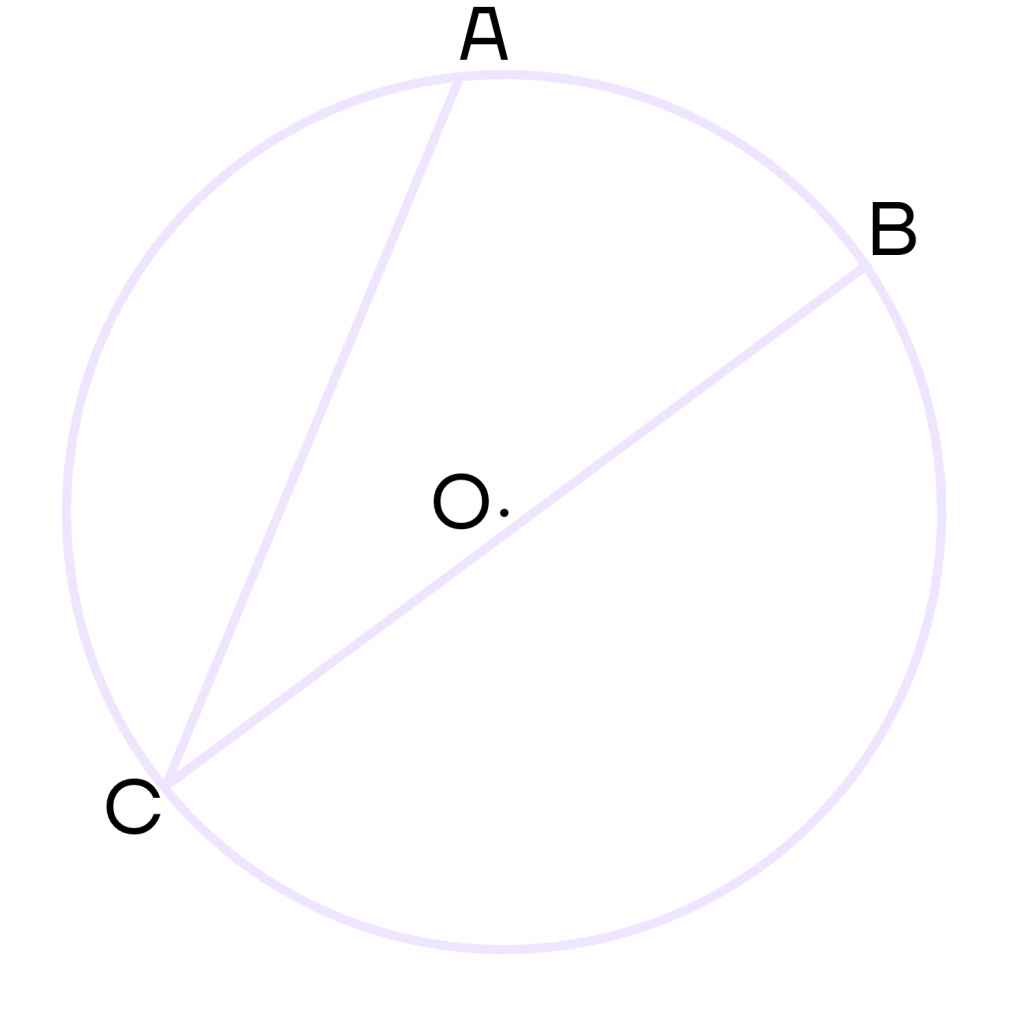
Вписанный угол равен половине дуги, на которую он опирается.

Например, дуга АВ равна 50(окружность), тогда угол АСВ равен 25(окружность).

Вписанные углы, опирающиеся на одну дугу, равны.

Пусть углы DIA, AEB и AKB покоятся на душе AB. Тогда эти углы будут равны между собой.

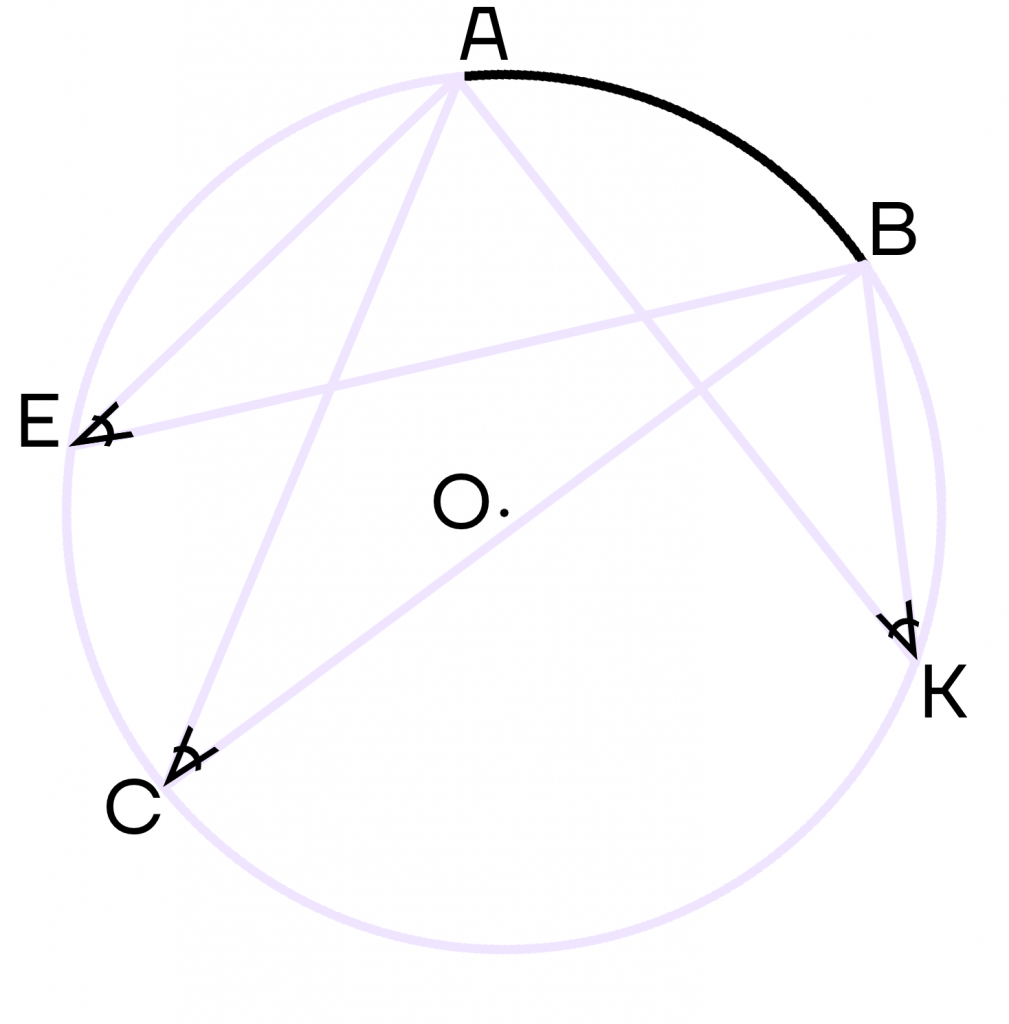
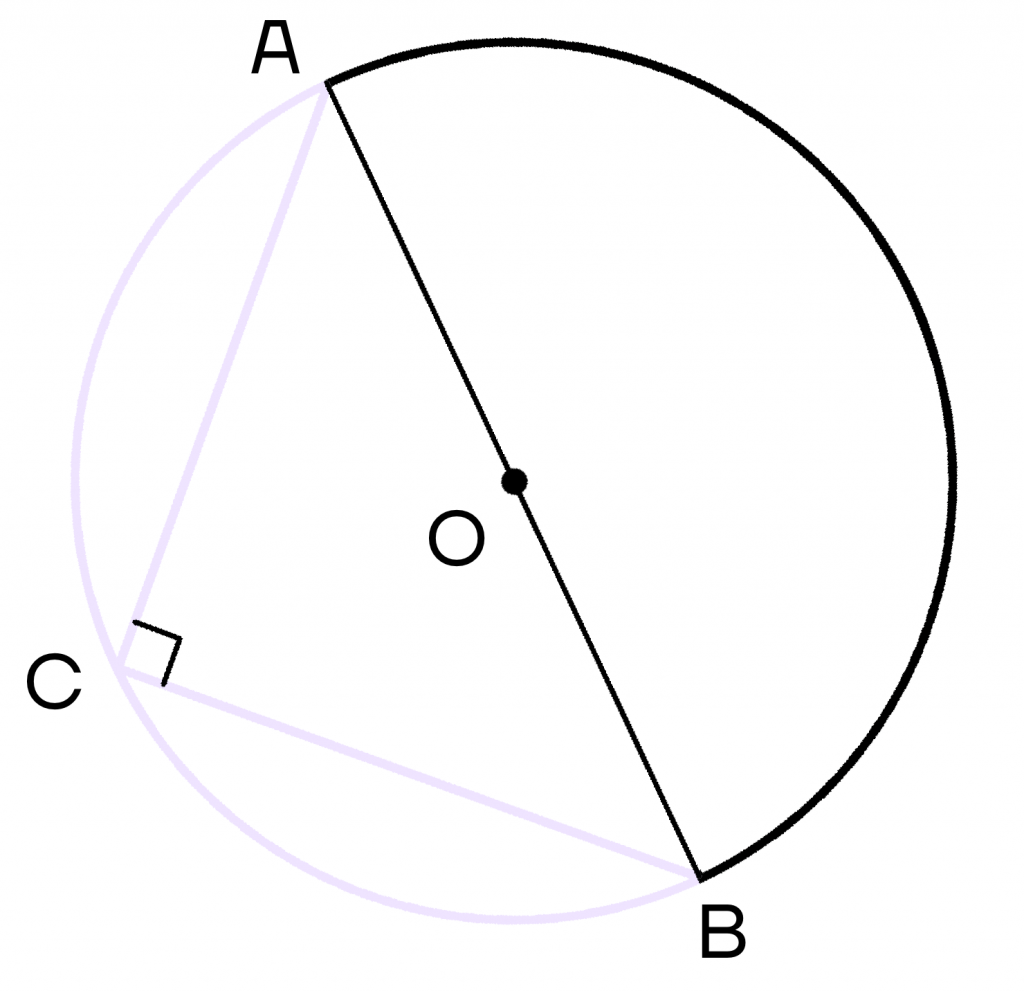
Вписанный угол, основанный на диаметре, равен 90(окружность).

Помните, что диаметр делит окружность на две полуокружности, размер которых равен 180(окружность). Тогда вписанный угол будет 180(окружность) : 2 = 90(окружность).

Также важно отметить, что вписанный угол равен половине центрального угла. При этом эти углы обязательно должны опираться на дугу

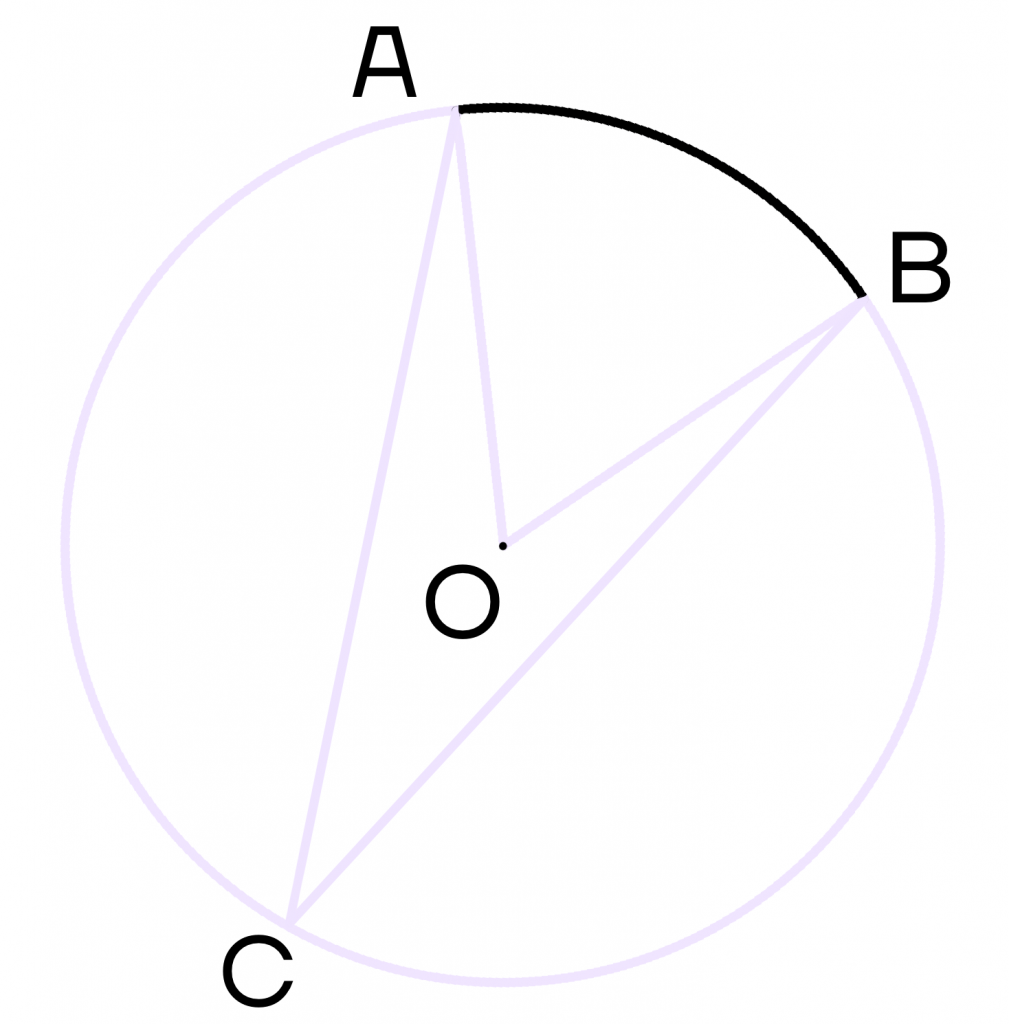
Это легко доказать, если вспомнить, что:

центральный угол равен мере дуги, на которую он опирается,
вписанный угол равен половине градусной меры дуги, на которую он опирается.

Следовательно, (∠ACB = frac{1}{2}∠AOB).

Касательная плоскость к сфере

Плос-ть, имеющая со сферой строго одну общую точку, именуется касательной плоскостью к сфере.

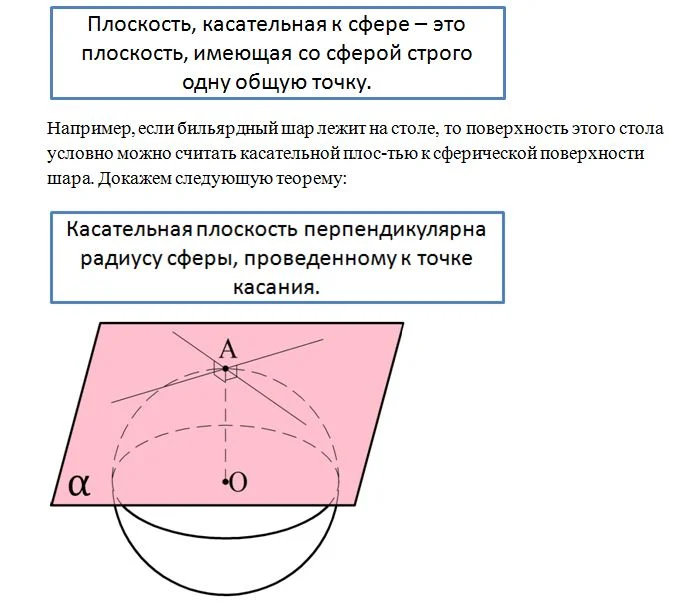
Действительно, если плос-ть касается окруж-ти, то точка касания А должна располагаться на расстоянии R от центра сферы О, где R– радиус сферы. Все остальные точки касательной плос-ти находятся вне пределов сферы, то есть должны находиться от О на расстоянии, превышающем R. Это значит, что отрезок ОА должен быть кратчайшим отрезком, соединяющим О и касательную плос-ть. Но мы знаем, что кратчайший отрезок между плос-тью и точкой – это как раз перпендикуляр, опущенный из точки на плос-ть.

Справедливо и обратное утверждение:

Доказательство. Если радиус ОА – перпендикуляр к плос-ти α, то он является кратчайшим расстоянием между плос-тью и центром О. Тогда все остальные точки плос-ти располагаются на большем расстоянии от О, чем точка А. Это значит, что они не располагаются на сфере. Значит, у сферы и плос-ти α одна общая точка А, а потому α по определению – касательная плос-ть.

По аналогии с касательной плос-тью существует понятие касательной прямой к сфере.

Касательная к сфере обладает почти теми же свойствами, что и касательная к окруж-ти.

Доказательство. Пусть m– касательная прямая к сфере с центром О. обозначим точку касания как А. Далее через прямую m и центр О проведем плос-ть α. Нам надо показать, что ОА⊥m:

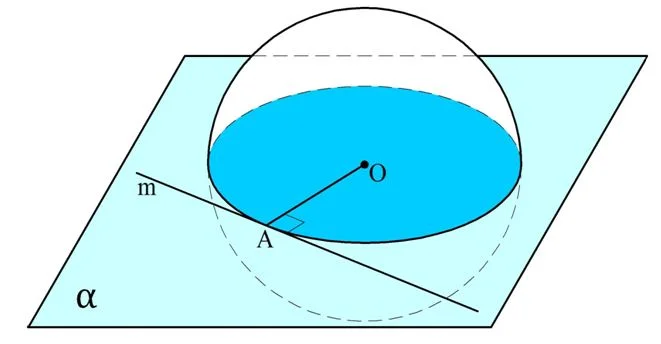
Плос-ть α будет диаметральной плос-тью. Сечение будет иметь форму окруж-ти с центром О и радиусом ОА. Прямая m будет касательной к этой окруж-ти, ведь она имеет с ней общую точку А, а второй общей точки m и окруж-ть иметь не могут, ведь такая бы точка была бы также общей для m и сферы, а m по определению имеет лишь одну общую точку со сферой. Напомним, что касательная к окруж-ти перпендикулярна радиусу, то есть m⊥ОА, ч. т. д.

Будет верным и обратное утверждение:

Для доказательства используем ту же картинку. Известно, что m⊥ОА, надо показать, что m– касательная к сфере. Проведем через пересекающиеся прямые m и ОА плос-ть α. Она снова окажется диаметральной плоскостью, и снова сечением будут окруж-ть с радиусом ОА. По признаку касательной, который мы изучали в планиметрии, m– касательная к этой окруж-ти, ведь m⊥ОА. То есть в плос-ти α есть лишь одна общая точка m и сферы. В других плос-тях у них не может быть общих точек, так как m полностью принадлежит α. В итоге у m и сферы только одна общая точка, а потому m– касательная к сфере, ч. т. д.

Рассмотрим ещё одно утверждение:

Сначала разберемся с понятием отрезков касательных. Пусть из точки А, лежащей вне сферы, к ней проведены две касательные, а точки касания обозначены буквами В и С. Тогда АВ и АС как раз и будут отрезками касательных:

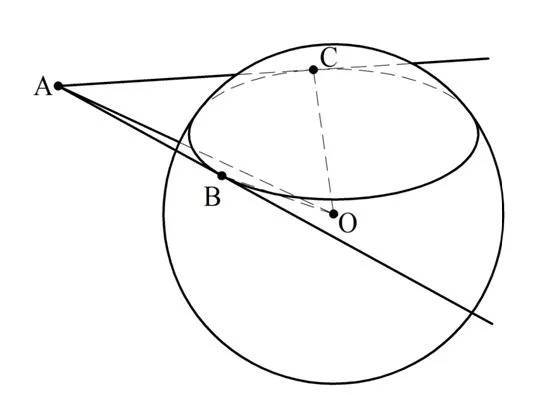
Докажем, что эти отрезки одинаковы. Для этого к точкам касания проведем радиусы ОВ и ОС. Теперь сравним ∆АВО и ∆АСО. Они прямоугольные, ведь ОВ⊥АВ по свойству касательной, и ОС⊥АС. Гипотенуза АО у этих треугольников общая, а катеты ОВ и ОС – это одинаковые радиусы. Получается, что ∆АВО и ∆АСО равны, а потому отрезки АВ и АС одинаковы.

Задание. Дан шар радиусом 10 см, к которому проведена касательная плос-ть α. Через точку касания проведена секущая плос-ть β, образующая с α угол в 30°. Вычислите площадь сечения шара плос-тью β.

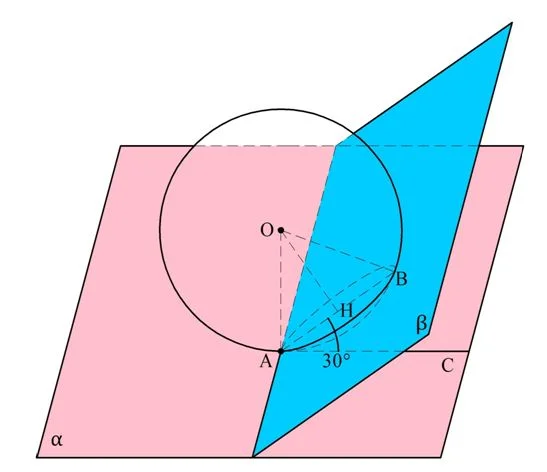
Решение. Обозначим точку касания как А. Опустим из центра сферы о перпендикуляр ОН на плос-ть β. Тогда отрезок АН будет радиусом сечения. Так как угол между плос-тями α и β составляет 30° (на рисунке он показан как ∠НАС), то

Ответ: 25π см2.

Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.

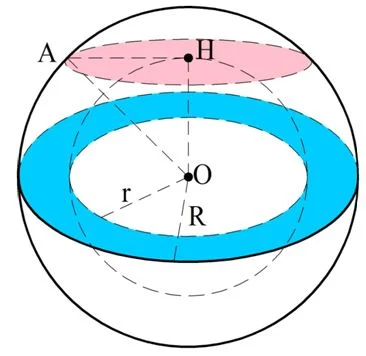
Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:

Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?

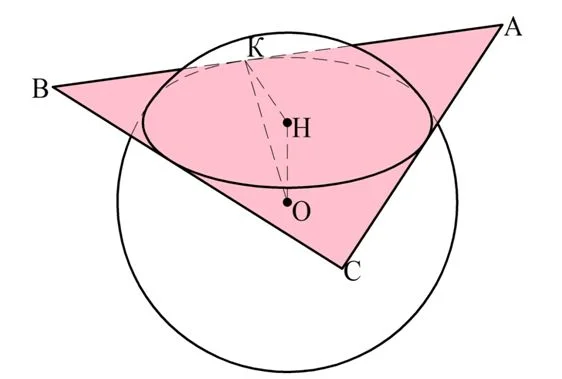
Решение. Обозначим вершины треугольника точками А, В и С. Пусть

AB = 13

AC = 14

BC = 15

Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?

Напомним одну из формул для расчета площади треугольника:

Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:

Формулы площади геометрических фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формула площади треугольника по стороне и высоте Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам
S = √p(p — a)(p — b)(p — c)
Формула площади треугольника по двум сторонам и углу между ними Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника, a, b, c — длины сторон треугольника, h — высота треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

2

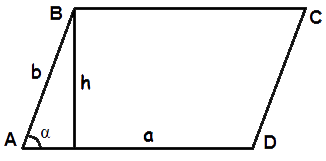
Формула площади параллелограмма по длине стороны и высоте Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними. где S — Площадь параллелограмма, a, b — длины сторон параллелограмма, h — длина высоты параллелограмма, d1, d2 — длины диагоналей параллелограмма, α — угол между сторонами параллелограмма, γ — угол между диагоналями параллелограмма.

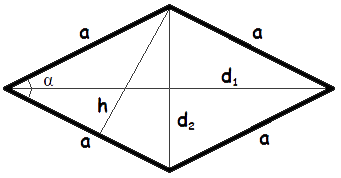
Формула площади ромба по длине стороны и высоте Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
Формула площади ромба по длине стороны и углу Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S = a2 · sin α
Формула площади ромба по длинам его диагоналей Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба, a — длина стороны ромба, h — длина высоты ромба, α — угол между сторонами ромба, d1, d2 — длины диагоналей.

Формула Герона для трапеции

S = a + b √(p-a)(p-b)(p-a-c)(p-a-d)

|a — b|
Формула площади трапеции по длине основ и высоте Площадь трапеции равна произведению полусуммы ее оснований на высоту где S — площадь трапеции, a, b — длины основ трапеции, c, d — длины боковых сторон трапеции,

p = a + b + c + d — полупериметр трапеции.

2

Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними: где S — площадь четырехугольника, d1, d2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности) Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2θ

где S — площадь четырехугольника,
- a, b, c, d — длины сторон четырехугольника,
- p = a + b + c + d2 — полупериметр четырехугольника,
- θ = α + β2 — полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p — a)(p — b)(p — c)(p — d)

Формула площади круга через радиус Площадь круга равна произведению квадрата радиуса на число пи.
S = π r2
Формула площади круга через диаметр Площадь круга равна четверти произведения квадрата диаметра на число пи. где S — Площадь круга, r — длина радиуса круга, d — длина диаметра круга.

2011-2020 Довжик МихаилКопирование материалов запрещено.

Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

Применение геометрических знаний в реальных ситуациях

Геометрия является одной из основных наук, которая имеет широкий спектр применений в реальных ситуациях. Геометрические знания позволяют решать различные задачи и проблемы, связанные с измерением, планированием и конструированием.

Архитектура и строительство

Геометрические знания необходимы в архитектуре и строительстве для создания планов зданий, расчета площадей и объемов, определения углов и размеров конструкций. Архитекторы и инженеры используют геометрию для проектирования зданий с учетом эстетических и конструктивных требований.

Навигация и геодезия

Геометрические знания играют важную роль в навигации и геодезии. Для определения местоположения точек на Земле используются геометрические методы, такие как триангуляция и трилатерация. Геодезисты используют геометрию для измерения расстояний, углов и высот, чтобы определить размеры и форму земной поверхности.

Картография

В картографии геометрические знания используются для создания и интерпретации карт. Картографы используют геометрию для проектирования картографических проекций, измерения расстояний, определения координат и создания контурных линий, которые отображают рельеф поверхности.

Дизайн и искусство

Геометрия также играет важную роль в дизайне и искусстве. Архитектура, живопись, скульптура и графический дизайн часто основаны на геометрических принципах. Формы, пропорции, углы и линии используются для создания гармоничных и эстетических композиций.

Таким образом, геометрические знания имеют широкое применение в различных областях и помогают нам лучше понять мир вокруг нас, а также решить разнообразные практические задачи, связанные с конструированием, измерением и планированием.

Пример расчета площади треугольника

Для расчета площади треугольника необходимо знать длины двух его сторон и угол между ними. Положим, у нас есть треугольник ABC, где сторона AB равна 5, сторона BC равна 6, а угол BAC равен 60 градусов.

Сначала найдем высоту треугольника. Высота проведена из вершины B к основанию AC и является перпендикулярной к основанию.

Найдем площадь треугольника ABC по формуле: S = (AB * AC * sin(BAC)) / 2. Здесь sin(BAC) — синус угла BAC.
Выразим высоту треугольника через площадь и длину основания: h = (2 * S) / AB.
Подставим известные значения и рассчитаем площадь треугольника.

Сторона AB:	5
Сторона BC:	6
Угол BAC:	60°

Расчет площади треугольника:

Выпишем формулу: S = (AB * AC * sin(BAC)) / 2.
Подставим известные значения: S = (5 * 6 * sin(60°)) / 2.
Рассчитаем синус угла BAC: sin(60°) ≈ 0.866.
Подставим значения в формулу: S = (5 * 6 * 0.866) / 2 ≈ 12.99.

Таким образом, площадь треугольника ABC составляет примерно 12.99 квадратных единиц.

Измерение углов

Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.

Относительно этих углов имеют место следующие теоремы.

Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.

Дано. Углы AOB и COD равны (черт. 109).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.

Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).

Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.

Дано. Дуги AB и CD равны (черт. 109).

Требуется доказать, что ∠AOB = ∠COD.

Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).

Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).

Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.

Даны два центральные угла AOB и COD (черт. 110).

Требуется доказать, что

AOB/COD = AB/CD.

Доказательство. Здесь имеют место два случая:

1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.

1-й случай. Дуги AB и CD соизмеримы.

Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.

Из равенств

AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE

получаем

AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).

2-й случай. Дуги AB и CD несоизмеримы.

Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.

Требуется доказать, что

AOB/AOF = AB/AF

Доказательство. A) Положим

AOB/AOF > AB/AF (1).

Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.

Положим, мы нашли, что имеет место равенство

AOB/AOF = AB/AG (a)

Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,

AOB/AOi = AB/Ai (b).

Разделив равенства (b) на (a), находим

AOF/AOi = AG/Ai

равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.

B) Допустим, что

AOB/AOF < AB/AF (2)

Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство

AOB/AOF = AB/AH (c)

Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,

AOB/AOJ = AB/AJ (d)

Разделив равенство (d) на (c) найдем

AOF/AOJ = AH/AJ

Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).

Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)

AOB/COD = AB/CD

можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.

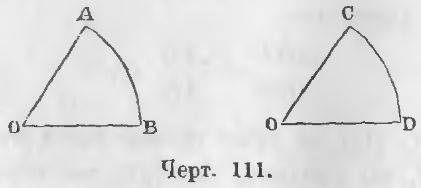
Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство

AOB/1 = AB/1

или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда

∠AOB = ◡AB.

Это равенство означает, что

числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.

p =	a + b + c	— полупериметр треугольника.
2

p =	a + b + c + d	— полупериметр трапеции.
2

S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
\|a — b\|