Онлайн калькулятор площади четырехугольника через диагонали и угол. формула

Косые четырехугольники

(Красные) боковые ребра тетрагонального дисфеноида представляют собой правильный зигзагообразный косой четырехугольник.

Неплоский четырехугольник называется косым четырехугольником . Формулы для вычисления его двугранных углов по длинам ребер и углу между двумя соседними ребрами были получены для работы над свойствами молекул, таких как циклобутан , которые содержат «морщинистое» кольцо из четырех атомов. Исторически термин « неопрятный четырехугольник » также использовался для обозначения косого четырехугольника. Косой четырехугольник вместе с его диагоналями образует (возможно, неправильный) тетраэдр и, наоборот, каждый косой четырехугольник исходит из тетраэдра, у которого удалена
пара противоположных ребер .

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

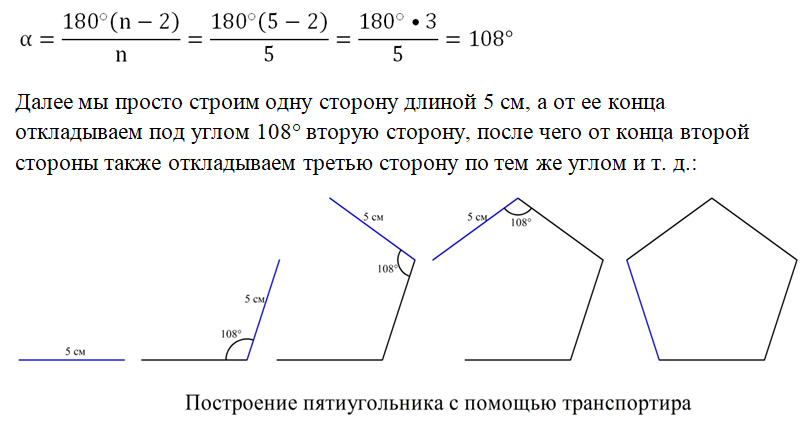
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

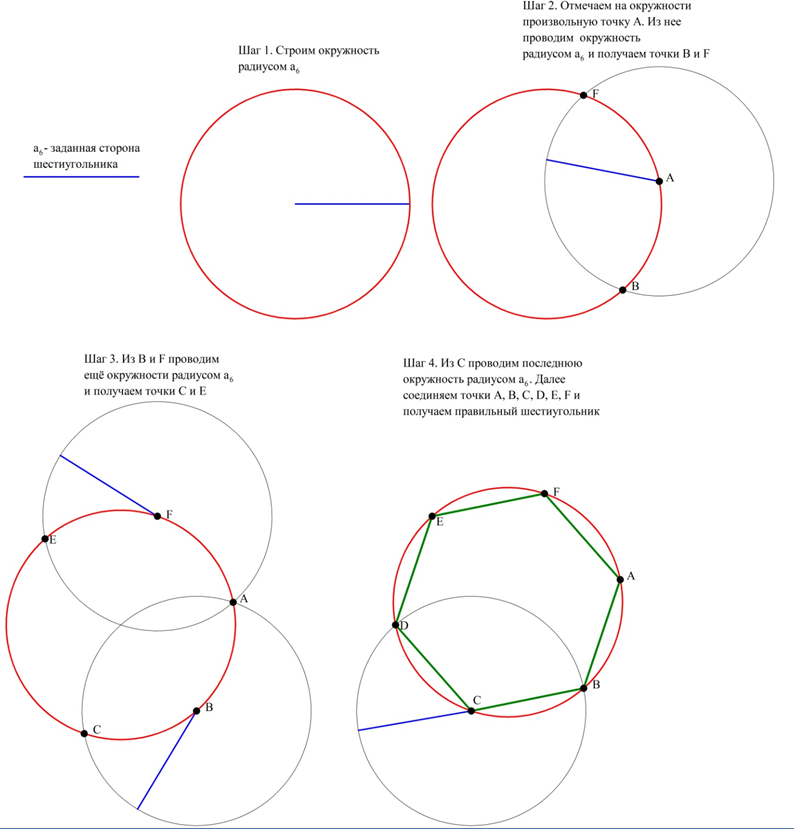
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

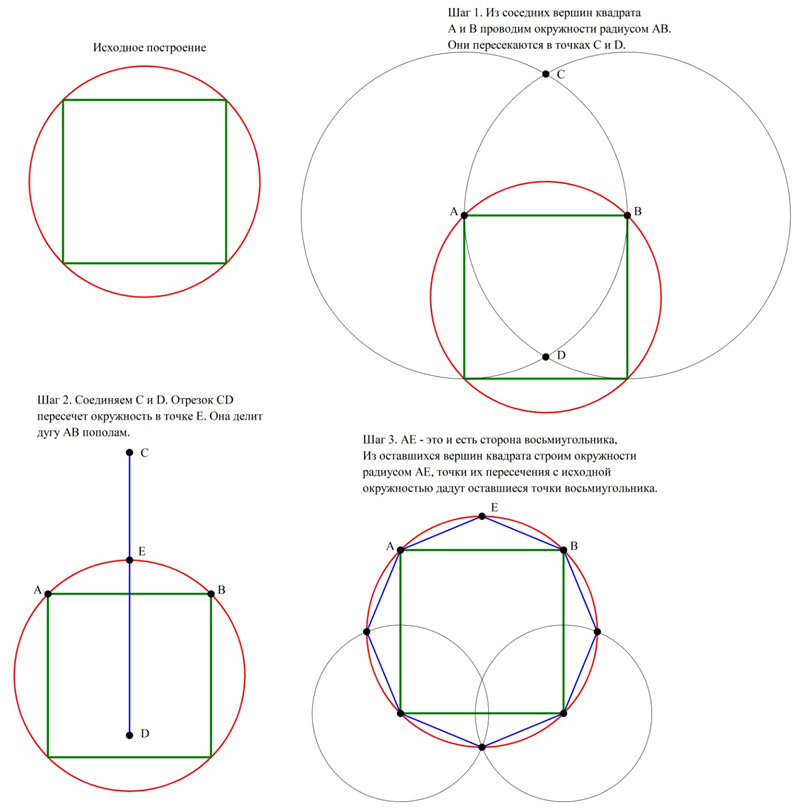
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах

Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности

Площадь фигур

Определение площади Формулы площадей фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

SEKFM = EK · EK

SEKFM = 3 · 3 = 9 см2

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

S = a2

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

SABCD = AB · BC

SABCD = 3 · 7 = 21 см2

Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

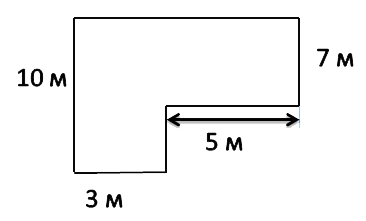
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

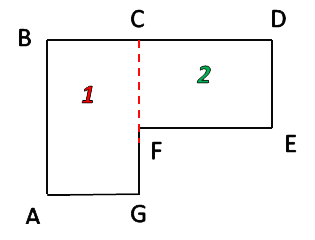SABCE = AB · BC SEFKL = 10 · 3 = 30 м2 SCDEF = FC · CD SCDEF = 7 · 5 = 35 м2

• Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников. S = SABCE + SEFKL S = 30 + 35 = 65 м2
• Ответ: S = 65 м2 — площадь огородного участка.
• Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

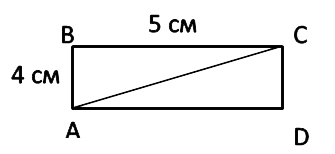
АС — диагональ прямоугольника ABCD. Найдём площадь треугольников ABC и ACD

Вначале найдём площадь прямоугольника по формуле.

SABCD = AB · BC SABCD = 5 · 4 = 20 см2

1. S ABC = SABCD : 2
2. S ABC = 20 : 2 = 10 см2
3. S ABC = S ACD = 10 см2

Площадь

Пусть длина стороны квадрата равна a, тогда формул квадрата:

S = a ⋅ a = a2

Пусть длины сторон прямоугольника равны a и b

S = a ⋅ b

Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:

S = a ⋅ ha = b ⋅ hb

Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude).
Тогда формула площади:

$S = frac{(a + b)cdot h}{2}$

$P = picdot r^2$

$pi=3,14$

$S=frac{a cdot b}{2}$

$S=frac{c cdot h_c}{2}$

Площадь треугольника — калькулятор

Стороны треугольника:

ABC — треугольник

длина его сторон: a, b, c и длина его высот: ha, hb и hc.

S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)

S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)

• p = ½(a + b + c)
• S = √p(p — a)(p — b)(p — c) — формула Герона
• $S = R^2sin(A) cdot sin(B) cdot sin(C) = frac{abc}{4R}$

где R — радиус описанной окружности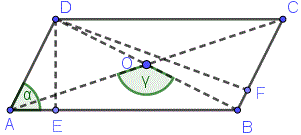

1. $S = ABcdot DE = BC cdot DF$
   $S = AB cdot AD sin alpha$
2. $S = frac12 AC cdot BD sin gamma$

$S = frac12 AC cdot BD sin varphi $

Как найти площадь прямоугольника с разными сторонами. Площадь прямоугольника — это?

Площадь прямоугольника — это измерения, по которым вычисляемая площадь неправильного четырехугольника, вписанного в него. Как найти площадь прямоугольника с разными сторонами? Для этого нужно знать длину двух его сторон, а именно длину основания и высоту.

Если значения основания и высоты измеряются в разных единицах, то перед вычислением площади нужно привести их к одной системе. Например, если одно измерение дано в метрах, а другое в сантиметрах, необходимо привести все к одной системе, например, к метрам.

Площадь прямоугольника может быть выражена в квадратных единицах (например, квадратных метрах), так как это мера площади. Используя расчетную формулу, как показал индийский математик Брахмагупта, можно легко найти площадь прямоугольника с разными сторонами и получить точный результат.

Примеры задач на нахождение площади трапеции

Задача 1

Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

Решение

Для решения задачи воспользуемся .

S = \dfrac{1}{2} (a + b) \cdot h = \dfrac{1}{2} (6 + 9) \cdot 5 = \dfrac{1}{2} \cdot 15 \cdot 5 = \dfrac{1}{2} \cdot 75 = 37\dfrac{1}{2} \: см^2

Ответ: 37.5 см²

Полученный ответ легко проверить с помощью .

Задача 2

Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.

Решение

С решением этой задачи нам поможет .

S = m \cdot h = 18 \cdot 9 = 162 \: см^2

Ответ: 162 см²

Воспользуемся для проверки результата.

Задача 3

Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.

Решение

Для решения этой задачи нам поможет .

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{10+8+2 \cdot 3}{2} = \dfrac{10+8+6}{2} = \dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{12(12-10)(12-8)(12-2 \cdot 3)} = \sqrt{12 \cdot 2 \cdot 4 \cdot 6} = \sqrt{576} = 24 \: см^2

Ответ: 24 см²

Осталось полученный ответ.

Задача 4

Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.

Решение

Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{17+15+ 2 \cdot 4}{2} = \dfrac{17+15+8}{2} = \dfrac{40}{2} = 20

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{20(20-17)(20-15)(20-2 \cdot 4)} = \sqrt{20 \cdot 3 \cdot 5 \cdot 12} = \sqrt{3600} = 60 \: см^2

Ответ: 60 см²

Задача 5

Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.

Решение

Еще одна типовая задача. Повторим действия как в задачах выше.

На первом этапе вычислим p:

p = \dfrac{d_1+d_2+2m}{2} = \dfrac{8+6+ 2 \cdot 5}{2} = \dfrac{8+6+10}{2} = \dfrac{24}{2} = 12

А теперь можно вычислить площадь трапеции:

S = \sqrt{p(p-d_1)(p-d_2)(p-2m)} = \sqrt{12(12-8)(12-6)(12-2 \cdot 5)} = \sqrt{12 \cdot 4 \cdot 6 \cdot 2} = \sqrt{576} = 24 \: см^2

Ответ: 24 см²

Задача 6

Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.

Решение

Для решения этой задачи используем .

Сначала вычислим p:

p = \dfrac{a+b+2c}{2} = \dfrac{5+17+2 \cdot 10}{2} = \dfrac{22+20}{2} = \dfrac{42}{2} = 21

А теперь можно вычислить площадь трапеции:

S = \sqrt{(p-a)(p-b)(p-c)^2} = \sqrt{(21-5)(21-17)(21-10)^2} = \sqrt{16 \cdot 4 \cdot 11^2} = \sqrt{16 \cdot 4 \cdot 121} = \sqrt{7744}= 88 \: см^2

Ответ: 88 см²

Задача 7

Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.

Решение

Для решения этой задачи воспользуемся .

S = \dfrac{1}{2}(b^2-a^2) \cdot \tg(\alpha) = \dfrac{1}{2}(8^2-6^2) \cdot \tg(45°)

Тангенс 45° = 1, продолжим вычисления:

S = \dfrac{1}{2}(8^2-6^2) \cdot \tg(45°) = \dfrac{1}{2}(64-36) \cdot 1 = \dfrac{1}{2} \cdot 28 = 14 \: см^2

Ответ: 14 см²

Убедиться в правильности решения нам поможет .

Формула вычисления площади

По диагоналям и углу между ними

Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.

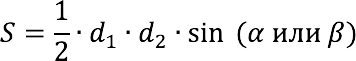
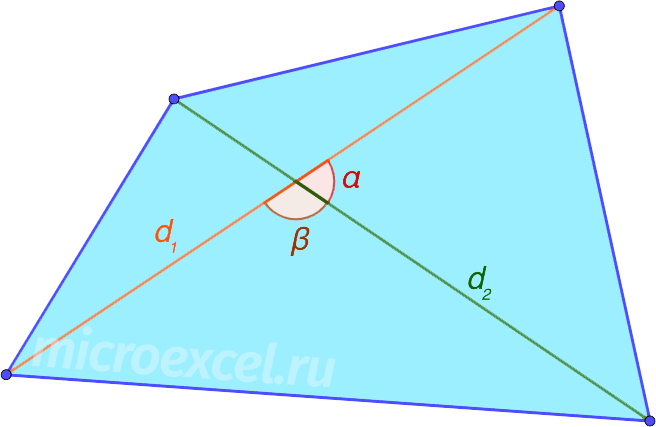
По четырем сторонам (формула Брахмагупты)

Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.

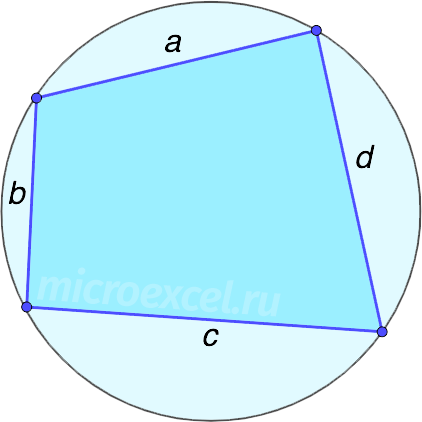
p – полупериметр, вычисляется следующим образом:

По радиусу вписанной окружности и сторонам

Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:

S = p ⋅ r

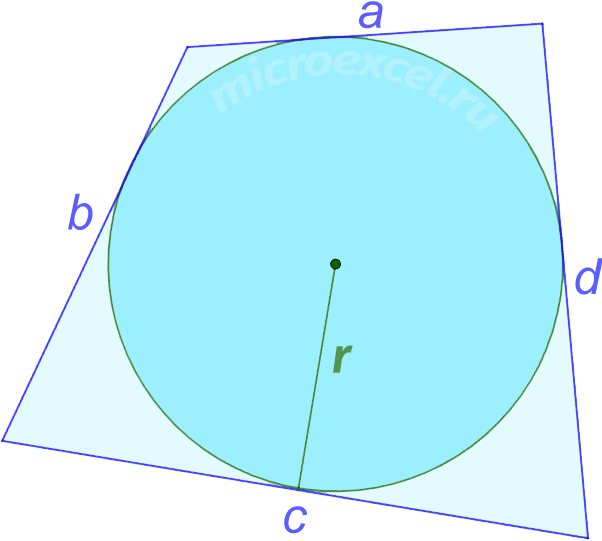
r – радиус окружности.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

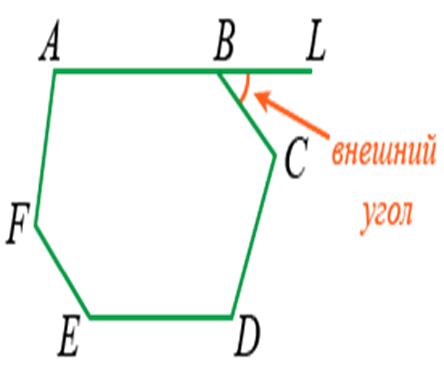
Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

• сумма углов – s;
• число сторон – n;
•  два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

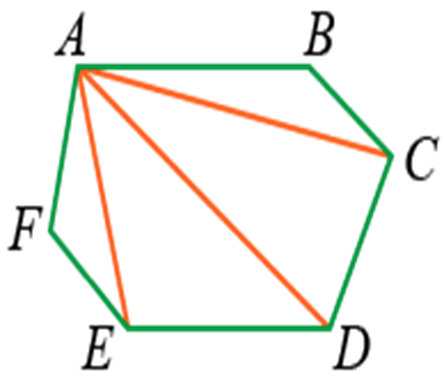
Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Нахождение площади четырёхугольника различными способами и методами

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).

Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.

Теперь пусть даны стороны и противолежащие углы четырёхугольника.

Пусть a, b, c, d известные стороны многоугольника; p — его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).

На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.

Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.

Подставим полученные данные в нашу формулу, получим: S = rad((40 — 18)*(40 — 23)*(40 — 22)*(40 — 17) — 18*23*22*17*0,97) = rad(22*17*18*23 — 18*23*22*17*1/4) = rad((22*17*18*23*(1 — 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.

Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.

Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:

S = ((a + b+ c + d)/2)*r

Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:

S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.

Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.

Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:

S = rad((65 — 26)*(65 — 35)*(65 — 39)*(65 — 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.

Тригонометрические тождества

Четыре угла простого четырехугольника ABCD удовлетворяют следующим тождествам:

грех⁡А+грех⁡Б+грех⁡С+грех⁡Дзнак равно4грех⁡А+Б2грех⁡А+С2грех⁡А+Д2{\ displaystyle \ sin {A} + \ sin {B} + \ sin {C} + \ sin {D} = 4 \ sin {\ frac {A + B} {2}} \ sin {\ frac {A+ C}{2}}\sin {\frac {A+D}{2}}}

и

загар⁡Азагар⁡Б−загар⁡Сзагар⁡Дзагар⁡Азагар⁡С−загар⁡Бзагар⁡Дзнак равнозагар⁡(А+С)загар⁡(А+Б).{\ displaystyle {\ frac {\ tan {A} \ tan {B} — \ tan {C} \ tan {D}} {\ tan {A} \ tan {C} — \ tan {B} \ tan {D }}} = {\ frac {\ tan {(A + C)}} {\ tan {(A + B)}}}}.}

Также,

загар⁡А+загар⁡Б+загар⁡С+загар⁡Ддетская кроватка⁡А+детская кроватка⁡Б+детская кроватка⁡С+детская кроватка⁡Дзнак равнозагар⁡Азагар⁡Бзагар⁡Сзагар⁡Д.{\ displaystyle {\ frac {\ tan {A} + \ tan {B} + \ tan {C} + \ tan {D}} {\ кроватка {A} + \ кроватка {B} + \ кроватка {C} + \cot {D}}}=\загар {A}\загар {B}\загар {C}\загар {D}.}

В последних двух формулах ни один угол не может быть прямым , так как tan 90° не определен.

Пусть , , , — стороны не перекрестного четырехугольника, — полупериметр, и — противоположные углы, тогда
а{\ Displaystyle а}б{\ Displaystyle б}с{\ Displaystyle с}д{\ Displaystyle д}с{\ Displaystyle с}А{\ Displaystyle А}С{\ Displaystyle С}

адгрех2⁡А2+бспотому что2⁡С2знак равно(с−а)(с−д){\ displaystyle ad \ sin ^ {2} {\ frac {A} {2}} + bc \ cos ^ {2} {\ frac {C} {2}} = (sa) (sd)}

и

бсгрех2⁡С2+адпотому что2⁡А2знак равно(с−б)(с−с){\ displaystyle bc \ sin ^ {2} {\ frac {C} {2}} + ad \ cos ^ {2} {\ frac {A} {2}} = (sb) (sc)}.

Мы можем использовать эти тождества для вывода формулы Бретшнайдера .

Как найти площадь геометрических фигур?

Что такое площадь?

Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).

1. Самая известная формула площади треугольника по стороне и высоте:

S = a · h

где a – длина основания, h  – высота треугольника, проведенная к основанию.

Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.

Если треугольник тупоугольный, то высота опускается на продолжение основания:

Если треугольник прямоугольный, то основанием и высотой являются его катеты:

2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:

S =   a · b · sinα  

где a и b – две стороны треугольника,  sinα  – синус угла между этими сторонами.

• Главное условие – угол берется между двумя известными сторонами.
• 3. Формула площади по трем сторонам (формула Герона):

S =  

где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.

4. Формула площади треугольника через радиус описанной окружности:

S =  

где a, b и с – стороны треугольника, а R – радиус описанной окружности.

5. Формула площади треугольника через радиус вписанной окружности:

S =p · r

где р – полупериметр треугольника, а r – радиус вписанной окружности.

1. Площадь прямоугольника находится довольно-таки просто:

S = a · b

Никаких подвохов.

1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:

S = a · a = a2

2. Также площадь квадрата можно найти через его диагональ:

S =   d2

1. Площадь параллелограмма находится по формуле:

S = a · h

1. Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. 2. Также площадь параллелограмма можно найти через угол между двумя сторонами:

S = a · b · sinα

Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.

1. Площадь ромба через высоту:

S = a · h

1. Площадь трапеции находится по следующей формуле:

S =   · h 

Максимальные и минимальные свойства

Среди всех четырехугольников с данным периметром наибольшей площадью является квадрат . Это называется изопериметрической теоремой для четырехугольников . Это прямое следствие неравенства площадей

К≤116л2{\ displaystyle K \ leq {\ tfrac {1} {16}} L ^ {2}}

где K — площадь выпуклого четырехугольника с периметром L. Равенство выполняется тогда и только тогда , когда четырехугольник является квадратом. Двойственная теорема утверждает, что из всех четырехугольников с заданной площадью наименьший периметр имеет квадрат.

Четырехугольник с заданными длинами сторон, имеющий максимальную площадь, называется вписанным четырехугольником .

Из всех выпуклых четырехугольников с заданными диагоналями ортогональный четырехугольник имеет наибольшую площадь. Это прямое следствие того, что площадь выпуклого четырехугольника удовлетворяет условию

Кзнак равно12пдгрех⁡θ≤12пд,{\ displaystyle K = {\ tfrac {1} {2}} pq \ sin {\ theta} \ leq {\ tfrac {1} {2}} pq,}

где θ — угол между диагоналями p и q . Равенство имеет место тогда и только тогда, когда θ = 90°.

Если P — внутренняя точка выпуклого четырехугольника ABCD , то

Ап+Бп+Сп+Дп≥АС+БД.{\ displaystyle AP + BP + CP + DP \ geq AC + BD.}

Из этого неравенства следует, что точка внутри четырехугольника, минимизирующая сумму расстояний до вершин , есть пересечение диагоналей. Следовательно, эта точка является точкой Ферма выпуклого четырехугольника.

Как найти площадь неправильного четырехугольника?

Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение. 

Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

Как описать четырехугольник окружностью?

Окружность, проходящая по всем вершинам четырехугольника, называется описанной окружностью. Если сумма противоположных углов равна 180°, то такой четырехугольник можно описать окружностью. В случае, если данное условие не выполняется, то такой четырехугольник невозможно описать окружностью.

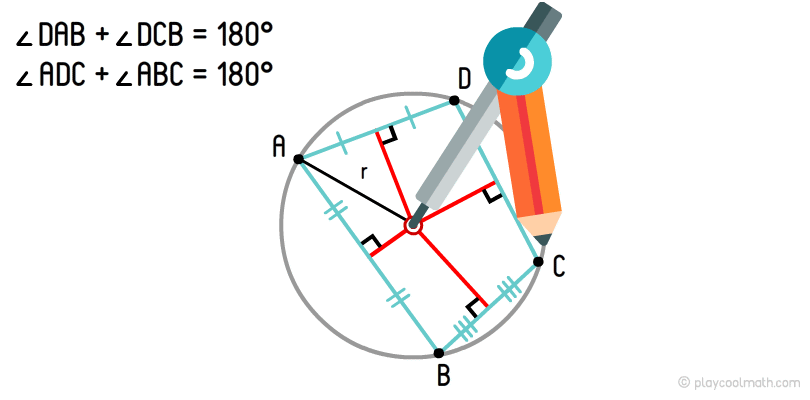Центр описанной окружности четырехугольника — это точка пересечения перпендикуляров, выходящих из середины сторон.

Мы уже рисовали описанную окружность для треугольника. Алгоритм для описания окружности для четырехугольника такой же. На рисунке хорошо видно, как из середины сторон мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность четырехугольника.

Найди ортодиагональные четырехугольники.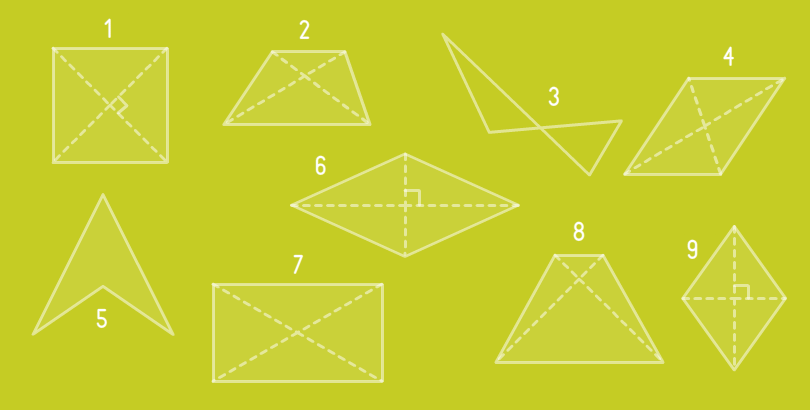

• #1
• #6
• #9

Вычисление объемов фигур

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Базовая информация

Объем геометрической фигуры — это количественная характеристика пространства, которое занимает тело. Она определяется его формой и размерами. Чтобы задачи на вычисление объемов геометрических фигур не вызывали затруднений, рекомендуем освежить в памяти основные формулы.

• Объем куба равняется кубу длины его грани.

Для его расчета используется формула: V = a3, где V — объем куба, a — длина его грани.

Объем призмы равняется произведению площади основания фигуры на высоту. Чтобы его рассчитать, воспользуйтесь следующий формулой: V = So h, где V — объем призмы, So — площадь ее основания, h — ее высота.
Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты. Формула для его расчета: V = a · b · h, где a — длина, b — ширина, h — высота.
Объем пирамиды равняется трети от произведения площади ее основания на высоту.

Рассчитать его можно по формуле: V = 1/3 So· h , где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.

Объем цилиндра равняется произведению площади его основания на высоту. Формулы для его расчета:

V = π R2 h V = So h

Где V — объем цилиндра, So — площадь основания цилиндра, R — радиус цилиндра, h — высота цилиндра, π = 3.141592.

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Общие сведения

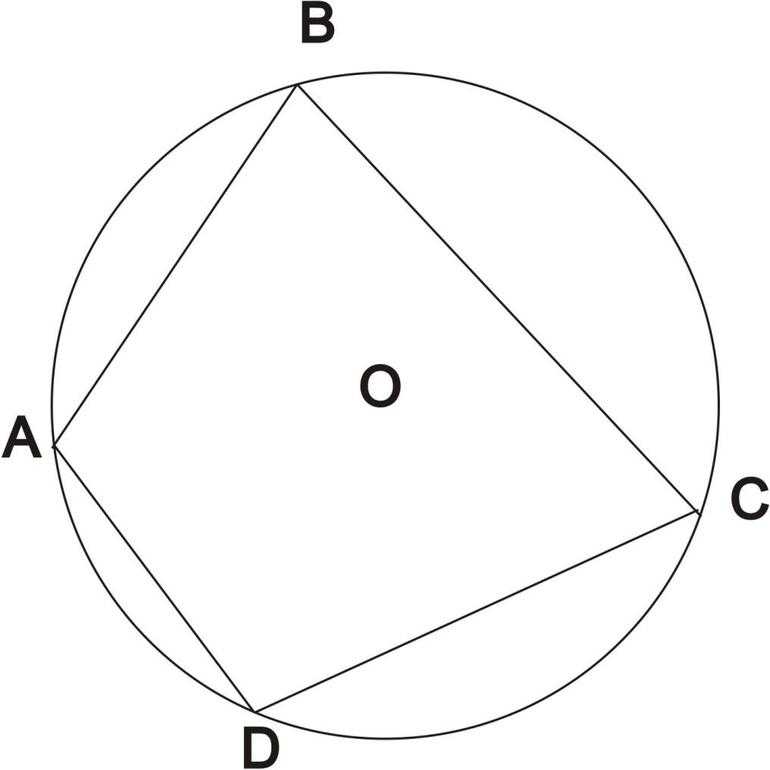
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.

Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.

Основные правила

Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:

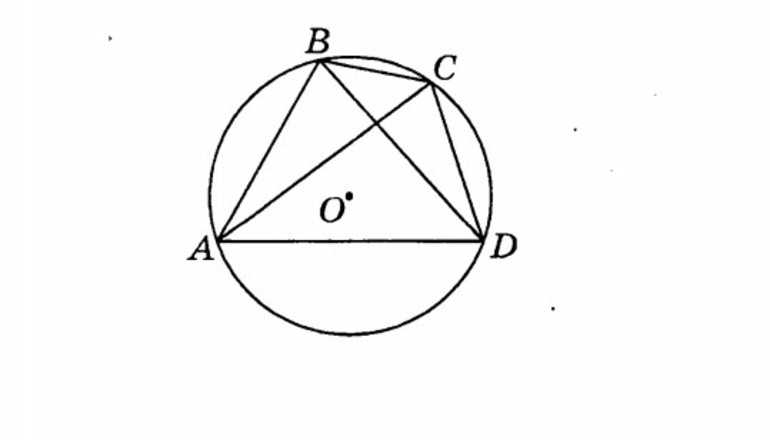
• Сумма углов, которые являются противоположными, соответствует 180 градусам.
• Соблюдается равенство смежного и противоположного углов.
• Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
• Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
• Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
• Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).

Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.

Свойства и утверждения

При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:

• Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
• Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
• При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.

Методы вычисления площади разностороннего четырехугольника

Метод 1: Разбиение на треугольники

• Этот метод заключается в разбиении четырехугольника на два треугольника и вычислении площади каждого из них по формуле S = (a+b+c)/2 * p, где a, b, c — стороны треугольника, p — полупериметр.
• После этого площадь четырехугольника будет равна сумме площадей этих двух треугольников.

Метод 2: Использование диагоналей

• В этом методе необходимо найти длину обеих диагоналей четырехугольника и угол между ними.
• Площадь можно вычислить по формуле S = 0.5 * d1 * d2 * sin(угол), где d1 и d2 — длины диагоналей, sin(угол) — синус угла между диагоналями.

Метод 3: Формула Брезенхема

• Этот метод хорошо подходит для расчета площади не только четырехугольников, но и других сложных многоугольников.
• В основе формулы Брезенхема лежит широко известный алгоритм, используемый для рисования линий на экране.
• Этот метод позволяет вычислить площадь любого многоугольника, используя его вершины и длины его сторон.

Сложные четырехугольники

антипараллелограмм

Самопересекающийся четырехугольник называется по-разному перекрестным четырехугольником , скрещенным четырехугольником , четырехугольником — бабочкой или четырехугольником с галстуком-бабочкой . В скрещенном четырехугольнике четыре «внутренних» угла по обе стороны от пересечения (два острых и два отраженных , все слева или все справа, как показано на рисунке) составляют в сумме 720 °.

• (США) или трапеция (Содружество): скрещенный четырехугольник, в котором одна пара несмежных сторон параллельна (как у трапеции ) .
• Антипараллелограмм : скрещенный четырехугольник, в котором каждая пара несмежных сторон имеет одинаковую длину (как параллелограмм ) .
• Перекрещенный прямоугольник : антипараллелограмм, стороны которого являются двумя противоположными сторонами и двумя диагоналями прямоугольника , следовательно, имеет одну пару параллельных противоположных сторон.
• : частный случай скрещенного прямоугольника, две стороны которого пересекаются под прямым углом.

Неравенства

Площадь

Если выпуклый четырехугольник имеет последовательные стороны a , b , c , d и диагонали p , q , то его площадь K удовлетворяет условию

К≤14(а+с)(б+д){\ Displaystyle К \ leq {\ tfrac {1} {4}} (а + с) (б + г)}с равенством только для прямоугольника .

К≤14(а2+б2+с2+д2){\ displaystyle K \ leq {\ tfrac {1} {4}} (a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2})}с равенством только для квадрата .

К≤14(п2+д2){\ displaystyle K \ leq {\ tfrac {1} {4}} (p ^ {2} + q ^ {2})}с равенством, только если диагонали перпендикулярны и равны.

К≤12(а2+с2)(б2+д2){\ displaystyle K \ leq {\ tfrac {1} {2}} {\ sqrt {(a ^ {2} + c ^ {2}) (b ^ {2} + d ^ {2})}}}с равенством только для прямоугольника.

Из формулы Бретшнайдера прямо следует, что площадь четырехугольника удовлетворяет условию

К≤(с−а)(с−б)(с−с)(с−д){\ displaystyle K \ leq {\ sqrt {(sa) (sb) (sc) (sd)}}}

с равенством тогда и только тогда , когда четырехугольник циклический или вырожденный, так что одна сторона равна сумме трех других (он схлопнулся в отрезок , поэтому площадь равна нулю).

Площадь любого четырехугольника также удовлетворяет неравенству

К≤12(аб+сд)(ас+бд)(ад+бс)3.{\ displaystyle \ displaystyle K \ leq {\ tfrac {1} {2}} {\ sqrt {(ab + cd) (ac + bd) (ad + bc)}}.}

Обозначая периметр как L , имеем

К≤116л2,{\ Displaystyle К \ Leq {\ tfrac {1} {16}} L ^ {2},}

с равенством только в случае квадрата.

Площадь выпуклого четырехугольника также удовлетворяет

К≤12пд{\ displaystyle K \ leq {\ tfrac {1} {2}} pq}

для длин диагоналей p и q с равенством тогда и только тогда, когда диагонали перпендикулярны.

Пусть a , b , c , d — длины сторон выпуклого четырехугольника ABCD площади K и диагоналей AC = p , BD = q . потом

К≤а2+б2+с2+д2+п2+д2+пд−ас−бд8{\ displaystyle K \ leq {\ frac {a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2} + p ^ {2} + q ^ {2} + pq-ac- бд{8}}}с равенством только для квадрата.

Пусть a , b , c , d — длины сторон выпуклого четырехугольника ABCD площади K , тогда выполняется следующее неравенство:

К≤13+3(аб+ас+ад+бс+бд+сд)−12(1+3)2(а2+б2+с2+д2){\ displaystyle K \ leq {\ frac {1} {3 + {\ sqrt {3}}}} (ab + ac + ad + bc + bd + cd) — {\ frac {1} {2 (1+ { \sqrt {3}})^{2}}}(a^{2}+b^{2}+c^{2}+d^{2})}с равенством только для квадрата.

Диагонали и бимедианы

Следствием теоремы Эйлера о четырехугольнике является неравенство

а2+б2+с2+д2≥п2+д2{\ displaystyle a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2} \ geq p ^ {2} + q ^ {2}}

где равенство выполняется тогда и только тогда, когда четырехугольник является параллелограммом .

Эйлер также обобщил теорему Птолемея , которая представляет собой равенство во вписанном четырехугольнике , в неравенство для выпуклого четырехугольника. В нем говорится, что

пд≤ас+бд{\ Displaystyle pq \ leq ac + bd}

где равенство имеет место тогда и только тогда , когда четырехугольник вписанный. Это часто называют неравенством Птолемея .

В любом выпуклом четырехугольнике бимедианы m, n и диагонали p, q связаны неравенством

пд≤м2+н2,{\ Displaystyle pq \ leq м ^ {2} + п ^ {2},}

с равенством тогда и только тогда, когда диагонали равны. Это следует непосредственно из четырехугольного тождествам2+н2знак равно12(п2+д2).{\ displaystyle m ^ {2} + n ^ {2} = {\ tfrac {1} {2}} (p ^ {2} + q ^ {2}}.}

Стороны

Стороны a , b , c и d любого четырехугольника удовлетворяют

а2+б2+с2>д23{\ displaystyle a ^ {2} + b ^ {2} + c ^ {2}> {\ frac {d ^ {2}} {3}}}

и

а4+б4+с4≥д427.{\ displaystyle a ^ {4} + b ^ {4} + c ^ {4} \ geq {\ frac {d ^ {4}} {27}}.}

Как найти площадь четырехугольника — дельтоида

Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:

• Известны стороны фигуры и угол, образованный сторонами разной длины:
  S = m*l*sinϕ,
  m, l – стороны дельтоида,
  ϕ – угол между ними.
• Известны стороны фигуры и углы, образованные сторонами равной длины:
  S = m 2 *sinα/2 + l 2 *sinβ/2,
  m, l – стороны дельтоида,
  α, β — углы между равными сторонами.
• Наличие известных диагоналей также позволяет определить площадь фигуры:
  S = d1*d2/2,
  d1, d2 – диагонали дельтоида.
• Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
  m, l – стороны дельтоида,
  r – радиус в случае вписанной окружности.

Заключение

Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов — квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:

1. S = 1/2*d1*d2*sin(d1,d2);
2. S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
3. S = ((a + b+ c + d)/2)*r

S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра​.

Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.