Геометрическая фигура призма: виды, свойства, элементы

Вычисление объема

Рассмотрим произвольную призму из числа прямых, правильных или наклонных. Представим изображение на рисунке и обозначим все компоненты такого геометрического объекта.

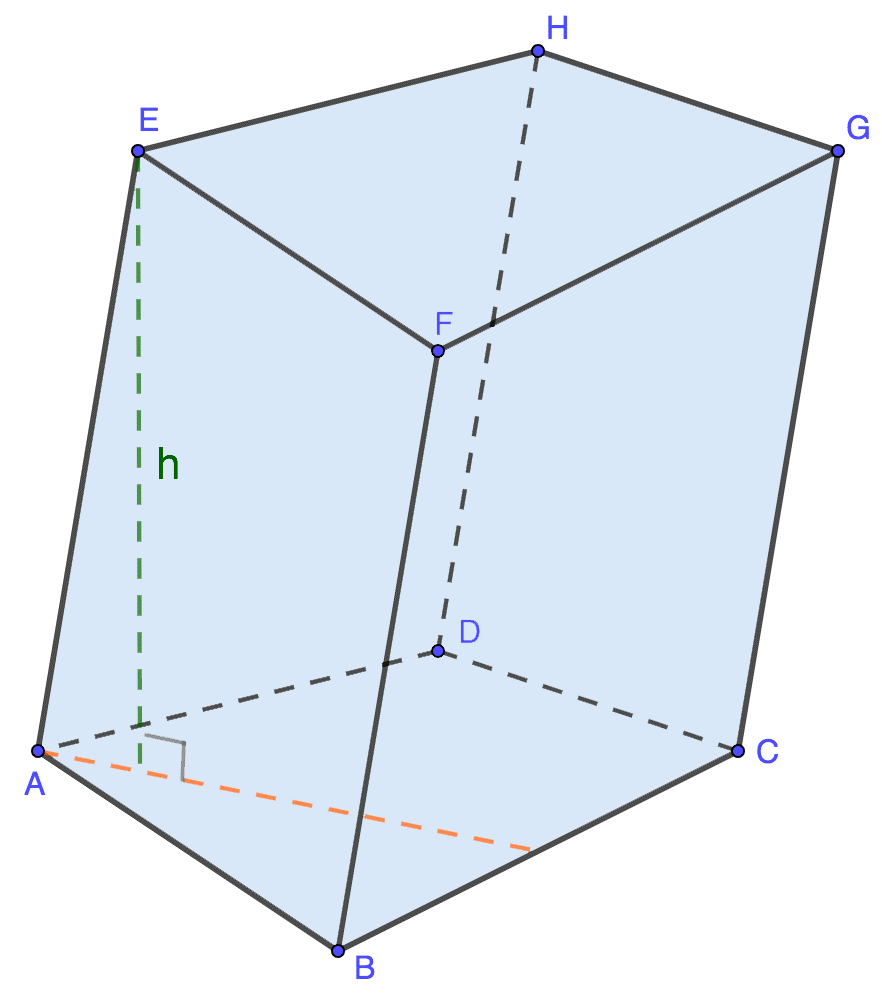
Вычислить, чему равен объем такой призмы, можно с помощью следующей формулы:

\(V = S_{осн} \cdot h\)

Таким образом, для определения объема геометрического объекта, обладающего всеми признаками любой из перечисленных выше разновидностей призмы, следует найти результат от умножения площади основания и высоты фигуры. С целью расчета первого параметра необходимо рассмотреть многоугольник с четырьмя углами, который обозначен на рисунке за ABCD или EFGH.

Четырехугольная призма

Ее основанием является любой из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В каждом случае для того, чтобы вычислить площадь основания призмы, будет нужна своя формула.

Если основание — прямоугольник, то его площадь определяется так: S = ав, где а, в — стороны прямоугольника.

Когда речь идет о четырехугольной призме, то площадь основания правильной призмы вычисляется по формуле для квадрата. Потому что именно он оказывается лежащим в основании. S = а 2 .

В случае когда основание — это параллелепипед, будет нужно такое равенство: S = а * н а. Бывает такое, что даны сторона параллелепипеда и один из углов. Тогда для вычисления высоты потребуется воспользоваться дополнительной формулой: н а = в * sin А. Причем угол А прилегает к стороне «в», а высота н а противолежащая к этому углу.

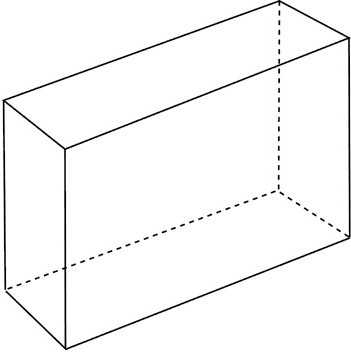
Параллелепипед и куб

Призму, основаниями которой являются параллелограммы, называют параллелепипедом (рис. 27). Параллелепипеды, как и призмы, могут быть прямыми (рис. 27.а) и наклонными (рис. 27.б).

Поверхности параллелепипеда, не имеющие общей вершины, называются противоположными поверхностями.

Для параллелепипеда:

• -12 ребер, каждые четыре из которых равны (рис. 28.а),
• -6 параллельных и равных попарно поверхностей (рис. 28.б),
• -4 диагонали, которые пересекаются и точка пересечения делится надвое (рис. 28.в),
• — пересечение диагоналей является центром его симметрии (рис. 28.в). Прямой параллелепипед имеет ось симметрии (рис. 28.г) и плоскость симметрии (рис. 28.д).

Прямоугольный параллелепипед, основаниями которого являются прямоугольники, называется прямоугольным параллелепипедом (рис. 29). Ясно, что все грани прямоугольного параллелепипеда — прямоугольники.

Прямоугольный параллелепипед имеет три оси симметрии (рис. 30) и три плоскости симметрии (рис. 31).

Длина трех ребер, выходящих из одной вершины прямоугольного параллелепипеда, называется его размерами.

Свойство: В прямоугольном параллелепипеде квадрат любой диагонали d равен сумме квадратов его размеров: а, b и с (рис. 32):

.

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Ясно, что все грани куба равные квадраты. Куб имеет один центр симметрии, 9 осей симметрии и 9 плоскостей симметрии.

Свойства призмы перечислены выше. Некоторые из них были показаны в 10-м классе. Доказательства остальных свойств проще, поэтому их можно выполнить самостоятельно.

Формулы вычисления объема и площади поверхности призмы:

Для наглядности формул введем обозначения:

$P_{base}$ — периметр основания;

$S_{base}$ — базовая площадь;

$S_{side}$ — площадь боковой поверхности;

$S_{pp}$ — общая площадь поверхности;

$h$ — высота призмы.

$S_{сторона}=P_{основная} ч$

$S_{pp}=S_{сторона}+2S_{основная}$

$V=S_{первичный} ч$

В основании призмы могут лежать разные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

1. $S={a h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $a$
2. $S={a·b·sin⁡α}/{2}$, где $a,b$ — смежные стороны, $α$ — угол между этими смежными сторонами.
3. Формула Герона $S=√{p(pa)(pb)(pc)}$, где $p$ — полупериметр $p={a+b+c}/{2}$
4. $S=pr$, где $r$ — радиус вписанной окружности
5. $S={abc}/{4R}$, где $R$ — радиус описанной окружности
6. Для прямоугольного треугольника $S={ab}/{2}$, где $a$ и $b$ — катеты прямоугольного треугольника.

2. Ромб

$S={d_1 d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $a$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

3. Трапеция

$S={(a+b)·h}/{2}$, где $a$ и $b$ — основания трапеции, $h$ — высота трапеции.

Прямая призма называется правильной, если ее основания — правильные многоугольники.

Площадь поверхности призмы

После того, как сформировано понимание об основных элементах призмы и ее разновидностях, целесообразно перейти непосредственно к способам вычисления параметров геометрической фигуры. Стоит начать изучение с формул для выполнения расчетов и математических соотношений, которые предназначены для определения площади поверхности объекта. Запишем общую формулировку для вычисления площади полной поверхности геометрической фигуры:

\(S_{общ} = S_{бок} + 2S_{осн}\)

Если призма является прямой, то определить площадь боковой поверхности такой фигуры несложно, зная периметр основания и величину высоты:

\(S_{бок} = Р_{осн}\cdot h\)

Далее запишем математические соотношения, выражающие закономерности между элементами правильной треугольной призмы, в основании которой лежит равносторонний треугольник:

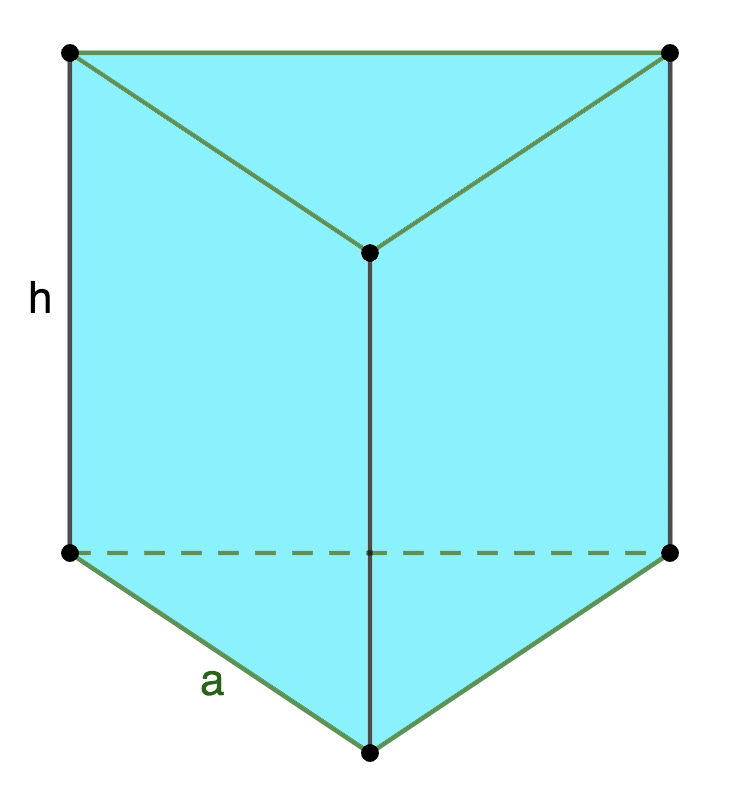
\(S_{осн} = \frac{a^{2}\sqrt{3}}{4}\)

\(S_{бок} = 3аh\)

\(S_{полн} = 3аh + 2\frac{a^{2}\sqrt{3}}{4} = \frac{a^{2}\sqrt{3} + 6аh}{2}\)

Если в задании по геометрии на расчет площади поверхности призмы речь идет о правильной четырехугольной фигуре с квадратом в основании, то целесообразно воспользоваться следующими формулами. Представим изображение такого геометрического объекта с соответствующими обозначениями и сопроводим рисунок несколькими полезными формулами.

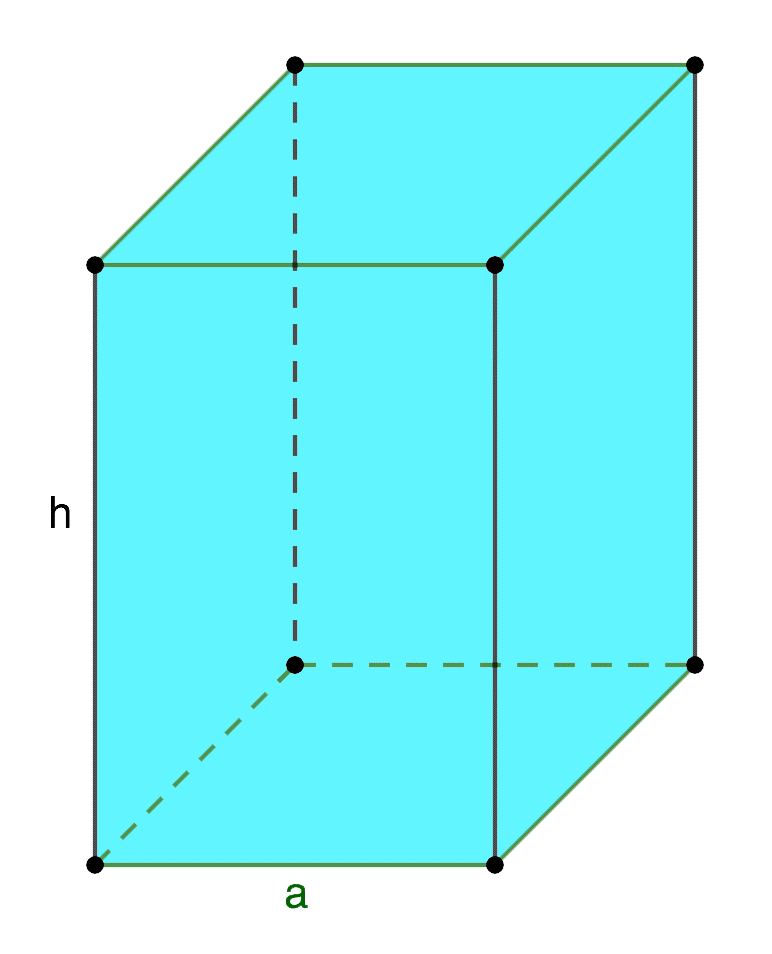
\(S_{осн} = a^{2}\)

\(S_{бок} = 4аh\)

\(S_{полн} = 2a^{2}+ 4аh\)

Рассмотрим следующий случай, который часто встречается в примерах по геометрии. Речь идет о правильной шестиугольной призме, основание которой представлено в виде правильного многоугольника с шестью углами.

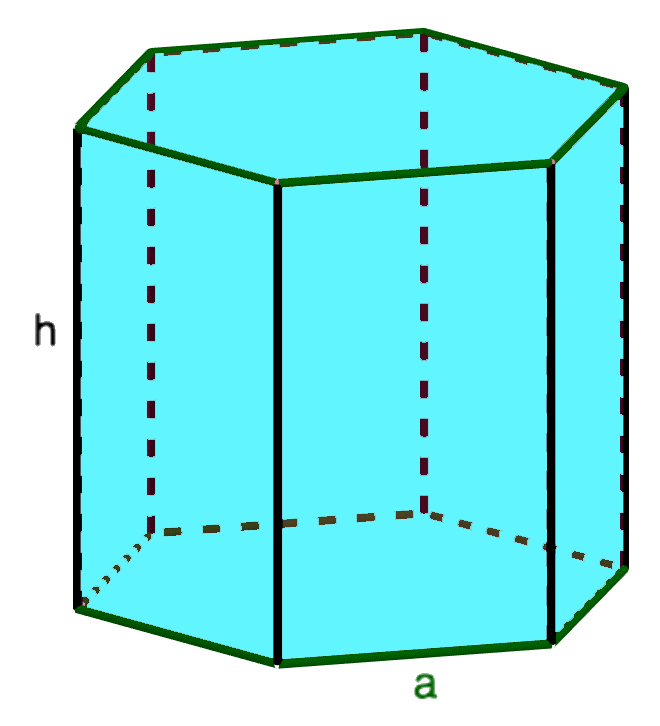
\(S_{осн} = \frac{3\sqrt{3}a^{2}}{2}\)

\(S_{бок} = 6аh\)

\(S_{полн} = 6аh + 2\frac{3\sqrt{3}a^{2}}{2} = 6аh + 3\sqrt{3}a^{2}\)

Виды призм

В зависимости от количества углов в основании призмы ее можно назвать треугольной, квадратной и т д. (рис. 2).

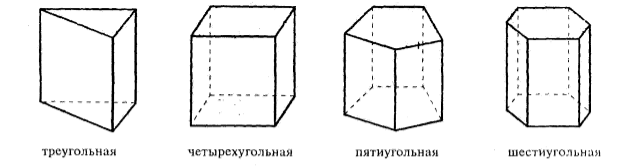
Фигура 2.

Английский для начинающих Не откладывайте свои мечты на потом – начните общение с опытным преподавателем Узнать больше

Обратите внимание, что параллелепипед — это частный случай квадратной призмы. Определение 2

Определение 2

Призму, у которой все двугранные углы равны ${90}^0$, называют прямой призмой (рис. 3). В противном случае он наклонен.

Рисунок 3. Прямая призма

Определение 3

Прямая призма, основанная на правильных $n-$угольниках, называется правильной призмой (рис. 4).

Рисунок 4

Элементы

Перед тем, как приступить к разбору и решению геометрических задач, следует разобраться с терминологией. Введем понятия для всех основных компонентов призмы. Сделать это целесообразно, используя рисунок, представленный ниже:

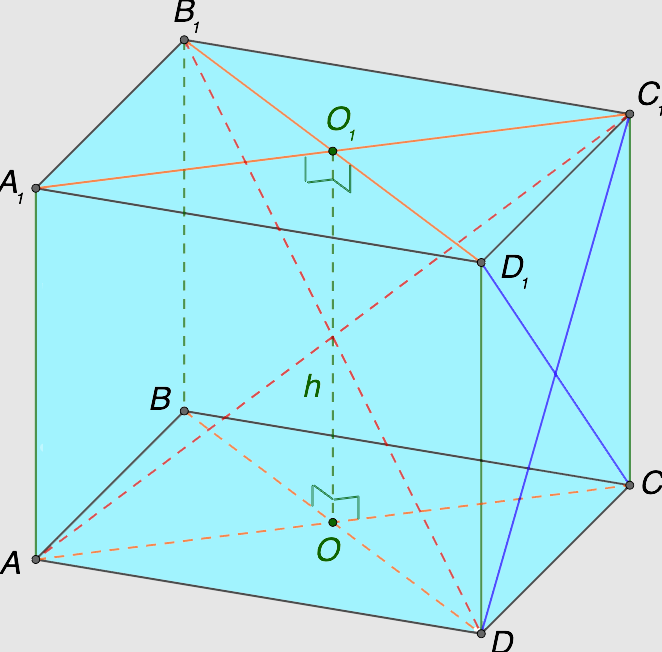
Перечислим элементы геометрического объекта, сопровождая их соответствующими расшифровками:

1. Основания имеют форму одинаковых многоугольников. В соответствии с форматом таких фигур определяют тип призмы. На рисунке выше представлен геометрический объект, обладающий основаниями в форме параллелограммов, а именно ABCD и \(A_{1}B_{1}C_{1}D_{1}1\).
2. Боковые грани в данном примере изображены как параллелограммы и обозначены за \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D и AA_{1}D_{1}1D\).
3. Боковое ребро является отрезком, с помощью которого соединены соответствующие друг другу вершины разных оснований \((AA_{1}, BB_{1}, CC_{1} и DD_{1})\). Боковое ребро играет роль единой стороны прилегания пары боковых граней.
4. Высота h представляет собой перпендикулярный отрезок прямой, обозначающий расстояние между парой оснований. Когда ребра по бокам призмы перпендикулярны рассматриваемым основаниям, считают, что такие ребра приобретают смысл высот геометрической фигуры.
5. Диагональ основания изображена в виде отрезка, соединяющего пару вершин, расположенных друг напротив друга на едином основании. На изображении диагонали обозначены отрезками \(AC, BD, A_{1}C_{1} и B_{1}D_{1}\). Если речь в задаче идет о треугольной призме, то диагональ отсутствует.
6. Диагональ боковой грани представляет собой отрезок, соединяющий пару вершин, которые расположены напротив друг друга и принадлежат одной грани. В геометрической фигуре, рассмотренной на графическом изображении, роль данных элементов играют отрезки \(CD_{1} и C_{1}D\).
7. Диагональ призмы является отрезком, с помощью которого соединены две вершины, принадлежащие неодинаковым основаниям и разным боковым граням. В качестве примера таких компонентов геометрического объекта можно привести фрагменты прямых \(AC_{1} и B_{1}D\).
8. Поверхность призмы является суммой поверхности пары оснований рассматриваемой фигуры и ее граней, расположенных по бокам.

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Решение.

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

V₁ = ha² = 10a²

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

V₂ = h (2a)² = 4ha²

Поскольку V₁ = V₂, можно приравнять выражения:

10a² = 4ha²

После сокращения обеих частей уравнения на a² получается:

10 = 4h

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.

ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Решение.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

Задание 3.

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Решение.

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.

Виды

Ранее была рассмотрена одна из самых простых разновидностей призмы. Существуют и другие конфигурации данного геометрического объекта. Ознакомимся с распространенными типами фигур, в основании которых треугольник. Начнем с прямой призмы. Таковой является объект с боковыми гранями, которые перпендикулярны относительно основания. Высота в прямой призме соответствует по величине ребру, расположенному сбоку. Ниже представлена типичная прямая призма.

 

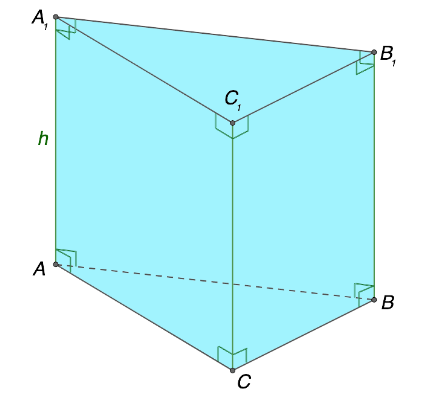
Выделяют в отдельную категорию следующую разновидность призмы, называемой наклонной. В отличие от предыдущего типа геометрического объекта здесь предусмотрено другое расположение боковых граней относительно оснований. Рассматриваемые отрезки не перпендикулярны относительно друг друга, а находятся под каким-либо углом.

 

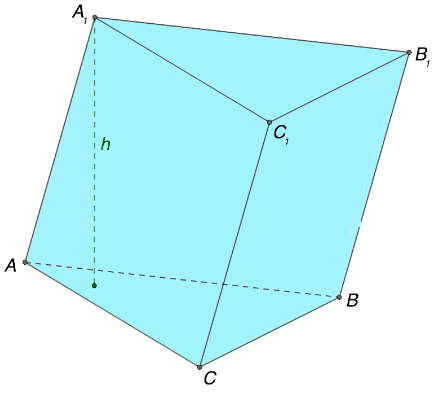
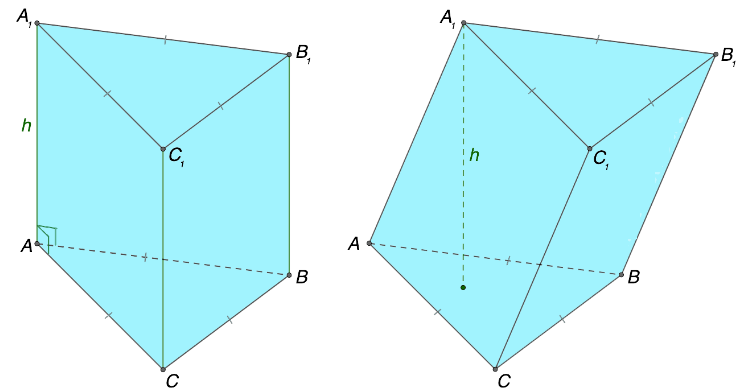
Как можно догадаться из названия, в основаниях правильной призмы расположены правильные многоугольники. В то же время этот геометрический объект способен обладать признаками прямой или наклонной фигуры. Представим на рисунке ниже описанную форму для наглядности:

 

Существует вид призмы, который получен путем некоторых действий. Так, например, при пересечении геометрического объекта какой-либо плоскостью, остается отдельный фрагмент, которому также свойственно определенная форма. Если используемая в процессе плоскость расположена не параллельно по отношению к основаниям призмы, то в результате получается ее часть, которую называют усеченной призмой. Как и в предыдущем примере, полученный путем несложных построений объект может быть отнесен к формату прямой или наклонной призмы. На рисунке для лучшего восприятия изображены оба варианта.

 

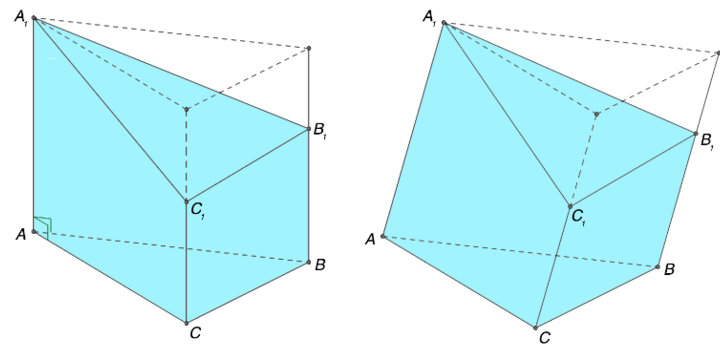
Примеры решения задач

Задача 1

Сторона, входящая в состав геометрической фигуры в виде правильной треугольной призмы, соответствует 6 см. Высота рассматриваемого объекта равна 8 см. Требуется вычислить значение полной площади поверхности призмы.

Решение

Начнем решение задания с анализа условий. Заметим, что при известных элементах геометрического объекта, можно воспользоваться формулой, в которой они учтены. Остается только подставить численные значения величин, исходя из данной информации, и вычислить искомую площадь:

\(S_{полн} = \frac{6\cdot 6 \cdot 8 + 6^{2}\cdot \sqrt{3}}{2}\approx 175,18\)

Ответ: \(175,18 см^{2}\).

Задача 2

Правильная шестиугольная призма обладает площадью полной поверхности, которая равна \(400 см^{2}\). Сторона основания этой геометрической фигуры составляет 5 см. На основе имеющихся данных требуется рассчитать значение высоты рассматриваемого объекта.

Решение

С формулой для определения площади полной поверхности уже довелось поработать в процессе поиска ответа к предыдущей задаче. Из этой математической закономерности несложно выразить высоту. Запишем соответствующее соотношение и путем подстановки численных значений найдем искомую величину:

\(h = \frac{S_{полн} — 3\sqrt{3}a^{2}}{6a} = \frac{400 — 3\cdot \sqrt{3}\cdot 5^{2}}{6\cdot 5} \approx 9\)

Ответ: 9 см.

Задача 3

Имеется некая геометрическая фигура, обладающая формой призмы. Площадь основания данного объекта составляет \(14 см^{2}\). При этом высота соответствует величине в 6 см. Необходимо вычислить объем призмы.

Решение

Процесс поиска ответа к этой задаче не вызывает сложностей, если вспомнить основную формулу для вычисления объема призмы. Остается лишь подставить известные по условию задания значения, выполнить простые алгебраические преобразования и записать итоговый результат:

\(V = 14 \cdot6 = 84\)

Ответ: \(84 см^{3}.\)

Задача 4

Объем геометрического объекта, представленного в виде призмы, соответствует \(106 см^{3}\). Площадь основания рассматриваемой фигуры равна \(10 см^{2}\). Нужно рассчитать величину, которой соответствует высота этой призмы.

Решение

В данном случае общая формула для расчета объема призмы также будет полезна. Нужно только выразить с помощью озвученной закономерности высоту:

\(h = \frac{V}{S_{осн}} = \frac{106}{10} = 10,6\)

Фигура призма

Перед тем как переходить к рассмотрению формул для площади основания и поверхности призмы того или иного вида, следует разобраться, о какой фигуре идет речь.

Призма в геометрии представляет собой пространственную фигуру, состоящую из двух параллельных многоугольников, которые равны между собой, и нескольких четырехугольников или параллелограммов. Количество последних всегда равно числу вершин одного многоугольника. Например, если фигура образована двумя параллельными n-угольниками, тогда количество параллелограммов будет равно n.

Соединяющие n-угольники параллелограммы называются боковыми сторонами призмы, а их суммарная площадь — это площадь боковой поверхности фигуры. Сами же n-угольники называются основаниями.

Выше рисунок демонстрирует пример призмы, изготовленной из бумаги. Желтый прямоугольник является ее верхним основанием. На втором таком же основании фигура стоит. Красный и зеленый прямоугольники — это боковые грани.

Призма

Определения:

1. Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
2. Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
3. Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
4. Боковая поверхность – объединение боковых граней.
5. Полная поверхность – объединение оснований и боковой поверхности.
6. Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
7. Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
8. Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
9. Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
10. Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
11. Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).
• Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
• Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁или BB₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

• Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
• Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны между собой.
4. Правильная призма является прямой.

Что такое призма

В жизни человека окружает множество геометрических фигур. Навыки определения их параметров являются полезными. В случае каждого объекта предусмотрены определенные правила и закономерности, которые значительно упрощают решение прикладных и теоретических задач. Одной из сложных и интересных фигур с точки зрения науки геометрии считают призму. Задания на вычисление сторон, площади, объема и прочих характеристик подобного объекта часто попадаются в контрольных и самостоятельных работах. Начнем с основного понятия этого геометрического объекта.

Призмой называют в геометрии пространственную фигуру в виде многогранника с парой параллельных и равных между собой граней, которые являются многоугольниками, и прочими гранями, имеющими форму параллелограммов.

Разобраться со сформулированным определением достаточно сложно. По этой причине целесообразно трансформировать определение в графический рисунок. На изображении, представленном ниже, расположена четырехугольная призма. По-другому этот объект принято именовать параллелепипедом.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

 

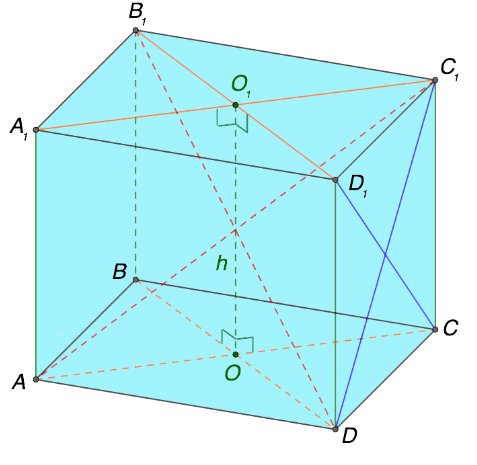
Расчет для косоугольной призмы

Определение значения площади боковой поверхности для данной фигуры выполнить несколько сложнее, чем для прямоугольной. Тем не менее приведенная выше формула остается той же самой, только вместо периметра основания следует взять периметр перпендикулярного среза, а вместо высоты — длину бокового ребра.

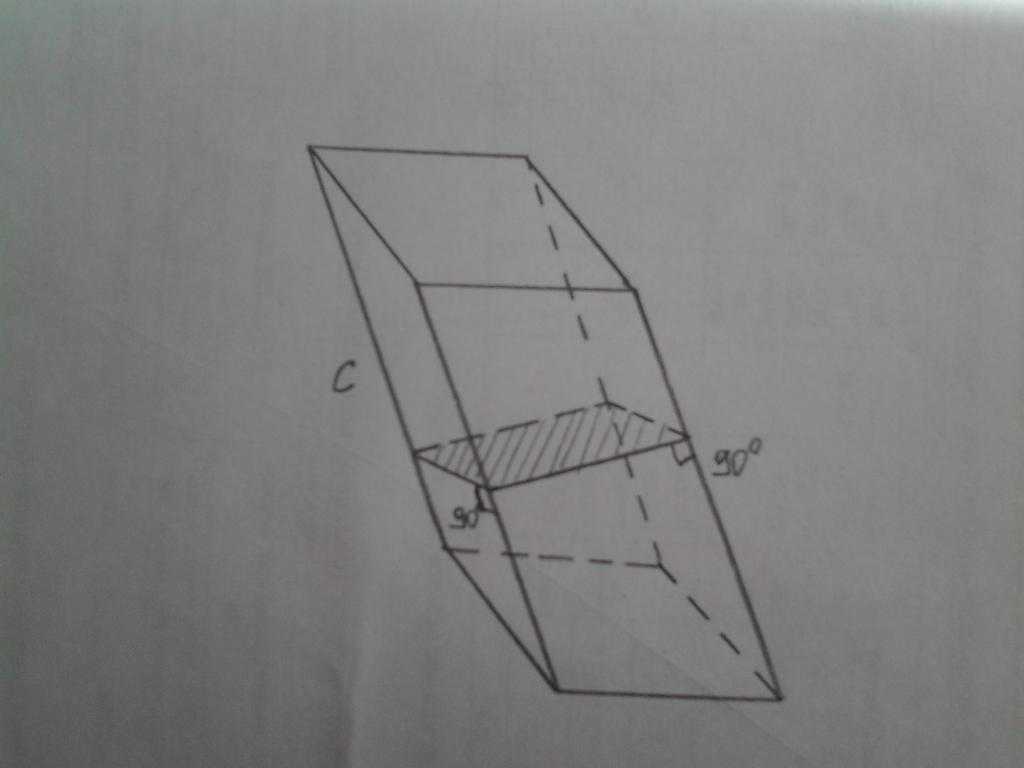
Рисунок выше демонстрирует четырехугольную косоугольную призму. Заштрихованный параллелограмм — это и есть тот перпендикулярный срез, периметр которого P sr необходимо рассчитать. Длина бокового ребра на рисунке обозначена буквой C. Тогда получаем формулу:

Периметр среза можно найти, если известны углы параллелограммов, образующих боковую поверхность.

Площадь основания призмы правильной

Пожалуй, самой простой задачей при работе с призмами является проблема нахождения площади основания правильной фигуры. Поскольку оно образовано n-угольником, у которого все углы и длины сторон являются одинаковыми, то всегда можно разделить его на одинаковые треугольники, у которых известны углы и стороны. Суммарная площадь треугольников будет площадью n-угольника.

Еще один способ определить часть площади поверхности призмы (основание) заключается в использовании известной формулы. Она имеет следующий вид:

То есть площадь S n n-угольника однозначно определяется исходя из знания длины его стороны a. Некоторую сложность при расчете по формуле может составить вычисление котангенса, особенно когда n>4 (для n≤4 значения котангенса — это табличные данные). Для определения этой тригонометрической функции рекомендуется воспользоваться калькулятором.

При постановке геометрической задачи следует быть внимательным, поскольку может потребоваться найти площадь оснований призмы. Тогда полученное по формуле значение следует умножить на два.

Боковая поверхность

Мы разобрали, как найти площадь основания призмы. Боковая поверхность этой фигуры всегда состоит из параллелограммов. Для прямых призм параллелограммы становятся прямоугольниками, поэтому суммарную их площадь вычислить легко:

Здесь b — длина бокового ребра, a i — длина стороны i-го прямоугольника, которая совпадает с длиной стороны n-угольника. В случае правильной n-угольной призмы получаем простое выражение:

Если призма является наклонной, тогда для определения площади ее боковой поверхности следует сделать перпендикулярный срез, рассчитать его периметр P sr и умножить его на длину бокового ребра.

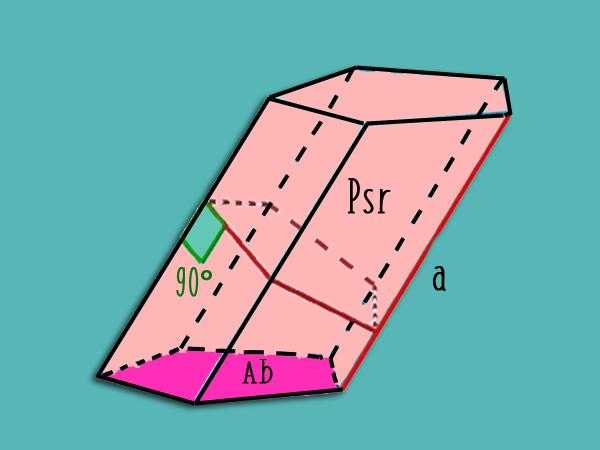
Рисунок выше показывает, как следует делать этот срез для наклонной пятиугольной призмы.

Это самые распространенные объемные фигуры среди остальных подобных, которые встречаются в быту и природе. Изучением их свойств занимается стереометрия, или пространственная геометрия. В данной статье раскроем вопрос о том, как можно найти площадь боковой поверхности правильной треугольной призмы, а также четырехугольной и шестиугольной.

Боковая поверхность призмы

Как было сказано в эта фигура состоит из n + 2 плоскостей, которые, пересекаясь, образуют n + 2 грани. Две из них принадлежат основаниям, остальные образованы параллелограммами. Площадь всей поверхности состоит из суммы площадей указанных граней. Если в нее не включать значения двух оснований, тогда мы получаем ответ на вопрос о том, как найти площадь боковой поверхности призмы. Так, можно определить ее значение и оснований отдельно друг от друга.

Ниже приводится для которой боковая поверхность образована тремя четырехугольниками.

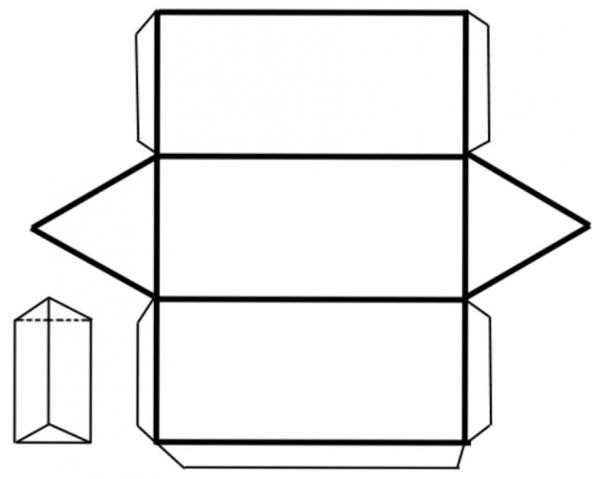
Рассмотрим процесс вычислений далее. Очевидно, что площадь боковой поверхности призмы равна сумме n площадей соответствующих параллелограммов. Здесь n — это число сторон многоугольника, образующего основание фигуры. Площадь каждого параллелограмма можно найти, если умножить длину его стороны на опущенную на нее высоту. Это касаемо общего случая.

Если изучаемая призма является прямой, тогда процедура определения площади ее боковой поверхности S b значительно облегчается, поскольку такая поверхность состоит из прямоугольников. В этом случае можно воспользоваться следующей формулой:

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади боковой поверхности и двух площадей основания.

Полный = Страница. + 2Сбас.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.

Страница = Поз. ⋅ ч

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

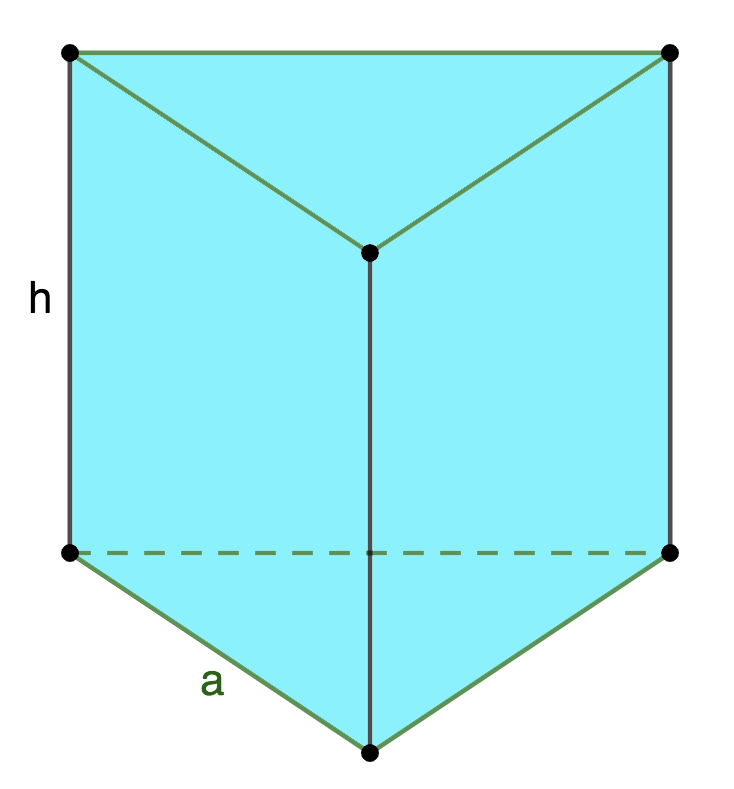
Основание: равносторонний треугольник.

Квадрат	Формула
база
боковая поверхность	Страница = 3ah» data-order=»Sбок. = 3ah»>Страница = 3ah
полный

3. Площадь правильной четырехугольной призмы

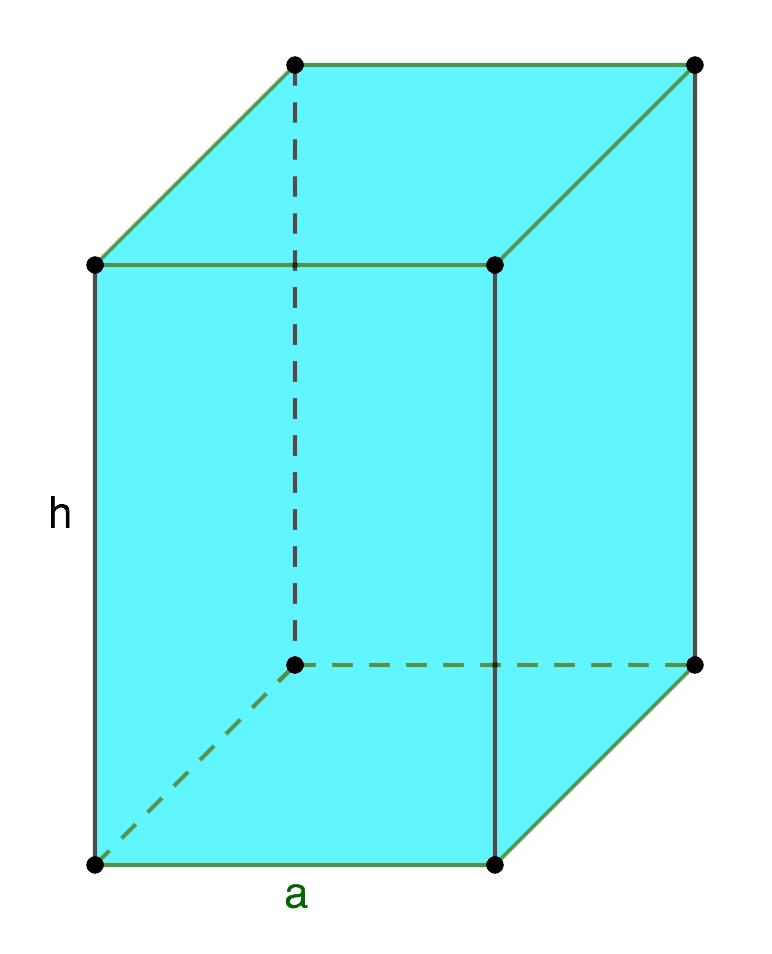
Основание: квадрат.

Квадрат	Формула
база	Сосн. = a2″заказ данных=»Sосн. = a2″>Sбаза = а2
боковая поверхность	Страница = 4ah» data-order=»Sбок. = 4ah»> Страница = 4ah
полный	Полный = 2a2 + 4ah» data-order=»Sполн. = 2a2 + 4ah»>Полный = 2a2 + 4ah

Примечание: если высота правильной квадратной призмы равна длине стороны основания, то мы имеем дело с кубом, площадь катета которого равна а2. А так как все шесть граней куба равны, то общая площадь грани равна 6а2.

4. Площадь правильной шестиугольной призмы

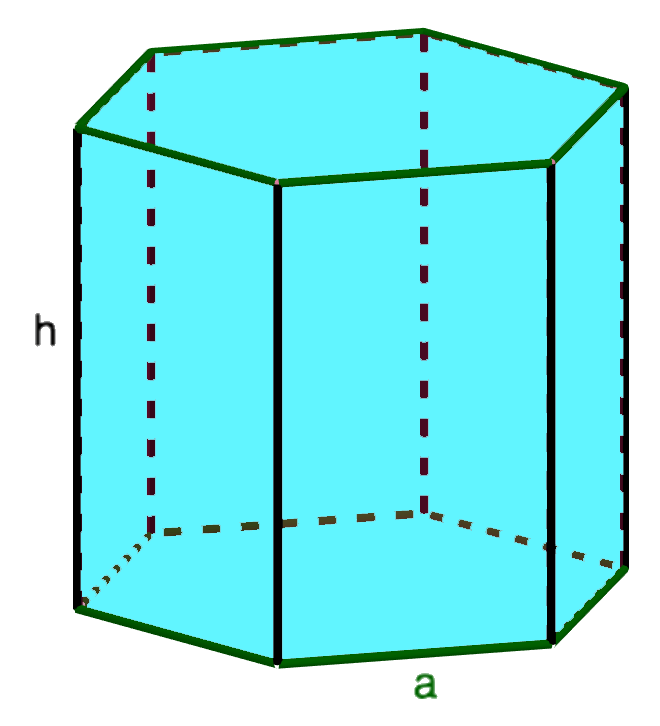
Основание: правильный шестиугольник

Квадрат	Формула
база
боковая поверхность	Страница = 6ah» data-order=»Sбок. = 6ah»>Страница = 6ah
полный