Что такое правильный многоугольник

В природе

Дорога гигантов в Северной Ирландии

Многоугольники появляются в горных породах, чаще всего в виде плоских граней кристаллов , где углы между сторонами зависят от типа минерала, из которого сделан кристалл.

Правильные шестиугольники могут возникать, когда при охлаждении лавы образуются области плотно упакованных столбов базальта , которые можно увидеть на Дороге гигантов в Северной Ирландии или в Дьявольской столбе в Калифорнии .

В биологии поверхность восковых сот, созданных пчелами, представляет собой массив шестиугольников , а стороны и основание каждой соты также представляют собой многоугольники.

Формула для нахождения внутреннего угла правильного многоугольника

Внутренний угол правильного многоугольника — это угол, образованный двумя сторонами многоугольника, измеряемый внутрь многоугольника.

Для нахождения внутреннего угла правильного многоугольника с n сторонами (n-угольника) существует следующая формула:

Внутренний угол = (n-2) * 180 / n

В этой формуле n — количество сторон многоугольника.

Например, для треугольника (3-угольника) существует формула:

Внутренний угол = (3-2) * 180 / 3 = 60 градусов

Для четырехугольника (квадрата) существует формула:

Внутренний угол = (4-2) * 180 / 4 = 90 градусов

И так далее для любого правильного многоугольника.

Эта формула позволяет легко находить величину внутреннего угла правильного многоугольника без необходимости измерять его с помощью угломера или других инструментов.

Площадь выпуклых многоугольников

Нередко при решении различных задач элементарной геометрии появляется необходимость определить площадь выпуклого многоугольника. Предположим, что (Xi. Yi), i = 1,2,3… n представляет собой последовательность координат всех соседних вершин многоугольника, не имеющего самопересечений. В этом случае его площадь вычисляется по такой формуле:

S = ½ (∑ (X i + X i + 1) (Y i + Y i + 1)),

где (Х 1 , Y 1) = (X n +1 , Y n + 1).

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию

Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

На этом уроке мы приступим уже к новой теме и введем новое для нас понятие «многоугольник». Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.

Тема: Четырехугольники

Урок: Многоугольники

Обобщение

Идея многоугольника были обобщены различными способами. Некоторые из наиболее важных включают:

• A сферический многоугольник — это цепь дуг больших окружностей (сторон) и вершин на поверхности сферы. Он позволяет использовать digon, многоугольник, имеющий только две стороны и два угла, что невозможно на плоской плоскости. Сферические многоугольники играют важную роль в картографии (создание карт), а в конструкции Витоффа из однородных многогранников.
• A косой многоугольник не лежит на плоской плоскости., но зигзагами в трех (или более) измерениях. Многоугольники Петри правильных многогранников — хорошо известные примеры.
• Апейрогон — это бесконечная последовательность сторон и углов, которая не замкнута, но не имеет концов, потому что он неограниченно простирается в обоих направлениях.
• A наклонный апейрогон представляет собой бесконечную последовательность сторон и углов, которые не лежат в плоскости.
• A сложный многоугольник представляет собой конфигурацию аналогичную в обычный многоугольник, который существует в комплексной плоскости двух реальных и двух мнимых измерений.
• абстрактный многоугольник — алгебраический частично упорядоченный набор, представляющий различные элементы (стороны, вершины и т. Д.) И их связь. Реальный геометрический многоугольник называется реализацией связанного абстрактного многоугольника. В зависимости от отображения могут быть реализованы все описанные здесь обобщения.
• A Многогранник — трехмерное твердое тело, ограниченное плоскими многоугольными гранями, аналогично многоугольнику в двух измерениях. Соответствующие формы в четырех или более высоких измерениях называются многогранниками. (В других соглашениях слова многогранник и многогранник используются в любом измерении, с той разницей, что многогранник обязательно ограничен.)

Доказательства свойств углов многоугольника

Теорема 1. В любом треугольнике сумма углов равна 180°.

Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).

Рис.3

Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.

Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).

Рис.4

Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.

Замечание. Теорема 1 является следствием теоремы 2.

Теорема 3. Сумма углов  – угольникаn равна

Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).

Рис.5

Получим n треугольников:

OA1A2,  OA2A3,  …  OAnA1

Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна

что и требовалось доказать.

Теорема 4. Сумма внешних углов  – угольникаn , взятых по одному у каждой вершины, равна 360°.

Доказательство. Рассмотрим рисунок 6.

Рис.6

В соответствии рисунком 6 справедливы равенства

Теорема доказана.

Удвоение числа сторон правильного описанного многоугольника

Чтобы удвоить число сторон правильного описанного многоугольника нужно разделить дуги ab, bc, cd, … пополам и провести через точки деления отрезки mn, pg, rs, … до пересечения их со сторонами данного многоугольника (черт. 199).

В этом случае образуется многоугольник равноугольный, ибо его углы измеряются одинаковой мерой. В равноугольном же описанном многоугольнике стороны равны (теорема 120).

Периметр описанного многоугольника с удвоенным числом сторон уменьшается.

Действительно,

An > αn
Bp > βp, следовательно,
AB > αn + np + pβ

Такие же равенства имеют место и для сторон BC, CD, … и т. д. Сложив их, находим, что

AB + BC + CD + … > mn + np + pq + …
или P_n > P_2n

где P_n и P_2n означают периметры правильных описанных многоугольников, имеющих n и 2n сторон.

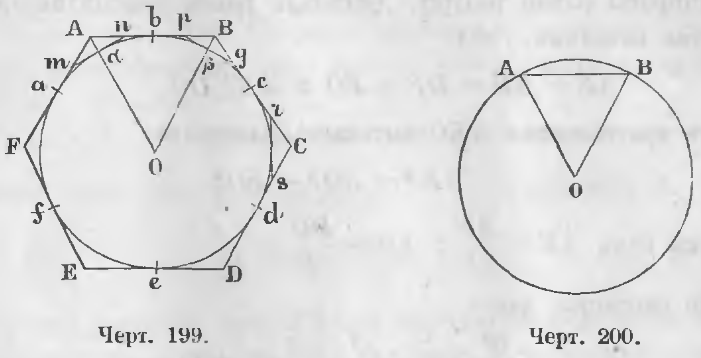
Теорема 125. Сторона правильного вписанного шестиугольника равна радиусу (a₆ = r).

Дано. Пусть AB сторона правильного шестиугольника (черт. 200), вписанного в круг, радиус которого обозначим через r.

Требуется доказать, что AB = a₆ = r.

Доказательство. Дуга AB равна 60°. Соединив A и B с центром O, имеем треугольник ABO, у которого угол AOB имеет 60° = (2/3)d.

Углы A и B равны, следовательно, из равенства A + B + O = 2d, имеем:

2A + (2/3)d = 2d, откуда A = B = (2/3)d

Таким образом треугольник ABO равносторонний и следовательно AB = AO = r.

Теорема 126. Сторона правильного вписанного треугольника равна радиусу, умноженному на √3 (a₃ = r√3).

Дан правильный вписанный треугольник ABC (черт. 201).

Требуется доказать, что AB = r√3.

AE = EB = DE = EO и AB ⊥ DO.

Из треугольника AEO вытекает равенство

AE2 = AO2 — EO2

Так как AE = AB/2, EO = DO/2 = r/2, то это равенство дает

AB2/4 = r2 — r2/4 = (3/4)r2, откуда
AB = a₃ = r√3 (ЧТД).

Теорема 127. Сторона вписанного квадрата равна радиусу, умноженному на √2.

Дан правильный вписанный четырехугольник или квадрат ABCD (черт. 202).

Требуется доказать, что AB = r√2.

Доказательство. Соединим B с D. Отрезок BD есть диаметр, ибо прямой угол B опирается на концы диаметра.

Из прямоугольного треугольника ABD вытекает равенство

AB2 + AD2 = BD2

Так как AB = AD, BD = 2r, то

2AB2 = 4r2, откуда AB = a₄ = r√2 (ЧТД).

Теорема 128. Сторона правильного вписанного десятиугольника равна большей части радиуса, разделенного в крайнем и среднем отношении.

Дано. Положим AB есть сторона правильного вписанного десятиугольника (черт. 203), следовательно, дуга AB = 1/10 окружности и

∠AOB = (4d)/10 = (2/5)d.

Требуется доказать, что AB есть большая часть радиуса среднепропорциональная между целым радиусом и меньшей его частью.

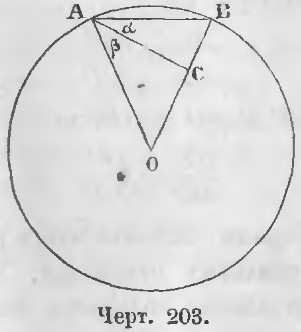
Доказательство. Соединим точки A и B с центром и разделим угол BAO пополам.

∠AOB = (2/5)d

В равенстве ∠BAO + ∠ABO + ∠AOB = 2d

∠BAO = ∠ABO, следовательно, ∠BAO = ∠ABO = (4/5)d.

Так как ∠α = ∠β по построению, то из равенства

∠α + ∠β = (4/5)d следует, что ∠α = ∠β = (2/5)d

Треугольник ABC равнобедренный, ибо

∠α = (2/5)d, ∠B = (4/5)d,

следовательно, из равенства

∠α + ∠B + ∠ACB = 2d имеем:
(2/5)d + (4/5)d + ∠ACB = 2d и ∠ACB = (4/5)d.

Таким образом

∠ACB = ∠ABC = (4/5)d

следовательно,

AB = AC

Треугольник ACO тоже равнобедренный, ибо

∠β = (2/5)d и ∠AOB = (2/5)d

следовательно, AC = CO и таким образом AB = AC = CO.

Так как отрезок AC делит угол треугольника пополам, то имеет место пропорция (теорема 98)

AO/AB = OC/CB

Так как AB = OC и AO = OB, то

OB/OC = OC/CB

откуда видно, что OC равно большей части радиуса OB, разделенного в крайнем и среднем отношении. Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.

Обозначив ее через a₁₀, а радиус через r, имеем пропорцию

r/a₁₀ = a₁₀/(r — a₁₀)

откуда положительное решение квадратного уравнения, определяющее сторону правильного вписанного десятиугольника, будет:

a₁₀ = ((√5 — 1)/2)r.

Формула угла правильного многоугольника

Существует закономерность, согласно которой можно рассчитать угол правильного многоугольника. Известно, что для любого выпуклого n-угольника сумма углов составляет \(180^{0}(n-2)\). Предположим, что угол правильного многоугольника обозначен \alpha. Исходя из того, что у такой геометрической фигуры n углов, и они равны, можно записать следующее равенство:

\(n*\alpha =180^{0}(n-2)\)

Из записанного выражения можно выразить \(\alpha\), то есть записать формулу угла правильного многоугольника:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

В данном случае n обозначает число сторон многоугольника.

Справедливость записанной формулы можно проверить на примере равностороннего треугольника и квадрата. В случае треугольника n=3, а угол составляет \(60^{0}\). Его можно определить по формуле:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(3-2)}{3}=\frac{180^{0}*1}{3}=60^{0}\)

В случае квадрата, у которого n=4, угол равен \(90^{0}\), что легко рассчитать:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(4-2)}{4}=\frac{180^{0}*2}{4}=90^{0}\)

Используя данную закономерность можно определить углы других правильных многоугольников.

Угол правильного пятиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(5-2)}{5}=\frac{180^{0}*3}{5}=108^{0}\)

Угол правильного шестиугольника составляет:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(6-2)}{6}=\frac{180^{0}*4}{6}=120^{0}\)

Угол правильного восьмиугольника равен:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(8-2)}{8}=\frac{180^{0}*6}{8}=135^{0}\)

В случае правильного многоугольника с 50 углами, каждый угол составит:

\(\alpha =\frac{180^{0}(n-2)}{n}=\frac{180^{0}(50-2)}{50}=\frac{180^{0}*48}{50}=172,8^{0}\)

Далее в качестве примера использования формулы угла правильного n-угольника можно рассмотреть задачу на определение числа сторон у правильного многоугольника, каждый угол которого составляет \(179^{0}.\)

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(179=\frac{180(n-2)}{n}\)

\(179n=180(n-2)\)

\(179n=180n-360\)

\(179n-180n=-360\)

\(-n=-360\)

\(n=360\)

Таким образом, рассматриваемый правильный многоугольник обладает 360 сторонами.

С помощью формулы угла правильного многоугольника можно определить, существует ли такой правильный многоугольник, угол которого составляет \(145^{0}\). В том случае, когда такая геометрическая фигура существует, формула примет вид:

\(\alpha =\frac{180^{0}(n-2)}{n}\)

\(145=\frac{180(n-2)}{n}\)

\(145n=180(n-2)\)

\(145n=180n-360\)

\(145n-180n=-360\)

\(-35n=-360\)

\(n=\frac{360}{35}=\frac{72}{7}=10\frac{2}{7}\)

Как найти периметр многоугольника и определить диагонали

Периметром многоугольника называется сумма длин его сторон.

Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.

Пример

Задание: Длина одной стороны четырехугольника ABCD равна 3 см. Требуется найти
периметр четырехугольника.

Решение: AB + BC + CD + DA = 3 + 3 + 3 + 3 = 12 см

Ответ: периметр четырехугольника ABCD равен 12 см.

Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.

Например, отрезок AD будет являться диагональю фигуры ABCDEF:

Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.

Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:

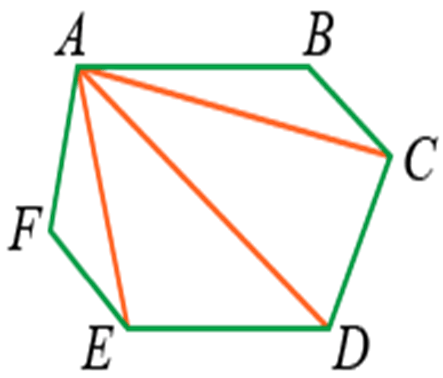
Количество треугольников будет на 2 меньше, чем число сторон:

Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.

Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.

Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

• вершин;
• сторон;
• углов.

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n-угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

Понятие правильного многоугольника

У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.

Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.

Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник

Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными

Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:

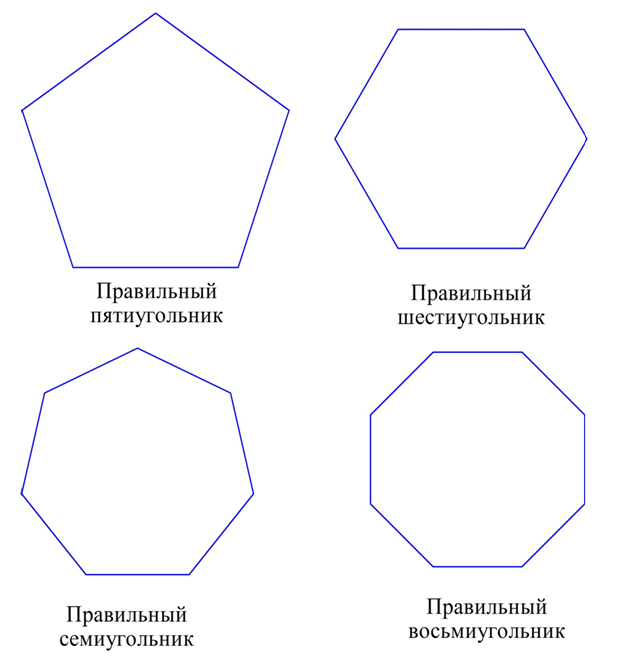
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:

Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:

Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?

Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:

Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?

Решение. В формулу 

Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?

Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:

Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.

Ответ: не может.

Виды геометрических фигур

Множество точек дает линию, а из нескольких соединенных между собой линий можно получить различные геометрические фигуры на плоскости и в пространстве. Таким образом, произвольное множество точек позволяет нам создавать геометрическую фигуру. Это может быть квадрат или куб, круг или шар, а также более сложные и неоднозначные фигуры, например икосаэдр, который может быть представлен двумя разными формами.

«Бери и Делай» предлагает узнать, чем отличаются разные виды геометрических фигур.

Плоские геометрические фигуры

Плоская геометрическая фигура располагается в двумерном пространстве, где объекты характеризуются только длиной и шириной. Различают следующие фигуры:

• Круг — это фигура, у которой нет углов и в которой все точки по окружности находятся на равном расстоянии от центра.
• Овал — это фигура, похожая на яйцо. У нее также нет углов.
• Квадрат — это фигура, у которой 4 равные стороны и 4 прямых угла.
• Прямоугольник — это фигура, похожая на квадрат: у нее 4 стороны и они пересекаются под прямым углом. В отличие от квадрата, у прямоугольника только противолежащие стороны равны. Если с помощью отрезка соединить любой угол с противоположным, получится диагональ. И у квадрата, и у прямоугольника диагонали равны.
• Ромб — это фигура, у которой 4 равные стороны, но пересекаются они не под прямыми углами. У ромба противоположные углы ромба равны. Ромб, так же как квадрат и прямоугольник, является четырехугольником.
• Треугольник — это фигура, у которой 3 угла и 3 стороны. Точки, в которых пересекаются стороны треугольника, принято называть его вершинами.

Виды треугольников в зависимости от размера углов:

остроугольный — все углы острые (каждый равен менее 90°)

тупоугольный — один угол является тупым (равным более 90°)

прямоугольный — один угол является прямым (равным 90°)

Различают также виды треугольников по соотношению их сторон:

равносторонний имеет 3 равные стороны

равнобедренный — 2 равные стороны

разносторонний — 3 разные стороны

Выше мы рассмотрели основные геометрические фигуры на плоскости. Но существует множество других, например:

• Трапеция — это четырехугольник, у которого как минимум 2 стороны параллельны. Таким образом, квадрат, ромб и прямоугольник можно рассматривать как частные случаи трапеции.
• Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. Так, прямоугольник, квадрат и ромб считаются частными случаями параллелограмма.
• Пентагон — фигура, представляющая собой правильный многоугольник с 5 сторонами. У пентагона все стороны и углы равны.
• Гексагон — это правильный многоугольник, у которого 6 равных сторон, а углы образуют 6 равносторонних треугольников.
• Крест — это фигура, которая состоит из 2 пересекающихся линий или прямоугольников.
• Звезда — плоский невыпуклый многоугольник, по форме напоминающий звезду. Звезда может быть трехконечной, четырехконечной, пятиконечной (как на картинке выше) и так далее.

Геометрическая фигура может быть выпуклой, если ей целиком принадлежат все точки отрезка, соединяющего любые ее две точки. Круг, шар, овал и треугольник являются выпуклыми фигурами. А четырехугольники могут быть как выпуклыми, так и невыпуклыми. К примеру, на картинке выше изображена одна и та же фигура — дельтоид. Это четырехугольник, стороны которого можно сгруппировать в две пары равных смежных сторон. Слева — дельтоид выпуклый, а справа — невыпуклый.

Пространственные геометрические фигуры

Если фигура располагается в трехмерном пространстве, где объекты характеризуются длиной, шириной и высотой, а также имеют глубину или толщину, ее называют пространственной. Чаще всего различают следующие пространственные фигуры: