Примеры задач с решениями
Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.
Задание 1.
В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?
Решение.
Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:
V₁ = ha² = 10a²
Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:
V₂ = h (2a)² = 4ha²
Поскольку V₁ = V₂, можно приравнять выражения:
10a² = 4ha²
После сокращения обеих частей уравнения на a² получается:
10 = 4h
В результате новый уровень песка составит h = 10 / 4 = 2,5 см.
Задание 2.
ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.
Решение.
Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.
Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.
Длина любого ребра определяется через известную диагональ:
a = d / √2 = 6√2 / √2 = 6
Площадь полной поверхности находится по формуле для куба:
Sполн = 6a² = 6·6² = 216
Задание 3.
В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?
Решение.
Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.
Длина комнаты составляет a = √9 = 3 м.
Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².
Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.
Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.
Основные определения и свойства призм. Теорема Эйлера
Определение 1. Рассмотрим две α и β , , и произвольный выпуклый A1A2 … An , лежащий в плоскости α (рис. 1).
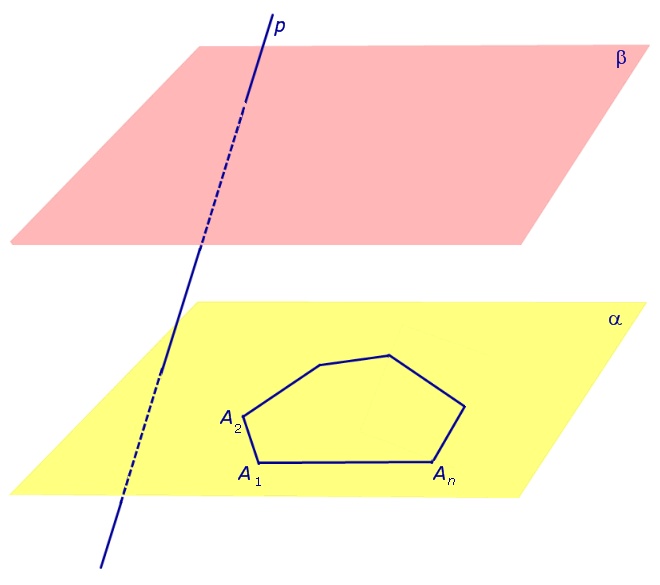
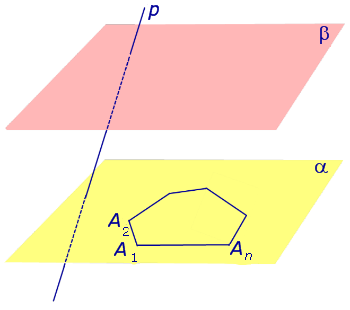
Рис.1
Если через каждую точку многоугольника A1A2 … An провести прямую, p , и обозначить символами A’1, A’2, … , A’n точки пересечения с плоскостью β прямых, p и проходящих через точки A1, A2, … , An, то полученную фигуру A1A2 … An A’1A’2 … A’n называют n – угольной призмой (рис.2).
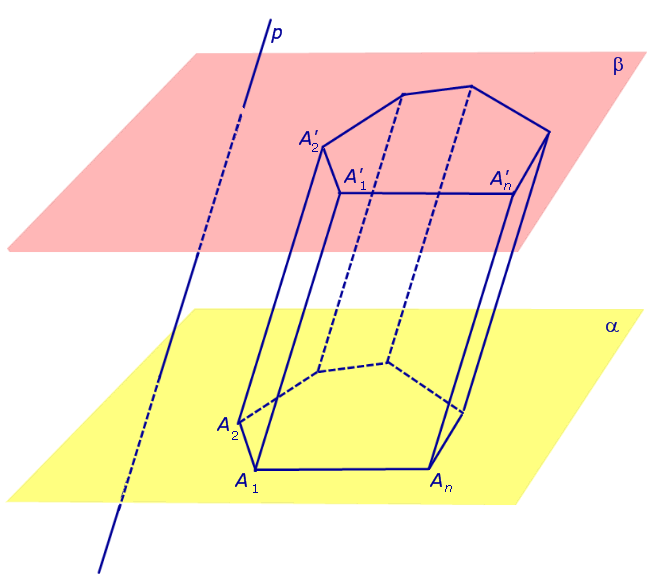
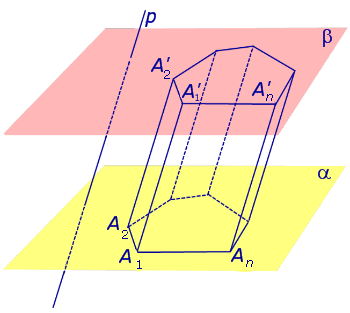
Рис.2
Утверждение 1. Каждый из n четырехугольников
A1A2A’2A’1, A2A3A’3A’2, … , AnA1A’1A’n
является .
Доказательство. Докажем сначала, что параллелограммом является, например, четырехугольник A1A2A’2A’1. Для этого заметим, что стороны A1A’1 и A2A’2 параллельны по построению. Заметим также,что прямая A1A2 β , так как лежит в плоскости α , которая β . Прямая A’1A’2 является линией пересечения плоскости A1A2A’2A’1 с плоскостью β . Из следует, что прямая A’1A’2 параллельна прямой A1A2 . Таким образом, у четырехугольника A1A2A’2A’1 противоположные стороны попарно параллельны, то есть A1A2A’2A’1 – .
Для остальных четырехугольников доказательство проводится аналогично.
Определение 2.
A1A2A’2A’1, A2A3A’3A’2, … , AnA1A’1A’n
называют боковыми гранями призмы. Совокупность всех боковых граней призмы составляет боковую поверхность призмы.
Определение 3. A1A2 … An и A’1A’2 … A’n называют основаниями призмы.
Определение 4. Точки A1, A2, … , An , A’1, A’2, … , A’n ( A1A2 … An и A’1A’2 … A’n ) называют вершинами призмы.
Определение 5. Отрезки A1A’1 , A2A’2 , … , AnA’n называют боковыми ребрами призмы.
Утверждение 2 . Все боковые ребра призмы равны.
Это утверждение непосредственно вытекает из .
Определение 6. Отрезки A1A2 , A2A3 , … , AnA1 , … , A’1A’2 , A’2A’3 , … , A’nA’1 ( A1A2 … An и A’1A’2 … A’n ) называют ребрами оснований призмы.
Замечание 1. В случае, когда не требуется делать специальных уточнений,
|
боковые ребра и ребра оснований называют ребрами призмы, |
|
|
боковые грани и основания призмы называют гранями призмы |
|
|
совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы, |
|
|
n – угольные призмы называют призмами. |
Теорема Эйлера . Для любой призмы справедливо равенство:
|
+ |
|
– |
|
= | 2 |
|
+ |
|
– |
|
= | 2 |
|
+ |
|
– |
| – |
|
= | 2 |
Доказательство. Заметим, что у n – угольной призмы 2n вершин, n боковых граней, 2 основания, 2n ребер основания и n боковых ребер. Следовательно, у n – угольной призмы (n + 2) грани и 3n ребер.
Поскольку
2n + (n + 2) – 3n = 2
то теорема Эйлера доказана.
Определение 7., на которых лежат основания призмы, называют высотой призмы.
Замечание 2. С различными формулами для вычисления объема призмы и площадей можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».
Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
Примеры призм. Треугольные призмы. Четырехугольные призмы.Параллелепипеды
| Призма | Рисунок | Свойства |
| Наклонная треугольная призма |
AA1, BB1, CC1 не ABС и A1B1C1. ABС – произвольный треугольник. |
|
| Прямая треугольная призма |
AA1, BB1, CC1 ABС и A1B1C1. ABС – произвольный треугольник. прямой треугольной призмы – . равна длине . |
|
| Правильная треугольная призма |
AA1, BB1, CC1 ABС и A1B1C1. ABС – . правильной треугольной призмы – . равна длине . |
|
| Наклонная четырехугольная призма |
AA1, BB1, CC1,DD1 не ABСD и A1B1C1D1. ABСD – произвольный четырехугольник. |
|
| Прямая четырехугольная призма |
AA1, BB1, CC1, DD1 ABСD и A1B1C1D1. ABСD – произвольный четырехугольник. прямой четырехугольной призмы – . равна длине . |
|
| Правильная четырехугольная призма |
AA1, BB1, CC1, DD1 ABСD и A1B1C1D1. ABСD – . правильной четырехугольной призмы – . равна длине . |
|
| Параллелепипед |
все которой . Противоположные параллелепипеда равны. |
|
| Прямой параллелепипед |  |
, ABСD и A1B1C1D1 которой – . равна длине . |
| Прямоугольный параллелепипед |
, ABСD и A1B1C1D1 которой – . Все прямоугольного параллелепипеда являются . |
|
| Правильный параллелепипед |
Синоним термина ABСD и A1B1C1D1 – равные , – равные . равна длине . |
|
| Куб |
Правильный параллелепипед, у которого все равные . У куба все равны и попарно перпендикулярны. равна длине . |
| Наклонная треугольная призма |
|
Свойства: AA1, BB1, CC1 не ABС и A1B1C1.ABС – произвольный треугольник. |
| Прямая треугольная призма |
|
Свойства: AA1, BB1, CC1 ABС и A1B1C1.ABС – произвольный треугольник. прямой треугольной призмы – . равна длине . |
| Правильная треугольная призма |
|
Свойства: AA1, BB1, CC1 ABС и A1B1C1.ABС – . правильной треугольной призмы – . равна длине . |
| Наклонная четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 не ABСD и A1B1C1D1.ABСD – произвольный четырехугольник. |
| Прямая четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 ABСD и A1B1C1D1.ABСD – произвольный четырехугольник. прямой четырехугольной призмы – . равна длине . |
| Правильная четырехугольная призма |
|
Свойства: AA1, BB1, CC1, DD1 ABСD и A1B1C1D1.ABСD – . правильной четырехугольной призмы – . равна длине . |
| Параллелепипед |
|
Свойства:все которой .Противоположные параллелепипеда равны. |
| Прямой параллелепипед |
|
Свойства:, ABСD и A1B1C1D1 которой – . равна длине . |
| Прямоугольный параллелепипед |
|
Свойства:, ABСD и A1B1C1D1 которой – .Все прямоугольного параллелепипеда являются . |
| Правильный параллелепипед |
|
Свойства:Синоним термина ABСD и A1B1C1D1 – равные , – равные . равна длине . |
| Куб |
|
Свойства:Правильный параллелепипед, у которого все равные .У куба все равны и попарно перпендикулярны. равна длине . |
Примеры решения задач
Задача 1
Сторона, входящая в состав геометрической фигуры в виде правильной треугольной призмы, соответствует 6 см. Высота рассматриваемого объекта равна 8 см. Требуется вычислить значение полной площади поверхности призмы.
Решение
Начнем решение задания с анализа условий. Заметим, что при известных элементах геометрического объекта, можно воспользоваться формулой, в которой они учтены. Остается только подставить численные значения величин, исходя из данной информации, и вычислить искомую площадь:
\(S_{полн} = \frac{6\cdot 6 \cdot 8 + 6^{2}\cdot \sqrt{3}}{2}\approx 175,18\)
Ответ: \(175,18 см^{2}\).
Задача 2
Правильная шестиугольная призма обладает площадью полной поверхности, которая равна \(400 см^{2}\). Сторона основания этой геометрической фигуры составляет 5 см. На основе имеющихся данных требуется рассчитать значение высоты рассматриваемого объекта.
Решение
С формулой для определения площади полной поверхности уже довелось поработать в процессе поиска ответа к предыдущей задаче. Из этой математической закономерности несложно выразить высоту. Запишем соответствующее соотношение и путем подстановки численных значений найдем искомую величину:
\(h = \frac{S_{полн} — 3\sqrt{3}a^{2}}{6a} = \frac{400 — 3\cdot \sqrt{3}\cdot 5^{2}}{6\cdot 5} \approx 9\)
Ответ: 9 см.
Задача 3
Имеется некая геометрическая фигура, обладающая формой призмы. Площадь основания данного объекта составляет \(14 см^{2}\). При этом высота соответствует величине в 6 см. Необходимо вычислить объем призмы.
Решение
Процесс поиска ответа к этой задаче не вызывает сложностей, если вспомнить основную формулу для вычисления объема призмы. Остается лишь подставить известные по условию задания значения, выполнить простые алгебраические преобразования и записать итоговый результат:
\(V = 14 \cdot6 = 84\)
Ответ: \(84 см^{3}.\)
Задача 4
Объем геометрического объекта, представленного в виде призмы, соответствует \(106 см^{3}\). Площадь основания рассматриваемой фигуры равна \(10 см^{2}\). Нужно рассчитать величину, которой соответствует высота этой призмы.
Решение
В данном случае общая формула для расчета объема призмы также будет полезна. Нужно только выразить с помощью озвученной закономерности высоту:
\(h = \frac{V}{S_{осн}} = \frac{106}{10} = 10,6\)
Как выглядит призма
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:
- Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
- Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
- Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
- Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).
Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.
Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).
Вместо заключения
Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:
- Физика– устройство для преломления световых лучей.
- Риторика– оценка с учетом определенных факторов. Например, «Он смотрел на нее через призму прожитых лет» или «Он общался с ними через призму своего настроения».
- Техника– элемент металлорежущего станка, который предназначен для закрепления на нем цилиндрической заготовки.
А еще «Призма» — это кодовое название советской радиостанции 5-АК. Есть такой хоккейный клуб в Латвии – «Призма-Рига». И наконец, в Финляндии существует сеть продуктовых магазинов «PRISMA».
Вычисление объема
Рассмотрим произвольную призму из числа прямых, правильных или наклонных. Представим изображение на рисунке и обозначим все компоненты такого геометрического объекта.
Вычислить, чему равен объем такой призмы, можно с помощью следующей формулы:
\(V = S_{осн} \cdot h\)
Таким образом, для определения объема геометрического объекта, обладающего всеми признаками любой из перечисленных выше разновидностей призмы, следует найти результат от умножения площади основания и высоты фигуры. С целью расчета первого параметра необходимо рассмотреть многоугольник с четырьмя углами, который обозначен на рисунке за ABCD или EFGH.
Призма
Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.
- Боковое ребро – отрезок, соединяющий соответствующие друг другу вершины разных оснований (AA1, BB1, CC1 и DD1). Является общей стороной двух боковых граней.
- Высота (h) – это перпендикуляр, проведенный от одного основания к другому, т.е. расстояние между ними. Если боковые ребра расположены под прямым углом к основаниям фигуры, значит они одновременно являются и высотами призмы.
- Диагональ основания – отрезок, который соединяет две противолежащие вершины одного и того же основания (AC, BD, A1C1 и B1D1). У треугольной призмы данного элемента нет.
- Диагональ боковой грани – отрезок, который соединяет две противолежащие вершины одной и той же грани. На рисунке изображены диагонали только одной грани (CD1 и C1D), чтобы не перегружать его.
- Диагональ призмы – отрезок, соединяющий две вершины разных оснований, не принадлежащих одной боковой грани. Мы показали только две из четырех: AC1 и B1D.
- Поверхность призмы – суммарная поверхность двух ее оснований и боковых граней.
Основные свойства призмы
- Основы призмы — равные многоугольники.
- Боковые грани призмы — параллелограммы.
- Боковые ребра призмы параллельны и равны между собой.
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
- Высота прямой призмы равна длине бокового ребра.
- Высота наклонной призмы всегда меньше длины ребра.
- В прямой призме гранями могут быть прямоугольниками или квадратами.
Варианты сечения призмы
1. Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.
Примечание: у треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
2. Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.
Виды призм
Рассмотрим разновидности фигуры с треугольным основанием.
- Прямая призма– это такая геометрическая фигура, у которой боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
- Наклонная призма– боковые грани фигуры не перпендикулярны ее основаниям.
- Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
- Усеченная призма– часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.
Призма
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.
Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:
где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:
где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).
Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:
где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):
где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:
Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Элементы
Перед тем, как приступить к разбору и решению геометрических задач, следует разобраться с терминологией. Введем понятия для всех основных компонентов призмы. Сделать это целесообразно, используя рисунок, представленный ниже:
Перечислим элементы геометрического объекта, сопровождая их соответствующими расшифровками:
- Основания имеют форму одинаковых многоугольников. В соответствии с форматом таких фигур определяют тип призмы. На рисунке выше представлен геометрический объект, обладающий основаниями в форме параллелограммов, а именно ABCD и \(A_{1}B_{1}C_{1}D_{1}1\).
- Боковые грани в данном примере изображены как параллелограммы и обозначены за \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D и AA_{1}D_{1}1D\).
- Боковое ребро является отрезком, с помощью которого соединены соответствующие друг другу вершины разных оснований \((AA_{1}, BB_{1}, CC_{1} и DD_{1})\). Боковое ребро играет роль единой стороны прилегания пары боковых граней.
- Высота h представляет собой перпендикулярный отрезок прямой, обозначающий расстояние между парой оснований. Когда ребра по бокам призмы перпендикулярны рассматриваемым основаниям, считают, что такие ребра приобретают смысл высот геометрической фигуры.
- Диагональ основания изображена в виде отрезка, соединяющего пару вершин, расположенных друг напротив друга на едином основании. На изображении диагонали обозначены отрезками \(AC, BD, A_{1}C_{1} и B_{1}D_{1}\). Если речь в задаче идет о треугольной призме, то диагональ отсутствует.
- Диагональ боковой грани представляет собой отрезок, соединяющий пару вершин, которые расположены напротив друг друга и принадлежат одной грани. В геометрической фигуре, рассмотренной на графическом изображении, роль данных элементов играют отрезки \(CD_{1} и C_{1}D\).
- Диагональ призмы является отрезком, с помощью которого соединены две вершины, принадлежащие неодинаковым основаниям и разным боковым граням. В качестве примера таких компонентов геометрического объекта можно привести фрагменты прямых \(AC_{1} и B_{1}D\).
- Поверхность призмы является суммой поверхности пары оснований рассматриваемой фигуры и ее граней, расположенных по бокам.
Виды
Ранее была рассмотрена одна из самых простых разновидностей призмы. Существуют и другие конфигурации данного геометрического объекта. Ознакомимся с распространенными типами фигур, в основании которых треугольник. Начнем с прямой призмы. Таковой является объект с боковыми гранями, которые перпендикулярны относительно основания. Высота в прямой призме соответствует по величине ребру, расположенному сбоку. Ниже представлена типичная прямая призма.
Выделяют в отдельную категорию следующую разновидность призмы, называемой наклонной. В отличие от предыдущего типа геометрического объекта здесь предусмотрено другое расположение боковых граней относительно оснований. Рассматриваемые отрезки не перпендикулярны относительно друг друга, а находятся под каким-либо углом.
Как можно догадаться из названия, в основаниях правильной призмы расположены правильные многоугольники. В то же время этот геометрический объект способен обладать признаками прямой или наклонной фигуры. Представим на рисунке ниже описанную форму для наглядности:
Существует вид призмы, который получен путем некоторых действий. Так, например, при пересечении геометрического объекта какой-либо плоскостью, остается отдельный фрагмент, которому также свойственно определенная форма. Если используемая в процессе плоскость расположена не параллельно по отношению к основаниям призмы, то в результате получается ее часть, которую называют усеченной призмой. Как и в предыдущем примере, полученный путем несложных построений объект может быть отнесен к формату прямой или наклонной призмы. На рисунке для лучшего восприятия изображены оба варианта.
Что такое призма
В жизни человека окружает множество геометрических фигур. Навыки определения их параметров являются полезными. В случае каждого объекта предусмотрены определенные правила и закономерности, которые значительно упрощают решение прикладных и теоретических задач. Одной из сложных и интересных фигур с точки зрения науки геометрии считают призму. Задания на вычисление сторон, площади, объема и прочих характеристик подобного объекта часто попадаются в контрольных и самостоятельных работах. Начнем с основного понятия этого геометрического объекта.
Призмой называют в геометрии пространственную фигуру в виде многогранника с парой параллельных и равных между собой граней, которые являются многоугольниками, и прочими гранями, имеющими форму параллелограммов.
Разобраться со сформулированным определением достаточно сложно. По этой причине целесообразно трансформировать определение в графический рисунок. На изображении, представленном ниже, расположена четырехугольная призма. По-другому этот объект принято именовать параллелепипедом.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Тесты
Тест по теме: «Прямоугольный параллелепипед»
Вариант №1
Уровень А
1. Развёрткой прямоугольного параллелепипеда является фигура под номером…
2.
3. Все шесть граней прямоугольники …
1) у наклонного параллелепипеда;
2) прямого параллелепипеда;
3) прямоугольного параллелепипеда.
4. В прямоугольном параллелепипеде неверно, что…
1) диагонали параллелепипеда равны;
2) диагонали всех боковых граней равны;
3) диагонали оснований равны.
5.
6.
7. Какое утверждение неверное?
1) Куб – это прямоугольный параллелепипед с равными рёбрами.
2) Если в параллелепипеде все рёбра равны, то он является кубом.
3) Не могут боковые грани куба быть не квадратами.
8.
Уровень B
Вариант №2
Уровень А
1. Не является развёрткой прямоугольного параллелепипеда фигура под номером…
2.
3. Четыре грани – прямоугольники, а две – параллелограммы…
1) у наклонного параллелепипеда;
2) прямого параллелепипеда;
3) прямоугольного параллелепипеда.
4. Только в прямоугольном параллелепипеде верно, что…
1) противоположные грани равны и параллельны;
2) диагонали пересекаются в одной точке и делятся в ней пополам;
3) диагонали равны.
5. Какое предложение верное?
1) Всякие два диагональных сечения прямоугольного параллелепипеда пересекаются по его диагоналям.
2) В прямоугольном параллелепипеде все диагональные сечения равны.
3) В прямоугольном параллелепипеде все диагональные сечения – прямоугольники.
6.
7. Какое утверждение верное?
1) Не могут боковые грани прямоугольного параллелепипеда быть не прямоугольниками.
2) Прямоугольный параллелепипед – это куб.
3) Боковыми гранями куба не могут быть прямоугольники с равными смежными сторонами.
8.
Уровень B
Тест по теме: «Призма
Вариант №1
Уровень A
1. Призма изображена на рисунке…
2. 6 – это число…
1) вершин шестиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
3. Не существует призмы, у которой все грани…
1) ромбы;
2) прямоугольники;
3) треугольники.
4. Существует призма, которая имеет…
1) 13 рёбер; 2) 14 рёбер; 3) 15 рёбер.
5.
6.
7. Развёрткой наклонной призмы является фигура под номером…
Уровень B
1. В правильной четырёхугольной призме площадь основания равна 144 см2, а высота равна 14 см. Тогда длина диагонали этой призмы…
2.
3.
Вариант №2
Уровень А
1. Призма изображена на рисунке…
2. 9 – это число…
1) вершин девятиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
3. Не существует призмы, у которой все грани…
1) ромбы;
2) квадраты;
3) трапеции.
4. Число рёбер призмы кратно…
1) 5; 2) 2; 3) 3
5.
6.
7. Не является развёрткой правильной призмы фигура под номером…
Уровень В
Площадь поверхности призмы
После того, как сформировано понимание об основных элементах призмы и ее разновидностях, целесообразно перейти непосредственно к способам вычисления параметров геометрической фигуры. Стоит начать изучение с формул для выполнения расчетов и математических соотношений, которые предназначены для определения площади поверхности объекта. Запишем общую формулировку для вычисления площади полной поверхности геометрической фигуры:
\(S_{общ} = S_{бок} + 2S_{осн}\)
Если призма является прямой, то определить площадь боковой поверхности такой фигуры несложно, зная периметр основания и величину высоты:
\(S_{бок} = Р_{осн}\cdot h\)
Далее запишем математические соотношения, выражающие закономерности между элементами правильной треугольной призмы, в основании которой лежит равносторонний треугольник:
\(S_{осн} = \frac{a^{2}\sqrt{3}}{4}\)
\(S_{бок} = 3аh\)
\(S_{полн} = 3аh + 2\frac{a^{2}\sqrt{3}}{4} = \frac{a^{2}\sqrt{3} + 6аh}{2}\)
Если в задании по геометрии на расчет площади поверхности призмы речь идет о правильной четырехугольной фигуре с квадратом в основании, то целесообразно воспользоваться следующими формулами. Представим изображение такого геометрического объекта с соответствующими обозначениями и сопроводим рисунок несколькими полезными формулами.
\(S_{осн} = a^{2}\)
\(S_{бок} = 4аh\)
\(S_{полн} = 2a^{2}+ 4аh\)
Рассмотрим следующий случай, который часто встречается в примерах по геометрии. Речь идет о правильной шестиугольной призме, основание которой представлено в виде правильного многоугольника с шестью углами.
\(S_{осн} = \frac{3\sqrt{3}a^{2}}{2}\)
\(S_{бок} = 6аh\)
\(S_{полн} = 6аh + 2\frac{3\sqrt{3}a^{2}}{2} = 6аh + 3\sqrt{3}a^{2}\)
Свойства
Геометрическая фигура, которая обладает всеми признаками призмы, имеет ряд полезных свойств. Такие положения определены закономерностями, связывающими элементы объекта. Путем изучения оснований, сторон, граней и других составных компонентов призмы были получены комбинации, позволяющие значительно упростить расчеты характеристик рассматриваемой геометрической фигуры. Перечислим основные свойства и сопроводим их наглядными изображениями для того, чтобы упростить понимание механизма реализации и применения на практике.
Проанализировать характерные для призмы свойства удобно на примере шестиугольного прямого объекта. Стоит отметить, что описанные ниже закономерности не являются индивидуальными, а имеют универсальный характер применения, то есть подходят для исследования и вычисления параметров любой призмы, независимо от ее разновидности. Начнем с равенства оснований призмы, которые являются многоугольниками.
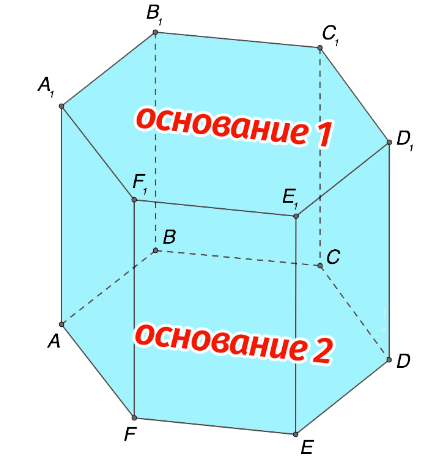
Если ориентироваться на обозначения, сопровождающие рисунок выше, то получим справедливое равенство:
\(ABCDEF = A _{1}B_{1}C_{1}D_{1}E_{1}F_{1}\)
Следующее свойство, характерное ля призмы, заключается в форме граней, расположенных по бокам геометрического объекта. Данные грани являются параллелограммами. Обратимся вновь к ранее представленному изображению и перечислим соответствующие параллелограммы: \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D, DD_{1}E_{1}E, EE_{1}F_{1}F и AA_{1}F_{1}F.\)
Другое полезное свойство призмы заключается в равенстве и взаимной параллельности всех боковых ребер геометрического объекта. Подобную закономерность стоит запомнить, так как это положение часто применяют в процессе решения разнообразных задач в курсе геометрии. Обозначим на графическом рисунке элементы призмы, о которых идет речь, и запишем корректное уравнение для описания примера.
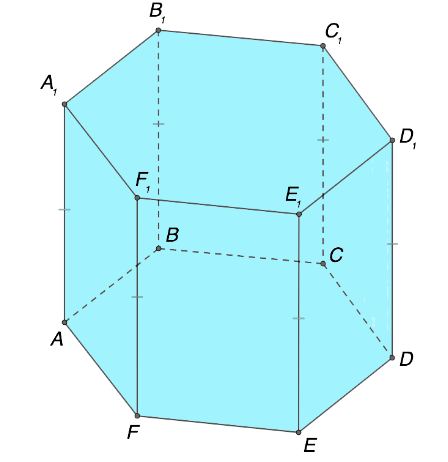
\(AA_{1} = BB_{1} = CC_{1} = DD_{1} = EE_{1} = FF_{1}\)
\(AA_{1} \parallel BB_{1} \parallel CC_{1} \parallel DD_{1} \parallel EE_{1} \parallel FF_{1}\)
Еще одно важное свойство призмы заключается в расположении перпендикулярного сечения. Такая плоскость перпендикулярна относительно всех боковых граней и ребер геометрического объекта
Ознакомиться с прикладным применением данной характеристики можно на изображении ниже:
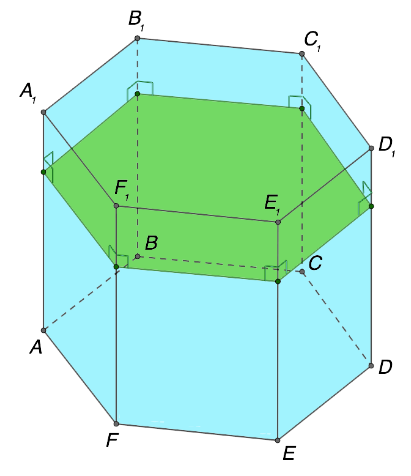
Следующая полезная закономерность состоит в соотношении между высотой и величиной бокового ребра. В какой-либо призме, являющейся наклонной, высота в любом случае будет меньше по сравнению с размером ребра, расположенного сбоку геометрической фигуры. Другая ситуация характерна для прямой призмы. В таком объекте высота по величине соответствует ребру.
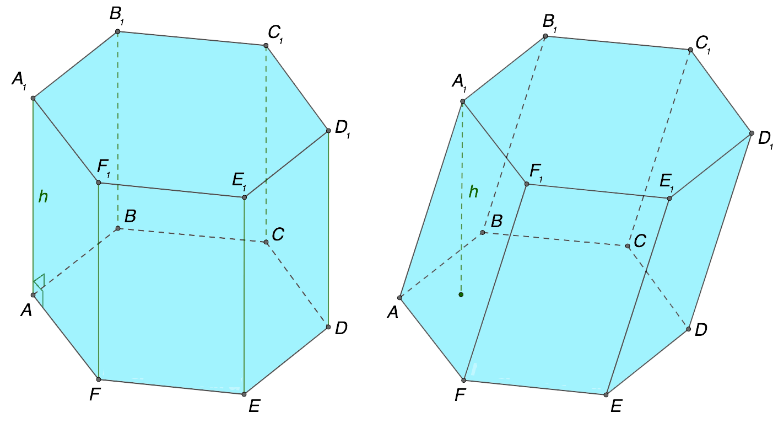
Обращаясь к рисунку выше, допустимо сформулировать справедливые соотношения на примере элементов прямой и наклонной призмы соответственно:
\(h = AA_{1}\)
\(h < AA_{1} \)






























