Базисный минор матрицы как его найти

Определение ранга матрицы.

Определение

Пусть в матрице A существует линейно независимая система из r строк, и нет линейно независимой системы из большего числа строк. Тогда мы будем говорить, что строчный ранг матрицы A равен r. Нулевая матрица не содержит никакой линейно независимой системы строк, и ее строчный ранг по определению равен нулю.

Аналогично определяется столбцовый ранг матрицы. Он равен r_{1}, если есть линейно независимая система из r_{1} столбцов, и нет линейно независимой системы из большего числа столбцов. Столбцовый ранг нулевой матрицы по определению равен нулю.

Утверждение 1.

Система из r строк линейно независима тогда и только тогда, когда в этих строках найдется невырожденная подматрица порядка r.

1^{\circ}. Пусть r строк линейно зависимы. Рассмотрим произвольную подматрицу порядка r, расположенную в этих строках. Если строки линейно зависимы, то также линейно зависимы (с теми же коэффициентами) и отрезки этих строк, составляющие подматрицу, и подматрица является вырожденной.

2^{\circ}. Обратное утверждение докажем по индукции. Одна строка линейно независима, если она не нулевая. В этом случае она содержит ненулевой элемент, составляющий невырожденную подматрицу порядка 1.

Пусть теперь даны r линейно независимых строк. Первые r-1 из них также линейно независимы, и по предположению индукции содержат невырожденную подматрицу порядка r-1. Пусть j_{1},…, j_{r-1} — номера столбцов этой подматрицы. Рассмотрим отрезок r-й строки, расположенный под подматрицей, то есть составленный из элементов с номерами j_{1},…, j_{r-1}. По следствию из этот отрезок раскладывается в линейную комбинацию строк подматрицы. Коэффициенты этой линейной комбинации обозначим \alpha_{1},…, \alpha_{r-1}.

Теперь будем рассматривать полные строки. Вычтем из последней строки линейную комбинацию предыдущих с теми же коэффициентами \alpha_{1},…, \alpha_{r-1}. Это обратит в нуль j_{1},…, j_{r-1}-й элементы r-й строки, но не всю строку, так как строки линейно независимы. Таким образом, в преобразованной r-й строке есть ненулевой элемент a_{j}^{r}, и его номер j отличен от номеров j_{1},…, j_{r-1}.

В преобразованной матрице рассмотрим столбцы, имеющие номера j_{1},…, j_{r-1}, j. (Мы для удобства пишем j на последнем месте, хотя в действительности столбцы располагаются в порядке возрастания номеров.) Легко видеть, что эти столбцы линейно независимы. Действительно, пусть \tag{1} \alpha_{1}\boldsymbol{a}_{j_{1}}+…+\alpha_{r-1}\boldsymbol{a}_{j_{r-1}}+\alpha \boldsymbol{a}_{j}=\boldsymbol{o} их нулевая линейная комбинация. Тогда для последних элементов столбцов \alpha_{1}0+…+\alpha_{r-1}0+\alpha a_{j}^{r}=0. Так как a_{j}^{r} \neq 0, отсюда следует \alpha=0, и мы получаем \alpha_{1}\boldsymbol{a}_{j_{1}}+…+\alpha_{r-1}\boldsymbol{a}_{j_{r-1}}=\boldsymbol{o}. Если бы среди коэффициентов этой линейной комбинации были отличные от нуля, то столбцы с номерами j_{1},…, j_{r-1} были бы линейно зависимы. Это противоречило бы тому, что исходная подматрица порядка n-1 невырождена. Таким образом, все коэффициенты в равны нулю, и столбцы с номерами j_{1},…, j_{r-1}, j линейно независимы. Отсюда следует, что составленная ими подматрица порядка r невырождена.

Невырождена соответствующая подматрица и в непреобразованной матрице, так как элементарными преобразованиями мы превратили ее в невырожденную матрицу. Это заканчивает доказательство.

Определение

В матрице A размеров m \times n подматрица порядка r называется базисной, если она невырождена, а все квадратные подматрицы большего порядка, если они существуют, вырождены.

Столбцы и строки матрицы A, на пересечении которых стоит базисная подматрица, называются базисными столбцами и строками A.

В силу утверждения 1 базисные столбцы и строки линейно независимы.

Определение

Рангом матрицы называется порядок базисной подматрицы или, иначе, самый большой порядок, для которого существуют невырожденные подматрицы. Ранг нулевой матрицы по определению считают нулем.

Отметим два очевидных свойства ранга.

Свойство 1

\bullet Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются, и при этом невырожденные подматрицы остаются невырожденными, а вырожденные — вырожденными.

Свойство 2

\bullet Если A’ — подматрица матрицы A, то ранг A’ не превосходит ранга A, так как любая невырожденная подматрица, входящая в A’, входит и в A.

3.7 Нахождение ранга матрицы

АлгоритмГауссавычислениярангаматрицы.

1. Если
   все

   то rangA = 0.

2. Выбираем
   элемент матрицы

   Помещаем его в левый верхний угол
   матрицы и делим первую строку матрицы
   на

   С помощью элементарных преобразований
   обращаем все элементы первой строки в
   нули:

   .

   Если
   в части матрицы, выделенной синим
   цветом, все

   то rangA = 1.

3. Если
   хотя бы один элемент в области, выделенной
   синим цветом, отличен от нуля, алгоритм
   повторяем. Перестановкой строк и
   столбцов матрицы выбранный элемент

   помещаем на место второго элемента
   второй строки; делим всю вторую строку
   матрицы на этот элемент; элементы второй
   строки, начиная с третьего, обращаем в
   нули. Получим матрицу вида:

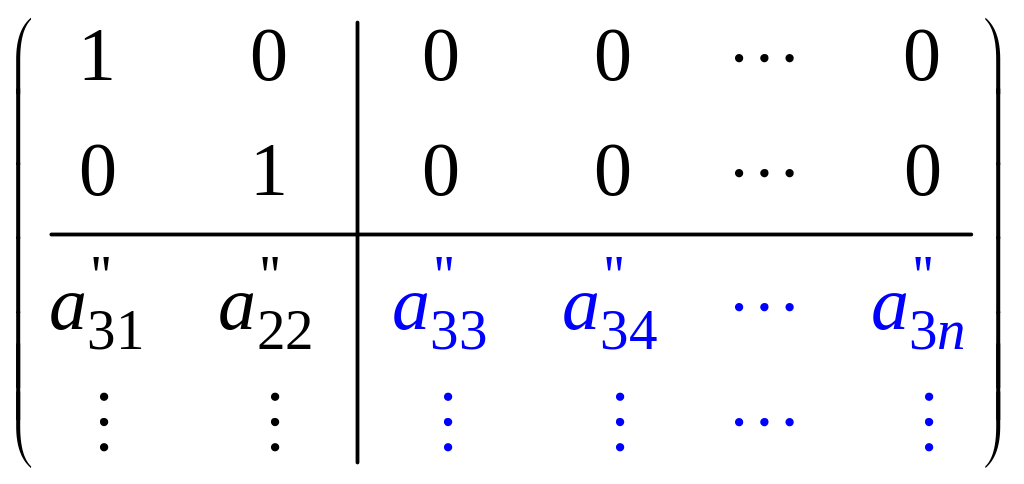
Если
в части этой матрицы, выделенной синим
цветом,

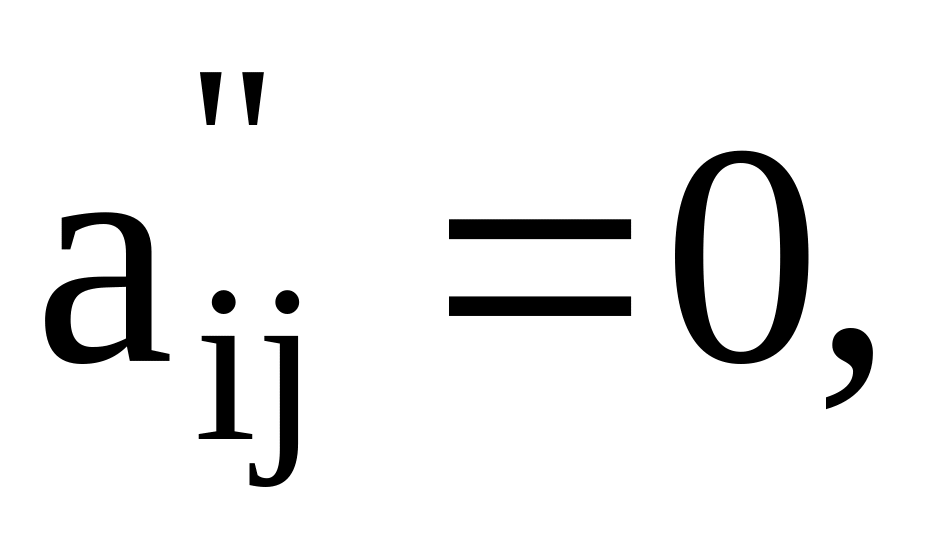
то rang A = 2.

1. Если
   хотя бы один элемент

   в этой области, то алгоритм повторяем.

Послеr
шагов получим матрицу ранга r
вида:

Пример.
Определить ранг и базисный минор матрицы:

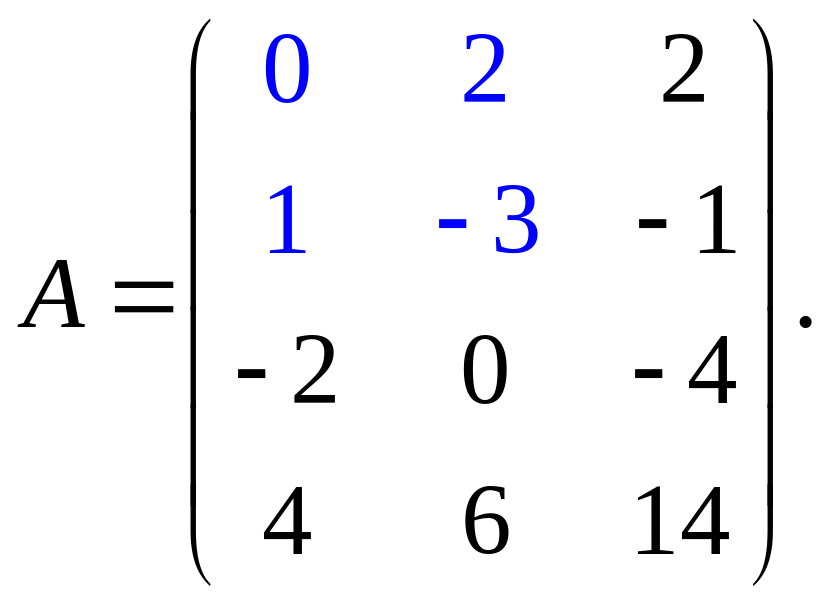
Решение.
Выполним следующие преобразования:
первую, третью и четвертую строки поделим
на 2, затем поменяем местами первый и
второй столбцы:

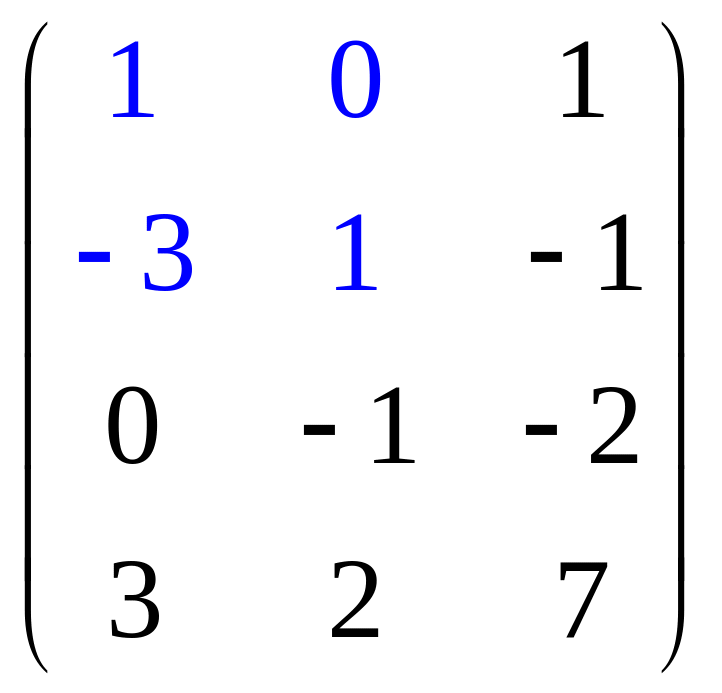
Из
третьего столбца вычтем первый, потом
из него же вычтем второй, умноженный на
два:

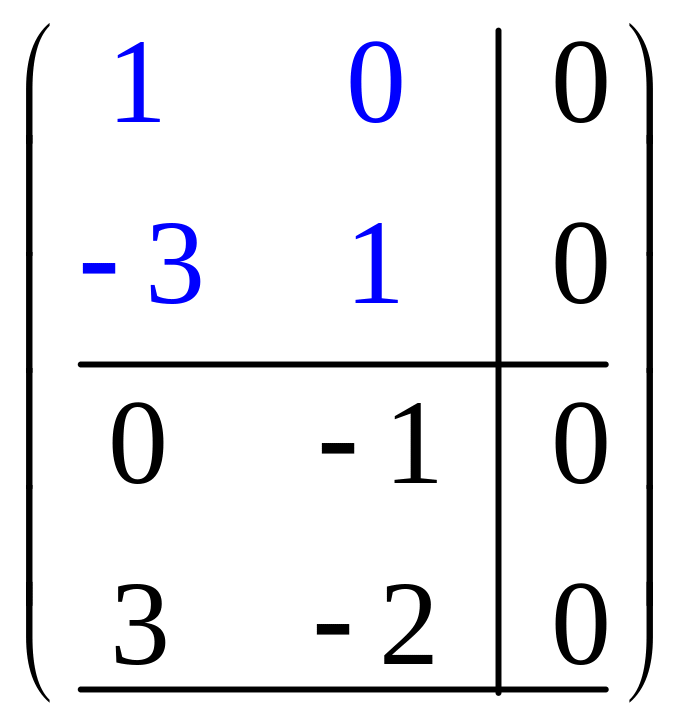
Очевидно,
что ранг последней (а, значит, и исходной)
матрицы равен 2.

Для
того, чтобы определить базисный минор
в исходной матрице, нам необходимо
выделить базисные строки и столбцы. Для
последней матрицы базисный минор выделен
синим цветом. Проходя все действия в
обратном порядке, определим базисный
минор исходной матрицы.

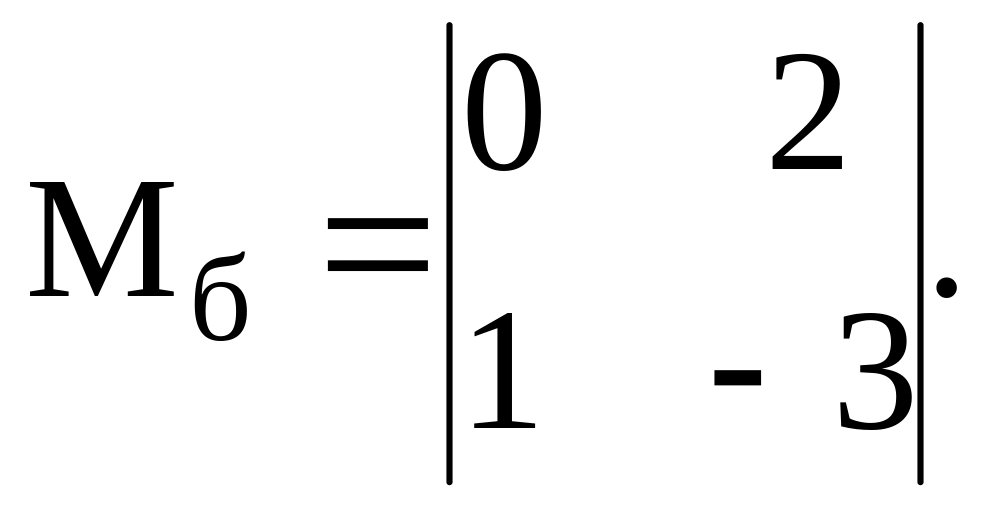
Методокаймляющихминоров.

Определение.
Минор M₁
называется окаймляющим
для минора М, если М получается из M₁вычёркиванием
одной крайней строки (первой или
последней) и одного крайнего столбца.

Теорема.
Если в матрице А размеров

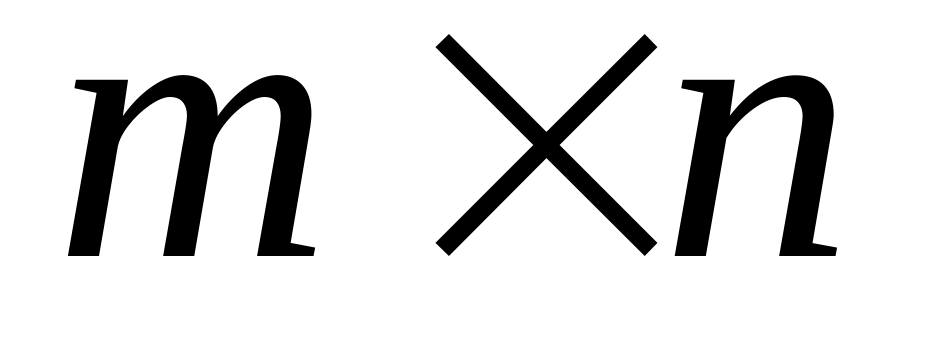
Пример.Для предыдущего
примера:

Вычисляем
минор второго порядка:

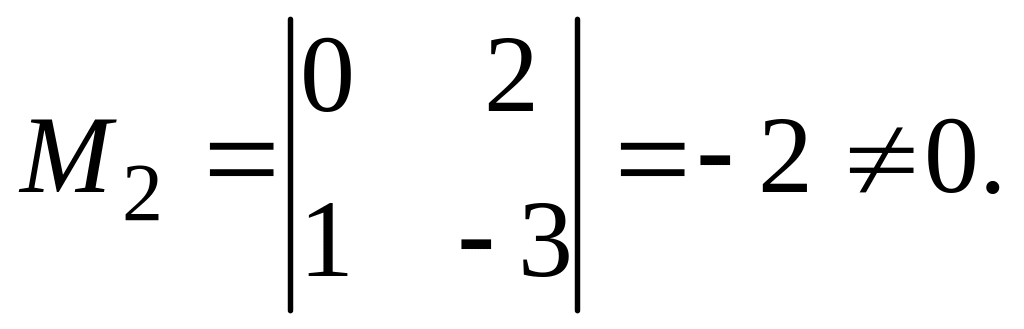
Выбираем
миноры третьего порядка, в которые
входят строки и столбы, дающие предыдущий
минор. Таких миноров всего два:

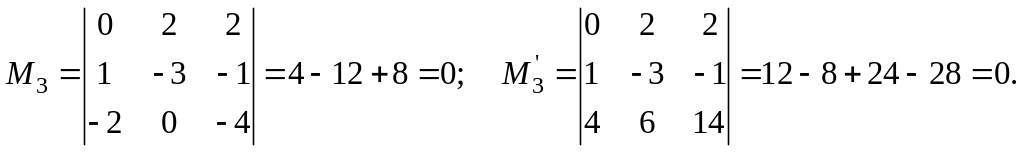
Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Минор матрицы

Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.

Определение 1

Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.

Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.

Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.

Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.

При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2

Другим минором 2-го порядка матрицы А является 0011=0

Предоставим иллюстрации построения миноров второго порядка матрицы А:

Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:

003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9

Иллюстрация, как получается минор 3-го порядка матрицы А:

Для данной матрицы миноров выше 3-го порядка не существует, потому что

k≤min(p, n)=min (3, 4)=3

Сколько существует миноров k-ого порядка для матрицы А порядка p×n?

Число миноров вычисляют по следующей формуле:

Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.

После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.

Использование интернет-калькулятора

В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.

Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.

По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

1. Allcalc — сервис с простым интерфейсом, но в то же время позволяющий выполнить любые действия с матрицей, включая нахождение миноров и алгебраических дополнений.
2. Onlinemschool — сайт, умеющий не только быстро выполнять вычисления, но и выводить пошаговое решение с комментариями.
3. MathSemestr — программное обеспечение калькулятора, понимает даже соотношения, взятые из таких популярных программ, как World и Excel.
4. Pikod — бесплатный сайт, предлагающий получить не только ответ, но и подробно расписанный ход решения.
5. Kontrolnaya-rabota — сервис позволяет выполнять любые преобразования матриц, при этом для сложных заданий существует режим «модульный конструктор».

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.

Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.

Матрицы

Термин «матрица» был введен Дж. Сильвестром в 1850 году, в математику — А. Кэли в 1857 году. Матрицей называется математический объект, состоящий из элементов, взятых в определенном порядке.

Для указания на порядок элементов матрицы их выписывают в виде таблицы из строк и столбцов. Элемент матрицы, стоящий на пересечении строки с номером и столбца с номером обозначают Если — числа, матрица называется числовой. Обозначают матрицы большими латинскими буквами. Обозначение матриц

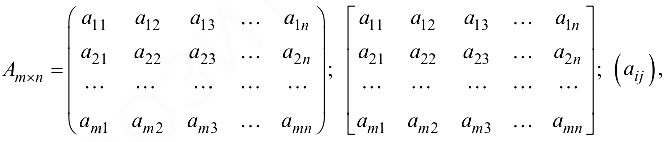
где

Иногда матрицу обозначают одной буквой, например,

Основные виды матриц

Если число строк матрицы равно числу ее столбцов, т. е. то матрица называется квадратной. Порядком квадратной матрицы называется число ее строк (или столбцов). Строки и столбцы матрицы называют ее рядами.

Обозначение квадратной матрицы порядка

— квадратная матрица 3-го порядка.

Две матрицы называются равными, если они имеют одинаковые размеры и элементы одной матрицы равны соответствующим элементам другой матрицы:

В квадратной матрице элементы образуют главную диагональ, а элементы — побочную. Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной Например,

Нулевой матрицей называется матрица, все элементы которой равны нулю:

Симметрическая матрица — квадратная матрица, для которой Например, матрица симметрическая.

Трапециевидная матрица — матрица произвольных размеров, если она имеет вид

где отличны от нуля.

Треугольная матрица (частный случай трапециевидной) -квадратная матрица, все элементы которой по одну или другую сторону от главной диагонали равны нулю. Различают верхнюю и нижнюю треугольные матрицы. Например, матрица вида

называется верхней треугольной матрицей.

Матрица полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной.

Если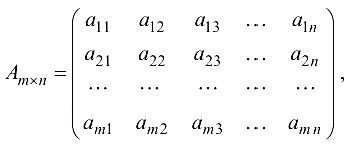

то

Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы. Матрица, состоящая из одной строки, называется матрицей-строкой. Она имеет вид Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Имеет вид

Действия над матрицами

К линейным операциям над матрицами относятся умножение матрицы на число, сложение матриц.

1. Умножение, матрицы на число. Произведением матрицы на действительное число называется новая матрица где Обозначение: Например,

Матрица вида называется матрицей, противоположной матрице

Сложение, матриц

Складывать можно только матрицы одинаковых размеров, т. е. имеющие одинаковое число строк и столбцов.

Суммой двух матриц и называется матрица где и обозначается

Пример №1.1.

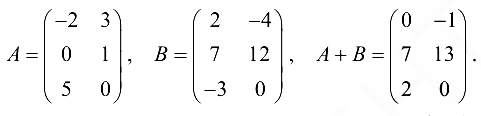
Разность матриц определяется так:

Умножение, матриц

Матрицу будем называть согласованной с матрицей если число столбцов матрицы равно числу строк матрицы

Пример №1.2.

Пусть

Матрица согласована с матрицей но матрица не согласована с матрицей

Если матрица согласована с матрицей то произведением матрицы на матрицу называется новая матрица такая, что

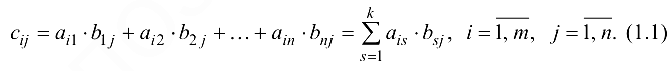
Формула (1.1) называется правилом произведения матриц. Из определения произведения матриц следует, что для того, чтобы получить элемент произведения матриц стоящий в строке и столбце, нужно умножить элементы строки матрицы на соответствующие элементы столбца матрицы и эти произведения сложить.

Пример №1.3.

Вычислить если

Решение:

Матрица (три столбца) согласована с матрицей (три строки).

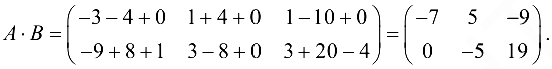
Замечание. Умножить матрицу на в данном случае нельзя — число столбцов матрицы (три) не равно числу строк матрицы (двум).

Замечание. Так как в общем случае то произведение матриц не коммутативно.

Лекция 6. Раздел 6.3Базисный минор и ранг матрицы.

Введя понятие линейной комбинации строк и столбцов матрицы, как это было сделано у векторов, можно ввести понятие их линейной зависимости и независимости.

Определение 6.3.1. Строки , . называются линейно зависимыми, если существуют такие числа , не все равные нулю, что справедливо равенство .

Здесь 0 – нулевая строка.

Определение 6.3.2. Строки называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что .

В этом случае линейная комбинация называется тривиальной.

Так же как и у векторов имеется соответствующая теорема.

Теорема 6.3.1. Для того чтобы строки были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных.

Доказательство проводится так же, как и в п. 1.4.

Теорема 6.3.2. Если в систему строк матрицы входит нулевая строка, то эти строки линейно зависимы.

Доказательство. Действительно, нулевая строка представляет собой тривиальную линейную комбинацию любых строк. Но тогда мы сразу переходим к теореме 1.

Рассмотрим теперь понятие базисного минора. Пусть имеется произвольная матрица порядка :

.

Определение 6.3.3. Минором -го порядка матрицы называется определитель -го порядка с элементами, лежащими на пересечении любых строк и столбцов матрицы .

Определение 6.3.4. В матрице , порядка , минор порядка называется базисным, если он не равен нулю, а все остальные миноры порядка равны нулю или миноров порядка вообще нет, то есть совпадает с меньшим из чисел или .

Очевидно, что в матрице может быть несколько базисных миноров, но все они должны быть одного порядка.

Определение 6.3.5. Рангом матрицы называется порядок базисного минора.

Обозначается ранг матрицы – . Строки и столбцы, на пересечении которых стоят элементы базисного минора, называются базисными.

Теорема 6.3.3. (Теорема о базисном миноре). Базисные строки и столбцы линейно независимы. Любая другая строка или столбец матрицы являются линейной комбинацией базисных строк или столбцов.

Доказательство проведем для строк. Покажем вначале, что базисные строки линейно независимы. Если бы они были линейно зависимы, то одна из этих строк была бы линейной комбинацией остальных. Тогда на основании свойств определителя эту комбинацию можно вычесть из указанной строки и получить на ее месте ноли. Но если вся строка состоит из нолей, то минор равен нулю, что противоречит теореме.

Докажем вторую часть этой теоремы. Рассмотрим любой минор -го порядка, включающий в себя базисный. Расположим базисный минор в левом верхнем углу:

.

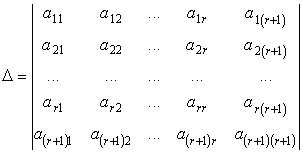По определению данный минор равен нулю. Раскроем его по последнему столбцу:

.

Здесь , разделим на него все равенство:

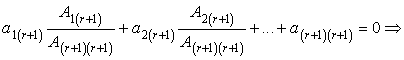
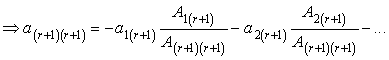
Из полученного выражения следует, что -ая строка является линейной комбинацией базисных строк.

Отсюда можно сделать вывод, что число линейно независимых строк или столбцов равно рангу матрицы. Это свойство используется для практического вычисления .

Ранг матрицы

Минор матрицы. Ранг матрицы. Базисный минор. Линейная зависимость и линейная независимость строк и столбцов матрицы. Критерий линейной зависимости. Теорема о базисном миноре и ее следствия. Инвариантность ранга матрицы относительно ее элементарных преобразований. Способы вычисления ранга матрицы.

Определение 12.1. Минором порядка к матрицы A типа m×n называют определитель, который составлен из элементов этой матрицы, стоящих на пересечении произвольно выбранных к строк и к столбцов с сохранением порядка этих строк и столбцов.

Если выбранные строки имеют номера i1, i2, … , ik, а столбцы — j1, j2, …, jk, то соответствующий минор будем обозначать Мj1, j2, …, jki1, i2, … , ik.

О миноре Мj1, j2, …, jki1, i2, … , ik говорят, что:

— строки i1, i2, …, ik и столбцы j1, j2, … , jk матрицы входят в него;

• — он образован этими строками и столбцами;
• — он располагается на пересечении этих строк и столбцов;
• — он располагается в этих строках и столбцах матрицы.

Строки, входящие в минор, попарно различны, и в обозначении минора естественно упорядочить их по возрастанию номеров. Это же относится и к столбцам.

Правило возрастания номеров означает, что, например, М3,5,61,3,4 является минором некоторой матрицы, расположенным на пересечении 1-й, 3-й и 4-й строк с 3-м, 5-м и 6-м столбцами, в то время как M3,5,61,3,4 минором не является, потому что нарушен порядок столбцов (5-й столбец указан в верхних индексах перед 3-м).

Итак, мы следуем соглашению, что обозначение Мj1,j2. …jki1,i2. …ik соответствует минору матрицы, если верхние и нижние индексы в нем строго возрастают. В противном случае, если индексы расположены в ином порядке, это обозначение соответствует определителю, который получается из соответствующего минора перестановкой строк и столбцов.

Пример 12.1 У квадратной матрицы третьегь порядка девять миноров первого порядка, девять миноров второго порядка и один минор третьего порядка.

Определение 12.2. Рангом матрицы называют число, которое равно максимальному порядку среди ее ненулевых миноров.

Для ранга матрицы A используют обозначение Rg A.

Если квадратная матрица порядка n невырождена, то ее ранг равен ее порядку n: ненулевым является единственный минор максимального порядка n, совпадающий с определителем матрицы. В частности, ранг единичной матрицы E порядка n равен n.

Если квадратная матрица вырождена, то ее ранг меньше ее порядка: единственный минор максимального порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок. Ранг нулевой матрицы полагают равным нулю.

Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов.

Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его характеризующее.

Свойство 12.1. Если ранг матрицы равен r, то матрица имеет хотя бы один минор порядка r, не равный нулю, а все ее миноры больших порядков равны нулю.

Теорема 12.1. При транспонировании матрицы ее ранг не меняется, т.е. Rg AT = Rg A.

Если мы покажем, что при транспонировании матрицы A ее ранг r не убывает, т.е. Rg AT ≥ r, то сможем прийти к следующему заключению. Поскольку (AT)T = A, то r = Rg A ≤ Rg AT ≤ Rg(AT)T = Rg A = r, и поэтому Rg AT = r.

Итак, докажем, что Rg AT ≥ r. Согласно определению 12.2 ранга матрицы, существует ее минор порядка r, отличный от нуля. Пусть это будет минор M = j1,j2. …jki1,i2. …ik. При транспонировании строки и столбцы меняются местами. Поэтому минору M, образованному строками i1, i2, … , ir и столбцами j1, j2, …

, jr матрицы A, соответствует минор N = Nj1,j2. …jki1,i2. …ik матрицы AT, образованный строками j1, j2, … , jr и столбцами i1, i2, … , ir. Ясно, что эти миноры получаются один из другого операцией транспонирования. Согласно свойствам определителей, они равны.

Таким образом, найден минор r-го порядка в матрице AT, а именно минор N, который не равен нулю. Следовательно, Rg AT ≥ r. ►

Теорема 12.2. Ранг матрицы не меняется при элементарных преобразованиях ее строк и столбцов. #

• Строки и столбцы матриц можно рассматривать как матрицы-строки и, соответственно, матрицы-столбцы. Поэтому над ними, как и над любыми другими матрицами, можно выполнять линейные операции.Подробнее
• Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.Подробнее
• Для вычисления ранга матрицы применяют два метода: метод окаймляющих миноров и метод элементарных преобразований.Подробнее

Формулы для определителя

1. Если матрица невырожденная, то и (произведение ведущих элементов).

Знак плюс или минус дается определителем матрицы (или ) и зависит от того, является число перестановок строк в приведении четным или нечетным. Для треугольных сомножителей имеем и

2. Определитель матрицы может быть вычислен разлоразложением по алгебраическим дополнениям i-й строки:

.

Алгебраическое дополнение есть определитель подподматрицы , взятый с нужным знаком:

.

Подматрица образуется вычеркиванием i-й строки и j-го столбца матрицы .

3. Правило Крамера: j-й элемент вектора равен , где

В – вектор заменяет собой j-й столбец матрицы .

Пример.

Решение системы

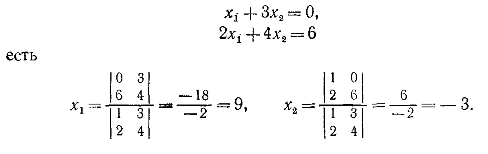
4. Формула для ведущих элементов.

Если матрица представляется в виде , то левые верхние углы удовлетворяют соотношению

Для разных разложения подматриц «согласованы» друг с другом.

Какие строки называются базисными

Индивидуальные онлайн уроки: Отправьте запрос сейчас: [email protected] Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL) Решение задач: по математике, IT, экономике, психологии Теорема о базисном миноре матрицы Учебные дисциплины на сайте Bodrenko.org Портабельные Windows-приложения на сайте Bodrenko.com

§ 3. Теорема о базисном миноре матрицы

Указанные n равенств (1.42) удобно записать в виде одного равенства

Всякий раз, когда будет встречаться равенство (1.43), мы будем понимать его в смысле n равенств (1.42). Введем теперь понятие линейной зависимости строк. Определение. Строки A=(a₁,a₂. a_n), В = (b₁, b₂. b_n). С = (с₁, с₂. с_n) назовем линейно зависимыми, если найдутся такие числа α, β. γ не все равные нулю, что справедливы равенства

Указанные n равенств (1.44) удобно записать в виде одного равенства

а это и означает, что строка А является линейной комбинацией строк В. С. 2) Достаточность. Пусть одна из строк (например, А) является линейной комбинацией остальных строк. Тогда найдутся числа

Минором k-го порядка матрицы А будем называть определитель k- г о порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А. (Конечно, k не превосходит наименьшее из чисел т и п.) Предположим, что хотя бы один из элементов а_ij матрицы А отличен от нуля. Тогда найдется такое целое положительное число r, что будут выполнены следующие два условия: 1) у матрицы А имеется минор r-го порядка, отличный от нуля, 2) всякий минор

(г + 1)-го и более высокого порядка (если таковые существуют) равен нулю. Число г, удовлетворяющее требованиям 1) и 2), назовем рангом матрицы А ( р анг матрицы А, все элементы которой — нули, по определению равен нулю). Тот минор r-го порядка, который отличен от нуля, назовем базисным минором (конечно, у матрицы А может быть несколько миноров r-го порядка, отличных от нуля). Строки и столбцы, на пересечении которых стоит базисный минор, назовем соответственно базисными строками и базисными столбцами. Докажем следующую основную теорему. Теорема 1.6 (теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов). Доказательство. Все рассуждения проведем для строк. Если бы базисные строки были линейно зависимы, то по теореме 1.5 одна из этих строк являлась бы линейной комбинацией других базисных строк, и мы могли бы, не изменяя величины базисного минора, вычесть из этой строки указанную линейную комбинацию и получить строку, целиком состоящую из нулей, а это противоречило бы тому, что базисный минор отличен от нуля. Итак, базисные строки линейно независимы. Докажем теперь, что любая строка матрицы А является линейной комбинацией базисных строк. Так как при произвольных переменах строк (или столбцов) определитель сохраняет свойство равенства нулю, то мы, не ограничивая общности, можем считать, что базисный минор находится в левом верхнем углу матрицы (1.47), т.е. расположен на первых г строках и первых г столбцах. Пусть j — любое число от 1 до n, а k — любое число от 1 до m. Убедимся в том, что определитель (г + 1)-го порядка

(для всех j = 1, 2. n). Учитывая, что в последних равенствах алгебраическое дополнение c_r+1 = A_kj совпадает с заведомо отличным от нуля базисным минором, мы можем поделить каждое из этих равенств на c_r+1. Но тогда, вводя обозначения

Теоремы о базисном миноре и о ранге матрицы

Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.

Действительно, без ограничения общности предполагаем, что в матрице размеров базисный минор расположен в первых строках и первых столбцах. Рассмотрим определитель

который получен приписыванием к базисному минору матрицы соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых и этот определитель равен нулю. Если или , то определитель содержит две одинаковых строки или два одинаковых столбца. Если же r» png;base64,iVBORw0KGgoAAAANSUhEUgAAAC0AAAANBAMAAADPmPqfAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAw0GjIQExURDqgZBhcSAd87kAAACaSURBVBjTY2AgALQasIuzCzugiRyUAlNBMAl2qR5pIMVsEVgAkRBUANOOfXM1DzAw+CnoQcQZWAxVQdT1PAM7oAq9WSkwE1kMQSoO3EtoA1KB716jirNaBoA4CVrzAmDCpSCKdSKI5H7EsBIizmYIsZftFYhklGCVBXOZhCHCDDzPwLLSGxdAhGH+4p4ApkJcwZQy3LscoBABALpmHTnYFagmAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> и r» png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQCAMAAABeF73YAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA5yEQoYcxQcBCsQFxYVHRE4q+egAAAL9JREFUKM+VkuESxBAMhIUkgiLv/7Sn12q563SGfxkr2f3CmNXjUeKC3GZdkZug24qclIeKyb3LBeZhgvZFnXbrWWh6wLOmCLks6E7rtBGkcUKUMNKIToECbId14qTwwwslXA22zM0C6t5CVNpo/gtoEUpfjcvqjeOv9VrhiaTFWq4CNd3UZ5TdTL7TJJDuq0mLhlRHMeMU1Vjt4GJDUtT7CWT086zd+nGgUXcQ5YrqH9ZEF7fjiocP+rBTdzb7APG8BaKqEtq4AAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то определитель равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем

где — алгебраические дополнения элементов последней строки. Заметим, что , так как это базисный минор. Поэтому

Записывая последнее равенство для , получаем

т.е. -й столбец (при любом ) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.

Теорема о базисном миноре служит для доказательства следующих важных теорем.

Ранге произведения и суммы матриц

Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:

В самом деле, пусть матрицы и имеют размеры и . Припишем к матрице матрицу . Разумеется, что , так как — это часть матрицы (см. п.5 замечаний 3.2). Заметим, что каждый столбец , согласно операции умножения матриц, является линейной комбинацией столбцов матрицы

Такой столбец можно вычеркнуть из матрицы , при этом ее ранг не изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы , получаем: . Отсюда, . Аналогично можно доказать, что одновременно выполняется условие , и сделать вывод о справедливости теоремы.

Следствие. Если невырожденная квадратная матрица, то и , т.е. ранг матрицы не изменяется приумножении ее слева или справа на невырожденную квадратную матрицу.

Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:

Действительно, составим матрицу . Заметим, что каждый столбец матрицы есть линейная комбинация столбцов матриц и . Поэтому . Учитывая, что количество линейно независимых столбцов в матрице не превосходит , а (см. п.5 замечаний 3.2), получаем доказываемое неравенство.

Другое определение ранга матрицы

Пусть — система векторов в Rn.

Определение. Рангом данной системы векторов называется максимальное число
линейно независимых векторов в этой системе.

В частности, ранг (или размерность) векторного пространства равен числу элементов базиса этого пространства. Размерность или ранг n-мерного векторного пространства Rn равен n.

Рассмотрим прямоугольную матрицу размера m×n

Столбцы этой матрицы, рассматриваемые как m-мерные векторы, могут, вообще говоря, быть линейно зависимыми.

Определение. Рангом матрицы rank(A) называется ранг системы векторов ее
столбцов.

Теорема . Базисные строки (базисные столбцы) линейно независимы. Любая строка (столбец) матрицы A является линейной комбинацией
базисных строк (базисных столбцов).

Замечание. Теорема о базисном миноре означает, что порядок базисного минора матрицы A равен рангу этой матрицы.

Следствие. Для того, чтобы определитель n-го порядка Δ был равен нулю необходимо и достаточно, чтобы его строки
(столбцы) были линейно зависимы.