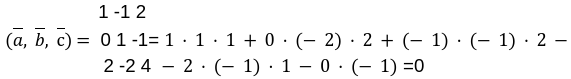Компланарные векторы, исследование системы векторов на компланарность

Использование онлайн-калькулятора

Проверка на условие компланарности обычно не вызывает трудностей в решении примеров из школьного курса. Но на практике, особенно физикам, приходится сталкиваться с большими числами, при этом часто в системе уравнений стоят дробные члены. Поэтому при сложных расчётах благоразумно будет использовать автоматические решатели.

Это такие онлайн-сервисы, которые предоставляют услуги по вычислению различных математических параметров. От пользователя требуется лишь точно ввести в предложенную форму исходные данные и нажать кнопку «Вычислить». Система автоматически рассчитает ответ и выдаст его на дисплей.

1. Onlinemschool.
2. Geleot.
3. Math.semestr.
4. Matematikam.
5. Mathforyou.

Эти сервисы доступны на русском языке. Их страницы не содержат рекламного кода. При этом интерфейс интуитивно понятен.

Для удобства пользователь может включить подробное решение. В таком случае ему будет доступно посмотреть каждое действие, связанное с решением задачи, причём с короткими комментариями. Поэтому онлайн-калькуляторы довольно востребованы как среди школьников, студентов, так и среди инженеров, выполняющих ряд сложных векторных вычислений.

Пример задачи

Пример 1

Пусть нам дан куб $ABCDA_1B_1C_1D_1$. Разложите вектор $\overrightarrow{A_1C_1}$ по векторам $\overrightarrow{AB}\ и\ \overrightarrow{BC}$.

Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ

Решение.

Так как плоскости $(ABC)$ и ${(A}_1B_1C_1)$ параллельны, и векторы $\overrightarrow{A_1C_1}$, $\overrightarrow{AB}\ и\ \overrightarrow{BC}$ параллельны, следовательно, по определению являются компланарными. Тогда, по теореме 1, вектор $\overrightarrow{A_1C_1}$ можно разложить по векторам $\overrightarrow{AB}\ и\ \overrightarrow{BC}$ единственным образом.

Используя свойства сложения двух векторов, получим

\

Так как

\

Следовательно

\

Ответ: $\overrightarrow{AB}+\overrightarrow{BC}$.

Пример 2

Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.

Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

1. Так как векторы $\overrightarrow{OA},\ \overrightarrow{OB}$ и $\overrightarrow{OE}$ лежат в плоскости $(BOA)$ то эти векторы являются компланарными.

2. Так как векторы $\overrightarrow{OC},\ \overrightarrow{OB}$ и $\overrightarrow{{BB}_1}$ лежат в плоскости $(BOC)$ то эти векторы являются компланарными.

3. Так как векторы $\overrightarrow{OC},\ \overrightarrow{OD}$ и $\overrightarrow{OE}$ лежат в плоскости $(COE)$ то эти векторы являются компланарными.

Пример 3

Доказать, что векторы с координатами $\left(1,\ 13,\ 2\right),\ \left(3,\ -5,\ 2\right)и\ (5,-1,4)$ компланарны.

Решение.

Применим признак компланарности трех векторов.

Найдем определитель

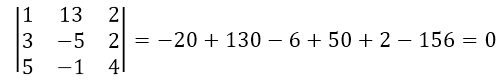Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ

Следовательно, это векторы компланарны, ч. т. д.

Общие условия линейной зависимости векторов

Определение 1. Векторы , , …, называются линейно зависимыми, если найдутся такие вещественные числа ,
из которых хотя бы одно отлично от нуля, что линейная комбинация векторов , , …,
с указанными числами обращается в нуль, т.е. имеет место равенство

.

Векторы , , …, ,
не являющиеся линейно зависимыми, будем называть линейно независимыми.

Определение 2. Векторы , , …, называются линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все числа
равны нулю.

Теорема 1. Если хотя бы один из векторов , , …,
является нулевым, то эти векторы являются линейно зависимыми.

Теорема 2. Если среди n векторов какие-либо (n — 1)
векторов линейно зависимы, то и все n векторов линейно зависимы.

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №18. Компланарные векторы. Векторный метод решения задач

Перечень вопросов, рассматриваемых в теме:

— какие векторы называются компланарными и их изображение на чертежах

-определение компланарных векторов.

— признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

— основы векторного метода решения задач.

Атанасян Л.С. и др. Геометрия. Учебник для 10-11классов — М.: Просвещение, 2017. C. 77-85.

Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь-конспект по геометрии для 10 класса. 2016. С.88-93.

Теоретический материал для самостоятельного изучения:

Давайте вспомним основные определения по теме «Векторы». В этом поможет следующее задание: установите соответствие между понятием и его определением.

Противоположно направлены и их длины равны.

Сонаправлены и их длины равны.

Лежат на одной или параллельных прямых

Появилось новое понятие о векторах в пространстве, которого не было на плоскости — компланарность векторов. С определения компланарных векторов и начинаются главные отличия векторов в планиметрии и стереометрии.

Определение2.Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Рассмотрим некоторые случаи:

1 случай. Любые два вектора всегда будут компланарными, ведь через них можно провести прямые, а через две прямые всегда можно провести единственную плоскость.

2 случай. Три вектора будут компланарными если среди них есть пара коллинеарныхвекторов. Тогда через один из коллинеарных векторов и вектор не коллинеарный ему можно провести плоскость. А для второго из коллинеарных векторов легко изобразить равный в этой плоскости.

3 случай. Если хотя бы один из трёх векторов является нулевым, то эти три вектора компланарны

Из планиметрии: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Следующая теорема выражает признак компланарности трех векторов. Теорема (признак) Если вектор

Для сложения трёх некомпланарных векторов можно пользоваться правилом параллелепипеда. Отложим от произвольной точки О векторы

.

Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Часть 2. Векторный метод решения задач

Векторный метод решения задач – один из наиболее общих методов решения геометрических задач. Векторное решение стереометрических задач значительно проще их решения средствами элементарной геометрии.

Рассмотрим следующую задачу: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

Пусть ABCD — данная трапеция, M и N — середины оснований BC И AD, а O — точка пересечения прямых AB и CD.

Докажем, что точка О лежит на прямой МN.

Условие задачи переводится на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык.

Решением задач векторным методом занимались ученые: Уильман Гамильтон Иога́нн Берну́лли, Пьер Ферма, Рене Декарт, Леонард Эйлер.

Примеры и разбор решения заданий тренировочного модуля:

Задача. В параллелепипеде АВСDА₁В₁С₁D₁ М —точка пересечения диагоналей грани A₁B₁C₁D₁, точка K — середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁ параллельны некоторой плоскости.

Решение. Введем векторы:

Разложим векторы

Тогда векторы

₁₁₁

Источник

Теория. Компланарность векторов

Три вектора называются компланарными

если все они параллельны одной плоскости.

Необходимым и достаточным условием Компланарности трех векторов является равенство нулю их смешанного произведения

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Присоединяйтесь 2011-2023 Довжик Михаил
Копирование материалов запрещено.

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool. com

Три вектора называются компланарными

Общие сведения

Под вектором в математике принято понимать линию, которая имеет начало и конец. Иными словами, это отрезок. При этом имеет значение его направление, то есть знание начальной точки и конечной. Расположение векторов в пространстве или на плоскости определяется их координатами. Они соответствуют проекциям отрезка на координатные оси.

Над отрезками можно выполнять различные действия. Их можно между собой складывать или вычитать, умножать на произвольное число, находить произведение. Последнее может быть скалярным или смешанным. Немаловажным параметром является и длина вектора. Находят её путём вычитания из конечных координат начальных. Если векторов несколько, то на их базе строят геометрические фигуры, с помощью которых находят нужные параметры.

Все векторы разделяют по расположению в пространстве на следующие виды:

1. Единичные — длина отрезка равняется единице. Их принято называть нулевыми, так как конец и начало имеет одну и ту же координату. При этом длина вектора и модуль равны между собой.
2. Коллинеарные — векторы, располагающиеся на одной прямой или параллельные друг другу.
3. Сонаправленные — отрезки с одинаковым направлением.
4. Противоположные — векторы, направленные навстречу друг другу.
5. Компланарные — это линии, параллельные одной плоскости или на ней располагающиеся. При этом так как относительно двух любых векторов будет всегда существовать такая плоскость, то, по сути, они всегда являются компланарными. Отсюда следует, что некомпланарными могут быть только три и более отрезков.
6. Равные — это отрезки, которые не только являются коллинеарными, но ещё имеют и одинаковые длины.

Изображение геометрической проекции отрезков на координатных осях называют расположением по базису. За него чаще всего выбирают координатные орды. При исследовании свойств вначале выполняют графическое изображение, а после переходят к алгебраическому расчёту. Это очень удобно и применяется повсюду.

Линейные комбинации четырёх векторов

Теорема 5. Любые четыре вектора линейно зависимы.

Следствие. Каковы бы ни были некомпланарные векторы , и ,
для любого вектора найдутся такие вещественные числа
, и ,
что справедливо равенство

Пример 1. Составить линейную комбинацию векторов

и

с коэффициентами  и .

Решение. Вычислим сначала произведения и
.
Для этого данные в условии задачи координаты вектора
нужно умножить на 2 (умножаем каждую координату), а координаты вектора
умножить на 3. Получаем:

Теперь находим линейную комбинацию. Для этого первую координату полученного вектора
складываем с первой координатой вектора
, далее вторую со второй, третью с третьей:

Пример 2. Составить линейную комбинацию векторов

с коэффициентами

Аналогично предыдущему находим линейную комбинацию:

Пример 3. Выяснить, являются ли векторы

и

линейно зависимыми.

Решение. В соответствии с определением линейной зависимости нужно найти такие числа и , чтобы

Для этого подставим в последнее равенство координаты векторов и ; тогда

Выполнив в левой части преобразования по правилам действий над векторами, получим

или

Таким образом, вектор

является нулевым и, следовательно, каждая его проекция равна нулю, т.е.

или

Мы получили, что линейная комбинация векторов и может быть нулевой лишь в том случае, если все её коэффициенты равны нулю. Это означает, что данные векторы линейно независимы. 

С понятием линейной независимости векторов и линейной комбинацией связана тема
Базиса системы векторов, которая изучается в отлельном уроке.

Назад

Листать

Вперёд>>>

• Нет времени вникать в решение? Можно заказать работу!
• Пройти тест по теме Векторы

Поделиться с друзьями

Начало темы «Векторы»

• Векторы: определения и действия над векторами
• Сложение векторов: длина суммы векторов и теорема косинусов
• Скалярное произведение векторов

Продолжение темы «Векторы»

• Базис системы векторов. Аффинные координаты
• Векторное и смешанное произведение векторов

4. Теорема о разложении вектора по трем некомпланарным векторам

Любой век­тор в про­стран­стве можно раз­ло­жить по трем за­дан­ным неком­пла­нар­ным век­то­рам, при­чем ко­эф­фи­ци­ен­ты раз­ло­же­ния опре­де­ля­ют­ся един­ствен­ным об­ра­зом.

До­ка­за­тель­ство.

Рис. 5. Раз­ло­же­ние век­то­ра по трем неком­пла­нар­ным

Дано: неком­пла­нар­ные век­то­ры  и , про­из­воль­ный век­тор .

По­стро­им все за­дан­ные век­то­ры из одной точки – точки О (рис. 5). Рас­смот­рим плос­кость, об­ра­зо­ван­ную век­то­ра­ми  и . Из точки Р про­ве­дем пря­мую , па­рал­лель­но на­прав­ле­нию .  – точка пе­ре­се­че­ния плос­ко­сти и пря­мой. Век­то­ры  и  по по­стро­е­нию кол­ли­не­ар­ны, зна­чит имеем: . Те­перь, со­глас­но пра­ви­лу тре­уголь­ни­ка, имеем: . Век­тор  мы нашли. Век­тор  , со­глас­но по­стро­е­нию, лежит в плос­ко­сти век­то­ров  и , зна­чит, со­глас­но тео­ре­ме, рас­смот­рен­ной выше, о раз­ло­же­нии век­то­ра через два некол­ли­не­ар­ных имеем: .

Так, по­лу­че­но раз­ло­же­ние про­из­воль­но­го век­то­ра в про­стран­стве через три  неком­пла­нар­ных век­то­ра: 

До­ка­жем, что такое раз­ло­же­ние един­ствен­но. Ис­поль­зу­ем метод от про­тив­но­го. Пред­по­ло­жим, что есть еще трой­ка чисел (), с по­мо­щью ко­то­рой можно за­дан­ный век­тор раз­ло­жить по трем неком­пла­нар­ным. . Имеем си­сте­му:

Вы­чтем из пер­во­го урав­не­ния вто­рое:

По­лу­чить ну­ле­вой век­тор из трех неком­пла­нар­ных нену­ле­вых век­то­ров путем их сло­же­ния можно толь­ко в слу­чае, когда: , , .

Так, до­ка­за­но, что воз­мож­но един­ствен­ное раз­ло­же­ние век­то­ра по трем неком­пла­нар­ным.

Итак, мы рас­смот­ре­ли по­ня­тие ком­пла­нар­но­сти век­то­ров, до­ка­за­ли тео­ре­мы о раз­ло­же­нии век­то­ров на плос­ко­сти и в про­стран­стве, рас­смот­ре­ли сумму век­то­ров в про­стран­стве.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/vektory-v-prostranstve/komplanarnye-vektory

http://www.mathprofi.ru/vektory_dlya_chainikov.html

http://dok.opredelim.com/docs/index-1592.html

http://www.всёдляшкол.рф/SREDN_SKOOL/MATEM/N110/images/geom_10_13.jpg

http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/

http://www.cleverstudents.ru/vectors/operations_on_vectors.html

Примеры решения задач, для определения компланарности заданных векторов

Для более лучшего восприятия материала, необходимо применить правила компланарности и коллинеарности при решении практических задач. Для этого решим, и подробно распишем три конкретных примера.

Пример №1:

В условии задачи даны три вектора со следующими числовыми значениями.

\;

\;

\.

При условии, что произведение векторов будет равняться нулевому значению, можно сделать вывод о компланарности векторов.

Определяем произведение заданных значений.

Запишем все значения в виде матрицы и решим ее, применяя правила произведения и разности чисел.

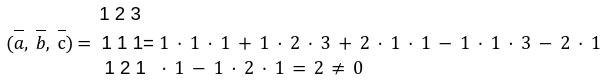
Так как окончательный ответ не равен нулю, а равен значению два. Следует, что вектора не являются компланарными.

Пример №2:

Заданы три вектора с положительными и отрицательными значениями. Необходимо составить и решить матрицу чисел.

\;

\;

\.

Для решения задачи, нужно вычислить произведение значений векторов.

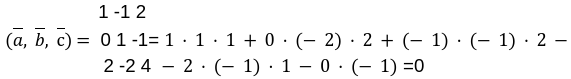
Выполнив все действия по вычислению произведения данных, мы видим, что ответ уравнения равен нулю.

Согласно основному правило компланарности, можно сделать вывод, что вектора ему соответствую. То есть являются компланарными между собой.

Пример №3:

Запишем четыре вектора, со следующими значениями.

Проверим, компланарны ли векторы \ = { 1 ; 1 ; 1 } , \ = { 1 ; 2 ; 0 ) , \ = { 0 ; − 1 ; 1 } , \ { 3 ; 3 ; 3 } .

Начинаем решение примера с преобразования заданных значений и записи их в виде матрицы.

(1    1    1)

(1    2     0)

(0 — 1 1)

(3    3     3)

Далее находим разность между второй и первой строки. Первую умножаем на третью и находим разность полученных значений и четвертой строки. 

(1       1        1)    (1      1       1)

(1-1  2-1   0-1)    (0      1 -1)

(0        -1   1)    (0 -1       1)

(3-3   3-3    3-3)   (0    0      0)

Следующим шагом решения будет сумма третьей и второй строки матрицы.

Составим и запишем следующую матрицу:

(1         1      1)   (1   1    1)

(0         1     -1) — (0   1 (-1))

(0+0  (-1)+1 1+(-1))   ( 0  0    0)

(3-3       3-3      3-3)     (0   0    0)

Проанализировав записанную матрицу, можно сказать, что в ней только две строки с нулевым значением. Следовательно, только два вектора будут компланарны, а остальные нет.

Компланарность в пространстве

Пусть имеются три ограниченных линии в пространстве. Из них можно построить параллелепипед, имеющий общую точку O. Если на плоскости сумма отрезков ищется по правилу треугольника или параллелограмма, то в пространстве используется теорема о многоугольнике. На чертеже следует изобразить диагональ, обозначив её конечную точку буквой F.

Диагональная линия OF по правилу параллелепипеда будет находиться как сумма образующих отрезков: OF = a + b + c. Если в плоскости имеются два неколлинеарных вектора, то можно владеть линиями, принадлежащими ей, то есть третий вектор однозначно разлагается по этим коллинеарным отрезкам. В пространстве же нужны для этого три некомпланарные ограниченные линии.

Этот принцип описывается теоремой: любой четвёртый вектор в пространстве будет равняться сумме трёх отрезков, каждый из которых умножен на конкретное число. Равенство записывают в виде формулы: p = xa + yb + xc. При этом если отрезок можно представить как сложение трёх линий в пространстве, то говорят о его разложении, а числа, используемые в записи, называют коэффициентами разложения. Это необходимое условие для выполнения теоремы.

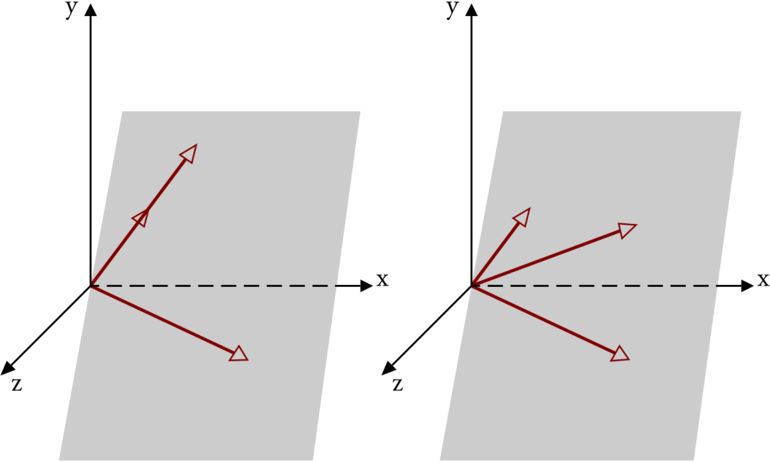
Для доказательства необходимо построить четыре отрезка. Причём a, b, c будут не компланарными, а четвёртая линия будет произвольной в пространстве. Все векторы отложены от одной точки. Выходящие из одной точки a и b образуют плоскость. Из конечной точки P можно опустить перпендикуляр на ось b, тем самым построив прямоугольник. Точка соприкосновения с осью пусть будет P1. Тогда PP1 = zC. Это следует из коллинеарности. Так как P = OP1 + PP1, а OP1 = xa + yb, то, подставив эти выражения линейных комбинаций, можно записать, что P = xa + yb + zc.

Можно утверждать, если существуют такие числа x, y, z, то любую линию, имеющую начало и конец, можно разложить в линейную комбинацию по трём векторам. При этом такое разложение единственное. Проверить это утверждение достаточно просто, если идти от обратного.

Условия компланарности векторов

• Для 3-х векторов выполняется условие: если смешанное произведение 3-х векторов равно нулю, то эти три вектора компланарны.
• Для 3-х векторов выполняется условие: если три вектора линейно зависимы, то они компланарны.
• Для n-векторов выполняется условие: если среди векторов не более 2-х линейно независимых векторов, то они компланарны.

Примеры решения задач на компланарность векторов

Исследуем на компланарность векторы

a ¯ = ( 1 ; 2 ; 3 ) , b = ( 1 ; 1 ; 1 ) и c ¯ = ( 1 ; 2 ; 1 )

Как решить?

Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:

( a ¯ , b ¯ , c ¯ ) = 1 2 3 1 1 1 1 2 1 = = 1 × 1 × 1 + 1 × 2 × 3 + 2 × 1 × 1 — 1 × 1 × 3 — 2 × 1 × 1 — 1 × 2 × 1 = 2 ≠ 0

Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.

Ответ: векторы не являются компланарными.

Докажем, что три вектора

a ¯ = ( 1 ; — 1 ; 2 ) , b = ( 0 ; 1 ; — 1 ) и c ¯ = ( 2 ; — 2 ; 4 ) компланарны.

Как решить?

Находим смешанное произведение данных векторов:

( a ¯ , b ¯ , c ¯ ) = 1 — 1 2 0 1 — 1 2 — 2 4 = = 1 × 1 × 4 + 0 × ( — 2 ) × 2 + ( — 1 ) × ( — 1 ) × × 2 — 2 × 1 × 2 — ( — 2 ) × ( — 1 ) × 1 — 0 × ( — 1 )

Из данного примера видно, что смешанное произведение равняется нулю.

Ответ: векторы являются компланарными.

Проверим, компланарны ли векторы

Как решить?

Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:

1 1 1 1 2 0 0 — 1 1 3 3 3

Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:

1 1 1 1 — 1 2 — 1 0 — 1 0 — 1 1 3 — 3 3 — 3 3 — 3

1 1 1 0 1 — 1 0 — 1 1 0 0 0

К 3-ей строке прибавляем 2-ю:

1 1 1 0 1 — 1 0 + 0 — 1 + 1 1 + ( — 1 ) 3 — 3 3 — 3 3 — 3

1 1 1 0 1 — 1 0 0 0 0 0 0

Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.

Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.

Этот онлайн калькулятор позволит вам очень просто проверить являются ли три вектора компланарными.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на проверку компланарности трех векторов и закрепить пройденый материал.

• Калькулятор
• Инструкция
• Теория