Вариации и обобщения
Квадратный корень из \displaystyle{ a } определяется как решение уравнения \displaystyle{ x^2=a, } и его в принципе можно определить не только для чисел, но и всюду, где такое уравнение имеет смысл. В общей алгебре применяется следующее формальное определение:
|
Пусть \displaystyle{ (G,\cdot) } — группоид и \displaystyle{ a\in G }. Элемент \displaystyle{ x\in G } называется квадратным корнем из \displaystyle{ \ a, } если \displaystyle{ \ x \cdot x=a }. |
Чаще всего рассматривают такие обобщения в алгебраических кольцах.
Если кольцо есть область целостности, то квадратных корней из ненулевого элемента может быть либо два, либо ни одного. В самом деле, если имеются два корня \displaystyle{ a, b, } то \displaystyle{ a^2=b^2, } откуда: \displaystyle{ (a-b)(a+b)=0 }, то есть, в силу отсутствия делителей нуля, \displaystyle{ a=\pm b }. В более общем случае, когда в кольце имеются делители нуля или оно некоммутативно, число корней может быть любым.
В теории чисел рассматривается конечное кольцо вычетов по модулю \displaystyle{ m }: если сравнение \displaystyle{ x^2 \equiv a \pmod m } имеет решение, то целое число \displaystyle{ a } называется квадратичным вычетом (в противном случае — квадратичным невычетом). Решение указанного сравнения вполне аналогично извлечению квадратного корня в кольце вычетов.
Корни для кватернионов имеют много общего с комплексными, но есть и существенные особенности. Квадратный кватернионный корень обычно имеет 2 значения, но если подкоренное выражение — отрицательное вещественное число, то значений бесконечно много. Например, квадратные корни из \displaystyle{ -1 } образуют трёхмерную сферу, определяемую формулой:
- \displaystyle{ \{ai + bj + ck \mid a^2 + b^2 + c^2 = 1\} \,. }
Для кольца квадратных матриц доказано, что если матрица положительно определена, то положительно определённый квадратный корень из матрицы существует и единственен. Для матриц других типов корней может быть сколько угодно (в том числе ни одного).
Квадратные корни вводятся также для функций, операторов и других математических объектов.
Подобные корни и их приведение
Корни называются подобными, если после приведения их к нормальному виду окажутся одинаковыми как их подкоренные выражения, так и показатели корней.
Примеры:
Корни — подобны. Действительно,
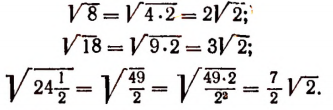
Корни — подобны. Действительно,
Корни подобны. Действительно,
Приведение подобных корней
Примеры:
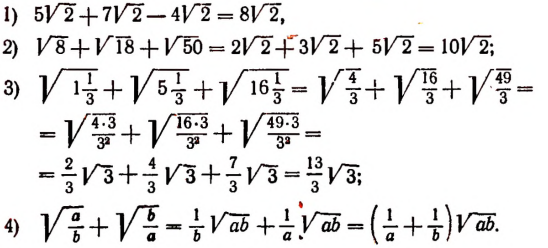
При извлечении корня из суммы нельзя производить извлечение корней из слагаемых, т. е. нельзя писать
Например:
Отсюда видно, что
Преобразование сложного корня
Выражения вида
называются сложными корнями.
Теорема:
Если а > 0, b > 0 и то верны формулы
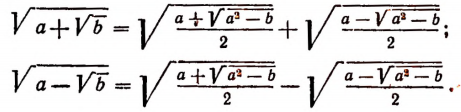
Докажем справедливость первой формулы. Очевидно, что
С другой стороны,
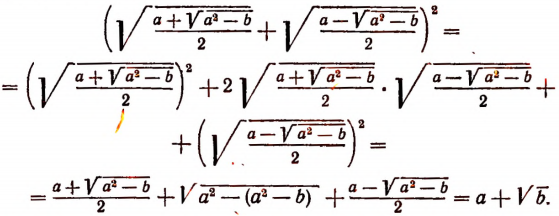
Две величины, порознь равные третьей, равны между собой. Поэтому
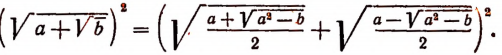
Основания этих квадратов положительны, а поэтому

что и требовалось доказать.
Совершенно так же доказывается и вторая формула. Доказанные формулы представляют особый интерес в том случае, когда разность представляет собой точный квадрат. В этом случае сложный корень представляется в виде суммы или разности двух несложных корней. Например:
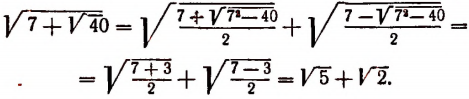
Замечание:
Корни иногда называют радикалами. есть радикал n-й степени. Символ eсть знак радикала n-й степени.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 |
Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
22 = 4; 82 = 64 → 4.
Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Что такое корень квадратный и как его определить
Корень квадратный — это операция, обратная возведению в квадрат. Она позволяет найти число, при возведении которого в квадрат получится заданное число.
Определение корня квадратного можно сформулировать следующим образом:
Корень квадратный числа а — это такое положительное число b, у которого квадрат равен а, то есть b^2 = a. Обозначается корень квадратный числа а как √а.
Определение корня квадратного можно расширить на отрицательные числа:
Корень квадратный отрицательного числа а — это такое положительное число b, у которого квадрат равен модулю числа а, то есть b^2 = |a|. Обозначается корень квадратный отрицательного числа а как √(−а).
Для определения корня квадратного существует несколько способов:
- Геометрический способ: Можно построить квадрат, площадь которого равна заданному числу, и найти длину стороны этого квадрата.
- Алгебраический способ: Можно использовать формулу для корня квадратного или таблицы значений корней квадратных чисел.
Например, для нахождения корня квадратного числа 25 можно использовать следующие способы:
- Геометрический способ: построить квадрат со стороной 5 единиц и найти его сторону.
- Алгебраический способ: использовать формулу для корня квадратного, поскольку √25 = 5.
Таким образом, корень квадратный — это числовая операция, которая позволяет найти число, при возведении которого в квадрат получится заданное число. Он может быть найден с помощью геометрического или алгебраического способа.
Четные и нечетные функции
Функция называется четной, если она обладает следующими двумя свойствами:
- Область определения этой функции симметрична относительно точки О (то есть, если точка принадлежит области определения, то точка также принадлежит области определения).
- Для любого значения , принадлежащего области определения этой функции, выполняется равенство .
- График четной функции – пример.
Функция называется нечетной, если:
- Область определения этой функции симметрична относительно точки O.
- Для любого значения , принадлежащего области определения этой функции, выполняется равенство .
- График нечетной функции – пример.
Заметим, что не всякая функция является четной или нечетной. Например, каждая из функций и не является ни четной, ни нечетной.
Пример 1
Доказать, что функция не является ни четной, ни нечетной.
Доказательство.
Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.
Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что .
Пусть , тогда . Проверяем:
Пример 2
Определите четность или нечетность функции:
Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя). Найдем .
Получим: . Вынесем минус за скобки:
Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция – нечетная функция.
Пример 3
Определить четность или нечетность функции:
Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак аргумента функции и упростим:
Получается, что . То есть функция
5. Решение примеров и работа с графиками
Используем вновь введённое понятие для работы с графиками и решения уравнений.
Снова рассмотрим график функции . Если нам необходимо найти – то это будет абсцисса точки пересечения с данным графиком прямой . Аналогично: – абсцисса точки пересечения с данным графиком прямой , – прямой . (см. рис. 7).
Теперь рассмотрим примеры решения уравнений (систем):
1) . При этом можно вычислять это число приближённо, пользуясь тем, что: , поэтому: . Можно точнее: , поэтому: .
2) . При этом можно вычислять это число приближённо, пользуясь тем, что: , поэтому: .
Рис. 8.
Итак, мы рассмотрели понятие квадратного корня из неотрицательного числа, изучили задачи, из которых оно возникает, а также рассмотрели ряд примеров на вычисление простейших корней и работу с графиками.
На следующем уроке мы более детально изучим работу с квадратными корнями из неотрицательных чисел.
Источник конспекта: http://interneturok.ru/ru/school/algebra/8-klass/funktsiya-y-x-svoystva-kvadratnogo-kornya/ponyatie-kvadratnogo-kornya-iz-neotritsatelnogo-chisla-osnovnye-ponyatiya?konspekt&chapter_id=920
Источник видео: https://www.youtube.com/watch?v=TnVp5BrBjS0
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
| Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a. |
Определение квадратного корня также можно представить в виде формул: √a = x x2 = a x ≥ 0 a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x2 = 16, x = 4 и x = -4.
Что такое арифметический корень натуральной степени
Арифметическим корнем натуральной степени \(n \ge 2\) из неотрицательного числа \(a \ge 0\) называется неотрицательное число, \(n-я\) степень которого равна \(a\).
Поиск корня n-й степени в арифметике называют извлечением корня n-й степени.
Данная операция представляет собой обратное действие возведению в \( n-ю \) степень. В качестве доказательства можно привести следующие примеры:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
\(\sqrt{27} = 3\), так как \(3^3 = 27\)
\(\sqrt{625} = 5\), так как \( 5^4 = 625\)
Квадратные корни из чисел
Рациональные числа
При рациональных \displaystyle{ a } уравнение \displaystyle{ x^2=a } не всегда разрешимо в рациональных числах. Более того, такое уравнение, даже при положительном \displaystyle{ a }, разрешимо в рациональных числах тогда и только тогда, когда и числитель и знаменатель числа \displaystyle{ a }, представленного в виде несократимой дроби, являются квадратными числами.
Непрерывная дробь для корня из рационального числа всегда является периодической (возможно, с предпериодом), что позволяет, с одной стороны, легко вычислять хорошие рациональные приближения к рациональным числам с помощью линейных рекурсий, а с другой стороны ограничивает точность приближения: \displaystyle{ |\sqrt{r}-p/q|\gt \frac{1}{Cq^2} }, где \displaystyle{ C } зависит от \displaystyle{ r }. Верно и то, что любая периодическая непрерывная дробь является квадратичной иррациональностью.
Примеры разложения корней из натуральных чисел от 2 до 10 в непрерывные дроби:
-
\displaystyle{ \sqrt{2} } = \displaystyle{ \sqrt{3} } = \displaystyle{ \sqrt{4} } = \displaystyle{ \sqrt{5} } = \displaystyle{ \sqrt{6} } = \displaystyle{ \sqrt{7} } = \displaystyle{ \sqrt{8} } = \displaystyle{ \sqrt{9} } = \displaystyle{ \sqrt{10} } =
Действительные (вещественные) числа
Для любого положительного числа \displaystyle{ a } существуют ровно два вещественных корня, которые равны по модулю и противоположны по знаку.
Неотрицательный квадратный корень из неотрицательного числа \displaystyle{ a } называется арифметическим квадратным корнем и обозначается с использованием знака радикала: \displaystyle{ \sqrt a }.
Основные свойства вещественного квадратного корня (все значения под знаком корня считаются положительными):
- \displaystyle{ \sqrt{a^2} = |a|: }
- \displaystyle{ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} } (корень из произведения равен произведению корней из сомножителей);
- \displaystyle{ \sqrt{\frac {a} {b}} = \frac{\sqrt{a}} {\sqrt{b}}\quad (b\ne 0); }
К комплексным числам, учитывая двузначность корня, все эти свойства неприменимы (см. ниже пример ошибки).
Комплексные числа
Квадратных корней из любого ненулевого комплексного числа всегда ровно два, они противоположны по знаку. Для корней в комплексной области понятие арифметического корня не вводится, знак радикала обычно либо не используется, либо обозначает не функцию корня, а множество всех корней. В последнем случае, во избежание ошибок, знак радикала не должен использоваться в арифметических операциях. Распространённая ошибка:
- \displaystyle{ -1=(\sqrt{-1})^2 = \sqrt{(-1)^2}=\sqrt{1}=1 } (что, конечно, неверно)
Ошибка возникла из-за того, что комплексный квадратный корень является двузначной функцией, и его нельзя использовать в арифметических действиях.
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
- \displaystyle{ a=|a|e^{i\phi} },
то (см. Формула Муавра)
- \displaystyle{ \sqrt{a}=\sqrt{|a|} \cdot e^{i(\phi+2\pi k)/2} },
где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k = 0 и k = 1, таким образом, в итоге получаются два различных результата.
Существует и чисто алгебраическое представление для корня из \displaystyle{ a+bi }; оба значения корня имеют вид \displaystyle{ \pm(c+di) } где:
- \displaystyle{ c = \sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}} }
- \displaystyle{ d = \sgn (b) \sqrt{\frac{-a + \sqrt{a^2 + b^2}}{2}} }
Здесь sgn — функция «знак». Формула легко проверяется возведением \displaystyle{ c+di } в квадрат.
Пример: для квадратного корня из \displaystyle{ 3+4i } формулы дают два значения: \displaystyle{ 2+i;\; -2-i. }
Квадратный корень как элементарная функция
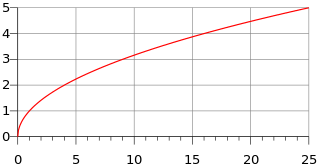
График функции \displaystyle{ y=\sqrt x }
Квадратный корень является элементарной функцией и частным случаем степенной функции \displaystyle{ x^\alpha } с \displaystyle{ \alpha=1/2 }. Арифметический квадратный корень является гладким при \displaystyle{ x\gt 0, } в нуле же он непрерывен справа, но не дифференцируем.
Производная функции квадратного корня вычисляется по формуле:
- \displaystyle{ \frac{d(\sqrt{x})}{dx} = \frac{1}{2\sqrt{x}} }
Как функция комплексного переменного корень — двузначная функция, два листа которой соединяются в нуле (см. подробнее Комплексный анализ).
Графики тригонометрических функций
С чего начинаются тригонометрические мучения в школе? Правильно. С синуса
Построим график функции

Данная линия называется синусоидой.
Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.
Основные свойства функции :
Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.
Область определения: , то есть для любого значения «икс» существует значение синуса.
Область значений: . Функция является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает: или , точнее говоря, бывает, но указанные уравнения не имеют решения.
Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:
Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:, Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.
Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!
В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.
График косинуса
Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси на влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).
Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.
Косинус – это функция четная, ее график симметричен относительно оси , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».
Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .
Графики тангенса и котангенса
Построим график функции

Основные свойства функции :
Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.
Область определения: – все действительные числа, кроме … , , , … и т. д. или коротко: , где – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.
Область значений: . Функция не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси к значению справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси к значению слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .
Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .
В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).
График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.
Что такое арифметический квадратный корень
Заметим, что одним из условий является отсутствие знака минуса у числа а. Попробуем дать этому объяснение. Предположим, что требуется вычислить:
Путем подбора проверим значение 3:
Получилось, что 9 не равно -9. Попробуем взять -3:
В результате нет такого числа, квадрат которого равнялся бы -9. Сделаем вывод об отсутствии чисел, которые при возведении в квадрат дают в итоге число со знаком минус. В связи с этим, выражение, записанное под знаком корня, не должно быть отрицательным, как и само значение арифметического корня.
С другой стороны, рассмотрим уравнение:
Корни в данном случае таковы:
2 и -2.
На первый взгляд, полученное решение противоречит условию, рассмотренному ранее
Однако важно уметь различать между собой квадратное уравнение и арифметический квадратный корень. Например, является квадратным уравнением и не равносильно выражению в виде арифметического квадратного корня
Таким образом, из уравнения вытекает следующее:
Если рассмотреть , то можно сделать вывод, что:
x=2.
Рассмотрим еще один наглядный пример:
Первый вариант записи представляет собой квадратное уравнение с решением:
Второй вариант записи является арифметическим квадратным корнем. При этом:
х = 8.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
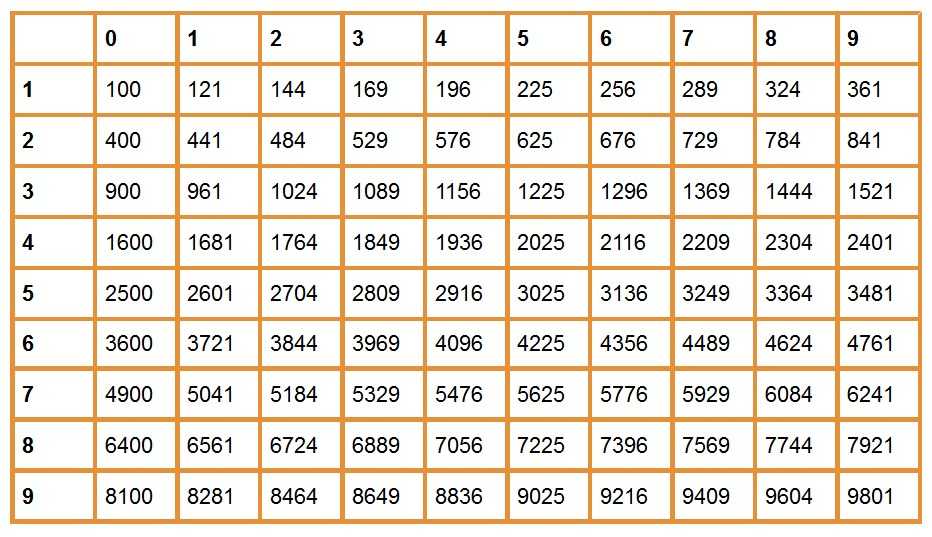
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
102 = 100
202 = 400
302 = 900
402 = 1600
502 = 2500
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 402и 502.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей
12 = 1
22 = 4
32 = 9
42 = 16 ⇒ 6
52 = 25 ⇒ 5
62 = 36 ⇒ 6
72 = 49 ⇒ 9
82 = 64 ⇒ 4
92 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 442 и 462.
Далее вычисляем: 44 * 44 = 1936.
46 * 46 = 2116.
Ответ: √2116 = 46
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
11666 : 4 = 2916
2916 : 4 = 729
729 : 3 = 243
243 : 3 = 81
| 11664 | 4 |
| 2916 | 4 |
| 729 | 3 |
| 243 | 3 |
| 81 | 81 |
Запишем выражение в следующем виде:
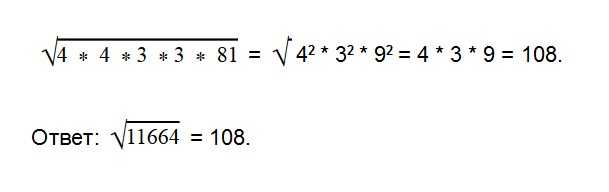
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- Вычислите значение квадратного корня: √36
- Вычислите значение квадратного корня: √64*36
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение выражения: 4√16 — 12
- Вычислите значение выражения: 5√9 — 8
- Вычислите значение выражения: 7√25 — 10
- Вычислите значение квадратного корня:
- Вычислите значение квадратного уравнения:
- Вычислите значение квадратного уравнения:
- Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:7056 4 1764 4 441 3 147 3 49 7 7 7 1 - Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - Вычислите значение квадратного корня:
Как решаем:
= 0,09 - Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - Внесите множитель под знак корня: 6√7
Как решаем: √62 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - Упростите выражение: (5 — √2)2
Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2)2 = 27 — 10√2. - Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
Вычисления, преобразования
Пример 1: Вычислить, преобразовать выражения, содержащие числовые радикалы:
1)$\sqrt{729}=27$
потому, что $27$ именно то единственное положительное число, чей квадрат равен $729$;
2)$\sqrt{75}=\sqrt{3\cdot25}=\sqrt{3}\cdot\sqrt{25}=5\sqrt{3}$
под корнем разложили на множители, увидели полный квадрат числа, извлекли;
3)$\sqrt{2^2\cdot3\cdot7^2\cdot6}=2\cdot7\cdot\sqrt{3\cdot3\cdot2}=2\cdot7\cdot3\cdot\sqrt{2}=42\sqrt{2}$
вынос корня по частям от множителей — полных квадратов; Числа без квадратов «выходят» вперед.
4)$\frac{2}{\sqrt{3}}=\frac{2\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{2\sqrt{3}}{3}$
умножили числитель и знаменатель на радикал, дробь не изменилась. используем $\sqrt{3}\cdot\sqrt{3}=3$;
5)$\sqrt{48}\cdot\sqrt{12}\cdot\sqrt{75}=\sqrt{48\cdot12\cdot75}=\sqrt{8\cdot6\cdot2\cdot6\cdot3\cdot25}=6\cdot5\cdot\sqrt{16\cdot3}=120\sqrt{3}$
в конце вынос квадрата за знак; «если внутри квадрата два одинаковых множителя, из двух выносим один вперед».
6)$\frac{1}{\sqrt{3}-2}=\frac{1\cdot\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\cdot\left(\sqrt{3}+2\right)}=\frac{\sqrt{3}+2}{3-2^2}=-\sqrt{3}-2$
избавили знаменатель от радикала, умножили на сопряженное и числитель, и знаменатель… упростили разность квадратов;
7)$\sqrt{0.81}=\sqrt{\frac{81}{100}}=\frac{\sqrt{81}}{\sqrt{100}}=\frac{9}{10}=0.9$
десятичное число превратили в дробное , использовали свойство радикала от деления;
8)$\sqrt{\frac{64}{225}}=\frac{\sqrt{64}}{\sqrt{225}}=\frac{8}{15}$
свойство радикала от деления. нашли дробь, квадрат которой будет подрадикальной дробью.
Полезные Навыки работы с радикалами:
- «Вынос квадрата за радикал» — если внутри радикала есть множитель — квадрат числа, то само число выносится вперед радикала.
- Если внутри радикала есть два одинаковых множителя (квадрат?), то множителем впереди радикала выносим один из них.
- Если в знаменателе дроби множителем является число с радикалом, то «для избавления» умножаем и числитель и знаменатель на радикал.
- Если в знаменателе сложный радикал (сумма, разность), то «для избавления» умножаем и числитель и знаменатель на сопряженное!
- Примечание: сопряженным к сумме называется разность, и наоборот. Например, сопряженные$a+\sqrt{b}$ и$a-\sqrt{b}$
1. Примеры решения простейшего квадратного уравнения
Цель данного урока – понять, что такое квадратный корень из неотрицательного числа, и в какой ситуации возникла необходимость ввести это новое понятие.
Начнём издалека. Рассмотрим параболу, то есть график функции . При изучении этого графика и его свойств, мы решали две основные задачи: 1) при заданном значении аргумента () получить соответствующее ему значение функции (); 2) при заданном значении функции () получить соответствующие ей значения аргумента ().
Вторая из этих задач и приведёт нас к введению нового понятия.
Рассмотрим следующую задачу.
Пример 1
Решить уравнение: .
Решение:
I способ
Перенесём все выражения в левую часть, получим: .
Ответ: .
II способ
Решим данное уравнение графически. Для этого нарисуем графики двух функций: и . Пересечения этих графиков (точнее, абсциссы точек пересечения) и будут корнями данного уравнения.
Рис. 1.
Мы видим, что графики пересекаются в двух точках, абсциссы которых равны и . Поэтому решение уравнения будет следующим: .
Ответ: .
Решим ещё один аналогичный пример.
Пример 2
Решить уравнение: .
Решение:
I способ
Перенесём все выражения в левую часть, получим: .
Ответ: .
II способ
Решим данное уравнение графически. Для этого нарисуем графики двух функций: и . Пересечения этих графиков (точнее, абсциссы точек пересечения) и будут корнями данного уравнения.
Рис. 2.
Мы видим, что графики пересекаются в двух точках, абсциссы которых равны и . Поэтому решение уравнения будет следующим: .
Ответ: .
Как видим, пока новый термин нам не понадобился.
Извлечение корней
решать примеры с квадратными корнями намного проще, если вы помните как можно больше квадратов чисел. Для этого воспользуйтесь таблицей – сохраните ее себе и используйте для решения задач.
Таблица квадратов
| 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 1600 | 1681 | 1764 г | 1849 г | 1936 г | 2025 | 2116 | 2209 | 2304 | 2401 |
| 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Вот несколько примеров извлечения корня, чтобы научиться пользоваться таблицей:
1. Извлеките квадратный корень:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
Отвечать: .
2. Извлеките квадратный корень:
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
Отвечать: .
3. Извлеките квадратный корень:
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
Отвечать: .
4. Извлекаем рут:
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
Отвечать: .
5. Вытащить корень
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Отвечать: .
извлечение корня называется нахождением его значения.
Действия с корнями: основы
Пример 1
650-28+512
Алгоритм действия:
Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня
Обращаем ваше внимание, что второй множитель заносится под знак корня.
После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений
Нельзя складывать или вычитать подкоренные числа!
Пример 2
Давайте попробуем решить данный пример:
650=6(25×2)=(6×5)2=302. Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.
28=2(4×2)=(2×2)2=42. Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 42.
512=5(4×3)=(5×2)3=103. Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 103.
Результат упрощения: 302-42+103
302-42+103=(30-4)2+103=262+103.
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
Пример 3
(45)+45:
- Упрощаем (45). Раскладываем 45 на множители: (45)=(9×5);
- Выносим 3 из-под корня (9=3):45=35;
- Складываем множители у корней: 35+45=75.
Пример 4
640-310+5:
- Упрощаем 640. Раскладываем 40 на множители: 640=6(4×10);
- Выносим 2 из-под корня (4=2):640=6(4×10)=(6×2)10;
- Перемножаем множители, которые стоят перед корнем: 1210;
- Записываем выражение в упрощенном виде: 1210-310+5;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12-3)10=910+5.
Пример 5
95-23-45
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
(9-4)5-23=55-23.
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3+(2x)1/2.
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Преобразование выражений с квадратными корнями
Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:
Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:
![]()
Обратное действие называют внесением множителя под знак корня:
![]()
Пример. Какое число больше
Решение. Внесем множитель под знак корня:
Из двух корней больше тот, у которого больше подкоренное выражение, поэтому
Из этого следует, что
Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:
Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:
Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула :
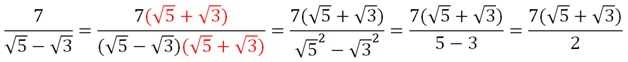
Рассмотрим несколько задач.
Пример. Найдите наибольшее значение выражения
Решение. По формуле разности квадратов можно записать:
Зная это, заменим знаменатель дроби:
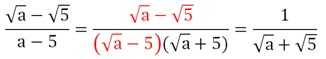
Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять
Пример. Упростите выражение
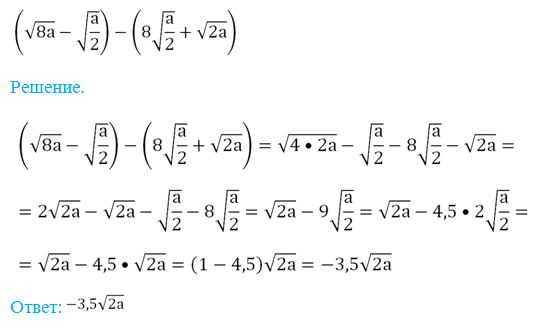
Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида
называют двойным радикалом.
Существует формула двойного радикала, с помощью которой его можно иногда упростить:
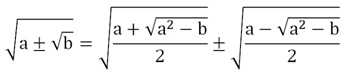
Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя (х ± у)2 = х2 ± 2ху + у2:
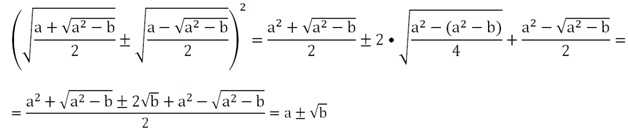
Принципиально важно, что величина а2 – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере. Пусть надо освободиться от внешнего радикала в выражении
Пусть надо освободиться от внешнего радикала в выражении
Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:
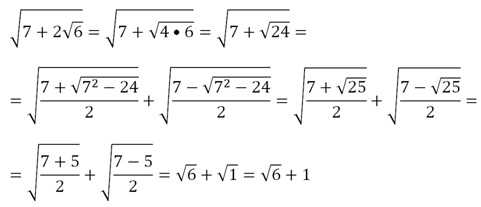
Заметим, что формула двойного радикала полезна в том случае, если выражение а2 – b является полным квадратом.






























