Таблица истинности

Содержание

• 1 Унарные операции
  • 1.1 Логическая истина
  • 1.2 Логическая ложь
  • 1.3 Логическая идентичность
  • 1.4 Логическое отрицание
• 2 Бинарные операции
  • 2.1 Таблица истинности для всех двоичных логических операторов
  • 2.2 Логическая конъюнкция (И)
  • 2.3 Логическая дизъюнкция (OR)
  • 2.4 Логическое следствие
  • 2.5 Логическое равенство
  • 2.6 Исключительная дизъюнкция
  • 2.7 Логическая И-НЕ
  • 2.8 Логическое ИЛИ
• 3 Приложения
  • 3.1 Таблица истинности для наиболее часто используемых логические операторы
  • 3.2 Сжатые таблицы истинности для бинарных операторов
  • 3.3 Таблицы истинности в цифровой логике
  • 3.4 Применение таблиц истинности в цифровой электронике
• 4 История
• 5 Примечания
• 6 См. также
• 7 Ссылки
• 8 Внешние ссылки

Промышленные серии логики

Примеры серии микросхем:ТТЛ − К155, КМ155, К133, КМ133;ТТЛШ − 530, КР531, КМ531, КР1531, 533, К555, КМ555, 1533, КР1533;ЭСЛ − 100, К500, К1500;КМОП — 564, К561, 1564, КР1554;GaAs-К6500;

Каждая серия микросхем, несмотря на то, что она обычно содержит самые разнообразные цифровые устройства, характеризуется некоторым набором параметров, дающих достаточно подробное представление об этой серии. При определении этих параметров ориентируются именно на логические элементы — простейшие устройства серии микросхем. В соответствии с этим говорят о параметрах не серии микросхем, а о параметрах логических элементов данной серии.

Формулы логики высказываний

Понятие логической формы сложного высказывания уточняется с помощью понятия формулы
логики высказываний.

В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания.
Вообще-то они называются формулами логики высказываний.

Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы

Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные
значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее
называть их элементарными формулами или атомами.

Для построения формул логики высказываний кроме указанных выше букв используются знаки
логических операций

~, ∧, ∨, →, ,

а также символы, обеспечивающие возможность однозначного прочтения формул — левая и
правая скобки.

Понятие формулы логики высказываний определим следуюшим
образом:

1) элементарные формулы (атомы) являются формулами логики высказываний;

2) если и —
формулы логики высказываний, то , ,
, ,
тоже являются формулами логики
высказываний;

3) только те выражения являются формулами логики высказываний, для которых это
следует из 1) и 2).

Определение формулы логики высказываний содержит перечисление правил образования
этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется
из атомов в результате последовательного применения правила 2).

Пример 6. Пусть — одиночное
высказывание (атом) «Все рациональные числа являются действительными», —
«Некоторые действительные числа — рациональные числа», —
«некоторые рациональные числа являются действительными». Переведите в форму словесных высказываний
следующие формулы логики высказываний:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Решение.

1) «нет действительных чисел, которые являются рациональными»;

2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;

3) «если все рациональные числа являются действительными, то некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными»;

4) «все действительные числа — рациональные числа и некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными числами»;

5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;

6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».

Пример 7. Составьте таблицу истинности для формулы
логики высказываний , которую в
таблице можно обозначить .

Решение. Составление таблицы истинности начинаем с записи значений («истина» или «ложь»)
для одиночных высказываний (атомов) , и
. Все возможные значения записываются в восемь строк таблицы. Далее,
определяя значения операции импликации, и продвигаясь вправо по таблице, помним, что значение равно «лжи» тогда, когда из «истины» следует «ложь».

И	И	И	И	И	И	И	И
И	И	Л	И	И	И	Л	И
И	Л	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	Л	И	И
Л	И	Л	Л	И	Л	И	Л
Л	Л	И	И	И	И	И	И
Л	Л	Л	И	И	И	Л	И

Заметим, что никакой атом не имеет вида
, ,
, ,
. Такой вид имеют сложные формулы.

Число скобок в формулах логики высказываний можно уменьшить, если принять, что

1) в сложной формуле будем опускать внешнюю пару скобок;

2) упорядочим знаки логических операций «по старшинству»:

, →, ∨, ∧, ~ .

В этом списке знак имеет самую большую область действия, а знак ~ — самую
маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым
применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать
во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при
восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при
этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.

Пример 8. Восстановите скобки в формуле логики высказываний
.

Решение. Скобки восстанавливаются пошагово следующим образом:

Не всякая формула логики высказываний может быть записана без скобок. Например, в
формулах и
дальнейшее исключение скобок
невозможно.

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований
• Пригодится: минимизация логических функций методом Квайна

Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров
являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие
(называемые также вентилями), а также триггер.

С помощью этих схем можно
реализовать любую логическую функцию, описывающую работу устройств компьютера.
Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Чтобы представить два логических
состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы
имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0
вольт.

Высокий уровень обычно
соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).

Каждый логический элемент имеет
свое условное обозначение, которое выражает его логическую функцию, но не указывает
на то, какая именно электронная схема в нем реализована. Это упрощает
запись и понимание сложных логических схем.

Работу логических элементов
описывают с помощью таблиц истинности.

Таблица истинности это
табличное представление логической схемы (операции), в котором перечислены все
возможные сочетания значений истинности входных сигналов (операндов) вместе со
значением истинности выходного сигнала (результата операции) для каждого из
этих сочетаний.

Схемы И, ИЛИ, НЕ, И – НЕ, ИЛИ – НЕ

Схема И

Схема И реализует конъюнкцию двух
или более логических значений. Условное обозначение на структурных
схемах схемы И с двумя входами.

Таблица
истинности схемы И

x	y	x . y
1
1
1	1	1

Единица на выходе схемы И будет
тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на
одном входе будет ноль, на выходе также будет ноль.

Связь между выходом z этой схемы и
входами x и y описывается соотношением: z = x . y (читается
как «x и y»). Операция конъюнкции на структурных схемах
обозначается знаком «&» (читается как «амперсэнд»),
 являющимся сокращенной записью английского слова and.

Схема
ИЛИ

Схема ИЛИ реализует дизъюнкцию
двух или более логических значений. Когда хотя бы на одном входе
схемы ИЛИ будет единица, на её выходе также будет единица.

Условное обозначение на
структурных схемах схемы ИЛИ с двумя входами представлено на рис. 5.2.
Знак «1» на схеме — от устаревшего обозначения дизъюнкции как «>=1»
(т.е. значение дизъюнкции равно единице, если сумма значений операндов больше
или равна 1). Связь между выходом z этой схемы и входами x и y
описывается соотношением: z = x v y (читается как «x или y»).

  Таблица истинности схемы ИЛИ

x	y	x v y
1	1
1	1
1	1	1

Схема
НЕ

Схема НЕ (инвертор)
реализует операцию отрицания. Связь между входом x этой схемы и выходом z
можно записать соотношением z = , x где
читается как «не x» или «инверсия
х».

Если на входе схемы 0, то
на выходе 1. Когда на входе 1, на выходе

  Таблица истинности схемы НЕ

x
1
1

Схема И – НЕ

Схема И – НЕ состоит
из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами x и y схемы записывают
следующим образом: , где читается как «инверсия x и y».

 
                  Рис. 5.4

Таблица истинности схемы
И—НЕ

x	y
1
1	1
1	1
1	1

Схема ИЛИ—НЕ

Схема ИЛИ—НЕ состоит из
элемента ИЛИ и инвертора  и осуществляет отрицание результата схемы
ИЛИ. Связь между выходом z и входами x и y схемы
записывают следующим образом: , где , читается
как «инверсия x или y».

Таблица
истинности схемы ИЛИ—НЕ

x	y
1
1
1
1	1

Основные операции

Количество логических операций, которыми обычно оперирует логика 6:

• Отрицание.
• Умножение.
• Сложение
• Следование.
• Дизъюнкция.
• Равнозначность.

Остановимся на каждом из них детальнее, выясним как правильно они называются в алгебре логики, есть ли у них аналоги в обычной речи, в математике, и как их можно использовать в обычной жизни.

Отрицание или инверсия

Операция отрицания или НЕлогическое, корректнее будет название инверсия.Конечное высказывание будет противоположным первоначальному (исходному). Применяется для одного выражения, которое может быть как сложным, так и элементарным.

На примере этой простейшей операции удобно показывать, насколько лаконичны и информативны таблицы истинности. Обозначим исходное высказывание буквой А, соответственно, окончательное будет не А (или НЕ, ‾, ˥ not А). А их ложность или правдивость напишем при помощи цифр 0 и 1.

Получается, если исходное значение правда, то новое будет ложь, и наоборот.

Умножение или конъюнкция &

Логическое И или умножение еще называют конъюнкцией. Финальное высказывание будет правдивым, только если его составляющие тоже правдивы. Во всех остальных случаях оно будет ложным. Применяется для двух и более аргументов, элементарных или сложных. Обозначение А и В; А ^ В; А &В; A and В.

Как видно, при помощи таблицы истинности из 15 ячеек можно описать то, на описание чего при помощи слов пришлось бы потратить минимум 5 полноценных предложений.

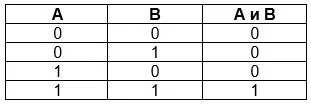
Логическое И в обычной жизни:

• Хорошая певица должна быть талантливой и упорной (наличие только одного качества не позволит проявить миру свой талант).
• По условиям задачи А – число меньше 30, В – число делиться на 3. Нужно найти решение А ˄ В.

Решение: Первое множество содержит числа 1,2,3….29. Второе – 3,6,9,…27. Решением будет множество на пересечении множеств А и В, что хорошо покажут диаграммы Эйлера-Венна. А ˄ В будет истинным для множества чисел 3,6,9,….27.

Сложение или дизъюнкция V

Логическое ИЛИ, сложение по-другому называют дизъюнкцией. Оно истинно всегда, кроме случая, если ложны все составные высказывания. Функция распространяется на простые и сложные исходные аргументы. Обозначение А или В; A v В; А ог В.

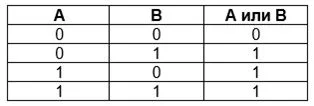
В обычной жизни нас окружает логическое ИЛИ:

• «Чтобы сдать тесты на «отлично», нужно старательно готовиться ИЛИ должно повезти с билетом».
• Есть задача с 2-мя условиями: А – число делится на 5, В – число делится на 2.

Решение: Первое множество чисел включает в себя 5, 10, 15…Второе – 10, 20, 30…Решение, при котором истинно Аv В – совокупность обеих множеств (5, 10, 15, 20, 25, 30…).

Следование или импликация

Для этого случая важно значение каждого выражения и даже его очередность, потому что первый аргумент считается условием, второй – следствием. Импликация будет ложной лишь в одном случае – если первое составляющее правдиво, а второе нет

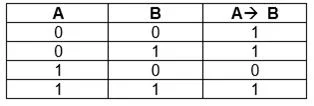
Такое логическое следование имеет аналог в обычной речи «если.. то», то есть одно событие зависит от другого. Символьно связи выражают следующим образом:

Логическое следование в обычной жизни:

• Если пойти к врачу, можно выздороветь (но можно выздороветь и без похода к врачу, а можно и после визита в больницу не выздороветь).
• По условию задачи, А – если число делится на 10, то В делится на 5.

Строгая дизъюнкция

Такая логическая операция выдаст истину, если любое из составляющих высказываний будет истинным, независимо очередности.

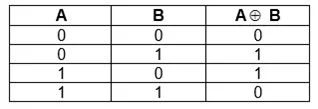
Это пример исключающей функции. Аналог в словесном выражении – «либо». Разница от простой дизъюнкции в том, что конечное выражение будет истинным, только если будет правдой одна переменная.

Эквиваленция или равнозначность 

Операция, выдающая истину в случае, если обе исходные переменные истины или неправдивы.Обозначают А ~В, А  В.

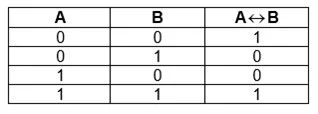
Словесная аналогия – «тогда и только тогда, когда», математическая – «необходимо и достаточно». Если сравнить таблицы истинности для предыдущих операций, очевидно, что она противоположна «исключающему ИЛИ», то ее можно посчитать так:

Пример эквивалентности из обычной жизни:

• Если вечером на горизонте солнце темно-красного цвета, значит, завтра будет ветреный день.
• В задаче 2 условия: А – сумма цифр числа равно 9, В – число делится на 9. АВ означает, что число делится на 9, если сумма цифр равна 9.

Продолжаем знакомиться с законами логики!

Да, совершенно верно – мы с ними уже вовсю работаем:

Формула, которая принимает значение Истина при любом наборе значений входящих в неё переменных,  называется тождественно истинной формулой или законом логики.

В силу обоснованного ранее перехода от равносильности  к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.

Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных,  называется тождественно ложной формулой или противоречием.

Фирменный пример противоречия от древних греков: – никакое высказывание не может быть истинным и ложным одновременно.

Доказательство тривиально:
«На выходе» получены исключительно нули, следовательно, формула действительно тождественна ложна.

Однако и любое противоречие – это тоже закон логики, в частности:

Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:

Закон исключённого третьего

  – в классической логике любое высказывание истинно или ложно и третьего не дано. «Быть или не быть» – вот в чём вопрос.

Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.

Закон контрапозиции

Этот закон активно муссировался, когда мы обсуждали суть необходимого условия, вспоминаем: «Если во время дождя на улице сыро, то из этого следует, что если на улице сухо, то дождя точно не было».

Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.

Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной:

И снова вернёмся к нашим содержательным примерам: для высказываний   – число делится на 4,  – число делится на 2 справедливы прямая и противоположная теоремы, но ложны обратная и противоположная обратной теоремы. Для «взрослой» же формулировки теоремы Пифагора истинны все 4 «направления».

Закон силлогизма

Тоже классика жанра: «Все дубы – деревья, все деревья – растения, следовательно, все дубы – растения».

Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)

Давайте на этой веселой ноте проведём доказательство. В данную формулу входят уже  элементарных высказывания , а значит, всего будет:  различных  комбинаций нулей и единиц (см. три левых столбца таблицы). Заодно, кстати, записал вам общую формулу; с точки зрения комбинаторики, здесь размещения с повторениями.

Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:

1) выполняем импликации  и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;

2) к столбцам  применяем правило И;

3) вот теперь выполняем ;

4) и на завершающем шаге применяем импликацию к столбцам  и .

Не стесняйтесь контролировать процесс указательным и средним пальцем :))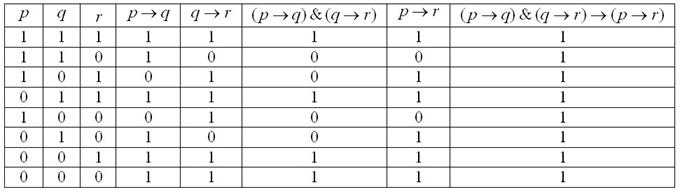
Из последнего столбца, думаю, всё понятно без комментариев:, что и требовалось доказать.

Задание 3

Выяснить, будет ли являться законом логики следующая формула:

Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.

Алгебра логики и решение задач

Несмотря на то, что логика, как наука о размышлении, существовала еще 5 в. До н.э., теперь это важная часть многих наук, а не только философии и риторики. Также логика существует, как отдельная наука уже более 200 лет.

Инструменты алгебры логики позволяют переводить словесные высказывания в сухие, объективные выражения, а с их помощью выполнять различные логические операции.Появился этот раздел математики 200 лет назад.

Стоит остановиться на базовых понятиях алгебры логики:

• константы (0,1);
• переменные;
• формула;
• знаки операций;
• скобки.

Логическая переменная – обозначение логического выражения, которое может быть true (t, правда, истина, да, 1) – false (f, ложь, нет, 0).

Формула– символьный способ выражения операции между переменными при помощи специальных знаков и скобок ().

Логическое высказывание – утверждение, в котором говорится только правда или только ложь.

Образец таких предложений: «Луна – вертится вокруг Марса» – ложно, а «После зимы всегда приходит весна» – истинно.

Частицы «не», «или», если», «и» и другие, которые являются связующими элементами в обычной речи, позволяют создавать элементарные логические выражения.

Элементарные высказывания – те, к которым нельзя применить понятие истинности или ложности. Их обозначают различными символами (латинские буквы, цифры), знаками. Ими занимаются те сферы, к которым они относятся. Они входят в состав высказываний логики.

Из одних высказываний можно образовывать другие, в результате получая составные высказывания. И от того, являются исходные элементы составного конечного высказывания правдивыми или неправдивыми, а также какие логические связки использовались, будет правдой или ложью все высказывание в целом.

Чтобы образовать такое составное предложение в обычной жизни, используют связки И, ИЛИ, НЕ. А научный подход заменил их на конъюнкцию, дизъюнкцию, инверсию и более сложные операции. Все эти процессы выражают словесно, таблично (таблицы истинности) или графически (диаграммы Эйлера-Венна).

Простые выражения содержат лишь одно выражение (правдивое или нет), и не содержит никаких логических операций.

Сложные могут содержать от 2 и больше аргументов (простых выражений), которые между собой связаны логическими операциями.

Еще используют понятие «предикат» – содержит любое количество переменных без перечисления всех составляющих данных. Это предикат простых, отрицательных P(x)=(x<0) чисел.

Чтобы исключить лишнюю информацию, оставив только логические связи, используют таблицы истинности, наглядно демонстрирующие, правдиво или неправдиво конечное предложение, если учесть все значения входящих в его состав простейших частей.

Такая форма оформления и решения задач используется в построении электросхем, для решения различных логических задач, в булевой алгебре, программировании.

3.11. Что такое переключательная схема

В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов: реле,
выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что
здесь с успехом может быть использован аппарат алгебры логики.

Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое. Переключателю Х поставим в соответствие логическую
переменную х, которая принимает значение 1 в том и только в том случае,
когда переключатель Х замкнут и схема проводит ток; если же переключатель
разомкнут, то х равен нулю.

Будем считать, что два переключателя Х и связаны
таким образом, что когда Х замкнут, то
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в
соответствие логическая переменная х, то переключателю должна
соответствовать переменная .

Всей переключательной схеме также можно поставить в соответствие логическую
переменную, равную единице, если схема проводит ток, и равную нулю — если не
проводит. Эта переменная является функцией от переменных, соответствующих всем
переключателям схемы, и называется функцией проводимости.

Найдем функции проводимости F некоторых переключательных схем:

a)  

Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; 

б)  

Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; 

в)  

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F(x) = x; 

г)  

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда
х замкнут, следовательно, F(x) = ; 

д)  

Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; 

е)  

Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; 

ж)  

Схема состоит из двух параллельных ветвей и описывается функцией . 

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И

Журавлев,
С.В. Яблонский и др.

При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём
этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти
   условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к

1. определению значений её функции проводимости при всех возможных наборах
   входящих в эту функцию переменных.
2. получению упрощённой формулы.

Примеры.

1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут
контакт переключателя t и какой-нибудь из остальных трёх контактов.

Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) =
t . (x v y v z), а схема выглядит так:

2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из
этих переключателей.

Схема имеет вид:

3. Найдем функцию проводимости схемы:

Решение. Имеется четыре возможных пути прохождения тока при замкнутых
переключателях a, b, c, d, e : через переключатели a, b; через переключатели a,
e, d; через переключатели c, d и через переключатели c, e, b. Функция
проводимости F(a, b, c, d, e) = a . b   v   a .
e . d   v   c . d   v   c .
e . b.

4. Упростим переключательные схемы:

а)  

Решение:   

Упрощенная схема:

б)  

.

Здесь первое логическое слагаемое является
отрицанием второго логического слагаемого , а
дизъюнкция переменной с ее инверсией равна 1.

Упрощенная схема :

в)  

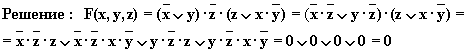
Упрощенная схема:

г)  

Упрощенная схема:

д)  

(по
закону склеивания)

Упрощенная схема:

е)  

Решение: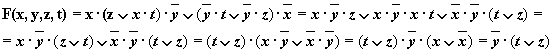

Упрощенная схема:

Аксиомы и законы

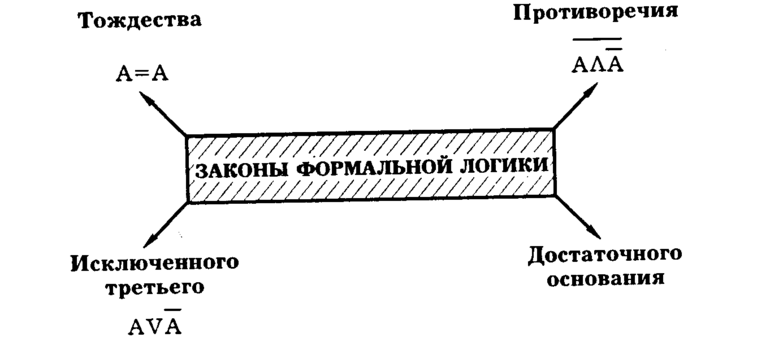
Создание таблиц истинности удобным способом позволяет определить, когда то или иное действие или высказывание приобретает правильное значение, а когда нет. В верхней строке записывается логическая форма высказывания, а в столбцах — точные значения. Некоторые комбинации всегда будут правдивыми или ложными, независимо от содержания. Поэтому были сформулированы следующие принципы:

1. Тождества. Записывается в виде тезиса: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и истинной. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Он означает, что одно понятие нельзя заменить другим, иначе возникнут логические ошибки.
2. Противоречия. Тезис, что А и НЕ-А, ложно: А & А = 0. Другими словами, если А является точным значением, то его отрицание не может быть ложным. То есть их перемножение всегда будет ложным. Он очень часто используется для упрощения сложных логических суждений.
3. Исключения третьего. Записывается как A v A = 1 и означает, что одновременно оно может быть только правдимым или ложным. То есть третьего варианта нет.

Все три являются фундаментальными. Не соблюдая их, невозможно сделать правильное заключение.

Для решения логических задач с помощью таблиц истинности применяются различные формулы, соответствующие разным типам операций. Одним из них является логическое умножение (конъюнкция). В этом случае функция считается правдивой только тогда, когда истинны оба высказывания: F = A & B. Еще одно логическая дизъюнкция говорит, что если они ложны, то и логическая функция будет ложно.

Кроме того, используется принципы:

• инверсии (отрицания) — если логическая цепочка истинна, то ее отрицание будет ложным;
• импликации (следования) — для всегда верного сложного логического высказывания ложь будет тогда, когда из верности получается отрицание;
• равнозначности (эквивалентности) — предложение будет точным только тогда, когда оба имеют одинаковое значение.