Комплексные числа в тригонометрической форме

Алгебраическая форма комплексного числа

действительной частью

Число называется мнимой частью комплексного числа и имеет обозначение .

Например:

1. Комплексное число и его сопряженное число записаны в алгебраической форме.
2. Мнимое число записано в алгебраической форме.

Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в тригонометрическую или показательную форму.

Задание	Записать число в алгебраической форме, найти его действительную и мнимую части, а также сопряженное число.
Решение	Применяя почленное деление дроби и правило сложения дробей, получаем: Следовательно, действительной частью комплексного числа является число , мнимой частью является число . Сопряженное число имеет вид: .
Ответ

Сравнение

Два комплексных числа и называются равными, если , т.е. равны их действительные и мнимые части.

Задание	Определить, при каких и два комплексных числа и являются равными.
Решение	По определению два комплексных числа являются равными, если равны их действительные и мнимые части, т.е. .
Ответ

Сложение

Сложение комплексных чисел и выполняется непосредственным суммированием действительных и мнимых частей:

Задание	Найти сумму комплексных чисел .
Решение	Действительной частью комплексного числа является число , мнимой частью является число . Действительная и мнимая части комплексного числа равны и , соответственно. Следовательно, сумма комплексных чисел равна:
Ответ

Подробнее про сложение комплексных числе читайте в отдельной статье: Сложение комплексных чисел.

Вычитание

Вычитание комплексных чисел и выполняется непосредственным вычитанием действительных и мнимых частей:

Задание	Найти разность комплексных чисел .
Решение	Найдем действительные и мнимые части комплексных чисел : Следовательно, разность комплексных чисел равна:
Ответ

Умножение

Умножение комплексных чисел и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :

Задание	Найти произведение комплексных чисел .
Решение	Произведение комплексных чисел равно:
Ответ

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел и находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

Задание	Разделить число 1 на комплексное число .
Решение	Поскольку мнимая часть вещественного числа 1 равна нулю, частное чисел равно:
Ответ

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Все формы записи комплексных чисел

Тригонометрическая форма КЧ

Показательная форма КЧ

Мнимая часть комплексного числа

Комплексно сопряженные числа

Операции над комплексными числами

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

z = a + bi.

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

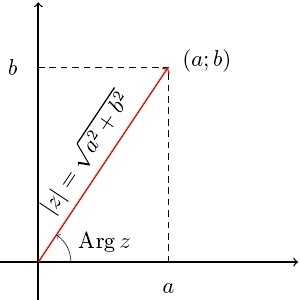
В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

\(\sqrt{a^{2}+b^{2}}\)

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

\(\left|z \right|\)

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

\(z=\left|z \right|*e^{i\varphi }\)

Где \(\left|z \right|\)является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

• изобразить чертеж;
• найти модуль;
• рассчитать аргумент.

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для умножения, деления и возведения комплексных чисел в натуральную степень.

Действительно, умножение и деление двух произвольных комплексных чисел, записанных в экспоненциальной форме, выполняется по формулам

Поэтому при умножении комплексных чисел их модули умножаются и аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разнице между аргументами делимого и делителя.

Возведение комплексного числа z = r и iφ в естественную степень выполняется по формуле

Другими словами, когда комплексное число возводится в степень, которая является натуральным числом, модуль числа повышается до этой степени, а аргумент умножается на показатель степени.

1.Комплексные числа. Свойства. Формы записи.

БИЛЕТ1

Комплексным числом
называется выражение вида ,
где—
действительные числа;—
число, квадрат которого равен минус
единице;
число обозначается.

Свойства
комплексных чисел:

1)
комплексные числа коммутативны по
сложению и по умножению.

2)
комплексные числа ассоциативны по
сложению и по умножению.

3)
комплексные числа дистрибутивны.

Для
комплексных чисел операция деления
определена как операция обратная
операции умножения. Если ,
то z является
решением уравнения .
Решим это уравнение, домножив левую и
правую часть на и
разделив обе части на квадрат модуля.
Получим, что

Формы
записи:

Для
комплексных чисел существует несколько
форм записи: алгебраическая форма
записи, тригонометрическая форма записи
и экспоненциальная (показательная)
форма записи.

Алгебраическая
форма —
это  такая форма записи комплексных
чисел, при которой комплексное число
 z, заданное
парой вещественных чисел   (x
, y),
записывается в виде

где
использован символ   i ,
называемый мнимой
единицей.
Число x называют вещественной
(реальной) частью комплексного числа   z
= x + i y  
и обозначают   Re z.
Число y называют мнимой
частью комплексного числа   z
= x + i y  
и обозначают   Im z.

Тригонометрическая
форма записи комплексного числа

      Из
формулы
вытекает, что любое отличное от нуля
комплексное число  z
= x + i y  
может быть записано в виде

z = r (cos φ + i sin φ) ,

(5)

где  r  и φ —
модуль и аргумент этого числа,
соответственно, причем модуль удовлетворяет
неравенству  r >
0.

Формула
Эйлера. Экспоненциальная форма записи
комплексного числа

Формула
Эйлера:
cos
φ + i sin
φ = e iφ.

Из
формулы Эйлера и тригонометрической
формы записи комплексного числа вытекает,
что любое отличное от нуля комплексное
числоz
= x + i y  
может быть записано в виде

где  r  и φ —
модуль и аргумент этого числа,
соответственно, причем модуль удовлетворяет
неравенству  r >
0.

БИЛЕТ 2.

2.Интегрирование простейших рациональных функций

Для
интегрирования рациональной функции ,
где P(x) и Q(x) —
полиномы, используется следующая
последовательность шагов:

1)Если
дробь неправильная (т.е. степень P(x) больше
степени Q(x)),
преобразовать ее в правильную, выделив
целое выражение;
2)Разложить
знаменатель Q(x) на
произведение одночленов и/или несократимых
квадратичных выражений;
3)Разложить
рациональную дробь на простейшие дроби,
используя метод
неопределенных коэффициентов;

4)Вычислить
интегралы от простейших дробей.

Рассмотрим
указанные шаги более подробно. 

Шаг
1. Преобразование неправильной рациональной
дроби

Если
дробь неправильная (т.е. степень
числителя P(x) больше
степени знаменателя Q(x)),
разделим многочленP(x) на Q(x).
Получим следующее выражение:

где —
правильная рациональная дробь. 

Шаг
2. Разложение знаменателя на простейшие
дроби

Запишем
многочлен знаменателя Q(x) в
виде

где
квадратичные функции являются
несократимыми, то есть не имеющими
действительных корней. 

Шаг
3. Разложение рациональной дроби на
сумму простейших дробей.

Запишем
рациональную функцию в следующем виде:

Общее
число неопределенных коэффициентов A_i,
B_i,
K_i,
L_i,
M_i,
N_i,
… должно
быть равно степени знаменателя Q(x).  Затем
умножим обе части полученного уравнения
на знаменатель Q(x) и
приравняем коэффициенты при слагаемых
с одинаковыми степенями x.
В результате мы получим систему линейных
уравнений относительно неизвестных
коэффициентов A_i,
B_i,
K_i,
L_i,
M_i,
N_i,
….
Данная система всегда имеет единственное
решение. Описанный алгоритм представляет
собой метод
неопределенных коэффициентов. 

Шаг
4. Интегрирование простейших рациональных
дробей.

Простейшие
дроби, полученные при разложении
произвольной правильной рациональной
дроби, интегрируются с помощью следующих
шести формул:

У
дробей с квадратичным знаменателем
сначала необходимо выделить полный
квадрат:

где Затем
применяются следующие формулы:

Интеграл может
быть вычислен за k шагов
с помощью формулы редукции

БИЛЕТ
3

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

Сложение и вычитание комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 выполняется по правилам сложения и вычитания двучленов (многочленов) x1 + i y1 и x2 + i y2, например, по формулам

z1 + z2 =
= х1 + я у1 + х2 + я у2 =
= х1 + х2 + я (у1 + у2) ,

z1 — z2 =
= x1 + i y1– (x2 + i y2) =
= x1– x2 + i (y1– y2) .

Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2, а также операции сложения и вычитания производятся по правилам умножения двучленов (многочленов), однако учитывается важнейшее равенство, который имеет вид: я 2 = — 1 .

По этой причине

z1z2 = (x1 + я y1) (x2 + я y2) =
= x1x2 + я x1 y2 +
+ я y1x2 + я 2y1 y2 =
= x1x2 + я x1y2 +
+ я y1x2 — y1 y2 =
= x1x2 — y1 y2 +
+ я (х1 у2 + я х2 у1) .

Определения[]

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z2+1{\displaystyle z^{2}+1} имеет корень.
Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно.
Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел R{\displaystyle \mathbb {R} }, как и любые другие конструкции поля разложения многочлена x2+1{\displaystyle x^{2}+1}.

Стандартная модель

Формально, комплексное число z{\displaystyle z} — это упорядоченная пара вещественных чисел (x,y){\displaystyle (x,y)} с введёнными на них следующим образом операциями сложения и умножения:

• (x,y)+(x′,y′)=(x+x′,y+y′){\displaystyle (x,y)+(x’,y’)=(x+x’,y+y’)\,}
• (x,y)⋅(x′,y′)=(xx′−yy′,xy′+yx′).{\displaystyle (x,y)\cdot (x’,y’)=(xx’-yy’,xy’+yx’).\,}

Вещественные числа представлены в этой модели парами вида (x,){\displaystyle (x,0)}, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Мнимая единица в такой системе представляется парой i=(,1){\displaystyle i=(0,1)\,}.

Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа и при этом сохранив обычные свойства порядка, невозможно.

Матричная модель

Комплексные числа можно также определить как семейство вещественных матриц вида

(xy−yx){\displaystyle {\begin{pmatrix}x&y\\-y&\;\;x\end{pmatrix}}}

с обычным матричным сложением и умножением.
Действительной единице будет соответствовать

(11){\displaystyle {\begin{pmatrix}1&0\\0&\;\;1\end{pmatrix}}}

, мнимой единице —

(1−1){\displaystyle {\begin{pmatrix}0&1\\-1&\;\;0\end{pmatrix}}}

Замечания

• Ошибочно определение числа i{\displaystyle i} как единственного числа, удовлетворяющего уравнению i2=−1{\displaystyle i^{2}=-1}, так как число (−i){\displaystyle (-i)} также удовлетворяет этому уравнению.
• Следует также заметить, что часто используемое выражение i=−1{\displaystyle i={\sqrt {-1}}} не вполне корректно, так как алгебраический корень определяется над множеством неотрицательных чисел.

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

• целые числа;
• дроби;
• иррациональные числа.

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. z = a + bi

z = a + bi

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

• a — действительная часть (Re z) комплексного числа z;
• b — мнимая часть (Im z) комплексного числа z.

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

z = bi + a

Мнимую единицу допускается переставлять:

z = a + ib

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

z = a + bi

Определение

Комплексным числом называют выражение a + bi, в котором а и b являются действительными числами, i представляет собой мнимую единицу, символ, квадрат которого равен -1, то есть i2=-1. Число а представляет собой действительную часть, b — мнимую часть комплексного числа z = a + bi. Если b = 0, то вместо a + 0i записывают a. Действительные числа являются частным случаем комплексных чисел.

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

• ноль;
• единицу для действительной оси;
• мнимую единицу i для мнимо оси.

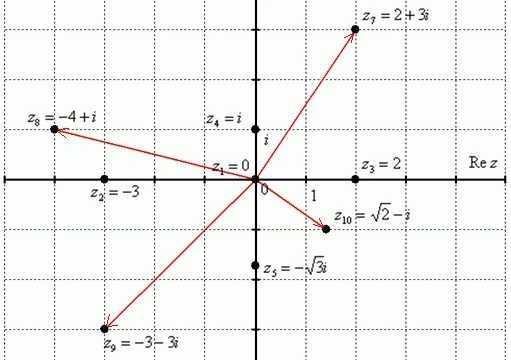
С помощью комплексной плоскости можно построить заданные комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Можно рассмотреть следующие комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

Есть ряд чисел с ненулевыми действительной и мнимой частью:

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Геометрическая интерпретация комплексных чисел

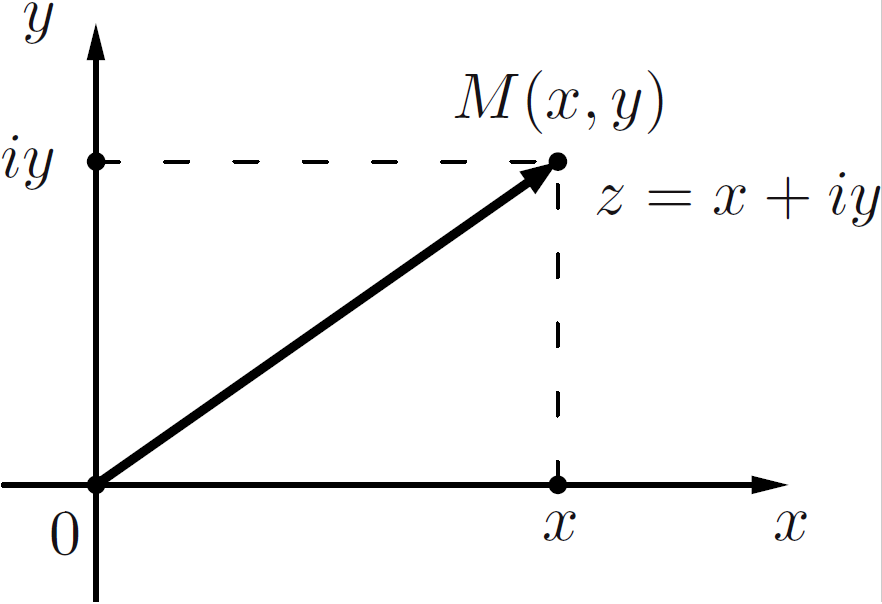
В 1799 году датчанин Каспар Вессель определил комплексное число как упорядоченную пару вещественных чисел $(x,y)$. Известно, что на декартовой
плоскости упорядоченной паре соответствует точка. Выберем на плоскости прямоугольную систему координат и установим взаимно однозначное
соответствие между комплексными числами и точками плоскости, при котором комплексному числу $z=x+\mathbf i y$ отвечает точка $M$ с координатами
$x,y$. Точку $M$ мы рассматриваем как изображение комплексного числа $z=x+\mathbf i y$.

При этом множество всех вещественных чисел изображается осью абсцисс, называемой поэтому вещественной осью, множество всех чисто мнимых
чисел лежит на оси ординат, называемой мнимой осью. Плоскость $XOY$, точки которой изображают комплексные числа, называется комплексной плоскостью (иногда гауссовой плоскостью) или просто плоскостью $z$. Термины «комплексное число $z$» и «точка $z$ на комплексной плоскости» употребляются как синонимы.

Комплексное число $z=x+\mathbf i y$ может также изображаться вектором с проекциями $x$ и $y$ на координатные оси, который, таким образом, равен
радиус-вектору точки $z$. Иногда термины «комплексное число» и «вектор» употребляют также как синонимы.

Именно поэтому, глядя на координатную плоскость,
естественно сделать вывод, что комплексные числа невозможно сравнивать, т.е. нельзя говорить, что какое-то комплексное число больше или меньше другого.

Комплексное число равное сумме или разности двух комплексных чисел $z_1\pm z_2$ соответствует вектору на комплексной плоскости, который получится при сложении/вычитании векторов, соответствующих числам $z_1$ и $z_2$. Для произведения $z_1\cdot z_2$ этой аналогии уже не будет.

Напомним, что в полярных координатах точка $M$ имеет координаты $(r,\varphi)$. В нашем случае полярные координаты имеют следующий смысл:

полярный радиус (или длина вектора) называется модулем комплексного числа $z=x+\mathbf i y$ и вычисляется по формуле

$$
r=|z|=\sqrt{x^2+y^2}=\sqrt{z\bar z},
$$

полярный угол $\varphi$ (угол между положительным направлением оси $OX$ и отрезком $OM$) называется аргументом комплексного числа $z$ и обозначается $\varphi=\mbox{Arg }z$.

Модуль и аргумент — две важнейшие характеристики комплексного числа.

Условия равенства двух комплексных чисел $z_1$ и $z_2$ — равенство их модулей: $|z_1|=|z_2|$ и аргументов: $\mbox{Arg }z_1=\mbox{Arg }z_2$.

Особый разговор об аргументе

Угол $\varphi=\mbox{Arg }z$ — аргумент комплексного числа $z=x+\mathbf i y$. Этот угол, изменяясь от положительного направления оси $OX$ против часовой
стрелки, увеличивается до $2\pi$, а далее его величины повторяются. Поэтому аргумент комплексного числа бесконечнозначен, так как все его
значения отличаются друг от друга на слагаемые, кратные $2\pi$.

Аргумент $\varphi$ определяется из формул
\begin{equation}
\left\{\begin{array}{l}
x=r\cos\varphi, \\
y=r\sin\varphi
\end{array}\right.
\end{equation}
с точностью до слагаемого $2\pi k$: $$
\mbox{Arg }z=\mbox{arg }z+2\pi k,\quad k=0,\pm1,\pm2,\ldots\ .
$$

Из множества значений аргумента особо выделяется главное значение $\mbox{arg }z$, удовлетворяющее неравенству $-\pi<\mbox{arg } z\le\pi$. При этом полезны
формулы
\begin{equation}
\arg z=\left\{\begin{array}{ll}
\mbox{arctg }\dfrac{y}{x},&x>0, \\
\mbox{arctg }\dfrac{y}{x}+\pi,&x<0,\ y\ge0, \\
\mbox{arctg }\dfrac{y}{x}-\pi,&x<0,\ y<0.\\
\end{array}\right.
\end{equation}

Для комплексного числа $z=0+\mathbf i 0$ понятие аргумента не
имеет смысла.

Условие сопряжения двух чисел $z$ и $\bar{z}$:
$$|z|=|\bar{z}|,\quad \arg z=-\arg \bar{z}.$$

Некоторые свойства модуля:
$$
\left| z_1 + z_2 \right| \le \left| z_1\right| + \left| z_2\right| \ ,
$$
$$
\left| z_1 + z_2 \right| \ge \big| | z_1 | — | z_2 | \big| \ ,
$$
$$
\left| z_1 — z_2 \right| \ge \big| | z_1 | — | z_2 | \big|.
$$

Ссылки[]

• Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов, МЦНМО, 2002
• Елисеев В. И. «Введение в методы теории функций пространственного комплексного переменного», Центр научно-технического творчества молодежи Алгоритм. — М.:, НИАТ. — 1990. Шифр Д7-90/83308
• Понтрягин Л. Комплексные числа, Квант, № 3, 1982.
• Простой калькулятор комплексных чисел
• CaRevol Jet — Формульный калькулятор комплексных чисел под Windows.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 2001. — Т. II. — 680 с. — ISBN 5-9221-0156-0, 5-9221-0155-2, 5-9221-0436-5

Действия над комплексными числами[]

• Сравнение

  a+bi=c+di{\displaystyle a+bi=c+di} означает, что a=c{\displaystyle a=c} и b=d{\displaystyle b=d}.

• Сложение

  (a+bi)+(c+di)=(a+c)+(b+d)i{\displaystyle (a+bi)+(c+di)=(a+c)+(b+d)i}

• Вычитание

  (a+bi)−(c+di)=(a−c)+(b−d)i{\displaystyle (a+bi)-(c+di)=(a-c)+(b-d)i}

• Умножение

  (a+bi)(c+di)=ac+bci+adi+bdi2=(ac−bd)+(bc+ad)i{\displaystyle (a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i}

• Деление

  (a+bi)(c+di)=(ac+bdc2+d2)+(bc−adc2+d2)i{\displaystyle \,{\frac {(a+bi)}{(c+di)}}=\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i\,}

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что