Сложение и вычитание комплексных чисел

Свойство операции умножения

Операция умножения обладает следующим неочевидным свойством.

Это означает, что при перемножении двух чисел их аргументы (углы) складываются, а длина умножается.

Посмотрите еще раз внимательно на умножение. Я специально пометил вершины, чтобы было видно, что при умножении вершины действительно складываются.

Допустим, у нас есть число X. Когда мы умножаем его на другое число Y, мы, таким образом, расширяем число X до |Y| раз и повернуть на угол Arg(Y).

Кстати, операции поворота и растяжения коммутируют друг с другом

Им неважно, в каком порядке мы их выполняем. Они как бы бегут одновременно

Геометрическая интерпретация комплексных чисел

В 1799 году датчанин Каспар Вессель определил комплексное число как упорядоченную пару вещественных чисел $(x,y)$. Известно, что на декартовой
плоскости упорядоченной паре соответствует точка. Выберем на плоскости прямоугольную систему координат и установим взаимно однозначное
соответствие между комплексными числами и точками плоскости, при котором комплексному числу $z=x+\mathbf i y$ отвечает точка $M$ с координатами
$x,y$. Точку $M$ мы рассматриваем как изображение комплексного числа $z=x+\mathbf i y$.

При этом множество всех вещественных чисел изображается осью абсцисс, называемой поэтому вещественной осью, множество всех чисто мнимых
чисел лежит на оси ординат, называемой мнимой осью. Плоскость $XOY$, точки которой изображают комплексные числа, называется комплексной плоскостью (иногда гауссовой плоскостью) или просто плоскостью $z$. Термины «комплексное число $z$» и «точка $z$ на комплексной плоскости» употребляются как синонимы.

Комплексное число $z=x+\mathbf i y$ может также изображаться вектором с проекциями $x$ и $y$ на координатные оси, который, таким образом, равен
радиус-вектору точки $z$. Иногда термины «комплексное число» и «вектор» употребляют также как синонимы.

Именно поэтому, глядя на координатную плоскость,
естественно сделать вывод, что комплексные числа невозможно сравнивать, т.е. нельзя говорить, что какое-то комплексное число больше или меньше другого.

Комплексное число равное сумме или разности двух комплексных чисел $z_1\pm z_2$ соответствует вектору на комплексной плоскости, который получится при сложении/вычитании векторов, соответствующих числам $z_1$ и $z_2$. Для произведения $z_1\cdot z_2$ этой аналогии уже не будет.

Напомним, что в полярных координатах точка $M$ имеет координаты $(r,\varphi)$. В нашем случае полярные координаты имеют следующий смысл:

полярный радиус (или длина вектора) называется модулем комплексного числа $z=x+\mathbf i y$ и вычисляется по формуле

$$
r=|z|=\sqrt{x^2+y^2}=\sqrt{z\bar z},
$$

полярный угол $\varphi$ (угол между положительным направлением оси $OX$ и отрезком $OM$) называется аргументом комплексного числа $z$ и обозначается $\varphi=\mbox{Arg }z$.

Модуль и аргумент — две важнейшие характеристики комплексного числа.

Условия равенства двух комплексных чисел $z_1$ и $z_2$ — равенство их модулей: $|z_1|=|z_2|$ и аргументов: $\mbox{Arg }z_1=\mbox{Arg }z_2$.

Особый разговор об аргументе

Угол $\varphi=\mbox{Arg }z$ — аргумент комплексного числа $z=x+\mathbf i y$. Этот угол, изменяясь от положительного направления оси $OX$ против часовой
стрелки, увеличивается до $2\pi$, а далее его величины повторяются. Поэтому аргумент комплексного числа бесконечнозначен, так как все его
значения отличаются друг от друга на слагаемые, кратные $2\pi$.

Аргумент $\varphi$ определяется из формул
\begin{equation}
\left\{\begin{array}{l}
x=r\cos\varphi, \\
y=r\sin\varphi
\end{array}\right.
\end{equation}
с точностью до слагаемого $2\pi k$: $$
\mbox{Arg }z=\mbox{arg }z+2\pi k,\quad k=0,\pm1,\pm2,\ldots\ .
$$

Из множества значений аргумента особо выделяется главное значение $\mbox{arg }z$, удовлетворяющее неравенству $-\pi<\mbox{arg } z\le\pi$. При этом полезны
формулы
\begin{equation}
\arg z=\left\{\begin{array}{ll}
\mbox{arctg }\dfrac{y}{x},&x>0, \\
\mbox{arctg }\dfrac{y}{x}+\pi,&x<0,\ y\ge0, \\
\mbox{arctg }\dfrac{y}{x}-\pi,&x<0,\ y<0.\\
\end{array}\right.
\end{equation}

Для комплексного числа $z=0+\mathbf i 0$ понятие аргумента не
имеет смысла.

Условие сопряжения двух чисел $z$ и $\bar{z}$:
$$|z|=|\bar{z}|,\quad \arg z=-\arg \bar{z}.$$

Некоторые свойства модуля:
$$
\left| z_1 + z_2 \right| \le \left| z_1\right| + \left| z_2\right| \ ,
$$
$$
\left| z_1 + z_2 \right| \ge \big| | z_1 | — | z_2 | \big| \ ,
$$
$$
\left| z_1 — z_2 \right| \ge \big| | z_1 | — | z_2 | \big|.
$$

§ 1. Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах

Определение комплексного числа (Сформулируйте определение комплексного числа)

Комплексным числомz называется выражение следующего вида:

Комплексное число в алгебраической форме,(1)

Где x, y

Î;

— комплексно сопряженное число
числу z

;

— противоположное число
числу z

;

— комплексный ноль
;

– так обозначается множество комплексных чисел.

1)z

= 1 + i

Þ Re z

= 1, Im z

= 1, = 1 – i,

= –1 – i

;

2)z

= –1 + i

Þ Re z

= –1, Im z

= , = –1 – i,

= –1 –i

;

3)z

= 5 + 0i

= 5 Þ Re z

= 5, Im z

= 0, = 5 – 0i

= 5, = –5 – 0i

= –5

Þ если Imz

= 0, то z

= x

— действительное число;

4)z

= 0 + 3i

= 3i

Þ Re z

= 0, Im z

= 3, = 0 – 3i

= –3i

, = –0 – 3i

= – 3i

Þ если Rez

= 0, то z

= iy

— чисто мнимое число
.

Комплексные равенства
(Сформулируйте смысл комплексного равенства)

1) ;

2) .

Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.

1) ;

2) .

Комплексное число z

изображается точкой (x

, y
) на комплексной плоскости или радиус-вектором этой точки.

Знак z

во второй четверти означает, что система декартовых координат будет использоваться как комплексная плоскость.

Модуль и аргумент комплексного числа
(Что такое модуль и аргумент комплексного числа?)

Модулем комплексного числа называется неотрицательное действительное число

.(2)

Геометрически модуль комплексного числа — это длина вектора, изображающего число z

, или полярный радиус точки (x

, y
).

Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.

1)z

= 1 + i

Þ

,

Þ

Þ;

,

Þ

Þ;

,

5),

то есть для z = 0 будет

, j

не определен.

Арифметические действия над комплексными числами
(Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.)

Сложение (вычитание) комплексных чисел

z

1 ±z

2 = (x

1 + iy

1) ± (x

2 + iy

2) = (x

1 ±x

2) + i

(y

1 ±y

2),(5)

то есть при сложении (вычитании) комплексных чисел складываются (вычитаются) их действительные и мнимые части.

1)(1 + i
) + (2 – 3i
) = 1 + i

+ 2 –3i

= 3 – 2i

;

2)(1 + 2i
) – (2 – 5i
) = 1 + 2i

– 2 + 5i

= –1 + 7i

.

1)z

1 + z

2 = z

2 + z

1;

2)z

1 + z

2 + z

3 = (z

1 + z

2) + z

3 = z

1 + (z

2 + z

3);

3)z

1 – z

2 = z

1 + (– z

2);

4)z

+ (–z
) = 0;

Умножение комплексных чисел в алгебраической форме

z

1∙z

2 = (x

1 + iy

1)∙(x

2 + iy

2) = x

1x

2 + x

1iy

2 + iy

1x

2 + i

2y

1y

2 = (6)

= (x

1x

2 – y

1y

2) + i

(x

1y

2 + y

1x

2),

то есть умножение комплексных чисел в алгебраической форме проводится по правилу алгебраического умножения двучлена на двучлен с последующей заменой и приведением подобных по действительным и мнимым слагаемым.

1)(1 + i
)∙(2 – 3i
) = 2 – 3i

+ 2i

– 3i

2 = 2 – 3i

+ 2i

+ 3 = 5 – i

;

2)(1 + 4i
)∙(1 – 4i
) = 1 – 42 i

2 = 1 + 16 = 17;

3)(2 + i
)2 = 22 + 4i

+ i

2 = 3 + 4i

.

Умножение комплексных чисел тригонометрической форме

z

1∙z

2 = r

1(cosj

1 + i

sinj

1)×r

2(cosj

2 + i

sinj

2) =

= r

1r

2(cosj

1cosj

2 + i

cosj

1sinj

2 + i

sinj

1cosj

2 + i

2 sinj

1sinj

2) =

= r

1r

2((cosj

1cosj

2 – sinj

1sinj

2) + i

(cosj

1sinj

2 + sinj

1cosj

2))

Произведение комплексных чисел в тригонометрической форме, то есть при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

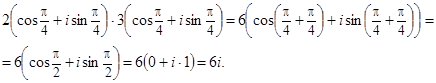
Основные свойства умножения

1)z

1×z

2 = z

2×z

1 — коммутативность;

2)z

1×z

2×z

3 = (z

1×z

2)×z

3 = z

1×(z

2×z

3) — ассоциативность;

3)z

1×(z

2 + z

3) = z

1×z

2 + z

1×z

3 — дистрибутивность относительно сложения;

4)z

×0 = 0; z

×1 = z

;

Деление комплексных чисел

Деление — это обратная умножению операция, поэтому

если z

×z

2 = z

1 и z

2 ¹ 0, то .

При выполнении деления в алгебраической форме числитель и знаменатель дроби умножаются на число, комплексно сопряженное знаменателю:

Деление комплексных чисел в алгебраической форме.(7)

При выполнении деления в тригонометрической форме модули делятся, а аргументы вычитаются:

Деление комплексных чисел в тригонометрической форме.(8)

2).

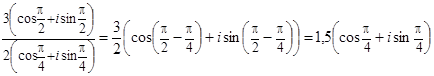Возведение комплексного числа в натуральную степень

Возведение в натуральную степень удобнее выполнять в тригонометрической форме:

Формула Муавра,(9)

то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.

Вычислить (1 + i
)10.

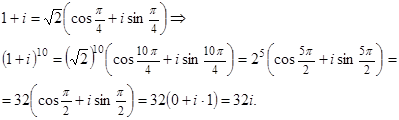
Замечания

1. При выполнении операций умножения и возведения в натуральную степень в тригонометрической форме могут получаться значения углов за пределами одного полного оборота. Но их всегда можно свести к углам или сбрасыванием целого числа полных оборотов по свойствам периодичности функций и .

2. Значение называют главным значением аргумента комплексного числа ;

при этом значения всех возможных углов обозначают ;

очевидно, что , .

Извлечение корня натуральной степени из комплексного числа

Формулы Эйлера(16)

по которым тригонометрические функции и действительной переменной выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.

Геометрическая интерпретация комплексных чисел

Итак, комплексное число — это просто конструкция вида $a+bi$. И такая конструкция однозначно определяется парой действительных чисел $\left( a;b \right)$. Такую пару ещё называют упорядоченной. К примеру, (3; 17) и (17; 3) — это разные пары, которые задают разные комплексные числа.

Такие упорядоченные пары удобно рассматривать как координаты точек. По горизонтали (ось абсцисс) мы будем отмечать действительную часть числа, а по вертикали (ось ординат) — мнимую.

Рассмотрим несколько примеров. Отметим на комплексной плоскости числа:

\

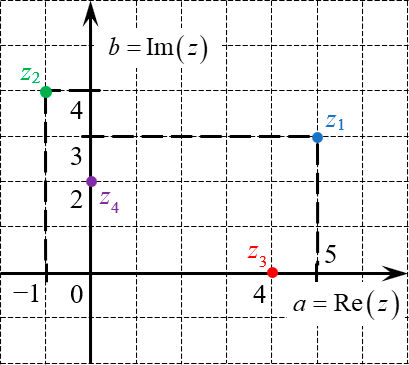
Как видим, привычные нам действительные числа располагаются по горизонтали — на оси абсцисс. Они состоят только из действительной части. Таким числом является ${{z}_{3}}=4+0\cdot i$ (отмечено красным).

А ещё есть «чисто мнимые» комплексные числа, у которых вообще нет действительной части. Они располагаются по вертикали — на оси ординат. Таким числом является, например, ${{z}_{4}}=0+2i$ (отмечено фиолетовым).

4.1. Ещё раз о сложении и вычитании

Такое представление чисел — в виде точек на комплексной плоскости — называется геометрической интерпретацией. Числа в таком виде удобно складывать и вычитать. По сути, всё сводится к сложению обычных векторов.

Допустим, мы хотим сложить два числа:

\

Отметим эти числа на комплексной плоскости, построим векторы из начала координат с концами в отмеченных точках, а затем просто сложим эти векторы (по правилу треугольника или параллелограмма — как пожелаете):

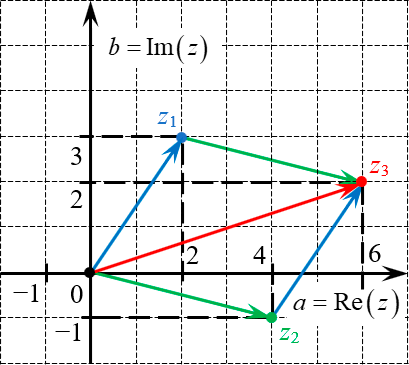
Координаты новой точки: (6; 2). Следовательно, сумма равна:

\

Аналогичный результат можно получить и алгебраически:

\

Как видим, алгебраические выкладки заняли гораздо меньше времени и места. Уже хотя бы потому что не потребовалось чертить систему координат.:)

Зачем же тогда нужна комплексная плоскость и геометрическая интерпретация? Всё встанет на свои места буквально через пару уроков, когда мы рассмотрим тригонометрическую форму записи комплексных чисел, а также будем извлекать из этих чисел корни.

А чтобы подготовиться к этим урокам, рассмотрим ещё два ключевых определения.

Тригонометрическая форма записи комплексного числа

Приведенную выше информацию можно назвать «комплексные числа для чайников». Она включила информацию про комплексные числа кратко представленную в доступной для читателя форме.

Если же есть необходимость углубляться в теорию комплексных чисел, то тут уже стоит рассматривать тригонометрическую форму записи комплексного числа. Она представляет собой выражение вида r * (cos(f) + i * sin(f)).

В представленном выражении появляются новые обозначения помимо хорошо известных тригонометрических функций косинус и синус, которые находятся от угла f.

Итак, именно с угла f и начнем пояснение. Величина f для комплексного числа это угол наклона вектора, который характеризует комплексное число. Рассмотренная величина называется аргументом комплексного числа и используется не только в тригонометрической, а и в показательной форме записи комплексных чисел. Она может принимать как положительные, так и отрицательные значения.

Теперь вернемся к первому множителю, который указан в тригонометрической форме записи – множитель r. Эта величина r называется модулем комплексного числа. Для его вычисления необходимо найти корень квадратный из суммы квадратов действительной и мнимой частей комплексного числа. При извлечении корня, находят арифметический квадратный корень, поэтому полученное значение величины r всегда будет только положительным (больше нуля).

Тригонометрическая, как и показательная формы записи комплексного числа необходимы в первую очередь для проведения таких операций над комплексными числами как извлечения корня комплексного числа, а также возведения комплексного числа в любую степень.

Безусловно, если говорить про алгебраическую форму записи, то возведение в степень будет доступным, но уже при возведении в степень большую чем, например, третья, будут возникать неудобства вычисления.

Возводя же в любую степень комплексное число в тригонометрической форме, достаточно в эту степень возвести модуль комплексного числа, а его аргумент – умножить на указанный показатель степени. В случае получения достаточно больших значений для аргумента, их без труда можно уменьшить, используя периодичность тригонометрических функций синус и косинус.

При правильном подходе видим, что комплексные числа являются достаточно простой темой, а действия над ними схожи с теми действиями, которые выполнялись при изучении таких тем курса алгебры и начал анализа как:

• Тригонометрические функции;
• Степенные выражения и действия над ними;
• Многочлены и действия над ними.

Расширенная комплексная плоскость. Сфера Римана

Из геометрии известно, что любой упорядоченной паре вещественных чисел соответствует точка $z$ на плоскости комплексного переменного. Определим
на комплексной плоскости бесконечно удаленную точку. Так условно будем называть «мысленную точку» $(x,y)$, координаты которой (обе сразу
или одна из них) — величины неограниченные, т.е. комплексные числа имеют формальный вид $z=x+i\infty$, $z=\infty+iy$ либо $z=\infty+i\infty$.
Тогда пишут $z=\infty$ (несобственное комплексное число), считая ее единственной бесконечно удаленной точкой.

Для несобственного комплексного числа понятия вещественной и мнимой части, а также понятие аргумента не вводятся; точнее говоря, объявляются
лишенными смысла (напомним, что понятие аргумента не имеет смысла и для числа 0). Что касается модуля числа $z=\infty$, то для него используется
символ $|\infty|=+\infty$.

Договорились, что имеют смысл следующие операции, в которых участвуют $z=\infty$ и собственное комплексное число $a$: $$
\frac{a}\infty=0,\quad\frac\infty{a}=\infty,\quad\frac{a}0=\infty.
$$ Такие операции, как $$
\infty\pm\infty,\quad 0\cdot\infty,\quad \dfrac00,\quad
\dfrac\infty\infty
$$ объявляются лишенными смысла.

Совокупность точек комплексной плоскости и бесконечно удаленной точки называется расширенной плоскостью комплексного переменного.

Наглядное представление о расширенной комплексной плоскости дает следующая интерпретация Римана (1826-1866).

Чтобы получить геометрическое изображение числа $\infty$, прибегают к представлению комплексных чисел точками сферы. Построим сферу (называемую сферой Римана) радиуса $r$, касающуюся плоскости $z$ в точке $z=0$ и отметим точку $N$ сферы, диаметрально противоположную началу
координат $O$.

Из точки $N(0,0,2r)$ сферы проведем проведем луч в любую точку $Z(x,y,0)$ плоскости $(x,y)$ и отметим точку $S$ пересечения данного луча и
сферы. Эта точка $S(\xi,\eta,\zeta)$ является новым геометрическим представлением комплексного числа $z$. В результате таких
построений лучей между точками плоскости $(x,y)$ и точками сферы устанавливается взаимно однозначное соответствие, называемое стереографической
проекцией, имеющей применение в картографии.

Точкам меридиана $NSO$ на сфере соответствуют точки луча $OZ$ на плоскости $(x,y)$, различным параллелям — круги на плоскости $(x,y)$.
Исключение составляет точка $N$. Северному полюсу $N$ сферы не соответствует пока никакое комплексное число. Однако точкам сферы, достаточно
близким к $N$, соответствуют точки $z$ плоскости, сколь угодно далеко отстоящие от начала координат, т.е. точка $z$ сколь угодно большого
модуля. Будем считать, что точке $N$ соответствует единственная точка $z=\infty$.

Покажем, что точка $z=\infty+\mathbf i \infty$ (или $z=x+\mathbf i \infty$, или $z=\infty+\mathbf i y$) будет при таком преобразовании переходить в точку $N(0,0,2r)$ и
наоборот. Координаты точек на такой сфере $(\xi,\eta,\zeta)$ связаны формулой
\begin{equation}\label{eq g1 p7 1}
\xi^2+\eta^2+(\zeta-r)^2=r^2\quad\hbox{или}\quad \xi^2+\eta^2=\zeta
(2r-\zeta).
\end{equation}

Из коллинеарности $NZ$ и $NS$ можно получить представление луча $NSZ$
$$
\frac{\xi-0}{x-0}=\frac{\eta-0}{y-0}=\frac{\zeta-2r}{0-2r}.
$$
Отсюда можно получить координаты точек плоскости через координаты точек сферы:
\begin{equation}\label{eq g1 p7 2}
x=\frac{2r\xi}{2r-\zeta},\quad y=\frac{2r\eta}{2r-\zeta}.
\end{equation}

Составим
$$ x^2+y^2=\frac{4r^2(\xi^2+\eta^2)}{(2r-\zeta)^2}, $$
$$ x^2+y^2 = \frac{4r^2\zeta}{2r-\zeta}. $$
Тогда
можно выразить координату
$$
\zeta=\frac{2r(x^2+y^2)}{x^2+y^2+4r^2},
$$
и другие координаты
$$
\xi=\frac{4r^2x}{x^2+y^2+4r^2},\quad\eta=\frac{4r^2y}{x^2+y^2+4r^2}.
$$

Устремим $x\to\infty$, $y\to\infty$ (по отдельности или вместе), тогда $\xi\to0$, $\eta\to0$, $\zeta\to2r$, а это и есть точка $N$.

Некоторые сведения о комплексных числах подробнее изложены в курсе Высшей алгебры А.Ю. Утешева ( здесь).

Модуль и Аргумент комплексного числа

Если рассматривать комплексное число как вектор, то можно найти его модуль, т.е длину вектора. Для этого воспользуемся обычной теоремой Пифагора.

модуль комплексного числа Модуль комплексного числа

Мы также можем определить так называемый аргумент для комплексных чисел. Аргументом является угол между положительным направлением действительной оси и вектором.

Если комплексное число расположено в верхней полуплоскости, аргумент считается положительным, в противном случае — отрицательным. Таким образом, аргумент принимает значения от -Пи до Пи радиан (или от -180 до 180 градусов).

По сути, модуль и аргумент — это просто еще одно представление комплексного числа. Это его полярные координаты. Если мы знаем модуль и аргумент, то это число определяет само себя.

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

Действительно, умножение и деление двух произвольных комплексных чисел

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле

Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Алгебраические формы комплексного числа

Определение

Алгебраические формы комплексного числа – это комплексное число в виде , где и  – действительные числа; число  называется действительной, а – мнимой частью комплексного числа.

Обозначения: ; символ формально определяется равенством называется мнимой единицей.

Два комплексных числа называются равными, если в соответствии равные их действительные и мнимые числа.

Ниже будут рассмотрены более подробно основные операции над комплексными числами в алгебраической форме.

Дальше договоримся выражения и т. д. считать комплексными числами, записанными в алгебраической форме, значит,   и т. п. приобретаются только действительные значения.

Пусть дано число . Если , тогда – действительное число: ; если тогда – это мнимое число:

;

.

Допустим:

.

Умножение комплексных чисел выполняется согласно правилу (считая, что ):

.

Деление комплексных чисел согласно правилу (при условии .

= = = = = .

Сопряженные комплексные числа

Сопряженные числа – это числа и . Таким образом, если и сопряженные числа, тогда и .

Очевидно, если – действительное число, тогда ; если – чисто мнимое число, тогда . Наоборот, если  и , тогда соответственно и – действительные и чисто мнимые числа.

Модуль комплексного числа

Модуль числа называется число .

Модуль действительного числа равняется его абсолютной величине. Правда, если , тогда .

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Тригонометрическая и показательная форма комплексных чисел

Сложение и вычитание комплексных чисел в алгебраической форме

Складывать и вычитать комплексные числа в алгебраической форме очень просто. В случае сложения просто сложите действительные составляющие комплексных чисел, чтобы определить действительную составляющую суммы, и сложите мнимые составляющие комплексных чисел, чтобы определить мнимую составляющую суммы:

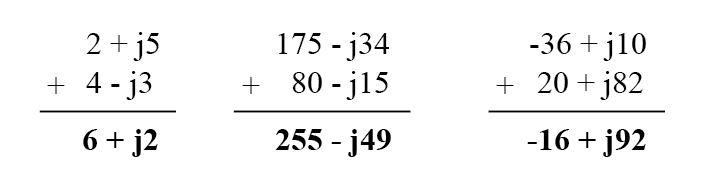Рисунок 1 – Сложение комплексных чисел в алгебраической форме

При вычитании комплексных чисел в алгебраической форме просто вычтите действительную составляющую второго комплексного числа из действительной составляющей первого, чтобы получить действительную составляющую разности, и вычтите мнимую составляющую второго комплексного числа из мнимой составляющей первого числа, чтобы получить мнимую составляющую разности:

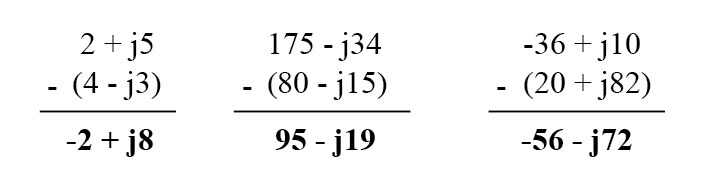Рисунок 2 – Вычитание комплексных чисел в алгебраической форме

Понятие комплексного числа

Комплексные числа – это мнимые числа или выражение такого вида, как , где и – действительные числа (ещё про них говорят вещественные числа), а – это мнимая единица, символ, квадрат которого равен 1 . Число – действительная часть, – мнимая часть комплексного числа . Если тогда вместо пишется просто . Из вышесказанного понятно, что действительные числа – частный случай комплексных чисел.

С комплексными числами можно проводить разные арифметические действия: сложение, вычитание, умножение и деление.

Рассмотрим уравнение . Его можно отнести к возведённому квадратному уравнению ., корни которого находятся по формуле .

Для данного случая получается:

.

Среди действительных чисел выражение не имеет смысла, то есть  не есть действительным числом. Запишем формально .

Символ принято обозначать буквой , то есть . Его называют мнимой единицей.

Корни нашего уравнения теперь запишутся:

.

Проверка:

Для имеем:

.

Аналогично для .

Значит, введение символа , где помогает нам записывать выражение для корней квадратного уравнения и тогда, когда дискриминант отрицательный.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что