Модуль числа

Геометрическая интерпретация и графическое решение задачи линейного программирования

Геометрическая интерпретация задач дает возможность наглядно представить их структуру, выявить особенности. Задачу линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно.

Рассмотрим случай двух переменных:

Дадим геометрическую интерпретацию элементов этой задачи.

Каждое из ограничений (6), (7) задаёт на плоскости x₁Ox₂ некоторую полуплоскость. Полуплоскость – выпуклое множество. Напомним, что выпуклым называют множество, которое вместе с любыми своими точками x₁и x₂содержит и все точки отрезка [ x₁; x₂]. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений (ОДР) задачи есть выпуклое множество.

Возможны ситуации, когда область допустимых решений ЗЛП:

— неограниченная выпуклая многоугольная область;

Геометрическая интерпретация целевой функции.

Пусть ОДР задачи ЛП – непустое множество.

Выберем произвольное значение целевой функции

x₁x₂:

Частная производная функции показывает скорость её возрастания вдоль данной оси. с₁и с₂– скорости возрастания

Ox₁Ox₂
градиентом функции

Вектор

Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения.

1. С учетом системы ограничений строится область допустимых решений.

2. Строится вектор

3. Проводится произвольная линия, перпендикулярная к вектору

4. При решении задачи на максимум перемещается линия уровня в направлении вектора

В случае задачи на минимум линия уровня перемещается в антиградиентном направлении.

5. Определяется оптимальный план

Возможны следующие случаи:

— оптимальный план единственный;

— оптимальных планов бесконечное множество: в разрешающем положении линия уровня проходит через сторону области допустимых решений;

— целевая функция неограниченна;

— область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального и минимального значения;

— задача не имеет решения: ОДР – пустое множество, т.е. система ограничений задачи несовместна.

Пример. Пусть предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами 3-х видов С, D и E в объёмах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и даны в таблице 1. Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В- 50 млн. руб. Требуется найти объёмы производства изделий, обеспечивающие максимальную прибыль.

Свойства модуля (абсолютной величины)

Точка O на координатной прямой — это точка, из которой шар покатился — начальная точка.

Один отрезок прямой линии равен 1 делению — 1 метру.

Точка A на координатной прямой A (+ 3 ) — это момент удара мяча о стену.

Точка B с координатой B ( 0 ) — совпадает с начальной точкой.

Можно ли сказать, что мяч не прошел никакого расстояния, пока покоился в начале координат, потому что он приземлился в точке 0 м (ни один единичный отрезок не подходит от точки 0 до начала координат O)? Конечно, нет!

Шарик прошел бы путь, равный нулю, если бы его вообще не толкали и он оставался бы в состоянии покоя в точке O.

Однако следует учитывать, что путь (расстояние), пройденный мячом, состоит из 3 единичных отрезков справа и 3 единичных отрезков слева; если мы все

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Проблема 1.

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Решение:

Проведем координатную линию с началом координат в точке O.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна для зарегистрированных пользователей

Мы знаем, что мерой числа является расстояние (количество единичных отрезков) от нуля до данной точки.

Мы можем отложить 142 единичных отрезка вправо на координатной прямой и получить точку с координатами 142.

Мы также можем отложить 142 единичных отрезка влево от нуля и получить точку с координатами 142.

На координатной прямой есть два числа, которые по модулю равны 142, и расстояние между этими точками содержит по 142 единичных отрезка.

|142| = 142

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите числа — 15 ; — 1 ; — 1 ? 4 ; 7 в порядке возрастания по модулю.

Использование модуля в реальной жизни

Модуль, как математическое понятие, находит применение в реальной жизни во многих областях. Например, в физике при расчете силы тяжести для объектов находящихся на определенной высоте, а также при определении скорости движения тел.

Также модуль используется в астрономии при определении размеров планет и космических объектов по их орбитам и расстояниям между ними.

В области экономики и финансов модуль находит применение при расчетах процентных ставок и прибыли по кредитам и вкладам, а также при оценке рисков в инвестиционной деятельности.

Все эти примеры показывают, что понимание модуля как математического понятия является невероятно важным в реальной жизни. Умение использовать модуль для решения задач может помочь во многих жизненных ситуациях и в разных сферах деятельности.

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке  величина будет отрицательной, а на интервале  будет положительной.

Разделим интервал на 2 части:

1. для x + 2 ≥ 0

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

1. для х + 2 &lt, 0

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

x ∈ (–∞, –3] ∪ [–1, + ∞).

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

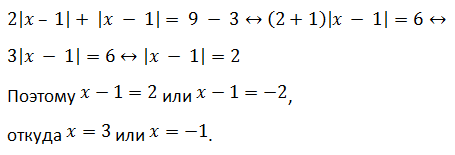
Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

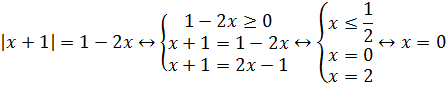
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что  не лежит в промежутке. Ответ: x = 0

Ответ: x = 0.

Модуль комплексного числа

Дадим определение модуля комплексного числа
. Пусть нам дано комплексное число
, записанное в алгебраической форме , где x
и y
– некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z
, а – мнимая единица.

Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль
:

• если значение выражения больше нуля, то просто выносим его из-под знака модуля,
• если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.

Ну что, попробуем? Оценим:

(Забыл, Повтори.)

Если, то какой знак имеет? Ну конечно, !

А, значит, знак модуля раскрываем, меняя знак у выражения:

Разобрался? Тогда попробуй сам:

Ответы:

Какими же ещё свойствами обладает модуль?

Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.

Например:

А что, если нам нужно разделить два числа (выражения) под знаком модуля?

Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:

при условии, что (так как на ноль делить нельзя).

Стоит запомнить ещё одно свойство модуля:

Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:

Почему так? Всё очень просто!

Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное. Допустим, что числа и оба положительные. Тогда левое выражение будет равно правому выражению.

Рассмотрим на примере:

Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:

Вроде с этим свойством все ясно, рассмотрим еще парочку полезных свойств модуля.

Что если перед нами такое выражение:

Что мы можем сделать с этим выражением? Значение x нам неизвестно, но зато мы уже знаем, что, а значит.

Число больше нуля, а значит можно просто записать:

Вот мы и пришли к другому свойству, которое в общем виде можно представить так:

А чему равно такое выражение:

Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?

Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему . И что же получается? А вот что:

Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:

Ну, и почему сомнения? Действуем смело!

Во всем разобрался? Тогда вперед тренироваться на примерах!

1. Найдите значение выражения, если.

2. У каких чисел модуль равен?

3. Найдите значение выражений:

Если не все пока ясно и есть затруднения в решениях, то давай разбираться:

Решение 1
:

Итак, подставим значения и в выражение

Решение 2:

Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное имеют два числа: и.

Решение 3:

а)
б)
в)
г)

Все уловил? Тогда пора перейти к более сложному!

Попробуем упростить выражение

Решение:

Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное
, то мы просто можем отбросить знак: модуль числа будет равен этому числу.

Но если под знаком модуля отрицательное число
, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «-»).

Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.

Получается, значение первого выражения под модулем.

Следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.

Итак, значение первого выражения под знаком модуля отрицательно, второго — положительно:

Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «-». Вот так:

Во втором случае просто отбросим знак модуля:

Упростим данное выражение целиком:

Докажите свойство модуля: \( \left| x+y \right|\le \left| x \right|+\left| y \right|\)

Доказательство

Предположим, что существуют такие \( x;y\in \mathbb{R}\), что \( \left| x+y \right|>\left| x \right|+\left| y \right|.\) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):

\( \displaystyle \begin{array}{l}\left| x+y \right|>\left| x \right|+\left| y \right|\Leftrightarrow \\{{\left( x+y \right)}^{2}}>{{\left( \left| x \right|+\left| y \right| \right)}^{2}}\Leftrightarrow \\{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2\cdot \left| x \right|\cdot \left| y \right|+{{y}^{2}}\Leftrightarrow \\xy>\left| x \right|\cdot \left| y \right|\Leftrightarrow \\xy>\left| xy \right|,\end{array}\)а это противоречит определению модуля.

Следовательно, таких \( x;y\in \mathbb{R}\) не существует, а значит, при всех \( x,\text{ }y\in \mathbb{R}\) выполняется неравенство \( \left| x+y \right|\le \left| x \right|+\left| y \right|.\)

Что такое модуль действительного числа: определение, примеры, график, интерпретация

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Что такое модуль действительного числа

В данной публикации мы рассмотрим определение, геометрическую интерпретацию, график функции и примеры модуля положительного/отрицательного числа и нуля.

• Определение модуля числа
• Геометрическая интерпретация модуля
• График функции с модулем
• Пример задачи

Определение модуля числа

Модуль действительного числа (иногда называется абсолютной величиной) – это величина, равная ему же, если число положительное или равная противоположному, если оно отрицательное.

Модуль числа a обозначается вертикальными черточками с обеих сторон от него – |a|.

Противоположное число отличается от исходного знаком. Например, для числа 5 противоположным является -5. При этом ноль является противоположным самому себе, т.е. |0| = 0.

Геометрическая интерпретация модуля

Модуль числа a – это расстояние от начала координат (O) до точки A на координатной оси, которая соответствует числу a, т.е. |a| = OA.

|-4| = |4| = 4

График функции с модулем

График четной функции y = |х| выглядит следующим образом:

• y = x при x>0
• y = -x при x<0
• y=0 при x=0
• область определения: (−∞;+∞)
• область значений: [0;+∞).
• в точке x=0 график “ломается”.

Пример задачи

Чему равняются следующие модули |3|, |-7|, |12,4| и |-0,87|.

Решение:Согласно приведенному выше определению:

• |3| = 3
• |-7| = 7
• |12,4| = 12,4
• |-0,87| = 0,87

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

1. Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
2. Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
3. Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
4. Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
5. Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
6. Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
7. Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
8. Такое же правило распространяется и на показатель степени выражения.

Свойства модуля

Модулю присущ ряд характерных результатов — свойства модуля
. Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом
. В буквенном виде это свойство имеет запись вида для любого числа a
. Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль
. Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O
, не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a
. Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел
, то есть, . По определению модуль произведения чисел a
и b
равен либо a·b
, если , либо −(a·b)
, если . Из правил умножения действительных чисел следует, что произведение модулей чисел a
и b
равно либо a·b
, , либо −(a·b)
, если , что доказывает рассматриваемое свойство.

Модуль частного от деления a
на b
равен частному от деления модуля числа a
на модуль числа b

, то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

Следующее свойство модуля записывается в виде неравенства: , a
, b
и c
– произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника
. Чтобы это стало понятно, возьмем точки A(a)
, B(b)
, C(c)
на координатной прямой, и рассмотрим вырожденный треугольник АВС
, у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ
, — длине отрезка АС
, а — длине отрезка СВ
. Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел
». Но неравенство напрямую следует из неравенства , если в нем вместо b
положить −b
, и принять c=0
.

Решение задач с применением модуля числа

Решение:

Следует понимать, что мы не располагаем числа — 15 ; — 1 ; в порядке возрастания. 4 ; 7, но их модули.

Для этого мы должны определить модули каждого из них:

|-15| = 15

|-1| = 1

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите эти числа в порядке возрастания (от наименьшего к наибольшему):

1, 4, 7, 15 .

Это дает следующую последовательность уравнений,

|-1| = 1

|4| = 4

|7| = 7

|-15| = 15

Следовательно, числа должны располагаться в порядке возрастания их модуля: -1, 4, 7, 7, -15

Ответ: — 1, 4, 4, 7, 7, — 15

|-15| = 15

На координатной прямой мы отметили две точк и-73 и 68. Какой коэффициент числа больше?

Решение:

Представьте, что на координатной прямой на определенном расстоянии от точки O (начало координат) отмечены две точки.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Понятие модуля числа часто кажется студентам пугающим и непонятным. На самом деле, в этой теме по математике 6 класса нет ничего сложного. Чтобы лучше понять вопрос, давайте рассмотрим основные моменты, связанные с понятием коэффициента.

Мы начнем с понятия числовой линии и вектора. Прямая линия — это линия, на которой можно увидеть направление движения, точку 0 (начало координат) и величину единичного перехвата.

Каждое из действительных чисел может быть отмечено на числовой прямой. Независимо от подмножества, размер числа и его десятичные знаки. Прямая линия бесконечна и поэтому подходит абсолютно ко всем числам, кроме комплексных.

Числовая линия часто используется для сравнения различных типов чисел. Если отметить на линии два числа, то число справа будет больше, а число слева — меньше.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Представьте, что на координатной прямой на определенном расстоянии от точки O (начало координат) отмечены две точки.

Модуль — это размер сегмента вектора. То есть, если число обозначено символом модуля, то вычитается параметр направления вектора. В геометрии это необходимо для нахождения сумм векторов и вообще для любых алгебраических операций с векторами. В этом примере невозможно указать и учесть направление, поэтому был придуман модуль.

В алгебре модуль числа означает, что при вычислениях учитывается только размер отрезка, без учета направления. На практике это означает, что

повороты модуля:

Возникает вопрос, почему отрицательное число становится положительным? Знак минус указывает только направление вектора. Символ знака минус указывает направление знака. А знак модуля отменяет параметр направления. Может ли размер сегмента быть отрицательным? Нет, конечно, нет. Таким образом, коэффициент отрицательного числа всегда является положительным числом.

|-15| = 15

В этом уроке мы более подробно рассмотрим понятие коэффициента числа.

Модуль — это расстояние между началом координат и числом на координатной прямой. Поскольку расстояние никогда не бывает отрицательным, модуль всегда неотрицателен. Поэтому модуль числа 3 равен 3, так же как модуль числ а-3 равен 3.

Предположим, что на координатной прямой расстояние между целыми числами равно одному шагу. Если теперь обозначить числ а-3 и 3, то их расстояние от начала координат равно трем шагам:

Коэффициент — это не только расстояние между началом координат и числом. Модулем также является расстояние между любыми двумя числами на координатной прямой. Это расстояние выражается как разность между этими числами с помощью символа модуло:

Основные свойства модуля

Первое свойство модуля

То есть, если \( \mathbf{a}\) – число положительное, то его модуль будет равен этому же числу.

Если \( \mathbf{a}\text{ }>\text{ }\mathbf{0},\) то \( \displaystyle \left| a \right|=a\).

Если \( a\) – отрицательное число, то его модуль равен противоположному числу.

Если \( a\text{ }<\text{ }\mathbf{0},\) то \( |\mathbf{a}|\text{ }=\text{ }-\mathbf{a}\)

А если \( a=0\)? Ну, конечно! Его модуль также равен \( 0\):

Если \( a=0\), то \( |\mathbf{a}|=\mathbf{a}\), или \( \displaystyle \left| 0 \right|=0\).

Из этого следует, что модули противоположных чисел равны, то есть:

\( \left| -4 \right|\text{ }=\text{ }\left| 4 \right|\text{ }=\text{ }4;\)\( \left| -7 \right|\text{ }=\text{ }\left| 7 \right|\text{ }=\text{ }7.\)А теперь потренируйся:

• \( \left| 9 \right|\text{ }=\text{ }?;\)
• \( \left| -3 \right|\text{ }=\text{ }?;\)
• \( \left| 16 \right|\text{ }=\text{ }?;\)
•  \( \left| 8 \right|\text{ }=\text{ }?;\)
• \( \left| -17 \right|\text{ }=\text{ }?.\)

Ответы: 9; 3; 16; 8; 17.

Довольно легко, правда? А если перед тобой вот такое число: \( \left| 2-\sqrt{5} \right|=?\)

Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.

Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:

• если значение выражения больше нуля, то просто выносим его из-под знака модуля,
• если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.

Ну что, попробуем? Оценим \( 2-\sqrt{5}\):

\( 2<\sqrt{5}\) (Забыл, что такое корень? Бегом повторять!)

Если \( 2<\sqrt{5}\), то какой знак имеет \( 2-\sqrt{5}\)? Ну конечно, \( 2-\sqrt{5}<0\)!

А, значит, знак модуля раскрываем, меняя знак у выражения:

\( \left| 2-\sqrt{5} \right|=-\left( 2-\sqrt{5} \right)=-2+\sqrt{5}=\sqrt{5}-2\)Разобрался? Тогда попробуй сам:

• \( \left| \sqrt{3}-1 \right|=?\)
• \( \left| 3-\sqrt{7} \right|=?\)
• \( \left| 2-\sqrt{7} \right|=?\)
• \( \left| \sqrt{13}-4 \right|=?\)

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

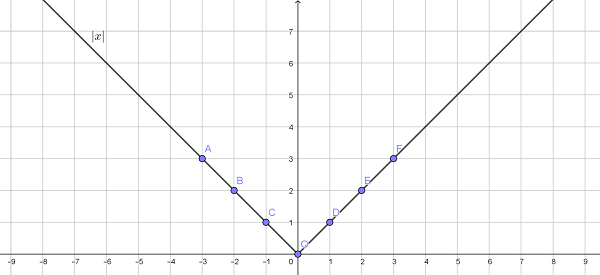
Объяснение: из рисунка видно, что график симметричен относительно оси Y.

Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

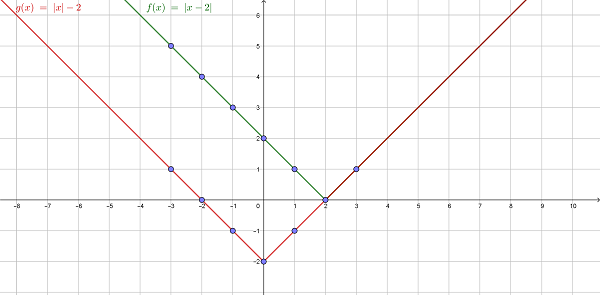
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

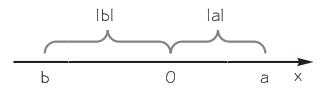
Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.

Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.

Количественный смысл

Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .

Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.

Вывод

Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.

Ваша цель:

четко знать определение модуля действительного числа;

понимать геометрическую интерпретацию модуля действительного числа и уметь применять ее при решении задач;

знать свойства модуля и уметь применять при решении задач;

уметь представление о расстоянии между двумя точками координатной прямой и уметь использовать его при решении задач.

Входная информация

Понятие модуля действительного числа.

Модулем действительного числа называют само это число , если , и противоположны ему число , если

Модуль числа обозначают и записывают:

Геометрическая интерпретация модуля

.
Геометрически
модуль действительного числа есть расстояние от точки, изображающей данное число на координатной прямой, до начала отсчета.

Решение уравнений и неравенств с модулями на основе геометрического смысла модуля
.
Пользуясь понятием «расстояние между двумя точками координатной прямой» можно решать уравнения вида или неравенства вида , где вместо знака может стоять любой из знаков .

Пример.
Решим уравнение .

Решение.
Переформулируем задачу геометрически. Поскольку -это расстояние на координатной прямой между точками с координатами и , значит, требуется найти координаты таких точек, расстояние от которых до точек с координатой 1 равно 2.

Короче, на координатной прямой найти множество координат точек, расстояние от которых до точки с координатной 1 равно 2.

Решим эту задачу. Отметим на координатной прямой точку, координата которой равна 1 (рис. 6) На две единицы от этой точки удалены точки, координаты которых равны -1 и 3. Значит, искомое множество координат точек есть множество, состоящее из чисел -1 и 3.

Ответ: -1; 3.

Как найти расстояние между двумя точками координатной прямой.

Число, выражающее расстояние между точками и ,
называют расстоянием между числами и .

Для любых двух точек и координатной прямой расстояние

.

Основные свойства модуля действительного числа:

3. ;

7. ;

8. ;

9. ;

При имеем:

11. тогда только тогда, когда или ;

12. тогда только тогда, когда ;

13. тогда только тогда, когда или ;

14. тогда только тогда, когда ;

11. тогда только тогда, когда .

Практическая часть

Задание 1.

Возьмите чистый лист бумаги и на нем запишите ответы ко в сем устным упражнениям, приведенным ниже.

Свои ответы сверьте с ответами или краткими указаниями, помещенными в конце учебного элемента в рубрике «Ваш помощник».

1.
Раскройте знак модуля:

а) |–5|; б) |5|; в) |0|; г) |p|.

2.
Сравните между собой числа:

а) || и –; в) |0| и 0; д) – |–3| и –3; ж) –4|а
| и 0;

б) |–p| и p; г) |–7,3| и –7,3; е) |а
| и 0; з) 2|а
| и |2а
|.

3.
Как при помощи знака модуля записать, что по крайней мере одно из чисел а
, b
или с
отлично от нуля?

4.
Как при помощи знака равенства записать, что каждое из чисел а
, b
и с
равно нулю?

5.
Найдите значение выражения:

а) |а
| – а
; б) а
+ |а
|.

6.
Решите уравнение:

а) |х
| = 3; в) |х
| = –2; д) |2х
– 5| = 0;

б) |х
| = 0; г) |х
– 3| = 4; е) |3х
– 7| = – 9.

7.
Что можно сказать о числах х
и у
, если:

а) |х
| = х
; б) |х
| = –х
; в) |х
| = |у
|?

8.
Решите уравнение:

а) |х
– 2| = х
– 2; в) |х
– 3| =|7 – х
|;

б) |х
– 2| = 2 – х
; г) |х
– 5| =|х
– 6|.

9.
Что можно сказать о числе у
, если имеет место равенство:

а) ïх
ï = у
; б) ïх
ï = –у
?

10.
Решите неравенство:

а) |х
| > х
; в) |х
| > –х
; д) |х
| £ х
;

б) |х
| ³ х
; г) |х
| ³ –х
; е) |х
| £ –х
.

11.
Укажите все значения а, для которых имеет место равенство:

а) |а
| = а
; б) |а
| = –а
; в) а
– |–а
| =0; г) |а
|а
= –1; д) = 1.

12.
Найдите все значения b
, для которых имеет место неравенство:

а) |b
| ³ 1; б) |b
| b
| £ 0; г) |b
| ³ 0; д) 1 b
|

С некоторыми видами следующих заданий вы могли встречаться на уроках математики. Самоопределитесь, какие из следующих заданий вам необходимо выполнить. В случае затруднений обращайтесь к рубрике «Ваш помощник», за консультацией к учителю или за помощью к товарищу.

Задание 2.
Исходя из определения модуля действительного числа, решите уравнение:

Задание 4.
Расстояние между точками, изображающими действительные числа α
и β
на координатной прямой, равно | α
– β
|. Пользуясь этим, решите уравнение.