Простейшие задачи в координатах

Введение прямоугольной системы координат

Даже если в формулировке задачи коор-ты и вектора прямо не упоминаются, может быть полезным самостоятельно добавить в нее прямоугольную систему координат. Это позволит использовать формулы, используемые в методе коор-т, для решения задачи.

Задание. Докажите, что если в параллелограмме сложить квадраты всех его сторон, то получится то же число, что и при сложении квадратов диагоналей этого параллелограмма.

Решение. Расположим систему коор-т таким образом, одна из сторон параллелограмма находилась на оси Ох, причем одна ее вершина совпадала с началом коор-т, а другая имела положительную коор-ту х:

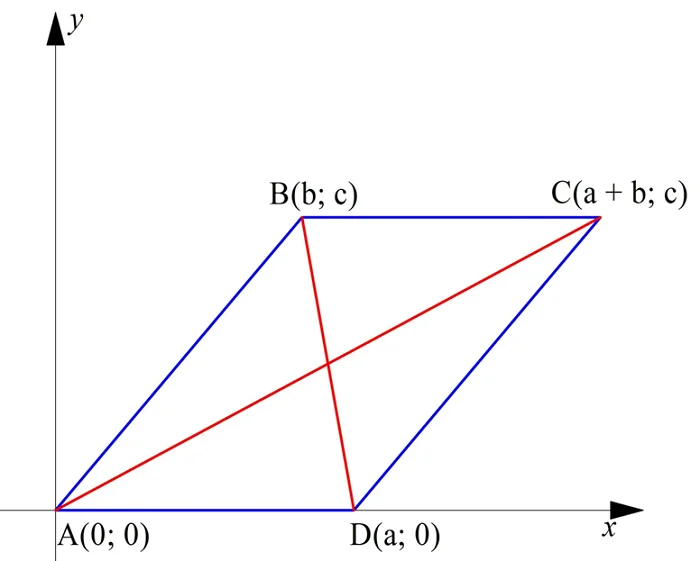
Пусть вершина А находится в начале коор-т, и тогда она имеет коор-ты (0; 0). Вершина D лежит на Ох, тогда ее ордината равна нулю, а абсциссу обозначим буквой а. Точка В имеет произвольные коор-ты (b; с), коор-ты же точки С можно рассчитать. Сначала заметим, что вектор коор-ты вектора АВ совпадают с коор-тами точки В, так как он является радиус-вектором:

Вектора АВ и DC равны, потому что они лежат на параллельных прямых и имеют одинаковую длину:

Итак, коор-ты С – это (а + b; с).

Теперь мы должны длину каждой стороны параллелограмма и возвести ее в квадрат

Обратите внимание, что если расстояние между точками рассчитывается по формуле

Равенство доказано.

Задание. В равнобедренном треугольнике длина основания составляет 80 см, а опущенная на нее медиана имеет длину 160 см. Вычислите длины двух других медиан.

Решение. Пусть АВС – рассматриваемый в задаче треугольник, причем АВ – его основание. Расположим систему коор-т так, чтобы ее начало совпадало с точкой, в которой медиана пересекается с основанием:

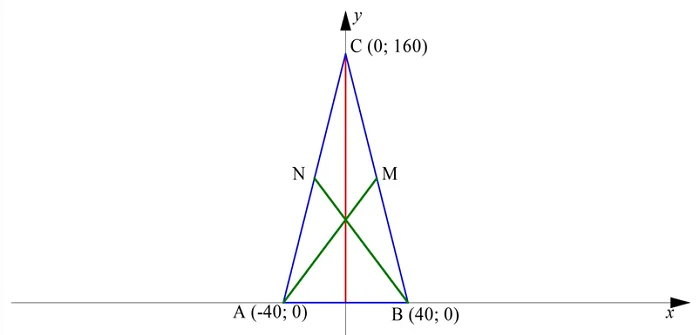
В этом случае вершина, из которой опущена медиана, будет иметь коор-ты (0; 160), а две другие вершины будут иметь коор-ты (– 40; 0) и (40; 0).

Нам надо найти длину двух других медиан АM и BN. Они одинаковы по длине, поэтому достаточно найти длину только одной из них, например, АМ. Для этого сначала найдем коор-ты М, которая является серединой ВС:

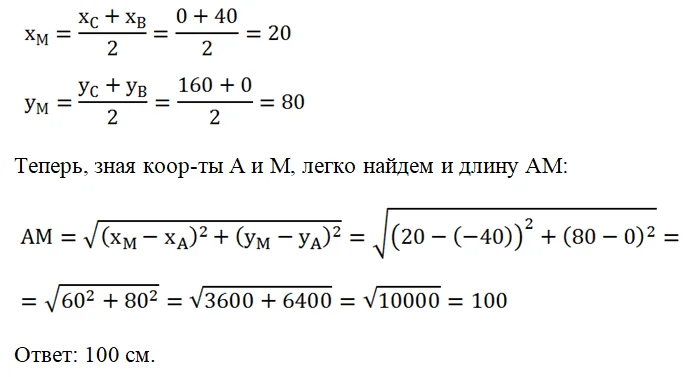
Сегодня мы познакомились с важнейшими формулами, используемыми в методе коор-т, и научились решать некоторые простейшие задачи. В будущем мы узнаем о более сложных задачах, в которых будут фигурировать не только отрезки и многоугольники, но и окружности.

Глава 28. Расстояние между двумя точками. Деление отрезка в данном отношении

Расстояние d между двумя точками
(,
,)
и
(,
,)
в пространстве определяется формулой

Координаты x, y, z
точки М, которая делит отрезок , ограниченный
точками
(,
,) и
(,
,), в отношении ,
определяется по формулам

,
,
.

В частности, при имеет координаты
середины данного отрезка:

,
,
.

Даны точки A(1; -2; -3), B(2; -3; 0), C(3; 1;
-9), D(-1; 1; -12). Вычислить расстояние между 1). А и С, 2). B
и D, 3). C и D.

Вычислить
расстояния от начала координат О до точек A(4; -2; -4),
B(-4; 12; 6), C(12; -4; 3), D(12; 16; -15).

Доказать, что
треугольник с вершинами A(3; -1; 2), B(0; -2; 2), C(-3; 2; 1)
равнобедренный.

Доказать, что
треугольник с вершинами A₁(3; -1;
6), A₂(-1; 7; -2), A₃(1; -3; 2) прямоугольный.

Определить, есть ли
тупой угол среди внутренних углов треугольника с
вершинами M₁(4; -1; 4), M₂(0; 7; -4),
M₃(3; 1; -2).

Доказать, что
внутренние углы треугольника M(3; -2; 5), N(-2; 1; -3), P(5; 1;
-1) острые.

На ось абсцисс
найти точку, расстояние от которой до точки А(-3; 4; равно 12.

На оси ординат
найти точку, равноудаленную отточек А(1; -3; 7) и В(5;
7; -5).

Найти центр C и
радиус R шаровой поверхности, которая проходит
через точку P(4; -1; -1) и касается всех трех
координатных плоскостей.

Даны вершины M₁(3; 2; -5), M₂(1; -4; 3), M₃(-3; 0; 1) треугольника. Найти середины его
сторон.

Даны вершины A(2; -1; 4).
B(3; 2; -6), C(-5; 0; 2) треугольника. Вычислить длину его
медианы, проведенной из вершины А.

Центр масс
однородного стержня находится в точке С(1; -1; 5),
один из его концов есть точка A(-2; -1; 7). Определить
координаты другого конца стержня.

Даны две вершины A(2;
-3; -5), B(-1; 3; 2) параллелограмма ABCD и точка
пересечения его диагоналей E(4; -1; 7). Определить
две другие вершины этого параллелограмма.

Даны три вершины A(3;
-4; 7), B(-5; 3; -2), C(1; 2; -3) параллелограмма ABCD. Найти его
четвертую вершину D, противоположную B.

Даны три вершины A(3;
-1; 2), B(1; 2; -4), C(-1; 1; 2) параллелограмма ABCD. Найти его
четвертую вершину D.

Отрезок прямой,
ограниченный точками A(-1; 8; 3), B(9; -7; -2), разделен
точками C, D, E. F на пять равных частей. Найти
координаты этих точек.

Определить
координаты концов отрезка, который точками C(2; 0;
2), D(5; -2; 0) разделен на три равные части

Даны вершины
треугольника A(1; 1; -1), B(2; -1; 3), C(-4; 7; 5). Вычислить
длину биссектрисы его внутреннего угла при
вершине B.

Даны вершины
треугольника A(1; -1; -3), B(2; 1; -2), C(-5; 2; -6). Вычислить
длину биссектрисы его внутреннего угла при
вершине А.

В вершинах
тетраэдра A(x₁, y₁, z₁),
B(x₂, y₂, z₂), C(x₃, y₃, z₃),
D(x₄, y₄, z₄) сосредоточены
равные массы. Найти координаты центра масс этой
системы.

В вершинах
тетраэдра A₁(x₁, y₁, z₁),
A₂(x_, y₂, z₂), A₃(x₃, y₃,
z₃), A₄(x₄, y₄, z₄) сосредоточены массы m₁, m₂,
m₃, m₄. Найти координаты
центра масс этой системы.

Прямая проходит
через две точки M₁(-1; 6; 6) и M₂(3; -6; -2). Найти
точки ее пересечения с координатными
плоскостями.

Текст издания: Д.В.Клетеник «Сборник задач по аналитической геометрии». М., Наука, Физматлит, 1998Решение задач: 2004-2013, Кирилл Кравченко, http://a-geometry.narod.ru/, http://kirill-kravchenko.narod.ru/

Различные системы координат на плоскости и в пространстве.

§ 1. Декартова система координат на плоскости

Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.

Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.

Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.

Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).

§ 2. Полярная система координат на плоскости

Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.

Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.

Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ0.

Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то 

x = ρ∙cosφ, 

y = ρ∙sinφ.

В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.

С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..

В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.

§3. Декартова система координат в пространстве

Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.

§4. Цилиндрическая система координат в пространстве

Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось. 

Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:

x = ρ·cosφ,

y = ρ·sinφ,

z = z.

§5. Сферическая система координат в пространстве

Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней — точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.

Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:

x = ρ·sinθ·cosφ,

y = ρ·sinθ·sinφ,

z = ρ·cosθ.

Проекция вектора онлайн

Алгебраическая проекция вектора

Пр_ab = |b|cos(a,b) или

a

Инструкция.

Пp_ababab

Классификация проекций вектора

Виды проекций по определению проекция вектора

1. Геометрическая проекция вектора AB на ось (вектор) называется вектор A’B’, начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
2. Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A’B’, взятая со знаком + или -, в зависимости от того, имеет ли вектор A’B’ то же направление, что и ось (вектор).

Виды проекций по системе координат

1. проекции на плоскости (система координат OX,OY). Пример: a(2;-3), a=2i-3j

2. проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k

3. проекции в N-мерном пространстве

AC’=AB’+B’C’

Пр_ab = |b|·cos(a,b)

Виды проекций вектора

1. проекция на ось OX.
2. проекция на ось OY.
3. проекция на вектор.

Проекция на ось OX	Проекция на ось OY	Проекция на вектор
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.	Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.	Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.	Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).	Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).

1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор).

Пример 1. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.

Пример 2. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120o. Длина |b| вектора b равна 4, поэтому пр_ab=4·cos120o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.

Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).
Координаты вектора: MN(4-1;5-1) = MN(3;4)
Тогда модуль вектора MN равен:
Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.

Пример 4. Найти проекцию вектора c на вектор d;
с = АС = (-2;-1;3), d = CB(-5;-3;3)
Найдем проекцию вектора AC на вектор BC

Пример 5. Найти проекцию пр_b(-2a+4b)
где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π
Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n

222о

пр_b(-2a+4b) = пр_b(12m+2n) =

Расположение на плоскости

Пусть существуют две плоскости, образующие между собой прямой угол. Их точка пересечения A является началом отсчёта любой из них. Если ось одной плоскости обозначить за X, а второй — за Y, то общим для них пространством будет Axy. Ось, совпадающая с X, называется абсциссой, а Y — ординатой. Единица длины для них одинакова. Пересекающиеся оси образуют четверти. Нумерацию принято вести с верхней правой части против часовой стрелки.

Пусть в плоскости Axy находится произвольная точка. Проведя с неё перпендикуляры на оси, получим два пересечения. Числовые значения в этих местах и будут определять положение A на плоскости, то есть её координаты. Записывают их как A (x, y) и называют декартовыми. Таким образом, нахождение A сводится к определению двух точек, лежащих на осях x и y.

Когда точка располагается на оси X, то её ордината имеет нулевое значение, а если Y — абсцисса. В зависимости от того, в какой четверти находится исследуемый объект, определяется знак его координат. В первой оба числа положительные, а в третьей — отрицательные. Во второй же абсцисса имеет положительное значение, а ордината — отрицательное. В третьей же знаки координат обратные второй четверти.

Естественно, что каждой точке на плоскости соответствует пара чисел. Любая фигура состоит из множества точек. Проведя учёт точек и зная их взаимоотношение относительно друг друга, можно изучить свойство объекта. Эти вычисления позволяет выполнить алгебра и арифметика. Поэтому появляется возможность решать геометрические задачи наглядными алгебраическими способами.

В этом и лежит основа использования метода координат в пространстве. Формулы, применяемые при расчётах, хотя и выглядят устрашающе, на самом деле запоминаются легко. Правда, для этого следует выполнить несколько практических заданий.

Рассмотрим пример алгоритма для нахождения середины отрезка при помощи циркуля и линейки

Алгоритм деления отрезка АВ пополам:

1) поставить ножку циркуля в точку А;

2) установить раствор циркуля равным длине отрезка АВ;

4) поставить ножку циркуля в точку В;

6) через точки пересечения окружностей провести прямую;

7) отметить точку пересечения этой прямой с отрезком АВ.

Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное законченное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Предписания алгоритма надо выполнять последовательно одно за другим, в соответствии с указанным порядком их записи. Выполнение всех предписаний гарантирует правильное решение задачи. Данный алгоритм будет понятен исполнителю, умеющему работать с циркулем и знающему, что такое поставить ножку циркуля, провести окружность и т. д.

8. Основные элементы блок-схем. Линейные, разветвляющиеся, цикличные, комбинированные алгоритмы.

Выделяют следующие виды алгоритмов: линейный, разветвляющийся, циклический, комбинированный.

Линейными

Разветвляющимсяназывается алгоритм, в котором действие выполняется по одной из возможных ветвей решения задачи, в зависимости от выполнения условий. В отличие от линейных алгоритмов, в которых команды выполняются последовательно одна за другой, в разветвляющиеся алгоритмы входит условие, в зависимости от выполнения или невыполнения которого выполняется та или иная последовательность команд (действий).

В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинно) или не соблюдаться (быть ложно). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд.

В зависимости от того, в обоих ветвях решения задачи находится последовательность команд или только в одной разветвляющиеся алгоритмы делятся на полные и не полные (сокращенные).

Стандартные блок-схемы разветвляющегося алгоритма приведены ниже:

Циклическим называется алгоритм, в котором некоторая часть операций (тело цикла — последовательность команд) выполняется многократно. Однако слово «многократно» не значит «до бесконечности». Организация циклов, никогда не приводящая к остановке в выполнении алгоритма, является нарушением требования его результативности — получения результата за конечное число шагов.

Перед операцией цикла осуществляются операции присвоения начальных значений тем объектам, которые используются в теле цикла. В цикл входят в качестве базовых следующие структуры:

блок, называемый телом цикла

Существуют три типа циклов:

3. Цикл с параметром (разновидность цикла с предусловием)

Если тело цикла расположено после проверки условий , то может случиться, что при определенных условиях тело цикла не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется циклом c предусловием.

Возможен другой случай, когда тело цикла выполняется по крайней мере один раз и будет повторяться до тех пор, пока не станет ложным условие. Такая организация цикла, когда его тело расположено перед проверкой условия, носит название цикла с постусловием.

Цикл с параметром является разновидностью цикла с предусловием. Особенностью данного типа цикла является то, что в нем имеется параметр, начальное значение которого задается в заголовке цикла, там же задается условие продолжения цикла и закон изменения параметра цикла. Механизм работы полностью соответствует циклу с предусловием, за исключением того, что после выполнения тела цикла происходит изменение параметра по указанному закону и только потом переход на проверку условия.

Стандартные блок-схемы циклических алгоритмов приведены ниже:

9. Алгоритмические процедуры и функции, их взаимодействие.

Процедура является блоком операторов Visual Basic, объединенных оператором объявления (FunctionSubOperator, Get, Set) и соответствующего объявления End. Все выполняемые инструкции в Visual Basic должны находиться в пределах некоторой процедуры.

Процедура вызывается из какой-либо другой части кода. Подобная операция известна как вызов процедуры. После завершения процедуры она возвращает управление коду, вызвавшему ее, который называется вызывающий код. Вызывающий код — это инструкция или выражение в составе инструкции, которое определяет процедуру по имени и передает ей управление.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Правила нахождения координат середины отрезка, формулы

Середина отрезка на координатной прямой

Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа x_A и x_B, а точка С делит AB пополам. Определите координату x_C, соответствующую С. 

Так как C — это середина AB, то справедливо следующее равенство:

\(\left|AC\right|=\left|CB\right|\)

Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:

\(\left|AC\right|=\left|CB\right|\Leftrightarrow\left|x_C-x_A\right|=\left|x_B-x_C\right|\)

Опустим знак модуля и получим справедливость двух выражений:

\(x_C-x_A=x_B-x_C\)

\(x_C-x_A=-\left(x_B-x_C\right)\)

Исходя из первого равенства, получим формулу нахождения x_C, согласно которой координата точки С равна половине суммы координат A и B:

\(x_C=\frac{x_A+x_B}2\)

Следствием второго равенства будет следующее утверждение: 

\(x_A=x_B\)

Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:

\(x_C=\frac{x_A+x_B}2\)

Середина отрезка на плоскости

В декартовой системе координат Oxy расположены две точки A(x_A,y_A) и B(x_B,y_B), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат x_C и y_C, соответствующих С.

Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат A_x, A_y; B_x, B_y; C_x, C_y — это проекции исходных точек.

По построению прямые AA_x, BB_x, CC_x относительно друг друга находятся параллельно. Прямые AA_y, BB_y, CC_y не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:

\(A_xC_x=C_xB_x\)

\(A_yC_y=C_yB_y\)

Это значит, что C_x и C_y являются серединами отрезков A_xB_x и A_yB_y соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:

\(x_C=\frac{x_A+x_B}2\)

\(y_C=\frac{y_A+y_B}2\)

Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(x_A,y_A) и B(x_B,y_B), вычисляются следующим образом:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2\right)\)

Середина отрезка в пространстве

Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(x_A, y_A, z_A) и B(x_B, y_B, z_B). C(x_C, y_C, z_C) — это центр АВ. Задание заключается в том, чтобы определить x_C, y_C, z_C.

Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — A_x, A_y, A_z; B_x, B_y, B_z;C_x, C_y, C_z — проекции точек A, B, C на них.

Воспользуемся теоремой Фалеса:

\(\left|A_xC_x\right|=\left|C_xB_x\right|\)

\(\left|A_yC_y\right|=\left|C_yB_y\right|\)

\(\left|A_zC_z\right|=\left|C_zB_z\right|\)

Исходя из полученных равенств следует, что C_x, C_y, C_z — делят A_xB_x, A_yB_y, A_zB_z пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(x_A,y_A,z_A) и B(x_B,y_B,z_B) используем формулу:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)