Как найти расстояние от точки до плоскости: формула и методика. пример задачи

Упражнение

Дано : отрезок общего положения – АВ.

Определить : способом вращения истинную величину отрезка и углы наклона его к плоскостям проекций.

1. Выберем ось вращения m⊥π₁ и проходящую через точку В (Рисунок 4.6).

На плоскости проекций π₂ проекция траектории перемещения точки А – прямая,

A_2 \overline\perp m_2\;u\;A_2\overline\parallel\pi_2/\pi_1

На плоскости проекций π₁ проекция траектории перемещения точки А – окружность радиусом |А₁В₁|.

Повернем отрезок до положения, параллельного плоскости проекций π₂. Получим натуральную величину отрезка.

Угол наклона отрезка АВ к плоскости проекций π₁ будет угол \alpha=\angle\widehat_2> .

Для того, чтобы определить угол наклона АВ к плоскости проекций π₂, надо ввести новую ось вращения перпендикулярно π₂ и повторить построения.

Параллельность прямой и плоскости.

Пусть известен направляющий вектор прямой \(\boldsymbol{a}(\alpha_{1}, \alpha_{2}, \alpha_{3})\), а плоскость задана одним из уравнений \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})=0\) или \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{p}, \boldsymbol{q})=0\). Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда, когда соответственно \((\boldsymbol{a}, \boldsymbol{n}=0)\) или \((\boldsymbol{a}, \boldsymbol{p}, \boldsymbol{q}=0)\). Если плоскость задана линейным уравнением \(Ax+By+Cz+D=0\), то по , доказанному ранее, условие параллельности —
$$
A\alpha_{1}+B\alpha_{2}+C\alpha_{3}=0.\label{ref3}
$$

Пусть прямая задана системой уравнений
$$
\left\{
\begin{array}{l}
A_{1}x+B_{1}y+C_{1}z+D_{1}=0,\\
A_{2}x+B_{2}y+C_{2}z+D_{2}=0.
\end{array}
\right.\nonumber
$$
Тогда по утверждению 10 условие \eqref{ref3} переписывается в виде
$$
A\begin{vmatrix}
B_{1}& C_{1}\\
B_{2}& C_{2}
\end{vmatrix}
+ B\begin{vmatrix}
C_{1}& A_{1}\\
C_{2}& A_{2}
\end{vmatrix}
+ C\begin{vmatrix}
A_{1}& B_{1}\\
A_{2}& B_{2}
\end{vmatrix}
= 0.\nonumber
$$
или
$$
\begin{vmatrix}
A& B& C\\
A_{1}& B_{1}& C_{1}\\
A_{2}& B_{2}& C_{2}
\end{vmatrix}
= 0.\label{ref4}
$$

Легко проверить, что все приведенные здесь условия являются не только необходимыми, но и достаточными.

Из формулы \eqref{ref4} следует, что три плоскости пересекаются в одной точке тогда и только тогда, когда коэффициенты их уравнений удовлетворяют условию
$$
\begin{vmatrix}
A& B& C\\
A_{1}& B_{1}& C_{1}\\
A_{2}& B_{2}& C_{2}
\end{vmatrix}
\neq 0.\label{ref5}
$$
Действительно, это неравенство означает, что прямая, по которой пересекаются две плоскости, не параллельна третьей.

Определение расстояния от точки до плоскости

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.

1. Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.
2. Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.

Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.

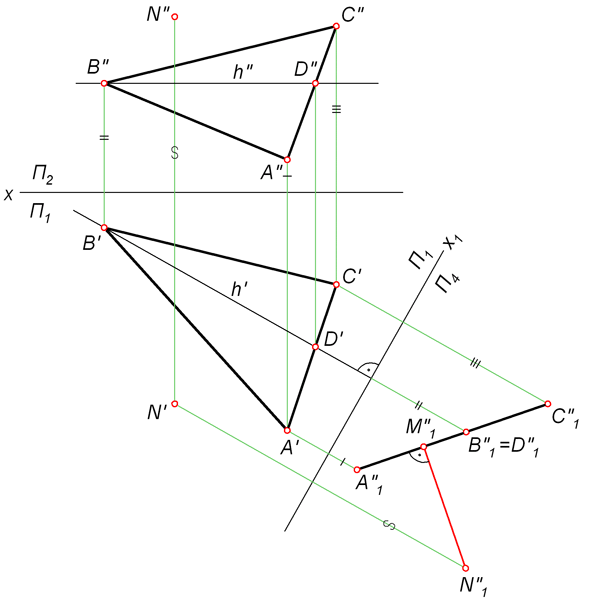
• Через вершину B» треугольника A»B»C» проводим проекцию h» горизонтали h. По линиям связи находим h’.
• Переводим ABC в проецирующее положение. Для этого перпендикулярно h вводим новую фронтальную плоскость П₄. Проецируем на неё точку N и треугольник ABC.
• Из точки N»₁ проводим N»₁M»₁ ⊥ A»₁C»₁. Длина отрезка N»₁M»₁ – искомое расстояние между плоскостью треугольника ABC и точкой N.

Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами. В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h_0β.

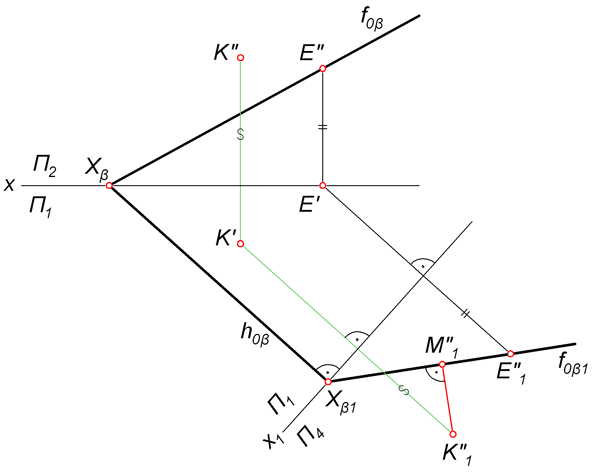
• Переводим плоскость β в проецирующее положение. Для этого перпендикулярно следу h_β вводим дополнительную фронтальную плоскость П₄. На прямой f_β берем произвольную точку E, определяем её проекции E», E’ и E»₁. Через E»₁ и X_α1 проводим прямую f_β1, которая является следом плоскости β на П₄. По линии связи определяем проекцию K»₁ точки K.
• Из K»₁ проводим перпендикуляр K»₁M»₁ в направлении прямой f_β1. Длина отрезка K»₁M»₁ – величина искомого расстояния от K до β.

Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.

Источник

Примеры задач

Задание 1
На плоскости даны две точки: и. Найдем расстояние между ними.

Решение:
Воспользуемся первой формулой, представленной выше:

Задание 2
Найдем расстояние между точками и.

Решение:
Применим соответствующую формулу, подставив в нее известные нам значения:

Публикации по теме:

• Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра прямоугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение объема куба: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение площади прямоугольного параллелепипеда: формула и пример Формула Герона для треугольника Теорема о трех перпендикулярах Теорема Фалеса: формулировка и пример решения задачи Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равнобедренного треугольника: теория и задача Определение и свойства медианы в равнобедренном треугольнике Определение и свойства медианы равностороннего треугольника Определение и свойства высоты треугольника Формулы для нахождения высоты треугольника Нахождение радиуса вписанной в квадрат окружности Нахождение радиуса описанной вокруг квадрата окружности Что такое ромб: определение, свойства, признаки Нахождение длины дуги сектора круга Нахождение площади сегмента круга Что такое параллелограмм: определение, свойства, признаки Нахождение высоты прямоугольной трапеции Нахождение радиуса вписанного в куб шара Что такое куб: определение, свойства, формулы Что такое шар (сфера): определение, свойства, формулы Нахождение площади шарового слоя Нахождение объема шарового слоя Что такое конус: определение, элементы, виды Что такое пирамида: определение, элементы, виды, варианты сечения Основные свойства пирамиды Что такое правильная пирамида: определение, виды, свойства Нахождение радиуса вписанного в цилиндр шара (сферы) Нахождение радиуса/площади/объема описанной вокруг цилиндра сферы (шара) Что такое эллипс: определение, основные элементы, уравнение Что такое правильный многоугольник: определение, признаки, элементы, виды Свойства правильного многоугольника Что такое прямая: определение, свойства, взаимное расположение Сумма и разность векторов Умножение вектора на число Нахождение угла между векторами Нахождение проекции вектора: формула, примеры

Расстояние между двумя точками — это длина отрезка (D), который получится, если их соединить.

Нахождение расстояния между двумя точками

В данной публикации мы рассмотрим, чему равно расстояние между двумя точками, и по какой формуле оно считается (на плоскости и в пространстве). Также разберем примеры решения задач по этой теме.

скрыть

• Расчет расстояния между двумя точками Примеры задач

Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).

Расчет расстояния между двумя точками

Расстояние между двумя точками это длина отрезка d, который получится, если их соединить.

06.05.2017 18:31:27

2017-05-06 18:31:27

Любые данныеЛюбые данные Любые данные Любые данные

4.3. Определение истинной величины треугольника способом вращения

Пусть плоскость σ задана треугольником. Необходимо определить истинную величину треугольника (Рисунок 4.7).

Одним поворотом вокруг оси, перпендикулярной к плоскости проекций, истинную форму треугольника получить нельзя (так же как и введением одной ДПП).

Вращая вокруг оси m, перпендикулярной π₁ можно расположить плоскость ΔАВС⊥π₂ (а вращая вокруг оси n⊥π₂ можно расположить плоскость ΔАВС⊥π₁).

1. Положим σ’ должна быть перпендикулярна π₂. Для чего построим CD – горизонталь h плоскости σ. Введём первую ось вращения m⊥π₁, например, через точку С.
2. Повернём треугольник вокруг m до положения, когда \overline\perp\pi_2\Rightarrow\overline_1\overline_1\perp\pi_2/\pi_1 На основании 3-го свойства, новая горизонтальная проекция треугольника \overline по величине должна равняться A₁B₁C₁, а фронтальная проекция треугольника будет представлять отрезок.
3. Введём вторую ось вращения n⊥π₂ через точку \overline_2 . Повернём фронтальную проекцию \overline в новое положение \overline\overline\overline>\parallel\pi_2/\pi_1 . На π₁ получим треугольник \overline\overline\overline> , равный истинной величине треугольника АВС.

Нахождение расстояния от точки до плоскости онлайн-калькулятором

В сервис заложен алгоритм, который находит расстояние по формуле:

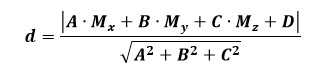
Чем полезна программа:

• Отсутствием платежей. Воспользоваться любым расчетом на сайте можно бесплатно. Школьники смогут обойтись без репетиторов при подготовке домашних заданий и повторении тем к поступлению в университет.
• Круглосуточным доступом без ограничений в расчетах. Лимита на вычисления нет. Любой пользователь может отправлять необходимое количество запросов в каждом из разделов.
• Подробными действиями. Сервис выдает последовательное решение и ответ. Имея перед глазами действия легче свериться с собственными расчетами и найти ошибку.
• Комплексом расчетов внутри программы. Вам не придется самим производить никаких промежуточных вычислений. Требуется только ввести данные и получить результат.

Если у вас не получилось разобраться в теме с помощью программы, напишите консультанту. Он найдет преподавателя из нашего штата, который доходчиво и за короткое время объяснит непонятный материал. Также мы оказываем услуги по решению задач, предоставляем дистанционную помощь на контрольных, зачетах, экзаменах.

Расстояние от точки до плоскости − теория, примеры и решения

Для нахождения расстояния от точки M до плоскости α, необходимо найти расстояние от точки M до проекции точки M на плоскость α:

Нахождение расстояния от точки до плоскости содержит следующие шаги:

1. построение прямой L, проходящей через точку M и перпендикулярной плоскости α.
2. нахождение точки M₁ пересечения плоскости α с прямой L(Рис.1).
3. вычисление расстояния между точками M и M₁.

1. Общее уравнение плоскости имеет вид:

(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M(x, y, z) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M(x, y, z) и ортогональной плоскости (1) имеет следующий вид:

(3)

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

(4)

2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x)+B(Bt+y)+C(At+z)+D=0,

A 2 t+Ax+B 2 t+By+C 2 t+Cz+D=0,

(5)

3. Найдем, наконец, расстояние от точки M до плоскости (1). Очевидно, что расстояние от точки M до плоскости (1) − это расстояние от точки M до точки M₁. А это расстояние вычисляется так:

Учитывая значение параметра t, имеем:

(6)

Пример 1. Найти расстояние от точки M(2, -1, -9/31) до плоскости

(7)

Нормальный вектор плоскости имеет вид:

Подставляя координаты точки M и нормального вектора плоскости в (5), получим:

(8)

Из выражений (4) находим:

Проекцией точки M(2, -1, -9/31) на плоскость (7) является точка:

.

Вычислим расстояние между точками M и M₁:

.

.

Расстояние от точки M(2, -1, -9/31) до плоскости (7):

Понятие перпендикуляра

Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.

Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:

Запомним некоторые геометрические термины. В таком построении:

• отрезок МН – это наклонная;
• отрезок НК – это проекция наклонной, или просто проекция;
• К – основание перпендикуляра;
• Н – основание наклонной.

Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).

Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.

Полупространство.

Определение.

Пусть даны плоскость \(P\) и определенный ее нормальный вектор \(\boldsymbol{n}\). Полупространством, определяемым \(P\) и \(\boldsymbol{n}\), называется множество точек \(M\) таких, что для некоторой точки \(M_{0}\) на плоскости вектор \(\overrightarrow{M_{0}M}\) составляет с \(\boldsymbol{n}\) угол, не больший \(\pi/2\).

Если \(\boldsymbol{r}\) — радиус-вектор точки \(M\), а \(\boldsymbol{r}_{0}\) — точки \(M_{0}\), то определение полупространства, эквивалентно неравенству \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Это неравенство и есть уравнение полупространства.

Нетрудно проверить, что определение полупространства не зависит от выбора точки \(M_{0}\). Действительно, если \(M_{1}(\boldsymbol{r}_{1})\) — другая точка плоскости, то вектор \(\boldsymbol{a}=\boldsymbol{r}_{1}-\boldsymbol{r}_{0}\) лежит в плоскости, перпендикулярен \(\boldsymbol{n}\), и мы имеем
$$
(\boldsymbol{r}-\boldsymbol{r}_{1}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}-\boldsymbol{a}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}).\nonumber
$$

Мы получим уравнение полупространства в координатной форме, если вспомним, что согласно утверждению 3 выражение \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})\) в координатах записывается линейным многочленом \(Ax+By+Cz+D\). Итак, полупространство в декартовой системе координат задается линейным неравенством
$$
Ax+By+Cz+D \geq 0.\nonumber
$$
Обратно, любое такое неравенство можно записать как \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\), откуда сразу видно, что оно задает полупространство.

Плоскость \(P\) и вектор \(\boldsymbol{n}_{1} =-\boldsymbol{n}\) задают другое полупространство с уравнением \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}_{1}) \geq 0\) или \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \leq 0\). Его назовем “отрицательным”, в отличие от “положительного” полупространства \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Однако такое наименование условно — оно определяется выбором вектора \(\boldsymbol{n}\). Изменение направления этого вектора равносильно умножению уравнения плоскости на (—1). При этом “положительное” полупространство становится “отрицательным”, и наоборот.

Вот, однако, факт, не зависящий от выбора направления нормального вектора: если \(M_{1}(x_{1}, y_{1}, z_{1})\) и \(M_{2}(x_{2}, y_{2}, z_{2})\) две точки, не лежащие в плоскости, то результаты подстановки их координат в левую часть уравнения плоскости \(Ax_{1}+By_{1}+Cz_{1}+D\) и \(Ax_{2}+By_{2}+Cz_{2}+D\) имеют один знак тогда и только тогда, когда точки лежат в одном полупространстве.

Для решения задач бывает полезно следующее замечание: если точка \(M_{0}(x_{0}, y_{0}, z_{0})\) лежит на плоскости, то точка с координатами \(x_{0}+A\), \(y_{0}+B\), \(z_{0}+C\) лежит в “положительном” полупространстве. Иначе говоря, вектор с координатами \(A, B, C\) направлен в “положительное” полупространство. Это легко проверяется подстановкой.

Вполне аналогично сказанному о полупространствах мы можем определить, что такое полуплоскость, и доказать, что неравенство \(Ax+By+Cz+D \geq 0\), связывающее декартовы координаты точки на плоскости, определяет полуплоскость. Вторая полуплоскость, ограниченная прямой \(Ax+By+C=0\), задается неравенством \(Ax+By+C \leq 0\).

Точки \(M_{1}(x_{1}, y_{1})\) и \(M_{2}(x_{2}, y_{2})\) лежат по одну сторону от прямой тогда и только тогда, когда \((Ax_{1}+By_{1}+C)(Ax_{2}+By_{2}+C) > 0\).

4.2. Способ вращения

Сущность способа вращения состоит в том, что положение системы плоскостей проекций считается неизменным в пространстве, а положение проецируемого объекта относительно неподвижных плоскостей изменяется.

Из сравнения сущности обоих способов видно, что решение задач, которые требуют применения преобразования ортогонального чертежа, может быть выполнено любым из этих способов, результат при этом должен получиться одинаковым. Основа выбора того или иного способа – рациональность решения.

Вращение заданных элементов будем осуществлять вокруг проецирующей прямой, то есть прямой, перпендикулярной какой-либо плоскости проекций, при этом все точки заданных элементов поворачиваются в одну и ту же сторону на один и тот же угол (Рисунок 4.4, а и б). Ось вращения и объект вращения составляют твёрдое тело.

А – точка в пространстве;

О – центр вращения точки А;

АО – радиус вращения

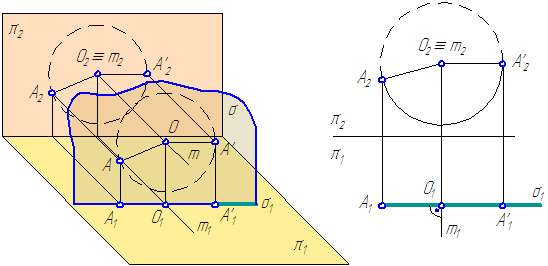
Рисунок 4.4 – Способ вращения вокруг прямой, перпендикулярной π₂

Точка описывает в пространстве окружность радиусом АО. Плоскость окружности перпендикулярна оси вращения (σ⊥m).

Так как m⊥π₂ , то σ//π₂, следовательно, σ⊥π₁, ⇒ σ₁⊥m₁, и поэтому σ проецируется на π₁ в виде прямой, перпендикулярной проекции оси вращения, а на π₂ траектория вращающейся точки проецируется в виде окружности с центром О₂≡m₂.

Пусть ось вращения m⊥π₁ (Рисунок 4.5, а и б). Плоскость окружности σ⊥m.

₁

Примеры задач по уравнению плоскости

Чтобы ещё лучше понять вышеописанную тему, необходимо решить много задач. Поэтому предлагаем вам ознакомиться с примерами и их решениями.

Составление уравнения плоскости

Пример

Задача

Даны точки и . Составить уравнение плоскости, которая проходит через точку  и перпендикулярна к вектору .

Решение

По условию вектор – это нормальный вектор плоскости. Найдём его координаты.

= .

Подставляя в уравнение (1) , а также

У нас получается:

Составление уравнения в отрезках

Пример

Задача

Построить плоскость и записать её уравнение в отрезках, а также уравнение следов на соответствующих координатных плоскостях.

Решение:

Положим , тогда . Аналогично при находим , при , , тогда уравнение в отрезках запишется:

(рис. 7)

Рис. 7

Уравнение следов:

Уравнение плоскости через три точки

Пример

Задача

Составить уравнение и построить плоскость, которая проходит через точки

Решение

По формуле (4)

Плоскость параллельна (рис.

Рис. 8

Вычисление угла между плоскостями

Пример

Задача

Найти угол между плоскостями и

Решение

Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:

= = = =

Вы заметили, что в этом примере мы воспользовались исключительно одной формулой? В нашем случае – (5) формула. Никаких других формул мы не использовали и смогли найти угол между двумя плоскостями.

Вычисление углов.

Чтобы найти угол между двумя прямыми, следует найти их направляющие векторы и вычислить косинус угла между ними, используя скалярное произведение. При этом следует иметь в виду, что, изменив направление одного из векторов, мы получим косинус смежного угла.

Для нахождения угла между прямой и плоскостью определяют угол \(\theta\) между направляющим вектором прямой и нормальным вектором плоскости. Если векторы выбрать так, чтобы \(\cos \theta \geq 0\), и взять \(0 \leq \theta \leq \pi/2\), то искомый угол дополняет \(\theta\) до \(\pi/2\).

Угол между плоскостями находят как угол между их нормальными векторами.

Полезна бывает формула для угла между прямыми линиями на плоскости, заданными уравнениями \(y=k_{1}x+b_{1}\) и \(y=k_{2}x+b_{2}\) декартовой прямоугольной системе координат. Обозначим через \(\varphi\) угол между прямыми, отсчитываемый от первой прямой ко второй в том же направлении, в котором производится кратчайший поворот от первого базисного вектора ко второму. Тогда \(\operatorname{tg} \varphi\) можно найти как тангенс разности углов, которые прямые составляют с осью абсцисс. Так как тангенсы этих углов равны угловым коэффициентам прямых, мы получаем
$$
\operatorname{tg} \varphi=\frac{k_{2}-k_{1}}{1+k_{1}k_{2}}.\label{ref10}
$$

Рис. 7.4. \(\varphi=\varphi_{2}-\varphi_{2}\)

Конечно, эта формула не имеет смысла, когда знаменатель дроби обращается в нуль. В этом случае прямые перпендикулярны. Действительно, векторы с компонентами \(1, k_{1}\) и \(1, k_{2}\) — направляющие векторы прямых, и их скалярное произведение равно \(1+k_{1}k_{2}\). Таким образом, верно следующее утверждение.

Утверждение 2.

Для перпендикулярности прямых с угловыми коэффициентами \(k_{1}\) и \(k_{2}\) в декартовой прямоугольной системе координат необходимо и достаточно выполнение равенства \(1+k_{1}k_{2}=0\).

1.3. Варианты задания 1

Таблица 1– Значения координат точек

Вариант	Координаты (x, y, z) точек
А	В	С	D
1	15; 55; 50	10; 35; 5	20; 10; 30	70; 50; 40
2	80; 65; 50	50; 10; 55	10; 50; 25	75; 25; 0
3	95; 45; 60	130; 40; 50	40; 5; 25	80; 30; 5
4	115; 10; 0	130; 40; 40	40; 5; 25	80; 30; 5
5	55; 5; 60	85; 45; 60	100; 5; 30	50; 25; 10
6	55; 5; 60	70; 40; 20	30; 30; 35	30; 10; 10
7	60; 10; 45	80; 45; 5	35; 0; 15	10; 0; 45
8	5; 0; 0	35; 0; 25	20; 0; 55	40; 40; 0
9	50; 5; 45	65; 30; 10	30; 25; 55	20; 0; 20
10	60; 50; 35	40; 30; 0	30; 15; 30	80; 5; 20
11	65; 35; 15	50; 0; 30	20; 25; 25	5; 0; 10
12	75; 65; 50	45; 10; 35	60; 20; 10	10; 65; 0
13	95; 0; 15	85; 50; 10	10; 10; 10	55; 10; 45
14	45; 40; 40	80; 50; 10	10; 10; 10	55; 10; 45
15	80; 20; 30	55; 30; 60	15; 10; 20	70; 65; 30
16	75; 35; 35	55; 30; 60	25; 10; 20	70; 65; 30
17	75; 65; 50	45; 5; 55	5; 45; 10	70; 20; 0
18	65; 15; 20	40; 5; 60	0; 5; 25	60; 60; 20
19	70; 20; 10	45; 15; 60	5; 10; 20	60; 65; 10
20	20; 50; 45	10; 20; 10	55; 50; 10	80; 0; 60
21	0; 5; 50	50; 50; 40	5; 55; 10	45; 5; 0
22	55; 50; 65	45; 55; 5	0; 10; 45	70; 0; 40
23	65; 5; 15	40; 60; 10	0; 20; 5	60; 20; 60
24	50; 20; 45	45; 60; 30	5; 20; 10	60; 30; 5
25	55; 15; 40	40; 50; 25	5; 15; 10	50; 40; 10
26	15; 45; 40	10; 25; 5	20; 10; 30	65; 40; 35
27	70; 30; 30	55; 30; 60	20; 5; 15	65; 60; 25
28	90; 0; 15	80; 45; 10	10; 10; 10	50; 10; 45
29	110; 10; 0	120; 35; 30	35; 5; 20	70; 20; 5
30	45; 40; 40	80; 45; 10	10; 10; 10	55; 10; 40

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Математические термины

 Для начала введём некоторые определения.

Определения

Расстояние между точками – это измерение отрезка, находящегося между этими точками, составляющего длину расстояния.

Эти отрезки располагаются в определенном масштабе, потому как необходимо знать единицу длины для их измерения, без этого нельзя.

Функция – это связь величин, выражаемая в зависимости одной переменной Y, от второй переменной X.

Произвольная функция (точка) – это такая точка, которую можно расположить в любом месте.

Координатная прямая – это прямая, на которой изображают точку отсчёта 0 и единичные отрезки. Прямой также задают направление.

Действительные числа – это совокупность рациональных и иррациональных чисел.

Рациональное число – это такое число, которое может находиться в виде обыкновенной дроби, в отличие от иррационального числа.

Иррациональное число – это бесконечная непериодическая десятичная дробь. Такое число нельзя представить в виде обыкновенной дроби.

Модуль или же абсолютная величина – это обязательно неотрицательное число, которое является расстоянием определённых точек.

Задачи для самостоятельного решения

1. ЗадачаНайдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (2, 5), а также B (6, 4).
2. ЗадачаНайдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (1, 6), а также B (1, 25).
3. ЗадачаНайдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (1, -3, 4), а также B (4, 1, 4).
4. ЗадачаНайдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, -2, 7), а также B (6, 2, 5).

Ответы с решением:

1. Решение первой задачиДля решения понадобится формула:|AB| = √(xB – xA)² + (yB – yA)².Далее подставляем числа:|AB| = √(6 – 2)² + (4 – 5)² = √4² + (–1)² = √16 + 1 = √17.Ответ: |AB| равен √17.
2. Решение второй задачиФормула для нахождения:|AB| = √(xB – xA)² + (yB – yA)².Подставляем:|AB| = √(1 – 1)² + (25 – 6)² = √(0)² + (19)² = √0 + 361 = √361 = 19Ответ: |AB| равен 19.
3. Решение третьей задачиЗапишем формулу:√(xB – xA)² + (yB – yA)² + (zB – zA)².Подставим числа:√(4 – 1)² + (1 – (–3))² + (4 – 4)² = √(3)² + (4)² + (0)² = √9 + 16 + 0 = √25 = 5.Ответ: |AB| равняется 5.
4. Решение четвертой задачиЗаписываем формулу для решения:√(xB – xA)² + (yB – yA)² + (zB – zA)²Заменим на координаты точек:√(6 – 2)² + (2 – (–2))² + (5 – 7)² = √(4)² + (4)² + (–2)² = √16 + 16 + 4= √36 = 6.Ответ: |AB| равняется 6.

Как определить расстояние между двумя точками на плоскости

Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.

Из этого можно вывести несколько вариантов:

Ось Ox

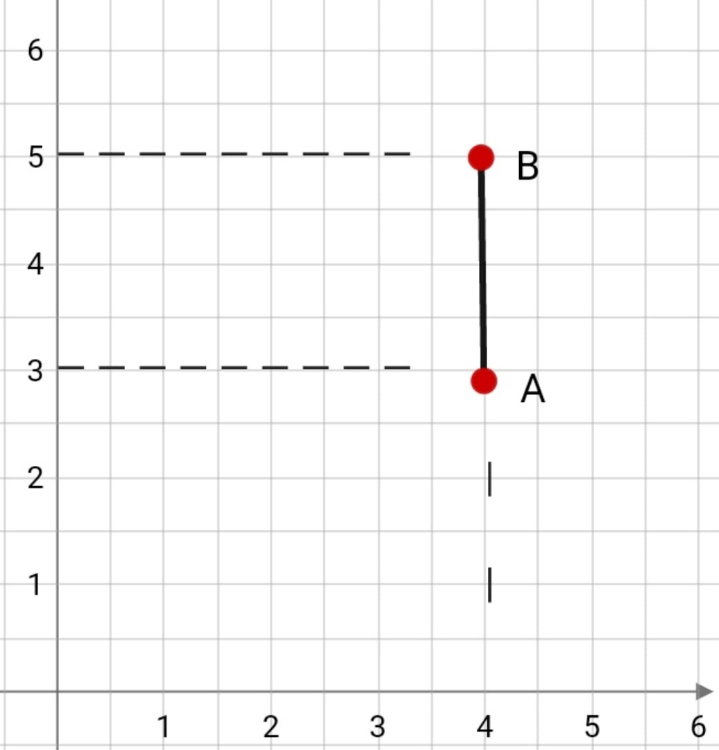
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:

|AB| = |AyBy| = |yB – yA|.

При этом совпадении их расстояние равняется 0.

Формула

Формула для нахождения расстояния между двумя точками на плоскости:

Ось Oy

Теперь рассмотрим тот случай, когда прямая перпендикулярна оси Oy. Находится расстояние таким же образом, но уже с участием xB и xA: |AB| = |AxBx| = |xB – xA|.

Формула

Формула для нахождения расстояния между двумя точками на плоскости:

Точки не лежат на прямой, которая перпендикулярна оси Ox и Oy

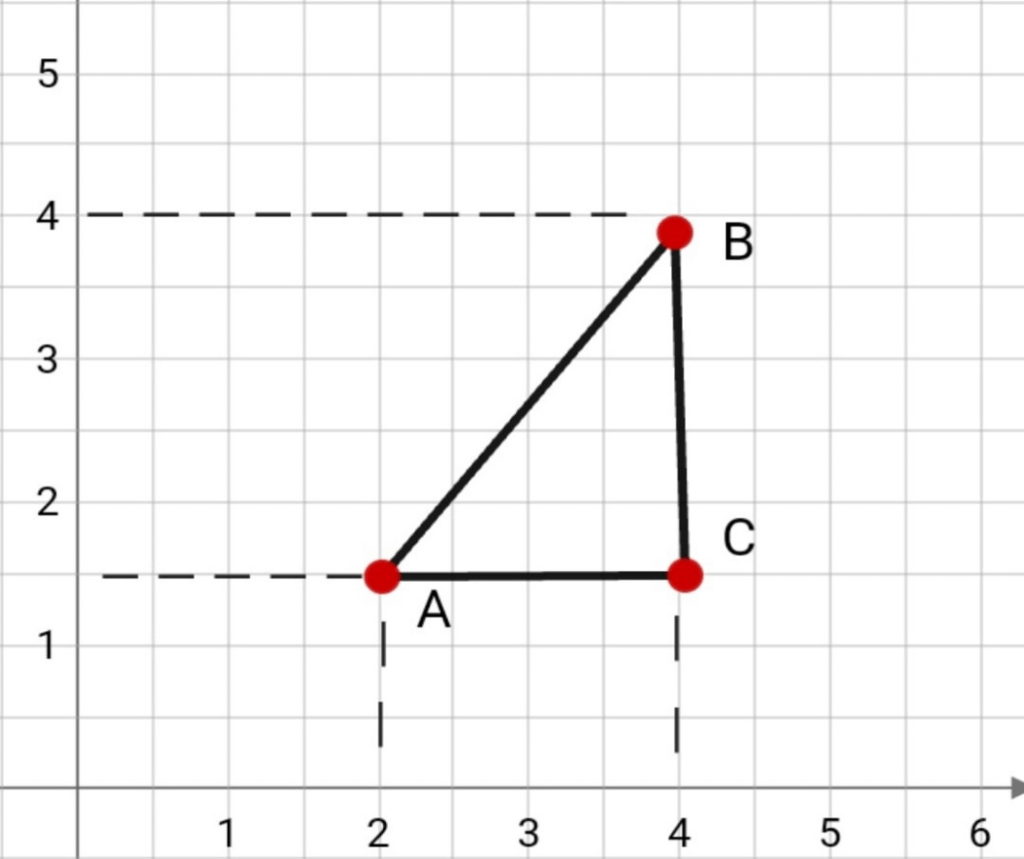
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:

|AB| = √(xB – xA)² + (yB – yA)².

 Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.

Если точки совпадают, к ним справедливо равенство:

|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.

По рисунку видно, что:

|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:

|AB|² = |AC|² + |BC|²

|AB|² = |AxBx|² + |AyBy|²

√|AxBx|² + |AyBy|²

√|xB – xA|² + |yB – yA|²

√(xB – xA)² + (yB – yA)²

Пример

Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7). Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.

Чтобы решить эту задачу, необходимо использовать формулу:

|AB| = √(xB – xA)² + (yB – yA)².

После этого действия подставляем вышеприведённые числа:

√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.

Далее обратим внимание на то, что |AB| = 10 и составим равенство:

√X² + 64 = 10

X² + 64 = 100

X = ± 6

Ответ: |AB| = 10, при X = ±6.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

4.1. Способ перемены плоскостей проекций

Чаще всего геометрические объекты расположены относительно плоскостей проекций в общем положении, и при решении задач для достижения поставленной цели необходимо выполнять много построений.

Количество построений можно значительно сократить, если геометрические элементы будут расположены в частном положении относительно плоскостей проекций.

Существуют два основных способа преобразования чертежа, при которых:

1. Объект остаётся неподвижным, при этом меняется аппарат проецирования;
2. Условия проецирования не меняются, но изменяется положение объекта в пространстве.

К первому способу относится способ перемены плоскостей проекций.

Ко второму – способ вращения (вращение вокруг линии уровня и вращение вокруг проецирующей прямой); способ плоскопараллельного перемещения.

Рассмотрим наиболее часто используемые способы при решении задач.

Способ перемены плоскостей проекций или способ введения дополнительных плоскостей проекций (ДПП) позволяет перейти от заданной системы плоскостей проекций к новой системе, более удобной для решения той или иной задачи.

Рассмотрим положение точки А относительно известной системы плоскостей проекций π₂⊥π₁ (Рисунок 4.1, а и б).

Введём π₄⊥π₁, при этом получим новую систему двух взаимно перпендикулярных плоскостей. Положение точки А на эпюре будет в этом случае задано проекциями А₁ и А₄.

Правила перемены плоскостей проекций:

1. Новая плоскость проекций вводится перпендикулярно, по крайней мере, одной из заданных на чертеже плоскостей проекций;
2. ДПП располагается относительно проецируемого объекта в частном положении, удобном для решения поставленной задачи;
3. Новую плоскость совмещаем вращением вокруг новой оси проекций с плоскостью, которой она перпендикулярна на свободное место так, чтобы проекции не накладывались друг на друга.

Рисунок 4.1 – Способ перемены плоскостей проекций

1. На чертеже новая проекция геометрического элемента находится на линии связи, перпендикулярной новой оси проекций:

1. Расстояние от А₄ до π₁/π₄ равно расстоянию от А₂ до π₂/π₁, так как величина этих отрезков (отмечены ○) определяет расстояние от точки А до плоскости проекций π₁.

При решении задачи необходимо заранее обдумать, как расположить новую плоскость проекций относительно заданных геометрических объектов (прямой, плоскости и др.), и как на чертеже провести новую ось проекций, чтобы в новой системе плоскостей заданные объекты заняли бы частные положения по отношению к новой плоскости проекций.

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением $$ \Phi(x,y)=0 \ . $$ Здесь $ \Phi_(x,y) $ — отличный от константы полином от $ x_ $ и $ y_ $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ \mathbb R^ $.

Будем решать задачу сначала для частного случая — пусть полином $ \Phi_(x,y) $ является четным по переменной $ y_ $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ \mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) \equiv \Phi_(x,y) \quad npu \quad Y=y^2 \ . $$

Теорема 1 . Пусть $ \Phi_(x,y) \equiv \Phi_(x,-y) $. Уравнение $ \Phi_(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ \Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение $$ \mathcal F(z)=\mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ \Phi(x_,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ \Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ \mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ _ $ — дискриминант полинома, рассматриваемого относительно переменной $ x_ $.

Пример. Найти расстояние от начала координат до кривой

Решение. Уравнение $$ \Phi(x,0)=x^6-6\,x^5+25\,x-45=0 $$ имеет вещественные корни $ \mu_1\approx -1.621919 $ и $ \mu_2 \approx 5.986387 $.

задача о трёх заводах.

Пример. В точках $ P_,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ $ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.

Задача о точке Лемуана-Греба

Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_ $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)\equiv $$ $$ \equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 \ . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_ $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S \ , $$ где $ S_ $ — площадь данного треугольника. Следовательно $ \min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0,\ d_2D_3-d_3D_2=0,\ d_1D_3-d_3D_1=0 \ , $$ то есть когда $$ \frac=\frac=\frac\ . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.