Общее уравнение плоскости

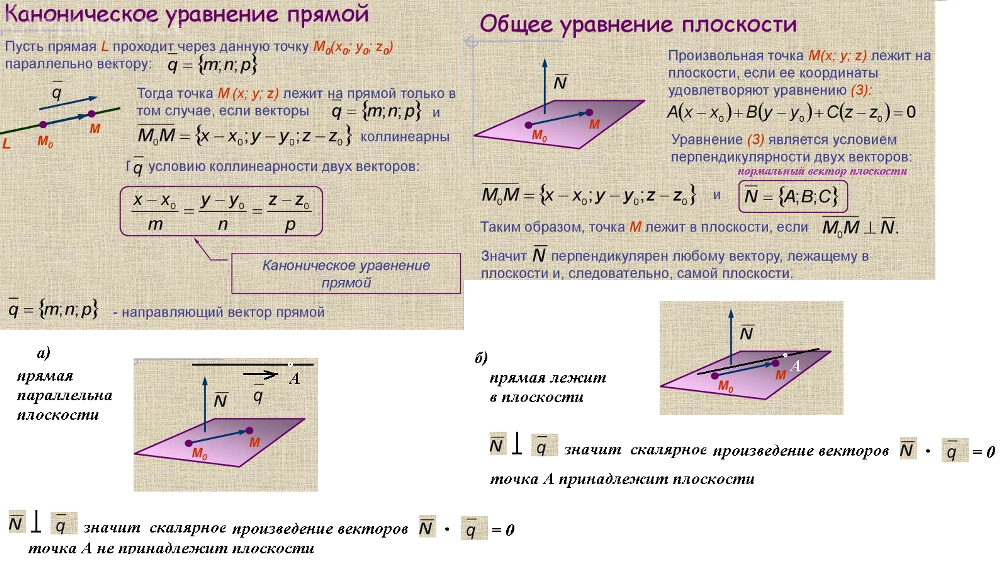
Уравнение плоскости и его компоненты

Уравнение плоскости — это алгебраическое уравнение, которое описывает геометрическое положение каждой точки плоскости относительно ее положения в пространстве. Оно имеет следующий вид: Ax + By + Cz + D = 0. Здесь A, B и C — коэффициенты уравнения, а D — свободный член, который определяет расстояние плоскости от начала координат.

Коэффициенты A, B и C называются компонентами нормали плоскости и определяют ее направление. Нормаль к плоскости — это вектор, перпендикулярный этой плоскости. Его координаты соответствуют компонентам A, B и C уравнения плоскости. Если нормальный вектор плоскости известен, то уравнение плоскости можно записать в виде Ax + By + Cz + D = 0, где коэффициенты A, B и C равны компонентам нормали, а D определяется координатами одной из точек на плоскости.

Свободный член D может быть определен различными способами, например, как расстояние от плоскости до начала координат, как расстояние от плоскости до определенного ориентира или как координата любой точки на плоскости. Если известна точка на плоскости и нормальный вектор, то D можно найти, решив уравнение для этой точки. В таком случае получаем: D = -(Ax + By + Cz).

Использование уравнения плоскости позволяет решать различные задачи, связанные с геометрическим положением точек, прямых и плоскостей в пространстве. Это может быть построение пересечения плоскостей, нахождение расстояния от точки до плоскости, а также применение в задачах на геометрию и физику.

Примеры применения плоскости в реальной жизни

Плоскость — геометрическая фигура, которая является ровной и бесконечной во всех направлениях. Она играет важную роль в различных сферах нашей жизни. Вот несколько примеров, где мы можем наблюдать применение плоскости:

1. Архитектура: Плоскость является одной из основных конструктивных составляющих в строительстве. Она используется в создании стен, полов, крыш и других элементов зданий. Архитекторы и инженеры полагаются на плоскость, чтобы создавать привлекательные и функциональные конструкции.
2. География: Глобус Земли может быть представлен как плоская поверхность, так как на картах и атласах топография мира изображается на плоской поверхности. Это позволяет нам изучать распределение земных масс и формировать представление о разных регионах мира.
3. Искусство и дизайн: Многие художники используют плоскость в своих произведениях, чтобы создавать разнообразные эффекты и перспективу. Они могут использовать плоскость, чтобы создать иллюзию глубины или выделить определенные элементы в своих работах.
4. Транспорт: Воздушные и морские карты используют плоскость для определения маршрутов и навигации. Водители и пилоты также используют карты, которые представлены на плоской поверхности, чтобы определить свое местоположение и планировать свои перемещения.
5. Наука и инженерия: Плоскость играет важную роль в различных ветвях науки и инженерии, таких как математика, физика и геометрия. Она используется для проведения экспериментов, моделирования и анализа данных.

Применение плоскости в реальной жизни весьма широко и разнообразно. Она является неотъемлемой частью многих областей и помогает нам лучше понять и визуализировать окружающий мир.

Примеры задач на работу с плоскостью в пространстве

1. Найти угол между двумя плоскостями: $2x — 3y + 4z = 5$ и $5x + 4y — z = 1$. Для решения этой задачи нужно найти нормальные векторы каждой плоскости и использовать формулу для нахождения косинуса угла между векторами.

2. Определить, проходит ли прямая $x = 2 + t, y = -1 — 3t, z = 3 + 2t$ через плоскость $3x — 2y + z = 7$. Для решения этой задачи необходимо подставить координаты точки прямой в уравнение плоскости и проверить, выполняется ли равенство.

3. Найти координаты точки пересечения плоскостей $2x — y + 3z = 4$ и $3x + 2y — 5z = 1$. Для решения этой задачи можно использовать метод Гаусса, который позволяет привести систему уравнений к удобному для решения виду.

4. Определить, параллельны ли плоскости $x — 2y + 3z = 4$ и $2x — 4y + 6z = 8$. Для решения этой задачи нужно найти нормальные векторы каждой плоскости и проверить, равны ли они или противоположны по направлению.

5. Найти уравнение плоскости, проходящей через точки $A(1,2,3)$, $B(2,-1,4)$ и $C(-1,3,5)$. Для решения этой задачи необходимо найти векторное произведение векторов, соответствующих сторонам треугольника $ABC$, и подставить его в уравнение плоскости.

6. Найти расстояние от точки $M(2,-1,3)$ до плоскости $2x — y + 3z = 4$. Для решения этой задачи можно использовать формулу для нахождения расстояния между точкой и плоскостью.

Задачи на работу с плоскостью в пространстве могут быть разнообразны и довольно сложными, но решение каждой из них требует применения конкретных математических методов и формул.
Для успешного решения задач на работу с плоскостью в пространстве необходимо иметь навыки работы с векторами, уметь находить координаты точек и выполнять алгебраические операции.
При решении задач на работу с плоскостью в пространстве особое внимание нужно уделять правильному считыванию условия задачи и выбору необходимого математического метода для ее решения.

Линии на плоскости: прямые и кривые

В пространстве, которое является плоскостью, существуют различные типы линий — прямые и кривые. Линии играют важную роль в геометрии и математике в целом, а также применяются в различных областях науки и техники.

Прямые — это элементарные линии, которые не имеют изгибов и можно задать двумя разными точками. Они простираются бесконечно в обе стороны и не имеют ширины. Прямые могут быть вертикальными, горизонтальными или наклонными.

Кривые — это линии, которые могут иметь изгибы и изменения кривизны в разных частях. Они могут быть заданы уравнениями, параметрическими уравнениями или иными способами. Кривые могут быть закрытыми, то есть образовывать замкнутые фигуры, или незакрытыми.

Существует множество различных типов прямых и кривых на плоскости. Некоторые из наиболее распространенных включают:

• Прямая — простая линия, которая соединяет две точки и не имеет изгибов.
• Отрезок — часть прямой, ограниченная двумя конечными точками.
• Полуоткрытый интервал — линейный график, который идет от одной конечной точки до бесконечности, исключая эту конечную точку.
• Полузакрытый интервал — линейный график, который идет от одной конечной точки до бесконечности, включая эту конечную точку.

1. Эллипс — кривая, которая представляет собой замкнутый овал.
2. Парабола — кривая, которая открывается вверх или вниз и является симметричной.
3. Гипербола — кривая, которая состоит из двух ветвей и является симметричной.

Линии на плоскости имеют важное значение не только в геометрии, но и в различных областях применения, таких как инженерия, физика, компьютерная графика и многое другое. Понимание различных типов линий помогает в решении задач и анализе фигур на плоскости

Уравнение для плоскости, которая проходит через 3 точки

Если 3-мерном пространстве дана прямоугольная к-ная система, она обозначена обычно Oxyz.

Тогда уравнение, где данные a, b и C являются действительными числами больше нуля, именуется ур-ем плоскости на отрезки.

При абсолютном значении чисел a, b и с, они будут равны длине отрезков, обрезанных плоскостью по осям координат. Буквенные значения демонстрируют положительное или отрицательное направление линейных сегментов относительно оси координат.

Чтобы составить общее уравнение для исходной плоскости, можно применить следующую теорему.

Теорема:

Любое уравнение, имеющее стандартный вид, имеет действительные значения A, b, C и D, которые не должны быть равны нулю. Эти данные определяют исходную плоскость в системе координат Oxyz, расположенной в 3-мерном пространстве.

Эта теорема содержит в себе 2 части:

1. Сначала получаем общее уравнение для плоскости, которая будет проходить через точку и саму плоскость.
2.  Затем мы доказываем, что данное уравнение можно использовать для действительных чисел, чтобы доказать, что оно будет определять плоскость V, Z и D.

Доказательство 1 части:

1. Так как значения чисел A, V и Z не будут равны нулю одновременно, значит есть определенная точка, координаты которой будут соответствовать исходному уравнению, то есть выдавать верное равенство. 
2. Далее вычитаем правую и левую части полученного уравнения из данного уравнения. Получается уравнение, которое будет эквивалентно исходному.  
3. Далее необходимо будет доказать, что полученное уравнение будет определять именно плоскость в данной системе координат 3-мерного пространства и найти общее уравнение.

Главным условием для перпендикулярности 2 векторов является их равенство. То есть, когда координаты удовлетворяют уравнению, то векторы будут перпендикулярны и наоборот. При верном равенстве набор точек будет обуславливать плоскость, проходящую через эту точку.

Полученное уравнение будет определять плоскость, расположенную в 3-мерном пространстве. Также оно будет полностью соответствовать для общего уравнения плоскости, которая проходит через три точки.

Из сказанного следует, что любое уравнение, эквивалентное исходному, будет определять одну и ту же плоскость. Мы доказали 1 часть теоремы.

Доказательство 2 части теоремы:

Когда имеем плоскость, проходящую через точку, вектор которой нормален, мы можем доказать, что в прям-ной координатной системе Oxyz ее задают с помощью данного основного уравнения.

Если взять любую точку данной системы координат, то векторы будут перпендикулярны, а произведение будет равно нулю.

 После принятия данного понятия, уравнение снова изменится и будет определять нашу плоскость.

Вывод: если уравнения эквивалентны, то они определяют одинаковую плоскость. Мы доказали теорему.

Данный обзор будет полезен при решении математических задач, а также в аналитической геометрии.

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

Составляем определитель и приравниваем его к нулю:

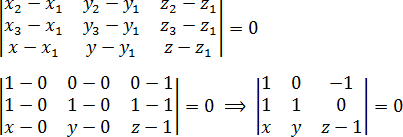
Раскрываем определитель:

a
= 1 · 1 · (z
− 1) + 0 · 0 · x
+ (−1) · 1 · y
= z
− 1 − y;b
= (−1) · 1 · x
+ 0 · 1 · (z
− 1) + 1 · 0 · y
= −x;d
= a
− b
= z
− 1 − y
− (−x
) = z
− 1 − y
+ x
= x
− y
+ z
− 1;d
= 0 ⇒ x
− y
+ z
− 1 = 0;

Как видите, при расчете числа d
я немного «причесал» уравнение, чтобы переменные x
, y
и z
шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a
= 1 · 1 · z
+ 0 · 1 · x
+ 1 · 0 · y
= z;b
= 1 · 1 · x
+ 0 · 0 · z
+ 1 · 1 · y
= x
+ y;d
= a
− b
= z
− (x
+ y
) = z
− x
− y;d
= 0 ⇒ z
− x
− y
= 0 ⇒ x
+ y
− z
= 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x
2 или x
3 , а в какой — просто x
. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax
+ By
+ Cz
+ D
= 0. Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.

Параметрические уравнения прямой и плоскости.

Прямая линия (на плоскости или в пространстве) полностью определена, если на ней задана точка \(M_{0}\) и задан ненулевой вектор \(\boldsymbol{a}\), параллельный этой прямой. Разумеется, и точку, и вектор можно выбрать по-разному, но мы будем считать, что они как-то выбраны, и называть их начальной точкой и направляющим вектором. Аналогично, плоскость задается точкой и двумя неколлинеарными векторами, ей параллельными, — начальной точкой и направляющими векторами плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Пусть дана прямая. Обозначим через \(\boldsymbol{r}_{0}\) и \(\boldsymbol{a}\) соответственно радиус-вектор ее начальной точки \(M_{0}\) и направляющий вектор. Рассмотрим некоторую точку \(M\) с радиус-вектором \(\boldsymbol{r}\) (рис. 6.1).

Рис. 6.1

Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t\boldsymbol{a}.\label{ref3}
$$

Наоборот, какое бы число мы ни подставили в формулу \eqref{ref3} в качестве \(t\), вектор \(\boldsymbol{r}\) в этой формуле определит некоторую точку на прямой.

Уравнение \eqref{ref3} называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Рассмотрим прямую в пространстве. Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\), соответственно, а вектор \(\boldsymbol{a}\) имеет компоненты \((a_{1}, a_{2}, a_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref3}, мы получим
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t,\ z-z_{0} = a_{3}t.\label{ref4}
$$
Для прямой на плоскости мы получаем, аналогично,
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t.\label{ref5}
$$
Уравнения \eqref{ref4} или \eqref{ref5} называются параметрическими уравнениями прямой.

Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol{p}\) и \(\boldsymbol{q}\) ее направляющие векторы, а через \(\boldsymbol{r}_{0}\) — радиус-вектор ее начальной точки \(M_{0}\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol{r}\) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol{p}\) и \(\boldsymbol{q}\) не коллинеарны, в этом и только этом случае \(\boldsymbol{r}-\boldsymbol{r}_{0}\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_{1}\) и \(t_{2}\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t_{1}\boldsymbol{p}+t_{2}\boldsymbol{q}.\label{ref6}
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_{1}\) и \(t_{2}\). Наоборот, какие бы числа мы ни подставили как значения \(t_{1}\) и \(t_{2}\), уравнение \eqref{ref6} определит некоторую точку плоскости.

Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\) соответственно, а векторы \(\boldsymbol{p}\) и \(\boldsymbol{q}\) имеют компоненты \((p_{1}, p_{2}, p_{3})\) и \((q_{1}, q_{2}, q_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref6}, мы получим параметрические уравнения плоскости
$$
x-x_{0} = t_{1}p_{1}+t_{2}q_{1},\ y-y_{0} = t_{1}p_{2}+t_{2}q_{2},\ z-z_{0} = t_{1}p_{3}+t_{2}q_{3}.\label{ref7}
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Способы задания плоскости

	Способ 1. Плоскость однозначно определена, если указана точка, лежащая в этой плоскости, и вектор (направленный отрезок), перпендикулярный этой плоскости.
•                                     •                 •	Способ 2. Плоскость однозначно определена, если указаны три точки, лежащие в этой плоскости.
	Способ 3. Плоскость однозначно определена, если указаны точка, лежащая в этой плоскости, и два неколлинеарных вектора, параллельных этой плоскости.

6.2.Уравнения плоскости

Выберем в пространстве декартову прямоугольную систему
координат с базисом . В некоторых случаях,
вместо термина «система координат» удобнее применять термин «репер»

Определение 6.1. Репером или системой координат в
пространстве называют
упорядоченный набор , состоящий из
зафиксированной точки пространства , называемой началом
координат, и базиса пространства.

Каждая точка  определяет
вектор =,
приложенный к началу координат. Координатами вектора = являются координаты точки . Вектор  называют
радиус-вектором точки  . Любая пара точек
  и определяет
вектор =,
координатами которого являются разности координат точек  и
: =.

Пусть = —
точка и вектор в этом пространстве. Они однозначно определяют плоскость , проходящую через точку  и перпендикулярную вектору .
Пусть также — любая точка, лежащая в плоскости , не совпадающая с . Отрезок ,
а значит и вектор перпендикулярны вектору . Следовательно, скалярное
произведение векторов  и  равно
нулю:

==0.

Переобозначим: .
Тогда координаты любой точки, лежащей в плоскости , удовлетворяют
равенству:

(6.1)

В то же время, если точка не лежит в плоскости , то ее координаты не удовлетворяют
равенству (6.1). Равенство (6.1) называют уравнением плоскости,
проходящей через заданную точку, перпендикулярно заданному вектору.

Раскроем скобки в уравнении (6.1) и обозначим число . Равенство (6.1) примет вид:

(6.2)

которое
называют общим уравнение плоскости.

Геометрический смысл коэффициентов в уравнении (6.2) очевиден: то
координаты известного вектора нормали к плоскости =(). Выясним геометрический смысл
свободного члена уравнения, числа . Найдем =,
то есть вектор сонаправленный  и имеющий
единичную длину (см. стр  ). =(), причем =1
или . Чтобы нормировать вектор , надо его координаты (), разделить на его длину, то есть на
число . Получим:

 =()=.

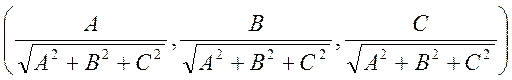Разделим уравнение (6.2) на длину вектора :

(6.3)

где
. Уравнение (6.3) называют нормированным
уравнением плоскости.

Рассмотрим вектор =(). При любом  он
коллинеарен вектору , его начало совпадает с
началом координат. Подберем  таким, чтобы
конец вектора  лежал на плоскости. Тогда — это расстояние от начала координат
до плоскости. Концом искомого вектора является точка, координаты которой
удовлетворяют уравнению (6.3):

.

Обозначим
расстояние от начала координат до плоскости .
Тогда =  при
, то есть:  

 .

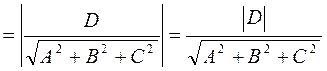(6.4)

Итак, абсолютная величина свободного члена в
общем уравнении плоскости есть произведение расстояния от начала координат до
плоскости на длину ее нормального вектора. Если уравнение плоскости
нормировано, то абсолютная величина свободного члена есть расстояние от начала
координат до плоскости.

Пусть заданы три точки,
 и .Эти
точки однозначно определяют плоскость, в которой они
лежат. Пусть также — любая точка, лежащая в плоскости
, не совпадающая ни с одной из точек ,  или
. Векторы ,
 и  компланарны.
Следовательно, их смешанное произведение ()
равно нулю (см. стр.  ), то есть справедливо равенство:

=0,

(6.5)

которое
называют уравнением плоскости, проходящей через три заданные точки.

Пользуясь свойствами
определителей, представим определитель в равенстве (6.5) в виде суммы двух
определителей:

=+.

Первой строкой определителя  являются
переменные ,  и
. Разложив его по первой строке,
получим:

=—

—+

+=,

где
 — коэффициенты перед переменными,
полученные в результате вычислений. Обозначим число, полученное в результате
вычисления определителя  через .

После этих преобразований, уравнение плоскости,
проходящей через три заданные точки, примет вид общего уравнения плоскости: .

Плоскость однозначно определена, если указаны точка,
лежащая в этой плоскости, и два неколлинеарных вектора, параллельных этой
плоскости. Пусть — точка, лежащая в
плоскости , = и = — два неколлинеарных друг другу
вектора, причем оба параллельны плоскости .
Векторное произведение векторов  и

Определение плоскости в математике

Плоскость – это геометрическая фигура в трехмерном пространстве, которая представляет собой бесконечную плоскую поверхность. Плоскость не имеет толщины и состоит из бесконечно маленьких точек, расположенных на одной и той же высоте.

Плоскость может быть определена с помощью различных характеристик:

1. Точка и нормаль. Плоскость может быть определена одной точкой и вектором нормали, который перпендикулярен плоскости и указывает на ее направление.
2. Три точки. Плоскость может быть определена, если даны три точки, не лежащие на одной прямой. В этом случае плоскость проходит через эти три точки и содержит все возможные точки, лежащие на прямых, соединяющих эти точки.
3. Уравнение плоскости. Плоскость может быть определена с помощью уравнения вида Ax + By + Cz + D = 0, где A, B и C – коэффициенты, которые определяют нормаль плоскости, а D – константа.

Плоскость в математике имеет ряд свойств:

• Любые две точки, лежащие на плоскости, можно соединить прямой, которая полностью лежит на этой плоскости.
• Плоскость делит трехмерное пространство на две половины – верхнюю и нижнюю. Все точки в одной половине находятся на одной стороне плоскости, а все точки в другой половине – на другой стороне.
• Плоскость может пересекаться с другими плоскостями, образуя линию, которая называется прямой пересечения.

Примеры плоскостей:

1. Плоскость, параллельная горизонтальной плоскости земли. Например, поверхность озера или моря.
2. Поверхность стола или доски, на которых мы пишем или кладем предметы.
3. Стены в комнате считаются плоскостями, хотя они имеют толщину, но по сравнению с их длиной и шириной толщина пренебрежимо мала.
4. Экран компьютера или телевизора также является плоскостью.

Плоскость является одной из основных концепций в геометрии и широко применяется в различных областях, таких как инженерия, физика и компьютерная графика.

Что такое плоскость в математике: определение и свойства

Плоскость — одно из основных понятий в геометрии. Она является двумерным аналогом пространства и представляет собой бесконечное множество точек, расположенных в плоскости без толщины. В математике плоскость обычно обозначается буквой P.

Плоскость можно определить как геометрическое место точек, удовлетворяющих определенным условиям. Например, плоскость может быть определена как множество точек, находящихся на одинаковом расстоянии от заданной точки — центра плоскости. Данное определение позволяет рассматривать плоскость как плоское зеркало, отражающее свет и формирующее визуальное отображение объектов.

У плоскости есть несколько характеристик и свойств:

• Бесконечность: плоскость не имеет границ и простирается бесконечно во всех направлениях.
• Двумерность: плоскость имеет только две измерения — длину и ширину. Она не имеет высоты и не имеет объема.
• Параллельность: две плоскости называются параллельными, если они не пересекаются и не имеют общих точек.
• Взаимное расположение: плоскости могут быть перпендикулярными, если они пересекаются под прямым углом.
• Прямые на плоскости: плоскость содержит бесконечное множество прямых, которые могут быть расположены в любом направлении.

Плоскости являются важным инструментом в геометрии и используются для моделирования и анализа различных объектов. Они помогают описывать пространственные отношения, расстояния, углы и другие геометрические характеристики.

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2

Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T
= (x
; y
; z
) в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные x
, y
и z
, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

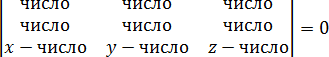
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax
+ By
+ Cz
+ D
= 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Итак, рассматриваем 4 точки:

B
1 = (1, 0, 1);
C = (1, 1, 0);D
1 = (0, 1, 1);T
= (x
, y
, z
).

Для начала составим стандартный определитель и приравниваем его к нулю:

Раскрываем определитель:

a
= 0 · 1 · (z
− 1) + 1 · 0 · (x
− 1) + (−1) · (−1) · y
= 0 + 0 + y;b
= (−1) · 1 · (x
− 1) + 1 · (−1) · (z
− 1) + 0 · 0 · y
= 1 − x
+ 1 − z
= 2 − x
− z;d
= a
− b
= y
− (2 − x
− z
) = y
− 2 + x
+ z
= x
+ y
+ z
− 2;d
= 0 ⇒ x
+ y
+ z
− 2 = 0;

Все, мы получили ответ: x
+ y
+ z
− 2 = 0 .

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x
, y
, z
не внизу, а вверху:

Вновь раскрываем полученный определитель:

a
= (x
− 1) · 1 · (−1) + (z
− 1) · (−1) · 1 + y
· 0 · 0 = 1 − x
+ 1 − z
= 2 − x
− z;b
= (z
− 1) · 1 · 0 + y
· (−1) · (−1) + (x
− 1) · 1 · 0 = y;d
= a
− b
= 2 − x
− z
− y;d
= 0 ⇒ 2 − x
− y
− z
= 0 ⇒ x
+ y
+ z
− 2 = 0;

Мы получили точно такое же уравнение плоскости: x
+ y
+ z
− 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку B
1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D
1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Yandex.RTB R-A-339285-1

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Теорема 1

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А, В, С и D
– некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А, В, С
и D
конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число

Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Пример 1

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А, B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Пример 2

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А, В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости. Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости

Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.