Векторная алгебра — примеры с решением заданий и выполнением задач

Ортогональные векторы и условие ортогональности: определение, примеры решения задач

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a¯ и b¯, угол между которыми равен 900.

Необходимое условие для ортогональности векторов — два вектора a¯ и b¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

a¯ × b¯=0

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a¯={ax×ay} и b¯={bx×by} записывают следующим образом:

a¯×b¯=ax×bx + ay×by=0

Задача 1.  Докажем, что векторы a¯={1;2} и b¯={2;-1} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)=2-2=0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a¯={3;-1} и b¯={7;5} ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=3×7+(-1)×5=21-5=16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n, при котором векторы a¯={2;4} и b¯={n;1} будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a¯×b¯=2×n+4×1=2n+42n+4=02n=-4n=-2

Ответ: векторы являются ортогональными при значении n=2.

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a¯={1;2;0} и b¯={2;-1;10} условие записывается следующим образом: a¯×b¯=ax×bx+ay×by+az×bz=0.

Задача 4. Докажем, что векторы a¯={1;2;0} и b¯={2;-1;10} являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=1×2+2×(-1)+0×10=2-2=0

Ответ: поскольку произведение векторов  равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n, при котором векторы a¯={2;4;1} и b¯={n;1;-8} будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a¯×b¯=2×n+4×1+1×(-8)=2n+4-8=2n-42n-4=02n=4n=2

Ответ: векторы a¯ и b¯ будут ортогональными при значении n=2.

Решение задач
от 1 дня / от 150 р.

Преподаватель математики и информатики.

2 Вектор на плоскости и в пространстве

Вектором
называется направленный отрезок с началом и концом, изображаемым на
рисунке стрелкой. Произвольная точка пространства может считаться
нулевым вектором. Нулевой вектор не имеет конкретного направления,
так как начало и конец совпадают, поэтому ему можно придать любое
направление.

Длина
(модуль) ненулевого вектора

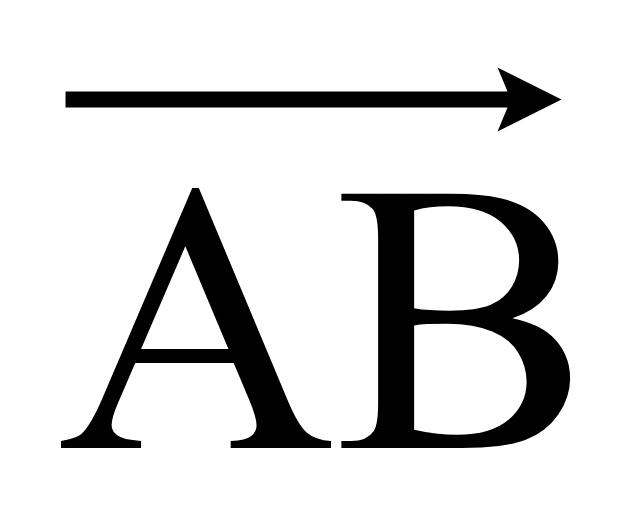
— это длина отрезка AB, которая
обозначается

.
Длина вектора

обозначается

.
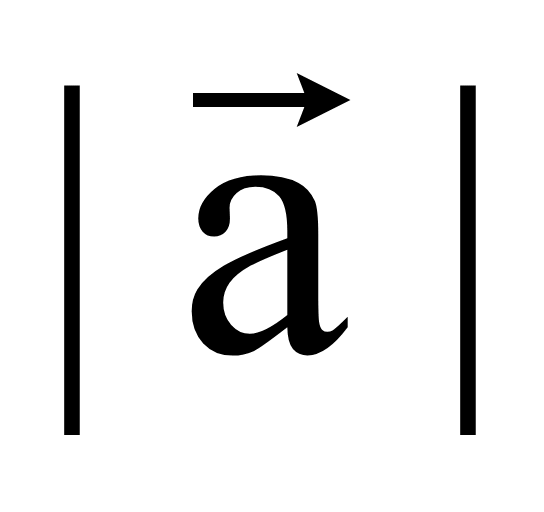
Нулевой вектор имеет длину равную нулю

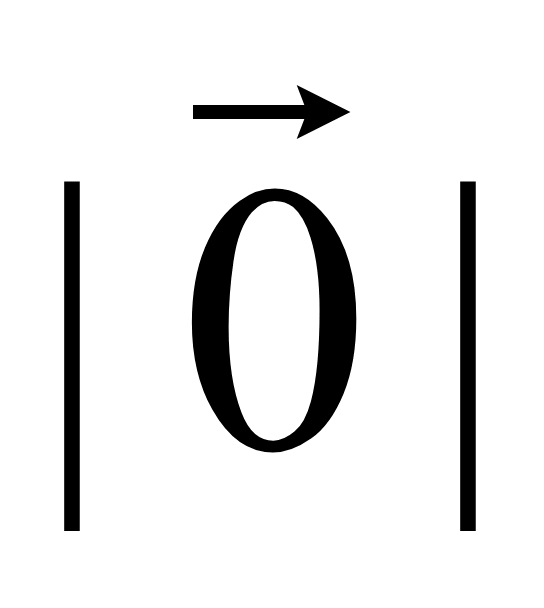
= 0.

Коллинеарными
называются ненулевые векторы, лежащие на одной прямой или на
параллельных прямых. На рисунках ниже изображены коллинеарные векторы

,

.

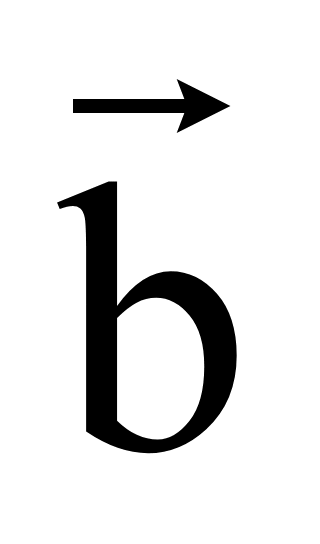
На
рисунке ниже также изображены коллинеарные векторы

,
и
.

Нулевой
вектор коллинеарен любому вектору.

Нулевой
вектор сонаправлен с любым вектором.

Равными
называются сонаправленные векторы равной длины. На рисунке ниже
изображены равные векторы

=
.

Противоположными
называются два ненулевых противоположно направленных вектора равной
длины. Вектор —

является противоположным вектору

Противоположные
векторы противоположно направленные и равны по модулю. Если даны
точки A и B,
то следующие векторы противоположные

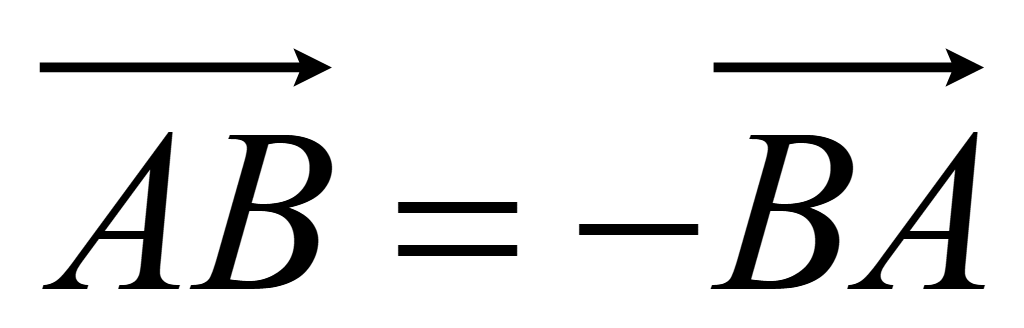
Равные
по модулю равные или противоположные, или нулевые векторы.

Многие
физические величины являются векторными величинами: сила, скорость,
электрическое поле и т.д.

Если
не задана точка приложения (начала) вектора, то она выбирается
произвольно.

Если
в точку O поместить начало вектора, то
считается, что вектор отложен от точки O.
Из любой точки можно отложить единственный вектор, равный данному
вектору.

Определитель третьего порядка

Отныне и впредь, когда ты будешь иметь дело с методом координат на плоскости, тебе очень часто будут встречаться эти самые определители.

Что же такое определитель третьего порядка? Как ни странно, это всего-навсего число. Осталось понять, какое конкретно число мы будем сопоставлять с определителем.

Давай вначале запишем определитель третьего порядка в более общем виде:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right|\),Где \( {{a}_{ij}}\) – некоторые числа.

Причем под первым индеком \( \displaystyle i\) мы понимаем номер строки, а под индеком \( \displaystyle j\) – номер столбца.

Например, \( {{a}_{23}}\) означает, что данное число стоит на пересечении второй строки и третьего столбца.

Давай поставим следующий вопрос: каким именно образом мы будем вычислять такой определитель?

То есть, какое конкретно число мы будем ему сопоставлять?

Для определителя именно третьего порядка есть эвристическое (наглядное) правило треугольника оно выглядит следующим образом:

Как его читать? А понимать его надо следующим образом: мы составляем два выражения:

• Произведение элементов главной диагонали (с верхнего левого угла до нижнего правого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» главной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» главной диагонали;
• Произведение элементов побочной диагонали (с верхнего правого угла до нижнего левого) \( \displaystyle +\) произведение элементов, образующих первый треугольник «перпендикулярный» побочной диагонали \( \displaystyle +\) произведение элементов, образующих второй треугольник «перпендикулярный» побочной диагонали;
• Тогда определитель равен разности значений, полученных на шаге \( \displaystyle 1\) и \( \displaystyle 2\).

Если записать все это цифрами, то мы получим следующее выражение:

\( \left| {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}} \right| = \)\( = {a_{11}}{a_{22}}{a_{33}} + {a_{12}}{a_{23}}{a_{31}} + {a_{21}}{a_{32}}{a_{13}} — \left( {{a_{13}}{a_{22}}{a_{31}} + {a_{23}}{a_{32}}{a_{11}} + {a_{21}}{a_{12}}{a_{33}}} \right)\)Тем не менее, запоминать способ вычисления в таком виде не нужно, достаточно в голове просто держать треугольники и саму идею, что с чем складывается и что из чего затем вычитается).

7 Компланарные векторы

Компланарными
называются векторы, лежащие в одной плоскости или в параллельных
плоскостях. Если провести векторы, равные данным компланарным
векторам из одной точки, то они будут лежать в одной плоскости.
Поэтому можно сказать, что компланарными называются векторы, если
имеются равные им векторы, лежащие в одной плоскости.

Два
произвольных вектора всегда компланарны потому что всегда можно
подобрать две параллельные плоскости, в которых будут лежать эти
векторы. Три вектора могут быть компланарными или не компланарными.
Три вектора, из которых хотя бы два коллинеарные, всегда компланарны.
Коллинеарные векторы всегда компланарны.

Выбор системы координат

Ну вот, теперь у нас есть весь необходимый фундамент знаний, чтобы решать сложные стереометрические задачи по геометрии.

Однако прежде чем приступать непосредственно к примерам и алгоритмам их решения, я считаю, что будет полезно остановиться еще вот на каком вопросе: как именно выбирать систему координат для той или иной фигуры.

Ведь именно выбор взаимного расположения системы координат и фигуры в пространстве в конечном счете определит, насколько громоздкими будут вычисления.

Я напомню, что в этом разделе мы рассматриваем следующие фигуры:

• куб;
• Прямоугольный параллелепипед;
• Прямая призма (треугольная, шестиугольная…);
• Пирамида (треугольная, четырехугольная);
• Тетраэдр (одно и то же, что и треугольная пирамида).

Евклидовы пространства

Скалярное произведение

Евклидовым пространством называется линейное вещественное пространство V,
в котором задано отображение V × V —> R, ставящее каждой паре векторов
x, y ∈ V число (x, y) ∈ R,
называемое скалярным произведением.

Скалярное произведение обладает следующими свойствами:

1. (x, y) = (y, x),
2. (x + y, z) = (x, z) + (y, z),
3. (αx, y) = α(x, y),
4. x ≠ 0 => (x, x) > 0

Скалярное произведение в евклидовом пространстве есть положительно определенная симметричная билинейная функция.
И наоборот, любую положительно определенную симметричную функцию можно выбрать в качестве скалярного произведения (см.
методичку uic.unn.ru).
Про билинейные функции читайте здесь.

Матрица Грама

Квадратная симметрическая матрица G(e₁, e₂, . . ., e_n),
составленная из скалярных произведений системы векторов e₁, e₂, . . ., e_n
называется матрицей Грама.

Т.е. матрица Грама выглядит так:

G(e₁, e₂, . . ., e_n) =

(e1, e1)	(e1, e2)	. . .	(e1, en)
(e2, e1)	(e2, e2)	. . .	(e2, en)
. . .	. . .	. . .	. . .
(en, e1)	(en, e2)	. . .	(en, en)

Матрицу Грама можно представить как произведение матрицы A, составленной из координат
некоторой системы векторов, и её транспонированной версии:G(e₁, e₂, . . ., e_n) = A * AT

Матрица Грама имеет большое прикладное значение. Она может быть использована для выяснения линейной зависимости системы векторов;
нахождения объёма n-мерного параллелепипеда, построенного на этих векторах; вычисления расстояния от конца вектора до некоторого
подпространства векторов (и угла между вектором и подпространством) (подробнее см.
mathhelpplanet.com).

Можно также вывести формулу изменения матрицы Грама при переходе от одного базиса e₁, e₂, . . ., e_n
к другому базису e’₁, e’₂, . . ., e’_n:
G(e’₁, e’₂, . . ., e’_n) = ST * G(e₁, e₂, . . ., e_n) * S

Где матрица S является переходной от базиса e₁, e₂, . . ., e_n к
базису e’₁, e’₂, . . ., e’_n.

Матрица Грама позволяет записать выражение скалярного произведения через координаты векторов
(в базисе e₁, e₂, . . ., e_n):
(x, y) = xT * G(e₁, e₂, . . ., e_n) * y
    (1)

Матрицы Грама ортонормированных базисов единичные.

Определитель матрицы G(e₁, e₂, . . ., e_n)
называется определителем Грама. Он имеет несколько полезных свойств.

Во-первых, именно с помощью определителя Грама можно выявить линейную независимость системы векторов:
система векторов v₁, v₂, . . ., v_nлинейно
зависима тогда и только тогда, когда определитель Грама этой системы равен нулю:
det G(v₁, v₂, . . ., v_n) = 0

Также ещё говорят, что система векторов линейно зависима, когда матрица Грама положительно полуопределена
(см. критерий Сильвестра в предыдущем разделе).
Это более широкая по смыслу трактовка первого свойства определителя Грама.

Во-вторых, определитель Грама det G(v₁, v₂, . . ., v_n) не изменяется
в процессе v₁, v₂, . . ., v_n.

Кроме этого, определитель Грама векторов v₁, v₂, . . ., v_n
равен квадрату n-мерного объема параллелепипеда, построенного на этих векторах.
В этом заключается геометрический смысл определителя Грама
(читайте подробнее тут:
mathhelpplanet.com). То есть:
det G(v₁, v₂, . . ., v_n) = V2_{v1, v2, . . ., vn}

Нахождение вектора, перпендикулярного данному.

Значительную ценность представляет умение находить координаты вектора, перпендикулярного заданному вектору. Покажем как это делается на плоскости и в пространстве с использованием условия перпендикулярности векторов в координатной форме.

Начнем с нахождения вектора, перпендикулярного данному, на плоскости.

Следует понимать, что для заданного ненулевого вектора на плоскости существует бесконечное множество перпендикулярных векторов. Покажем это. Пусть вектор лежит на прямой a. Тогда любой ненулевой вектор , лежащий на любой из прямых, перпендикулярных прямой a, будет перпендикулярен вектору . К примеру, координатному вектору перпендикулярен вектор , а также любой из векторов , где — произвольное действительное число, отличное от нуля.

Таким образом, задача нахождения координат вектора , перпендикулярного вектору на плоскости имеет бесконечное множество решений. Так как же найти координаты хоть какого-нибудь вектора, перпендикулярного вектору ?

Для этого записываем условие перпендикулярности двух векторов в координатной форме , где и — искомые координаты перпендикулярного вектора. Далее, если , то придаем координате произвольное ненулевое значение, а координату находим из равенства . Если же , а , то придаем координате произвольное значение, отличное от нуля, а координату находим как .

Пример.

Найдите какой-нибудь вектор, перпендикулярный вектору .

Решение.

Пусть искомым вектором является вектор . Найдем его координаты.

По условию перпендикулярности векторов и имеем 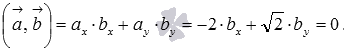. Примем , тогда , откуда . Таким образом, вектор — один из векторов, перпендикулярных вектору .

Ответ:

.

Аналогично ищется вектор, перпендикулярный заданному вектору в трехмерном пространстве.

Для вектора существует бесконечное множество перпендикулярных векторов. Покажем это. Пусть вектор лежит на прямой a. Обозначим буквой произвольную плоскость, перпендикулярную прямой a. Тогда любой ненулевой вектор , принадлежащий плоскости , перпендикулярен вектору .

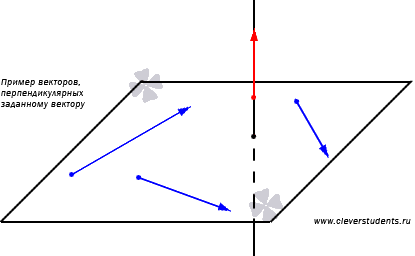
Покажем, как с помощью условия перпендикулярности векторов находятся координаты некоторого вектора , перпендикулярного данному ненулевому вектору .

Пусть вектор имеет координаты и . Найдем их.

По условию перпендикулярности двух векторов должно выполняться равенство . Так как вектор ненулевой, то хотя бы одна из его координат отлична от нуля. Пусть (можно принять или ). Тогда можно разделить на эту координату обе части равенства , при этом получим 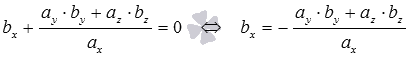. Таким образом, придав координатам и произвольные значения, хотя бы одно из которых отлично от нуля, и вычислив при этом по формуле , мы получим вектор, перпендикулярный заданному вектору .

Разберем на примере.

Пример.

Найдите координаты какого-нибудь вектора, перпендикулярного вектору .

Решение.

Пусть искомым вектором является . По условию перпендикулярности двух векторов должно выполняться условие

Примем , тогда .

Таким образом, — один из векторов, перпендикулярных вектору .

Ответ:

.

Координаты вектора на плоскости, равного по модулю и перпендикулярного данному

Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.

Алгоритм получения координат перпендикулярных векторов

Вектор на плоскости xOy, перпендикулярный данному вектору получают так:

1. Поменять местами координатные числа «x» и «y».
2. Заменить знак у одной из координат на противоположный.

Графический пример

Рассмотрим небольшой графический пример (рис. 1).

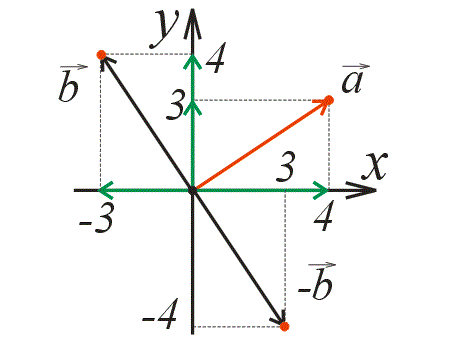
Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом

На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).

Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).

Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )

Векторы, изображенные черным цветом, перпендикулярны красному вектору.

Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.

Ортогональная матрица

Ортогональная матрица A — матрица, которая обязательно имеет
обратную матрицу A-1, которая в свою очередь
равна транспонированной матрице AT.

Иными словами:
A * A-1 = A-1 * A = A * AT = AT * A = E

Определитель ортогональной матрицы равен ± 1, что следует
из свойств определителей.

Пример. Матрица оператора поворота является частным случаем ортогональной матрицы .
При этом определитель матрицы поворота равен именно +1, что относит её к специальному
классу ортогональных матриц — к группе вращений n-мерного арифметического вещественного
пространства.

То есть оператор вращения с такой матрицей поворачивает систему векторов (либо один вектор) на заданный угол
в пространстве.

Кроме того, матрицей перехода из одного ортонормированного базиса в другой ортонормированный базис
является всегда ортогональная матрица.

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

Произведение линейных преобразований.

Доказательство  последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.

Утверждение 4.

Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.

Пусть заданы линейные преобразования \(f\) и \(g\) и выбрана система координат. Тогда координаты точки \(f(M)\) выражаются через координаты точки \(M\) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1},\ y^{*}=a_{2}x+b_{2}y+c_{2}.\label{ref8}
$$
а координаты точки \(g(f(M))\) через координаты точки \(f(M)\) формулами
$$
x^{**}=d_{1}x^{*}+e_{1}y^{*}+f_{1},\ y^{**}=d_{2}x^{*}+e_{2}y^{*}+f_{2}.\label{ref9}
$$
Подстановка равенств \eqref{ref9} в \eqref{ref8} выражает координаты g(f(M)) через координаты \(M\). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.

Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного произведение двух взаимно однозначных преобразований взаимно однозначно.

Утверждение 5.

Преобразование, обратное аффинному преобразованию, также является аффинным.

Если преобразование \(f\) записано уравнениями \eqref{ref3}, то координатная запись его обратного преобразования получается решением уравнений \eqref{ref3} относительно \(x\) и \(y\). Для того чтобы решить эти уравнения, умножим первое из них на \(b_{2}\), второе — на \(b_{1}\) и вычтем одно уравнение из другого. Мы получим \((a_{1}b_{2}-a_{2}b_{1})x=b_{2}(x^{*}-c_{1})-b_{1}(y^{*}-c_{2})\). Из условия \eqref{ref4} следует, что \(x\) — линейный многочлен от \(x^{*}\) и \(y^{*}\). Выражение для \(y\) получается аналогично.

Применения скалярного произведения векторов

Расчёт работы постоянной силы

Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная
точка перемещается прямолинейно из начала координат в конец вектора B под
действием постоянной силы F = A, образующей угол
с перемещением S = A.
Из физики известно, что работа силы F при перемещении S равна
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.

Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно
часто встречается в последующих разделах математики, особенно, аналитической геометрии.
Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный
навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и
лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?

Экономический смысл скалярного произведения векторов

В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение

выражает суммарную стоимость всех товаров x.

Назад

Листать

Вперёд>>>

Поделиться с друзьями

Начало темы «Векторы»

Продолжение темы «Векторы»

Свойства сложения

Действия с векторами во многом подобны действиям с обычными числами. Напомним, что в алгебре при прибавлении к числу нуля оно не менялось:

a + 0 = a

Аналогично и при прибавлении к вектору нулевого вектора он не изменится:

Работает ли это правило с векторами? Оказывается, что да. Убедиться в этом можно, построив параллелограмм, сторонами которого являются складываемые векторы:

Видно, что диагональ параллелограмма является суммой векторов, которые соответствуют нижней и крайней правой его стороне. Они обозначены как векторы a и b, причем в данном случае к а прибавляется b. Но одновременно эта же диагональ – это сумма векторов, которые соответствуют крайней левой и его верхней стороне. Напомним, что противоположные стороны параллелограмма равны и параллельны, поэтому они и обозначены одним вектором. В этом случае уже к b прибавляется a. Результат при этом получается одинаковый, поэтому можно записать, что

На этом примере мы увидели, как работает ещё одно правило сложения векторов, который называется правилом параллелограмма. Если есть два вектора, которые необходимо сложить, то можно отложить их от одной точки, а потом достроить получившуюся фигуру до параллелограмма.

Задание. Сложите с помощью правила параллелограмма вектора, изображенные на рисунке:

Решение. Надо всего лишь построить параллелограмм, как показано на рисунке. Его диагональ и окажется искомым вектором:

Ещё один закон, использующийся в алгебре, называется сочетательным законом, записывается он так:

Оказывается, что и при действиях с векторами он также работает, то есть справедливо соотношение:

Здесь оранжевый вектор – это сумма красного (а) и синего (b) вектора. Если к оранжевому вектору добавить зеленый (с), то получится фиолетовый вектор, который, таким образом, является суммой

Желтый вектор – это сумма синего и зеленого вектора. Видно, что фиолетовый вектор представляет собой сумму красного и желтого, то есть он представляет сумму

Складывать можно любое количество векторов. В этом случае надо последовательно прикладывать эти вектора друг к другу, выстраивая «цепочку» векторов. Например, сложение 4 векторов, показанных на рисунке, будет осуществляться следующим образом:

Этот способ сложения векторов именуют правилом многоугольника. Естественно, в силу переместительного закона вектора можно прикладывать друг к другу в разной последовательности, при этом результат будет получаться один и тот же.

Задание. Сложите, используя правило многоугольника, вектора, изображенные на рисунке. Выполните сложение двумя разными способами:

В первом случае последовательно сложим вектора a, b, c и d. Во втором случае изменим последовательность сложения. Например, сложим их в порядке d, b, c, a:

Видно, что каждый из двух способов дал один и тот же результат, что ещё раз подтверждает справедливость переместительного закона сложения векторов.

Нахождение координат вектора, перпендикулярного двум заданным векторам.

Начнем с постановки задачи.

Пусть нам требуется найти координаты вектора в трехмерном пространстве, который одновременно перпендикулярен двум не коллинеарным векторам и . Если векторы и коллинеарные, то решением задачи будет вектор, перпендикулярный одному из векторов или (о нахождении такого вектора мы говорили в предыдущем пункте).

Одно из решений такой задачи основано на использовании понятия векторного произведения векторов.

Нам известно, что векторное произведение векторов и представляет собой вектор, перпендикулярный одновременно и вектору и . Таким образом, векторное произведение является решением нашей задачи. В координатной форме оно имеет вид

Разберем на примере.

Пример.

Найдите координаты какого-нибудь вектора, перпендикулярного одновременно двум векторам и .

Решение.

Решением нашей задачи является векторное произведение заданных векторов. Найдем его (при необходимости смотрите статью вычисление определителя матрицы):

Ответ:

— один из векторов, одновременно перпендикулярный и вектору и .

Список литературы.

• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.

Некогда разбираться?

Сложение векторов

Пусть некоторый объект сначала находился в точке А, а потом переместился в точку В. Тогда его перемещение удобно обозначить с помощью вектора АВ. Далее пусть этот объект из точки В переместился в другую точку С.

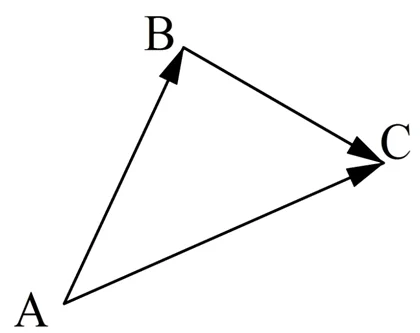
С одной точки зрения, объект совершил сразу два перемещения, из А в В и из В в С, которые можно представить векторами:

Этот пример подсказывает нам универсальное правило, с помощью которого можно складывать вектора. Его называют правилом треугольника.

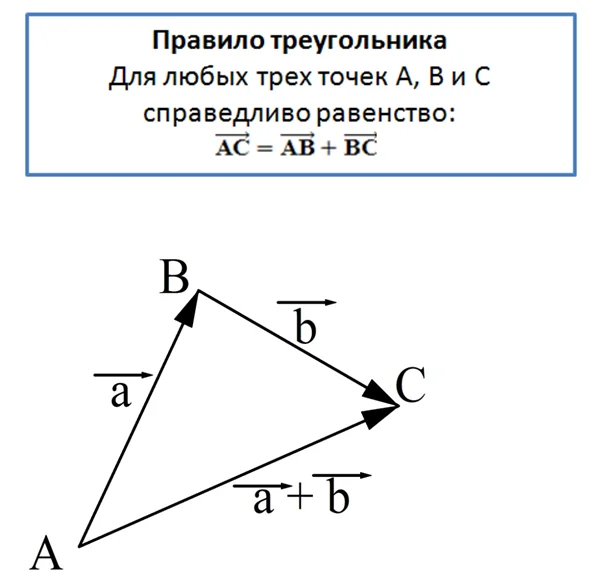
С помощью правила треугольника удобно складывать вектора, если конец одного из них совпадает с началом другого. Но что делать, если это не так? В этом случае достаточно от конца одного вектора отложить вектор, равный второму:

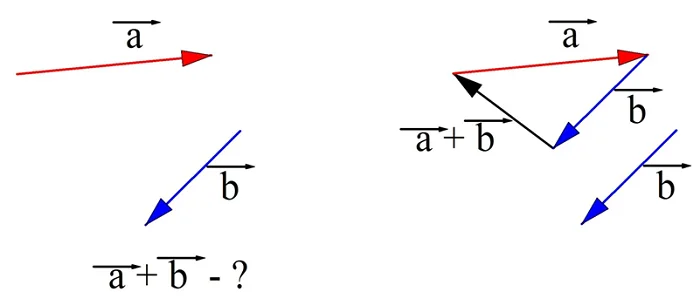
Задание. На рисунке показаны два вектора. Постройте в тетради их сумму и найдите длину получившегося вектора.

Решение. Перенесем вектор b к концу вектора а. Далее по правилу треугольника на удастся найти их сумму (обозначим этот вектор буквой с):

Теперь найдем длину получившегося вектора. Он является гипотенузой в прямоугольном треугольнике, причем длины катетов в этом треугольнике можно определить по рисунку, они составляют 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:

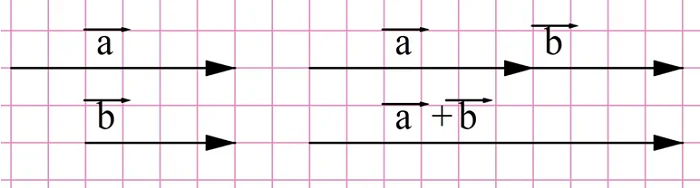
Отдельно рассмотрим случаи, когда складываются коллинеарные вектора. В этом случае получающаяся сумма окажется коллинеарной каждому слагаемому. Если вектора сонаправлены, то их длина итогового вектора окажется равной сумме длин складываемых векторов:

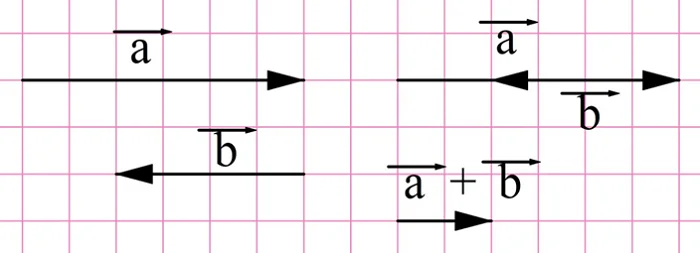
Если складываются противоположно направленные вектора, то длина их суммы окажется разностью длин складываемых векторов.

Именно по этой причине при решении простейших задач на движение корабля по реке скорость корабля и скорость течения либо складывают, либо вычитают. Дело в том, что в этих задачах складываются вектора скоростей корабля и течения. Когда судно плывет по течению, эти векторы сонаправлены, а когда плавание идет против течения, векторы оказываются противоположно направленными.

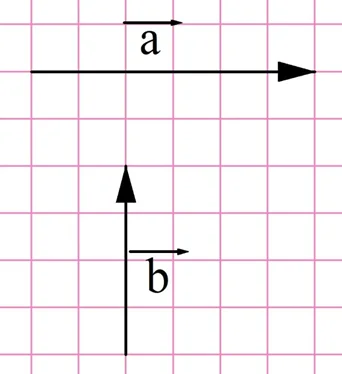
Задание. Корабль развивает в неподвижной воде скорость 12 км/ч. Он плывет по реке, скорость воды в которой составляет 5 км/ч. Найдите скорость корабля относительно берега, если:

а) судно плывет по течению;

б) судно плывет против течения;

в) судно плывет перпендикулярно течению.

Решение. Во всех случаях итоговая скорость судна является векторной суммой собственной скорости судна и течения реки:

Однако направления этих векторов различны. Найдем решение графически, с помощью построений. В первом случае вектора по условию сонаправлены:

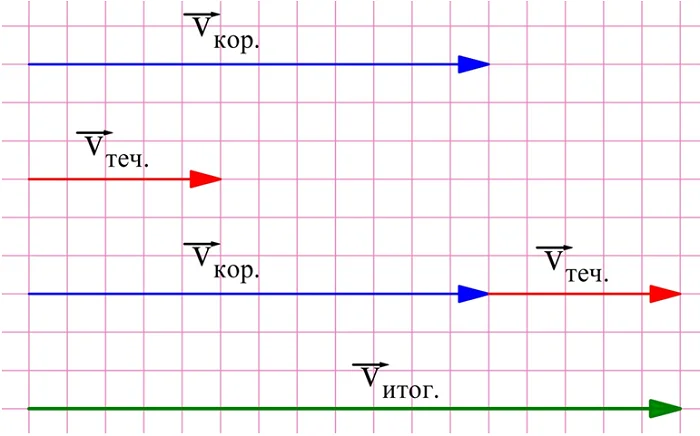
Приложив другу к другу отрезки длиной 12 и 5, получим отрезок длиной 17. Это значит, что в первом случае скорость корабля относительно берега составит 17 км/ч.

Во втором случае вектора уже окажутся противоположно направленными:

Отрезок, соответствующий итоговой скорости, здесь уже равен 7 клеткам, значит, итоговая скорость составляет 7 км/ч.

В третьем случае вектора скоростей перпендикулярны:

При построении получился прямоугольный треугольник, вектор итоговой скорости в нем оказался в роли гипотенузы. Найти его длину можно по теореме Пифагора, ведь катеты нам известны:

Вычисление углов между двумя плоскостями

Алгоритм решения будет таков:

• По трем точкам ищем уравнение первой плоскости: \( {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+{{D}_{1}}=0\)
• По другим трем точкам ищем уравнение второй плоскости: \( {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+{{D}_{2}}=0\)
• Применяем формулу: \( cos\varphi =\frac{\left| {{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}~ \right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\)

Как видишь, формула очень похожа на две предыдущие, при помощи которых мы искали углы между прямыми и между прямой и плоскостью.

Так что запомнить эту тебе не составит особого труда. Сразу переходим к разбору задач:

Матричное представление скалярного произведения векторов и произведение n-мерных векторов

Иногда выигрышным для наглядности является представление двух перемножаемых векторов
в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:

Тогда скалярное произведение векторов будет произведением этих матриц:

Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно
единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным
числом.

В матричной форме удобно представлять произведение абстрактных n-мерных векторов.
Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на
матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением
матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.

Пример 7. Найти скалярные произведения пар векторов

и

,

используя матричное представление.

Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй —
в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на
матрицу-столбец:

Аналогично представляем вторую пару и находим:

Как видим, результаты получились те же, что и у тех же пар из
примера 2.