Вектор (алгебра)

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

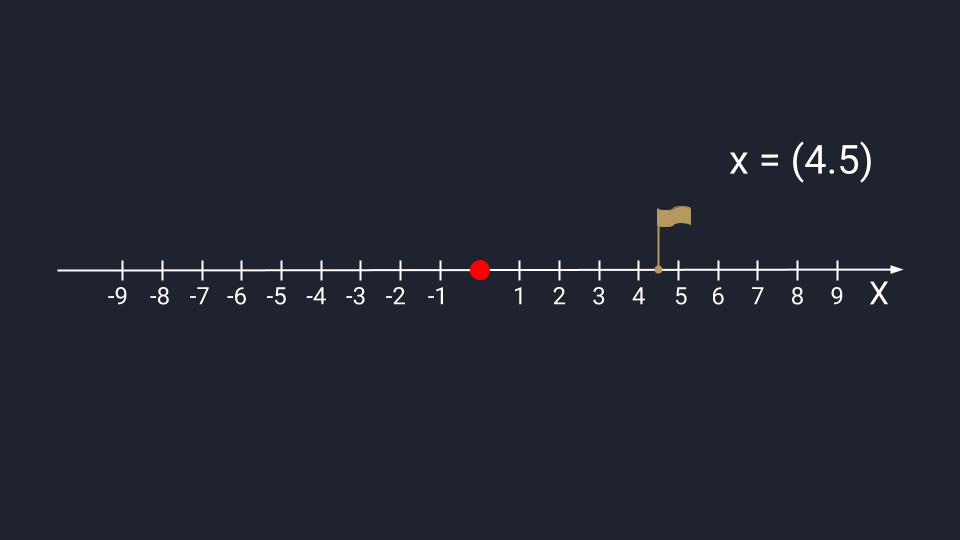Графическое представление скаляра. Записывается в круглых скобках

Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

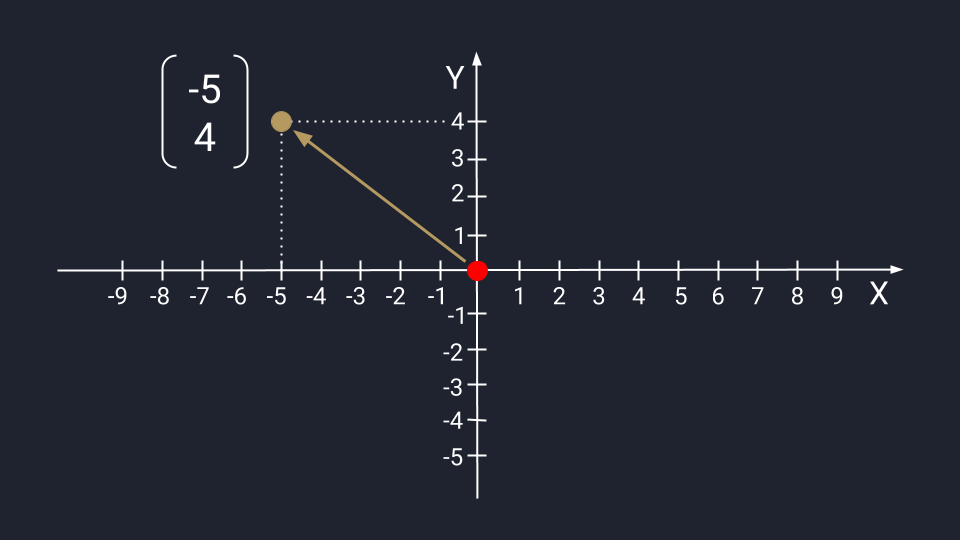Графическое представление числового вектора в двух измерениях

Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

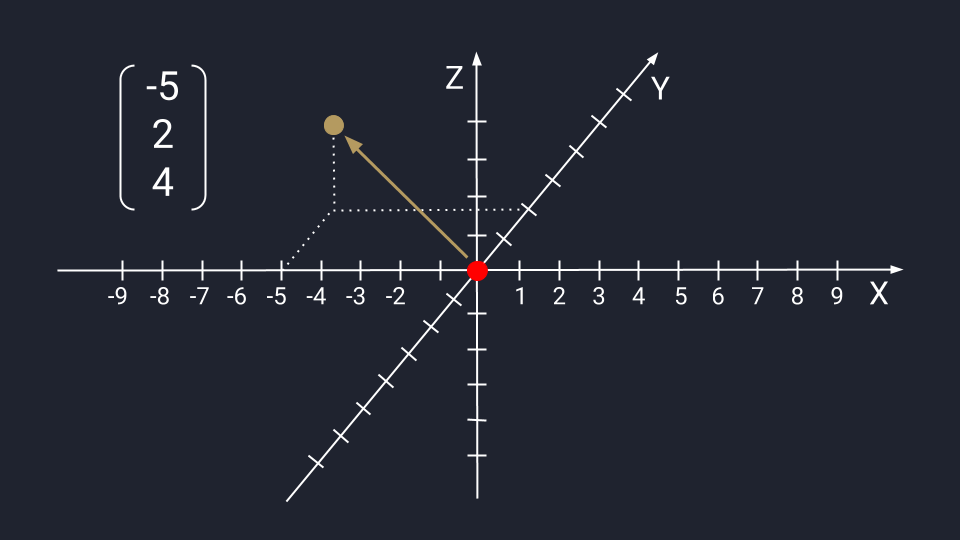Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке

Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Что такое вектор: определение, обозначение, виды

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое вектор: определение, обозначение, виды

В данной публикации мы рассмотрим, что такое вектор, как он обозначается, а также какие виды бывают.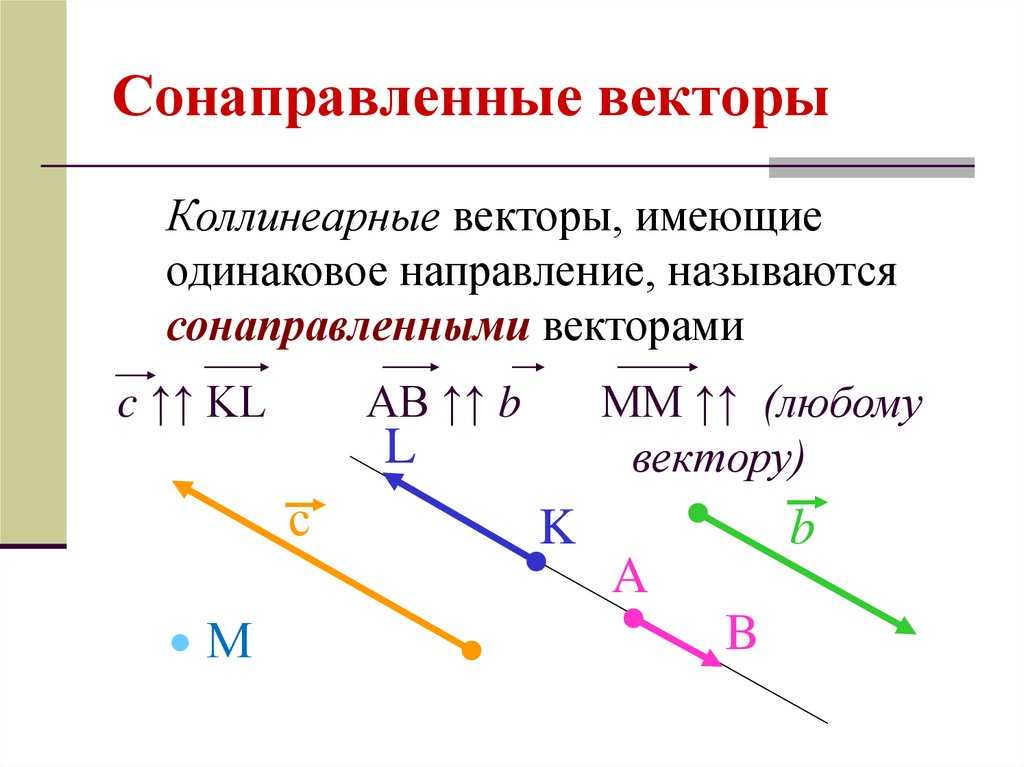

• Определение вектора
• Виды векторов

Определение вектора

Вектор – это направленный отрезок. Другими словами, это отрезок определенной длины, который направлен в конкретную сторону.

У вектора есть начало и конец. На рисунке ниже – это точки A и B, соответственно. Направление вектора показывается соответствующей стрелкой.

Обозначается вектор путем записи его точек (начало, потом – конец) с вертикальной черточкой сверху, т.е. в нашем случае – AB.

Альтернативный вариант обозначения –  малеьнкая латинская буква, например, a.

Примечание: нахождение длины вектора (|AB| или |a|) мы подробно рассмотрели в отдельной публикации.

Виды векторов

1. Нулевой – начало и конец вектора совпадают.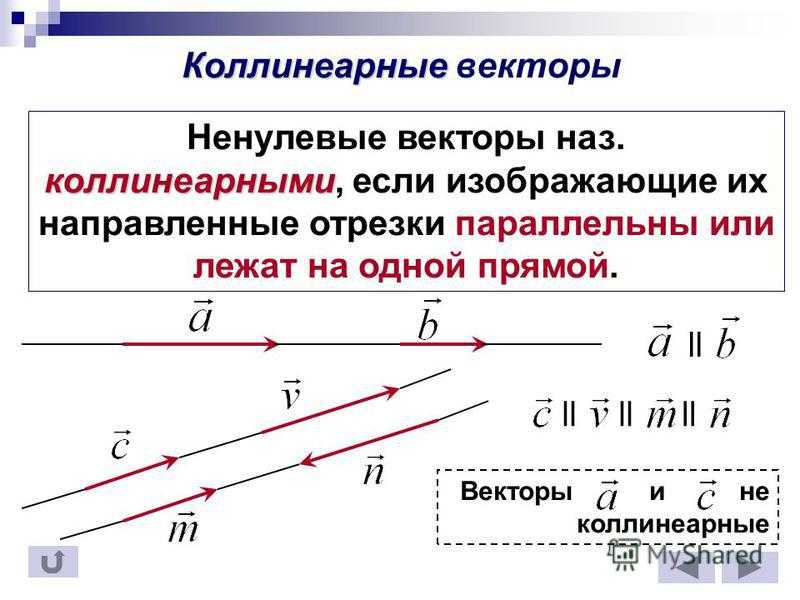

2. Единичный – вектор, длина которого равна единице. Также называется ортом.

3. Коллинеарные – векторы лежат на одной и той же или на параллельных прямых.

4. Сонаправленные – коллинеарные векторы, направления которых совпадает. Например, на рисунке ниже a и b являются сонаправленными.

5. Противоположно направленные – коллинеарные векторы, направления которых противоположны.

6. Компланарные – векторы, параллельные одной плоскости или лежащие на одной плоскости.

Примечание: любые два вектора компланарны, так как всегда найдется плоскость, параллельная им обоим.

7. Равные – векторы, имеющие одинаковую длину и направление, а также лежащие на одной или параллельных прямых.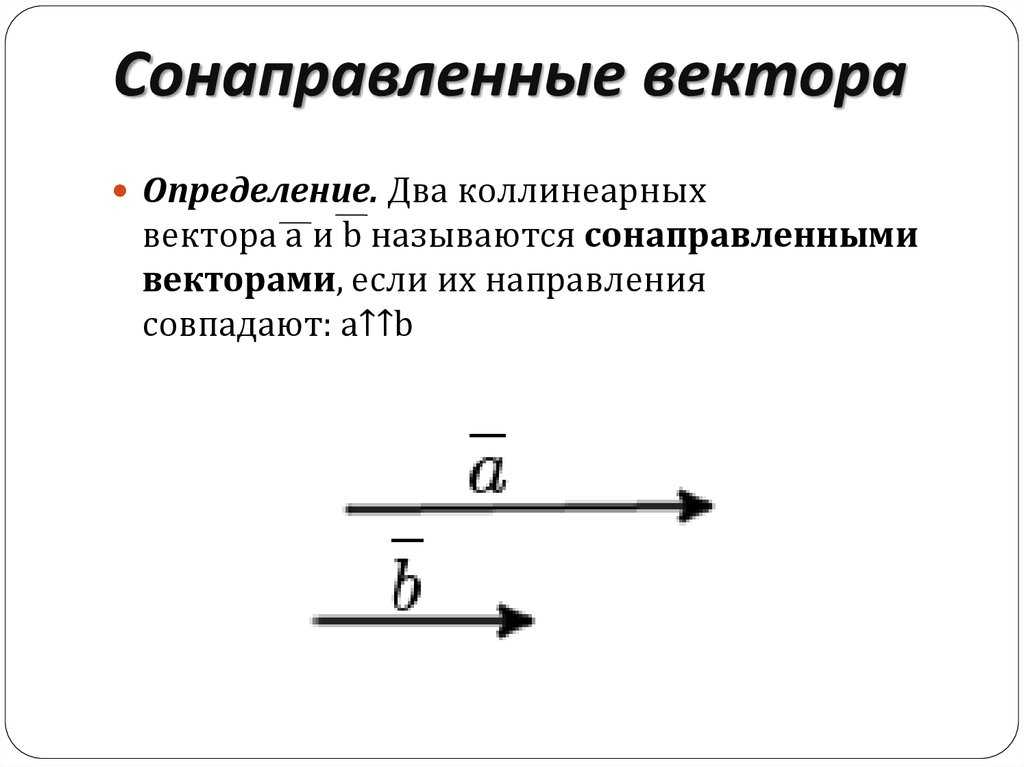

Примечание: для вектора AB в произвольной точке C пространства удастся построить только один единственный вектор (например, CD) той же длины.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

Проекция вектора — это длина отрезка, который образуется

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта

И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

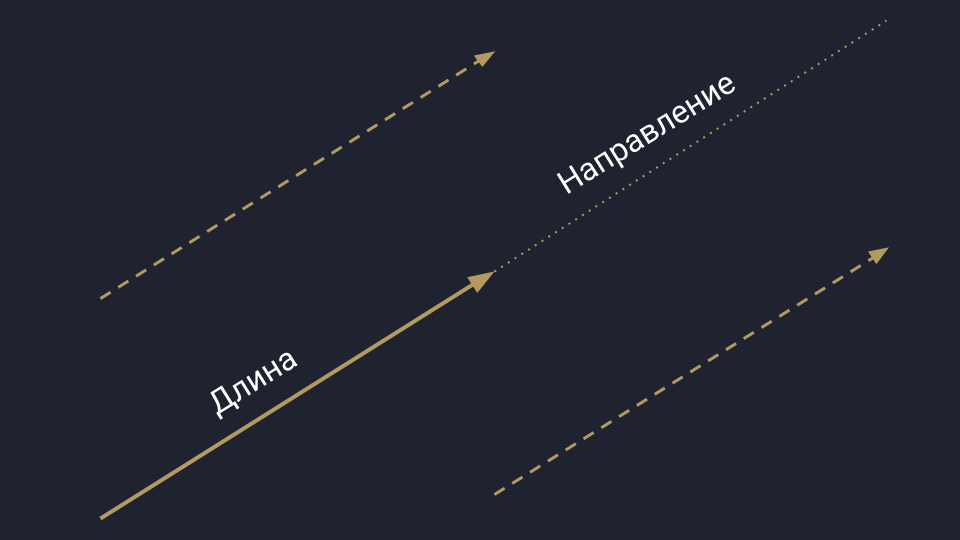Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

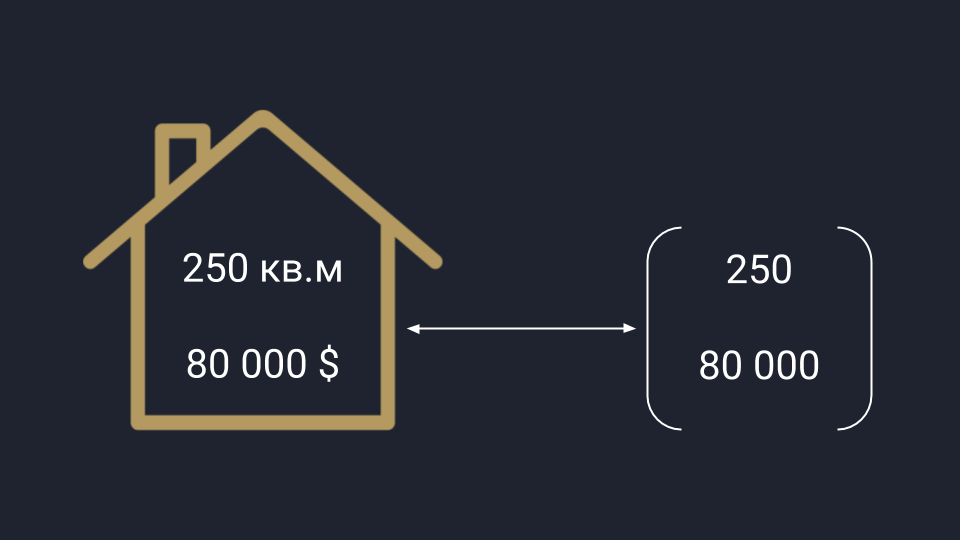Аналитическое представление вектора: данные можно перевести в числа

Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

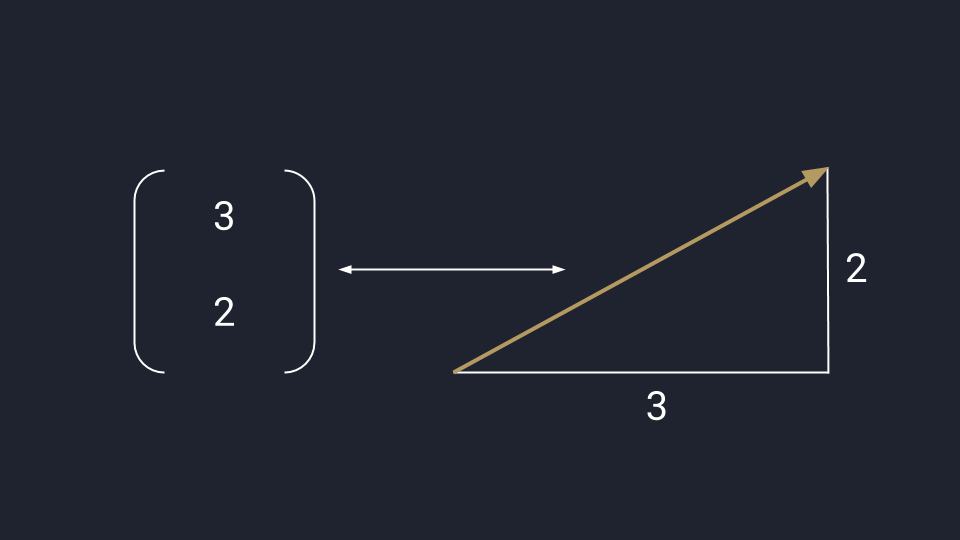Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

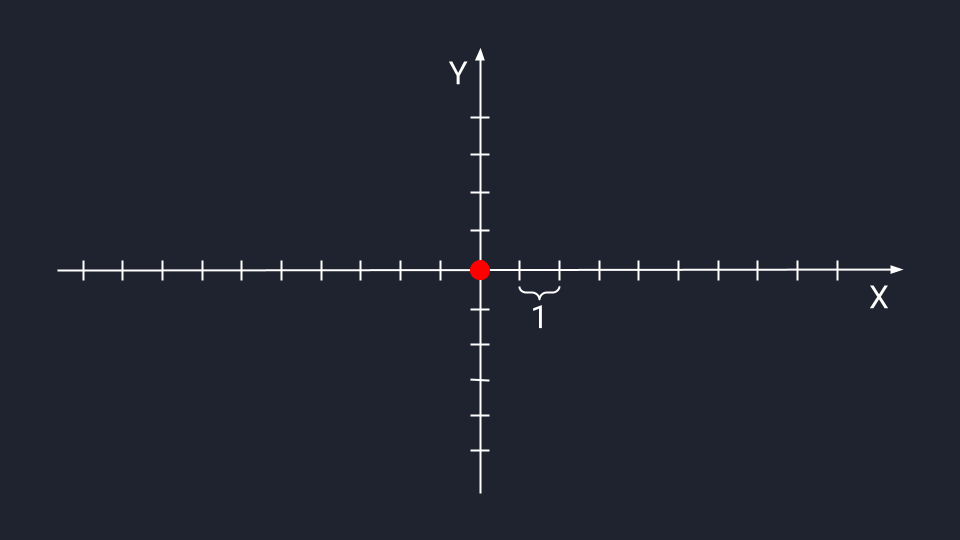Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор

конца

Суммой векторов

Кстати, если вектор

начала
правило параллелограмма

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности:

Произведением ненулевого вектора

Правило умножения вектора на число легче понять с помощью рисунка:

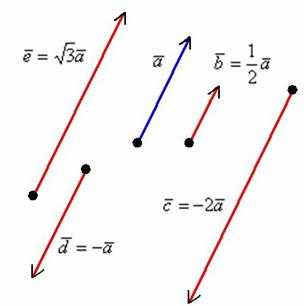
Разбираемся более детально:

1) Направление. Если множитель

меняет направление

2) Длина. Если множитель заключен в пределах

уменьшается
увеличивается

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,

Обратное тоже справедливоесли мы умножаем вектор на число, то получится коллинеарныйвектор

4) Векторы

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Какие сведения нельзя хранить в Единой биометрической системе

В информационных системах организаций, осуществляющих аутентификацию
на основе биометрических персональных данных физических лиц, запрещена
обработка, включая сбор и хранение, используемых в целях идентификации и
аутентификации биометрических персональных данных, за исключением случаев,
связанных с размещением данных в ЕБС и подтверждением соответствия
предоставленных биометрических персональных данных физического лица
соответствующим векторам из ЕБС. Также допускается хранение биометрических
персональных данных для целей рассмотрения обращений субъектов персональных
данных, предполагающих неправомерную обработку их биометрических персональных
данных при проведении аутентификации и оспаривающих результаты проведения
аутентификации, в течение не более десяти суток с момента предоставления таких
данных.

В ЕБС, ее региональных сегментах и информационных системах
организаций, аккредитованных на проведение биометрической идентификации,
запрещается обработка, сбор и хранение геномной информации и сведений,
отнесенных к государственной тайне. Также запрещается обработка сведений,
позволяющих отнести физических лиц к отдельным категориям, участие которых в
правоотношениях регулируется законами «Об учреждениях и органах
уголовно-исполнительной системы РФ», «О содержании под стражей подозреваемых и
обвиняемых в совершении преступлений», «О ФСБ», «О государственной защите
судей, должностных лиц правоохранительных и контролирующих органов», «Об оперативно-розыскных
мероприятиях», «О государственных охране», «О государственной защите
потерпевших, свидетелей и иных участников уголовного судопроизводства», «О
полиции» и «О войсках национальной гвардии».

Безопасные коммуникации сотрудников: что важно знать
бизнес-коммуникации

ФСБ (Федеральная служба безопасности), Росгвардия, органы
обеспечения государственной защиты (в частности, Министерство внутренних дел),
Федеральная служба охраны (ФСО) и Служба внешней разведки (СВР) вправе
направлять мотивированный запрос оператору ЕБС и операторам ее региональных
сегментов о блокировании, удалении, уничтожении биометрических
персональных данных отдельных физических лиц, о внесении изменений в сведения,
содержащиеся в ЕБС и ее региональных сегментах, а также обрабатывать сведения в
случае и в порядке, установленных законом.

Банки, многофункциональные центры предоставления
государственных и муниципальных услуг и иные организации в случаях, определенных
федеральными законами, после проведения идентификации при личном присутствии
физического лица с его согласия на безвозмездной основе размещают в электронной
форме.

Физические лица вправе размещать с использованием мобильного
приложения ЕБС свои биометрические персональные данные в ЕБС с применением
пользовательского оборудования, имеющего в своем составе идентификационный
модуль. Также физические лица вправе размещать с использованием российской
программы для ЭВМ, предназначенной для обработки биометрических персональных
данных, функционирующей с применением шифровальных средств и предоставляемой на
безвозмездной основе оператором ЕБС или ее регионального сегмента, свои
биометрические персональные данные в региональном сегменте ЕБС с применением
пользовательского оборудования.

Государственные органы не позднее чем за 30 дней до
планируемого размещения биометрических персональных данных в ЕБС обязаны
уведомить субъекта персональных данных в любой позволяющей подтвердить факт
получения уведомления форме о таком размещении. В случае получения до истечения
указанного срока возражения от субъекта персональных данных против размещения
его персональных данных в ЕБС такое размещение не осуществляется. Субъект
персональных данных вправе обратиться к оператору ЕБС с требованием о
блокировании или об уничтожении персональных данных.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Дезинформация

Дезинформацией (также дезинформированием) называется один из способов манипулирования информацией, как то введение кого-либо в заблуждение путём предоставления неполной информации или полной, но уже не нужной информации, или полной, но не в нужной области, искажения контекста, искажения части информации.

Цель такого воздействия всегда одна — оппонент должен поступить так, как это необходимо манипулятору. Поступок объекта, против которого направлена дезинформация, может заключаться в принятии нужного манипулятору решения или в отказе от принятия невыгодного для манипулятора решения. Но в любом случае конечная цель — это действие, которое будет предпринято.

Понятие вектора

Происхождение и цель

Концепция векторов была первоначально разработана в середине 19 века для описания сил в трехмерном пространстве. С тех пор они широко использовались в различных областях исследований. В математике и физике они обеспечивают способ количественной оценки физических величин, которые имеют как величину, так и направление, таких как перемещение, скорость и ускорение. В информатике они используются для хранения данных в базах данных, алгоритмах машинного обучения и графических представлениях и манипулирования ими. По сути, векторы позволяют нам понимать и представлять окружающий мир математическим или символическим способом.

Фундаментальные элементы вектора

Направление: Направление вектора — это то, на что он указывает. Это может быть представлено геометрически углом, который вектор образует с осью отсчета, или алгебраически знаками и значениями его компонентов в каждом измерении

Важно помнить, что векторы, имеющие одно и то же направление, могут иметь разную величину

Величина: Величина вектора по существу является его длиной или размером и всегда является неотрицательным вещественным числом. Он представляет собой «количество» величины, описываемой вектором. Например, если вектор представляет собой силу, то его величина будет равна силе этой силы.

Иллюстрации и примеры

Векторы могут быть визуализированы множеством способов в зависимости от их размерности:

В двух измерениях вектор можно представить как стрелку, нарисованную на плоском листе бумаги, с концом в начале координат (0,0) и кончиком в определенной точке (x,y).

В трех измерениях вектор можно рассматривать как стрелку в пространстве, простирающуюся от начала координат (0,0,0) до определенной точки (x,y,z).

В более чем трех измерениях визуализация становится менее интуитивной, но принципы остаются прежними. Каждое измерение добавляет к вектору еще один компонент, и он все еще может быть описан его величиной и направлением, даже если мы не можем легко его визуализировать.

Примером вектора может быть автомобиль, движущийся на северо-восток со скоростью 60 миль в час. Величина вектора равна 60 (скорость), а направление — северо-восток. Сила в 10 Н, действующая вниз, также представляет собой вектор, величина которого равна 10 Н, а направление — вниз.

Классификация информации

Информацию можно разделить на виды по различным критериям:

по способу восприятия:

• Визуальная — воспринимаемая органами .
• Аудиальная — воспринимаемая органами .
• Тактильная — воспринимаемая рецепторами.
• Обонятельная — воспринимаемая рецепторами.
• Вкусовая — воспринимаемая рецепторами.

по форме представления:

•  — передаваемая в виде символов, предназначенных обозначать лексемы языка.
•  — в виде цифр и знаков, обозначающих математические действия.
•  — в виде изображений, предметов, графиков.
•  — устная или в виде записи и передачи лексем языка аудиальным путём.

по назначению:

•  — содержит тривиальные сведения и оперирует набором понятий, понятным большей части .
• Специальная — содержит специфический набор понятий, при использовании происходит передача сведений, которые могут быть не понятны основной массе социума, но необходимы и понятны в рамках узкой социальной группы, где используется данная информация.
• Секретная — передаваемая узкому кругу лиц и по закрытым (защищённым) каналам.
• (приватная) — набор сведений о какой-либо личности, определяющий социальное положение и типы социальных взаимодействий внутри популяции.

по значению:

• Актуальная — информация, ценная в данный момент времени.
• Достоверная — информация, полученная без искажений.
• Понятная — информация, выраженная на языке, понятном тому, кому она предназначена.
• Полная — информация, достаточная для принятия правильного решения или понимания.
• Полезная — полезность информации определяется субъектом, получившим информацию в зависимости от объёма возможностей её использования.

по истинности:

Сложение и вычитание векторов

      Для того, чтобы найти сумму двух произвольных векторов     и     нужно совместить начало вектора     с концом вектора   .   Тогда началом вектора     будет начало вектора   ,   а концом вектора     будет конец вектора     (рис.9).

Рис.9

      При этом, если

      и      

то

      Этот факт часто формулируют так: «При сложении векторов их координаты складываются».

      Для того, чтобы найти разность двух произвольных векторов     и     нужно воспользоваться формулой

      Операция вычитания двух векторов наглядно изображена на рисунке 10.

Рис.10

      При этом, если

      и      

то

      Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора   ,   нужно из координат вектора     вычесть координаты вектора   ».

Энциклопедия Брокгауза и Ефрона

— те физические количества, которым приписывают не только величины, но и направления, называют векториальными величинами; таковы, например, силы, скорости, ускорения, количества движений, моменты сил и количеств движений вокруг точек и проч. Эти количества изображают длинами, заключающими в себе столько единиц длины и частей ее, сколько в рассматриваемой векториальной величине заключается единиц величины и частей ее; длину эту проводят в направлении, свойственном изображаемой векториальной величине. В механике и математической физике почти в каждом вопросе приходится рассматривать векториальные количества и производить над ними различные действия аналитического и геометрического характера, причем оказывается, что векториальные количества различных наименований обладают многими аналогичными свойствами. Так, например, при известных условиях, силы, количества движения, скорости, ускорения, угловые скорости и моменты слагаются по правилу параллелограмма. Далее, теория моментов системы сил, приложенных к твердому телу, оказывается аналогичною теории скоростей точек твердого тела. По этой причине признано полезным и возможным составить общую теорию векторов, подразумевая под вектором длину, проведенную из какой-либо точки в каком-либо направлении. Каждый вектор определяется тремя величинами: длиною и двумя углами, определяющими направление вектора, или же тремя проекциями вектора на оси координат. Теорию векторов, то есть изложение различных действий над векторами, можно теперь найти в различных новейших курсах механики. В самом стройном виде теория векторов является в учении о кватернионах, основанном У. Гамильтоном (см. Кватернионы).

Главным вектором совокупности сил, приложенных к системе материальных точек или к разным точкам твердого тела, называется геометрическая сумма всех этих сил (см. Геометрическая сумма), или, иначе говоря, равнодействующая, которую имели бы все эти силы, если бы они были приложены к одной и той же точке.

Радиусом-вектором какой-либо точки относительно какого-либо центра называется длина, проведенная из центра к точке.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора  и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор  от конца вектора :

Суммой векторов  и  является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов  представляет собой вектор результирующего перемещения  с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор  отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация:  (векторы сонаправлены) или  (векторы направлены противоположно).

Произведением ненулевого вектора  на число  является такой вектор , длина которого равна , причём векторы   и  сонаправлены при  и противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка:

Разбираемся более детально:

1) Направление. Если множитель  отрицательный,  то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах  или , то длина вектора уменьшается. Так, длина вектора  в два раза меньше длины вектора . Если множитель  по модулю больше единицы, то длина вектора увеличивается в  раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно  коллинеарны

Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы  сонаправлены. Векторы  и  также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Операции над отрезками

Любые геометрические свойства векторов можно перенести на систему координат — как двоичную, так и троичную. Впоследствии приобретаются алгебраические характеристики, что упрощает способы вычисления. Можно привести в пример несколько классических операций:

• Модуль. Это то же самое, что и длина.
• Сложение. Высчитывается путем суммирования координатных слагаемых.
• Модуль суммы. Вычисляется посредством теоремы косинусов.
• Вычитание. Высчитывается путем получения разности соответствующих координатных показателей.
• Модуль разности. Здесь также задействуется теорема косинусов, однако перед угловой величиной ставится знак минус.
• Умножение на число. Если показатель имеет положительное значение, то вектор будет сонаправленным, больше в указанное количество раз. Если отрицательное, то противоположно ориентированным.
• Скалярное произведение. Вычисляется через геометрические характеристики. В формуле присутствует значение косинуса — рассматривается угол, который образуется, если отрезки наложить друг на друга, но направление оставить прежним.
• Векторное произведение. Для вычисления задействуется трехмерное пространство. Чтобы получить результат, необходимо чертить перпендикулярно расположенный вектор (относительно двух других).

Сложнее всего выполняются операции по произведению. Здесь задействуются алгебраические и геометрические свойства. Удобнее видеть чертеж, ориентироваться по нему. Когда отрезки наложены друг на друга либо имеется перпендикуляр (в трехмерном пространстве), выводить математические значения намного проще.