Умножение вектора на число

Возможно ли умножение вектора на число

Определение

Вектор является направленным отрезком прямой, то есть представляет собой отрезок с обозначенными граничными точками, одна из которых определяет его начало, в вторая — конец.

Произведением вектора \(\bar{a}\), не равного нулю, на число \(\lambda \ne 0\) является вектор \(\lambda \bar{a},\) коллинеарный заданному, то есть он будет сонаправлен данному вектору \(\bar{a}\), если \(\lambda>0\), и противоположно направленным — если \(\lambda<0\), а его модуль равен модулю данного вектора, умноженному на модуль числа:

\(\lambda >0:\lambda \bar{a}\uparrow \uparrow \bar{a}\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

\(\lambda <0:\lambda \bar{a}\uparrow \downarrow \bar{a}\)

\(\left|\lambda \bar{a}\right|=\left|\lambda \right|\cdot \left|\bar{a}\right|\)

В том случае, когда вектор \(\bar{a}\ne \bar{0}\) задают с помощью координат, то произведение этого вектора на число \(\lambda \ne 0\) является вектором \(\lambda \bar{a}\) с координатами, равными соответствующим координатам заданного вектора \(\bar{a}\), умноженным на число \(\lambda:\)

\(\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\Rightarrow \lambda \bar{a}=\left(\lambda a_{1} ;\; \lambda a_{2} ;\; \lambda a_{3} \right)\)

Особенность такого действия, как умножение вектора на число заключается в том, что число является простой численной формой величины, для которого отсутствует направление, а вектор определяется в качестве направленного отрезка, обладающего численным измерением и направлением.

Подобная операция, как и вычитание, нередко используется при решении задач в математике, геометрии и физике.

Пример

В качестве примера можно рассмотреть случай из теории, при котором по дороге движутся машины в количестве двух штук. При этом скорость первого автомобиля составляет 30 км/ч, а второго — 60 км/ч. Достаточно просто определить, что вторая машина передвигается со скоростью, которая в два раза больше, чем скорость первой машины. Таким образом, скорость второго транспортного средства допустимо выразить с помощью скорости первого автомобиля путем умножения скорости первой машины на два.

Произведение ненулевого вектора \(\vec{a}\) на число k является таким вектором \(\vec{b}\), длина которого составляет \(\left| \vec{b}\right|=\left|k \right|*\left|\vec{a} \right|\). При этом векторы \(\vec{a}\) и \(\vec{b}\) сонаправлены, если k больше или равно нулю, и противоположно направлены, когда k меньше нуля. Произведение нулевого вектора на любое число в результате позволяет получить ненулевой вектор.

Предположим, что существует некий вектор \(\vec{a}\). В таком случае вектор \(\vec{2a}\) является вектором, направленным в ту же сторону, но с длиной, которая в 2 раза превышает длину вектора \(\vec{a}\). Длина его в два раза больше. Вектор \(\vec{-2a}\) является вектором, который направлен противоположно вектору \(\vec{a}\) и длиннее его в 2 раза.

Сложение и скалярное умножение векторов — Концепция

Сложение и скалярное умножение векторов являются основными операциями, которые можно выполнять, используя их геометрическое или алгебраическое представление.

умножение векторов

компонентов вектора
горизонтальная составляющая
вертикальная составляющая
форма компонента
сложение векторов
нулевой вектор
скалярное умножение

Теперь, когда у нас есть понятие компонентов векторов, мы можем переопределить способ сложения векторов, а также ввести другую операцию, называемую скалярным умножением. Добавляя векторы алгебраически, предположим, что у нас есть два вектора, данные нам в компонентной форме, поэтому u — это u1, запятая u2, а вектор v — это v1, запятая v2.

Сложение и вычитание векторов. Умножение вектора на число в координатах 9 класс онлайн-подготовка на Ростелеком Лицей |

Напоминание предыдущего материала

Ранее для выполнения действий с векторами мы применяли правило треугольника, правило параллелограмма, сжимали или растягивали вектор. Теперь мы научимся выполнять действия над векторами в координатах.

Пример

Даны векторы , ,  (см. рис. 1).

Рис. 1. Задача о сложении векторов

Найти:

Решение

Из произвольной точки  строим вектор . Далее из конца вектора  строим вектор , он сонаправлен вектору , а длина в два раза больше. Теперь из конца вектора  строим вектор , он противоположно направлен вектору , а длина в 4 раза больше. Теперь соединяем точку  и конец вектора  – получен ответ, вектор  (см. рис. 2).

Рис. 2. Решение задачи

Пусть заданы два неколлинеарных вектора. Будучи отложены из одной точки, они задают косоугольную систему координат (см.

Рис. 3. Косоугольная система координат

Любой третий вектор однозначно выражается через векторы , :

Пара чисел  однозначно задает вектор – это и есть его координаты: .

Сложение векторов в координатах

Теорема

Дано:; .

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

Тогда сумма:

Что и требовалось доказать: .

Умножение вектора на число в координатах

Теорема

Дано:.

Доказать:.

Доказательство

В системе координат относительно векторов ,  имеем:

Умножим обе части равенства на число :

Что и требовалось доказать: .

Вычитание векторов в координатах

Рассмотрим разность векторов.

Дано: ; .

Координаты вектора  определяем как координаты вектора, умноженного на число:

Тогда разность векторов:

Решение примеров

Пример

Доказать, что если два вектора коллинеарны, то их координаты пропорциональны.

Решение

Дано: ; , .

Доказать: ; .

По определению коллинеарных векторов векторы  и  лежат на одной прямой или на параллельных прямых. В таком случае вектор  можно получить из вектора  умножением на некоторое число:

 по условию;  по правилу умножения вектора на число.

Равные векторы имеют равные координаты, отсюда:

Что и требовалось доказать.

Пример

; ; ;

Найти попарно коллинеарные векторы.

Решение

Очевидно, что нужно искать пропорциональные координаты. Рассмотрим первый и третий векторы:

Получено верное равенство, следовательно, векторы коллинеарны: .

Рассмотрим второй и четвертый векторы:

Также получено истинное выражение, а значит, векторы коллинеарны: .

Ответ:; .

Вывод

Итак, мы научились складывать и вычитать векторы, умножать вектор на число в координатах.

Список литературы

1. Атанасян Л.С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.

2. Фарков А.В. Тесты по геометрии: 9 класс. К учебнику Л.С. Атанасяна и др. – М.: Экзамен, 2010.

3. Погорелов А.В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт mathprofi.ru (Источник)

2. Интернет-сайт cleverstudents.ru (Источник)

3. Интернет-сайт edu.dvgups.ru (Источник)

Домашнее задание

1. Вектор  с началом в точке  имеет координаты .

2. Заданы векторы  и . Найти координаты вектора .

3. Даны векторы  и . Найти векторы ; .

4.Даны векторы ,  и . Найти   и  

Откладывание вектора от данной точки

Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Определение 1

Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

1. Вектор $overrightarrow{a}$ — нулевой.

   В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.

2. Вектор $overrightarrow{a}$ — ненулевой.

   Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ — конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

   Рисунок 2. Иллюстрация теоремы 1

   Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

   Теорема доказана.

оборотов

Next:

Up: Previous: Содержимое

Для наших пассивных вращений мы перейдем от одного ортонормированного правого базиса к другому ортонормированному,

Если мы вращаем оси координат, мы можем вычислить вектор в новых (штрихованных) координатах
исходного вектора путем умножения на Матрица вращения .

Немного подумав, мы можем вычислить элементы матрицы поворота .
Давайте вычислим вектор
, вектор положения в повернутых координатах.
Чтобы получить
компонент
, просто возьмите вектор и добавьте точки к новому единичному вектору , записанный в исходных координатах.

Таким образом, матрица вращения просто дается

Таким образом, каждый элемент матрицы поворота представляет собой просто косинус угла между новой осью координат и старой осью координат.

Физически легко увидеть, что произведение двух вращений есть просто какое-то другое вращение.

группа

В качестве примера сделаем поворот на небольшой угол
в
самолет, покидая
ось без изменений.
Угол между
и
ось
.
Угол между
и
ось тоже
.
Угол между
и
ось .
Угол между
и
ось .

Итак, мы можем написать матрицу вращения.

В трех измерениях вращение в
можно сказать, что самолет вращение вокруг
ось .
Это не так в четырех измерениях.

Можно запишите скалярное произведение между двумя векторами только с точки зрения длин векторов.

Воспользуемся тем, что
Скалярные произведения являются инвариантными для получения свойства матриц вращения.

, обратная матрице вращения, является ее транспонированием Ортогональные матрицы Специальная ортогональная группа SO(3) Ортогональная группа O(3)

Как найти векторное произведение двух векторов: формула, свойства, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Векторное произведение векторов

В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.

• Геометрическая интерпретация
• Формула векторного произведения
• Свойства векторного произведения
• Пример задачи

Геометрическая интерпретация

Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как или a x b.

Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.

При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).

Свойства векторного произведения

1.

= 0, если

2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.

S_парал. = |a x b|

3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.

S_Δ = 1/₂ · |a x b|

4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.

c ⟂ a, c ⟂ b.

5. a x b = –b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.

Решение:

Ответ: a x b = {19; 43; -42}.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Понятие, основные свойства

В том случае, когда вектор \(\vec{b}\) равен произведению ненулевого числа k и ненулевого вектора \(\vec{a}\), то есть \(\vec{b}=k*\vec{a}\), справедливы следующие утверждения:

• \(\vec{a}\parallel\vec{b}\), то есть рассматриваемые вектора параллельны;
• \(\vec{a}\) и \(\vec{b}\) обладают одинаковым направлением при k больше нуля;
• \(\vec{a}\) и \(\vec{b}\) обладают разными направлениями при k меньше нуля.

Вектор можно умножить на число в виде скалярной величины. При этом в результате получится тоже вектор. После операции умножения длина заданного вектора изменится:

• длина вектора будет увеличена при умножении на число, модуль которого больше 1;
• длина вектора уменьшится в том случае, когда модуль числа меньше 1.

Если вектор умножить на положительное число, полученный вектор будет обладать таким же направлением, что и первоначальный. В том случае, когда предполагается произведение вектора на отрицательное число, полученный в результате вектор будет направлен в противоположную сторону.

 
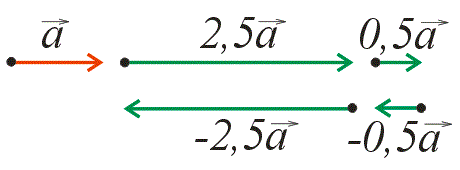
Примечание

При произведении вектора на число, он не может быть повернут на какой-либо угол по отношению к исходному положению. Таким образом, заданный и полученный векторы параллельны друг другу.

В том случае, когда есть информация о координатах вектора, при умножении его на число следует умножить каждую координату рассматриваемого вектора на данное число.

\(\vec{a}=\left\{a_{x};a_{y} \right\}\)

Данная запись представляет собой координаты вектора \(\vec{a}.\)

\(k*\vec{a}=\left\{k*a_{x};k*a_{y} \right\}\)