Таблица квадратов натуральных чисел от 1 до 99

Что такое таблица квадратов натуральных чисел

Определение

Квадрат чисела — это число, возведенное во вторую степень, то есть умноженное само на себя.

(a^2=acdot a)

Эта операция называется так, потому что аналогична вычислению площади квадрата.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Определение

Таблица квадратов — это таблица, в которой содержатся квадраты чисел.

С помощью таблицы в алгебре решают квадратные уравнения: возводят числа в квадрат и вычисляют квадратный корень. В геометрии ей пользуются при решении задач с теоремой Пифагора или теоремой косинусов.

Как правило, в таблице по вертикали указаны десятки, а по горизонтали — единицы. На пересечении находится квадрат искомого числа.

Глава 2. Способ с применением таблицы квадратов

Двузначных чисел

С этим способом мы познакомились на уроках математики. Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора. Но для этого метода требуется наличие таблицы квадратов натуральных чисел от 10 до 99. (Она есть во всех учебниках алгебры 8 класса, и на экзамене ГИА предлагается в качестве справочного материала).

Откройте таблицу и проверьте скорость нахождения ответа. Но при использовании таблицы квадратов для извлечения квадратного корня нужно не перепутать, что крайний левый столбик определяет цифру, стоящую в разряде целых, а самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее 100 подкоренное число, и далее действуйте по правилам этой таблицы.

Пример 1: Найдём значение

.

Решение: Мысленно отбрасываем две последние цифры у всех чисел в таблице и находим 57 или близкие к 57-ти – такое число одно 5776. Левый столбик даёт ответ 7 (это целые), а верхняя строчка 6 (это десятые). Значит

Пример 2: Найдём значение

.

Решение: Мысленно поставим запятые, отсчитав две последние цифры, у всех чисел в таблице и находим близкие для 89 – таких только два 88,36 и 90,25. Но 90,25 – это много, 88,36 ближе к 89. Значит, выбираем 8836.

Левый столбик даёт ответ 9 (это целые), а верхняя строчка 4 (это десятые). Значит

Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 мы уже этим способом извлечь не сможем. Способ удобен для заданий с маленькими корнями и при наличии таблицы.

Глава 3. Формула Древнего Вавилона

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа n.

Число n они представляли в виде суммы а 2 + b, где а 2 ближайший к числу n точный квадрат натурального числа а и пользовались формулой:

Извлечём с помощью этой древней формулы корень квадратный из числа 40:

Результат извлечения корня из 40 с помощью микрокалькулятора равен 6,324555. Как видим, способ вавилонян дает хорошее приближение к точному значению корня. Но без знания полных квадратов больших чисел и умения их быстро находить, результат извлечения будет найти крайне затруднительно.

Глава 4. Через решение уравнения

На самом деле существует удобный способ нахождения квадратного корня «вручную» через решение уравнения, ведь математика — наука с многовековой историей, а калькуляторы были не всегда. Способ этот дает возможность вычислить значение корня с точностью до одного — двух знаков после запятой, а, при желании, достичь и большей точности. Звучит невероятно, но попробуйте испытать этот способ при вычислении квадратного корня.

Суть этого способа рассмотрим на примере и попробуем вычислить значение

Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 16 = 4² и 25 = 5²,

поэтому

следовательно

х

Возведем в квадрат обе части полученного уравнения и раскроем скобки при помощи формулы суммы квадрата:

(

х)ххх

Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х²явно достаточно малая дробь, то ей вполне можно пренебречь.

В результате приходим к простому линейному уравнению

Решив его, получаем значение х = 0,5.

Значит

На самом деле, при расчете на калькуляторе, значение этого корня равно 4,47213595, то есть погрешность при нашем расчете составила 0,02786405. Не правда ли, вполне приличная точность!

Но если все же решение задач по математикетребует еще большей точности, то можно достичь ее тем же способом, просто продолжив вычисления с уже полученным значением корня. Так что подобный способ вычисления квадратного корня необычайно точен и удобен, а погрешность вычисления зависит исключительно от вашего терпения и упорства.

Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.

Дата добавления: 2019-01-14 ; просмотров: 301 ; Мы поможем в написании вашей работы!

Источник

Дизайнерские решения в небольшой квартире-студии

Сегодня наметилась тенденция роста тарифов за коммунальные услуги, и многие семьи предпочитают арендовать или приобретать компактное жилье. Используя готовые примеры на фото, проще сориентироваться в последних модных тенденциях, среди которых актуальны квартиры студийного типа. Предлагается выбрать понравившийся дизайн-проект квартиры 35 кв.м или разработать свою версию на основе понравившихся фото.

Популярны готовые наработки дизайна квартиры-студии 35 кв.м, но нередко это разумное преобразование тесной однокомнатной квартиры. Конечно, у них есть свои преимущества и недостатки, как и у любого решения.

Основное достоинство «студийки» – достаточно свободной площади в проходах. Это отличный вариант для супружеской пары, но в домах без стен не обойтись без условного разграничения общего пространства. Согласитесь, попадая с порога в интерьер квартиры 35 кв. м. без внутренних стен, неприятно сразу очутиться в спальне или туалете. Поэтому тут нужен некоторый дизайнерский опыт.

В качестве разделителя зон подойдет ширма, красивый витраж или оригинальная перегородка

Зонирование – это разделение на функциональные или целевые участки, но разграничение может быть и достаточно условным. Когда нужно реально отгородить личное пространство, используют перегородки разного типа. Иногда первостепенными остаются дизайнерские акценты, но им отведена разделительная роль. В предпочтении функциональное зонирование с прозрачными стеклянными или вуалевыми перегородками.

Готовые модели мебели не всегда удобны и занимают много места, лучше найти практичные решения и сделать мебель по своим чертежам

При выборе мебели для квартиры-студии рекомендуется определить размеры обустраиваемого пространства

Притом важно их знать не только с разметкой пола, но и по вертикали. Намного удобнее, когда кухонный гарнитур занимает всю стену до потолка, чтобы по максимуму спрятать за дверцы:

• посуду;
• технику;
• пищевые припасы;
• кухонную утварь.

Для квартиры студийного типа актуальными остаются барные стойки, выполняющие функцию зонирования между кухней и гостиной или столовой. Технику приобретайте с минимальным порогом шума, используя в такое время, чтобы не мешать другим.

Лоджию или балкон можно утеплить и организовать рабочий кабинет

Если говорить об экономии пространства, то не стоит отказывать себе в большом многоместном диване, трансформирующимся в просторную двуспальную кровать. Это даст возможность объединить гостиную и спальню.

Остается выделить место для удобных кресел у телевизионной панели, столового гарнитура с обеденным столом и компьютерного (рабочего) уголка с полками под бумаги.

У каждой функциональной зоны должно быть свое локальное освещение.

При грамотном подходе к организации освещения можно создать иллюзию простора

Душевой бокс и туалет обязательно изолируют сплошными непроницаемыми перегородками.

Прихожая может плавно перетекать в гостевую зону без разграничений, но визуально зоны должны отличаться отделочными материалами и меблировкой.

Прихожая станет визуально шире с белыми стенами

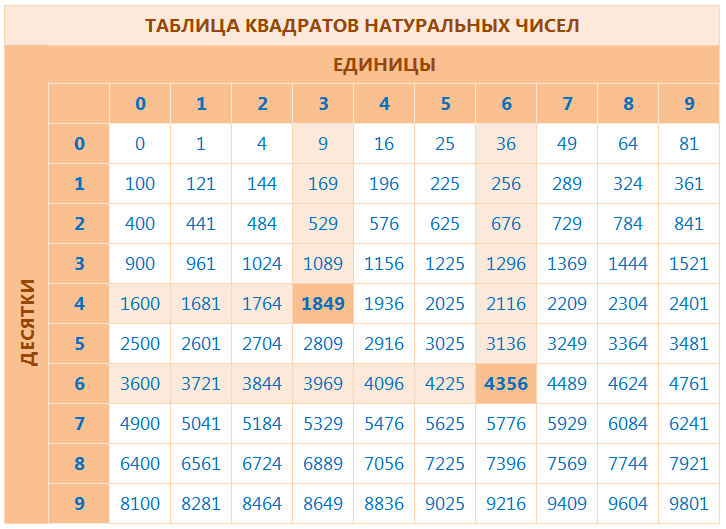
Как пользоваться таблицей квадратов по схеме:

Чтобы возвести число в квадрат, нужно выбрать десятку и единицу числа, которое необходимо возвести во вторую степень, и на их пересечении будет число, которое получается за счет умножения этого числа на себя.

Например: рассмотрим на картинке ниже число 1849. Оно получилось за счет умножения числа 43 на 43 (43 во второй степени), в котором “4”- это десятка, а “3” – единица.

Или другой пример: число 4356 получилось за счет умножения числа 66 на 66 (66 во второй степени), в котором “6” сбоку – это десятка, а “6” сверху – единица.

Таблица квадратов:

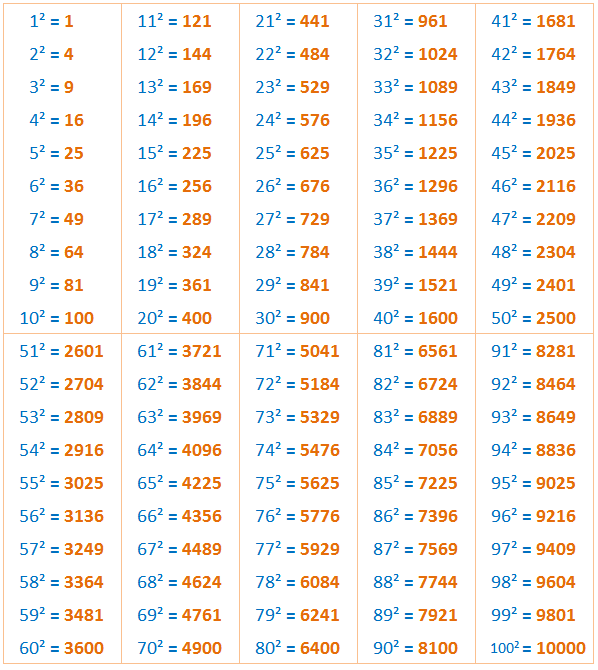
Вторую степень называют “квадратом числа”. При этом умножение числа самого на себя происходит один раз (a · a).

Квадратное число в геометрическом представлении может выглядеть, как квадрат. Например, число 9 – можно представить в виде квадрата из 9 точек, где стороны квадрата будут составлять по 3 точки.

Метод Герона

Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:

где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.

Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:

√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.

Теперь проверим точность метода:

Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:

√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.

Проверим точность расчёта:

После повторного применения формулы погрешность стала совсем незначительной.

Таблица квадратов натуральных чисел от 1 до 99

единицыдесятки	1	2	3	4	5	6	7	8	9
1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Таблица квадратов до 1012 = 122 = 432 = 942 = 1652 = 2562 = 3672 = 4982 = 6492 = 81102 = 100	Таблица квадратов до 20112 = 121122 = 144132 = 169142 = 196152 = 225162 = 256172 = 289182 = 324192 = 361202 = 400	Таблица квадратов до 30212 = 441222 = 484232 = 529242 = 576252 = 625262 = 676272 = 729282 = 784292 = 841302 = 900	Таблица квадратов до 40312 = 961322 = 1024332 = 1089342 = 1156352 = 1225362 = 1296372 = 1369382 = 1444392 = 1521402 = 1600	Таблица квадратов до 50412 = 1681422 = 1764432 = 1849442 = 1936452 = 2025462 = 2116472 = 2209482 = 2304492 = 2401502 = 2500
Таблица квадратов до 60512 = 2601522 = 2704532 = 2809542 = 2916552 = 3025562 = 3136572 = 3249582 = 3364592 = 3481602 = 3600	Таблица квадратов до 70612 = 3721622 = 3844632 = 3969642 = 4096652 = 4225662 = 4356672 = 4489682 = 4624692 = 4761702 = 4900	Таблица квадратов до 80712 = 5041722 = 5184732 = 5329742 = 5476752 = 5625762 = 5776772 = 5929782 = 6084792 = 6241802 = 6400	Таблица квадратов до 90812 = 6561822 = 6724832 = 6889842 = 7056852 = 7225862 = 7396872 = 7569882 = 7744892 = 7921902 = 8100	Таблица квадратов до 100912 = 8281922 = 8464932 = 8649942 = 8836952 = 9025962 = 9216972 = 9409982 = 9604992 = 98011002 = 10000

Интерьер функциональных зон

Для обеспечения максимального комфорта, следует создать продуманный и стильный дизайн каждого уголка в квартире.

Кухня

В малогабаритной кухне не следует устанавливать громоздкие гарнитуры темного цвета. Для экономии полезной площади лучше отказаться от обеденного стола грубой прямоугольной или квадратной формы. Его можно заменить компактной овальной моделью с округлыми стульями, барной стойкой или переоборудовать под него подоконник.

Визуально увеличить комнату поможет светлая отделка потолка и стен. Для напольного покрытия подойдут древесные оттенки. Такой монотонный дизайн отлично дополнят яркие акценты, например, в виде кухонного фартука в ярком исполнении. Окно выгодно украсят легкие полупрозрачные занавеси. 

На фото дизайн совмещенной кухни-гостиной в интерьере евродвушки 36 кв. м.

Гостиная и зона отдыха

В гостиной, имеющей средние габариты, уместно применение универсальных белых, бежевых или серых оттенков в комбинации с другими тонами. В качестве напольного покрытия используют ламинатную доску или паркет, придающий интерьеру домашнего уюта. Стены облицовывают обоями или другим однотонным покрытием со слабовыраженным рисунком.

Для обустройства зала выбирают только самую необходимую меблировку, в виде дивана, журнального столика и различных систем хранения. Рациональное решение представляют собой угловые конструкции, эффективно использующие неактивное пространство и сохраняющие место для перемещения в комнате.

На фото зона отдыха с компактным диванчиком и журнальным столиком в светлых тонах, в квартире двушке 36 кв. м.

Детская

Для более эргономичного дизайна детскую оборудуют с помощью кровати-чердака с письменным столом на нижнем ярусе. Семье с двумя детьми подойдет установка двухъярусной конструкции. Сохранить полезные квадратные метры помогут кровати, оснащенные выдвижными ящиками и купейный шкаф, вмонтированный в нишу.

В однокомнатной квартире, уголок ребенка, лучше отделить облегченными перегородками или декоративными занавесками, для создания качественного вентилирования пространства. Данный участок следует оборудовать правильным освещением, в виде настенных бра и настольных светильников для рабочего места, подсветки или неяркого ночника для спальной зоны.

На фото дизайн малогабаритной детской для девочки в двушке 36 квадратов.

Спальня

В дизайне маленькой спальни будет особенна уместна встроенная мебель. Довольно интересной идеей для размещения вещей станут открытые стойки или вешалки под потолком. При наличии выдвижного или подъемного механизма кровати, систему хранения оборудуют внутри нее. В изголовье иногда размещают полки и ящики.

Отличным решением для отдельно выделенной спальной зоны в однушке или студии, станет подиум или ниша, в которую можно полностью или частично установить кровать. Для отделения пространства, углубление оформляют занавесками или раздвижными перегородками.

Рабочее место

Практичным и эргономичным решением для рабочего места, является его расположение в качестве продолжения подоконника или обустройство на балконе. Такой вариант не только способствует экономии площади и отличается стильным видом, но и предоставляет комфортные условия для работы. В вечернее время, данный участок должен иметь качественное освещение, в этом помогут точечные светильники и настольная лампа.

Ванная и туалет

В совмещенном санузле, для освобождения дополнительной площади, ванну с легкостью заменит душевая кабинка. Таким образом получится разместить в комнате стиральную машину или другие нужные предметы. Для максимальной экономии пространства, лучше использовать высокие узкие шкафы, полочки, в отделке применять светлую цветовую гамму, стеклянные и зеркальные поверхности.

На фото интерьер совмещенного санузла, выполненный бело-бежевых тонах в дизайне квартиры 36 кв.

Сколько будет 27 при мощности -2 / 3?

Определение.

Квадрат а является произведением двух факторов, каждый из которых совпадает с а.

Квадрат a обозначает a2. Читайте: «a в поле».

Используя формулу, определение квадрата а можно записать в виде:

Слагаемые a2 называются квадратом числа a, так как эта формула выражает квадрат квадрата со стороной a.

Чтобы найти квадрат определенного числа, это число должно быть взято в два раза, а произведение рассчитано.

К примеру,

Если числовое выражение содержит квадрат числа, квадратное значение вычисляется до остальных действий.

К примеру,

В математике поиск квадратов чисел достаточно часто.

Для ускорения расчета используется квадрат таблицы.

Светлана Михайловна Математика 5-го класса, повторение

Доказательство формул сокращенного умножения

Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).

Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.

Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2. Докажем, что a2 — b2 = (a — b) * (a + b). Докажем, что a2 — b2 = (a — b) * (a + b)

Докажем, что a2 — b2 = (a — b) * (a + b).

Поехали:

1. Используя искусственный метод, прибавим и отнимем одно и тоже a * b.

   + a * b — a * b = 0

   a2 — b2 = a2 — b2 + ab — ab

1. Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
2. Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
3. Вынесем общие множители за скобки:

   (a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)

1. Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
2. Результат доказательства: a2 — b2 = (a — b) * (a + b)
3. Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.

Остальные ФСУ можно доказать аналогичным методом.

Таблица квадратов натуральных чисел 100 до 200

1012 = 10 2011022 = 10 4041032 = 10 6091042 = 10 8161052 = 11 0251062 = 11 2361072 = 11 4491082 = 11 6641092 = 11 8811102 = 12 100	1112 = 12 3211122 = 12 5441132 = 12 7691142 = 12 9961152 = 13 2251162 = 13 4561172 = 13 6891182 = 13 9241192 = 14 1611202 = 14 400	1212 = 14 6411222 = 14 8841232 = 15 1291242 = 15 3761252 = 15 6251262 = 15 8761272 = 16 1291282 = 16 3841292 = 16 6411302 = 16 900	1312 = 17 1611322 = 17 4241332 = 17 6891342 = 17 9561352 = 18 2251362 = 18 4961372 = 18 7691382 = 19 0441392 = 19 3211402 = 19 600	1412 = 19 8811422 = 20 1641432 = 20 4491442 = 20 7361452 = 21 0251462 = 21 3161472 = 21 6091482 = 21 9041492 = 22 2011502 = 22 500
1512 = 22 8011522 = 23 1041532 = 23 4091542 = 23 7161552 = 24 0251562 = 24 3361572 = 24 6491582 = 24 9641592 = 25 2811602 = 25 600	1612 = 25 9211622 = 26 2441632 = 26 5691642 = 26 8961652 = 27 2251662 = 27 5561672 = 27 8891682 = 28 2241692 = 28 5611702 = 28 900	1712 = 29 2411722 = 29 5841732 = 29 9291742 = 30 2761752 = 30 6251762 = 30 9761772 = 31 3291782 = 31 6841792 = 32 0411802 = 32 400	1812 = 32 7611822 = 33 1241832 = 33 4891842 = 33 8561852 = 34 2251862 = 34 5961872 = 34 9691882 = 35 3441892 = 35 7211902 = 36 100	1912 = 36 4811922 = 36 8641932 = 37 2491942 = 37 6361952 = 38 0251962 = 38 4161972 = 38 8091982 = 39 2041992 = 39 6012002 = 40 000

Скачать таблицу картинкой

Таблица квадратов натуральных чисел от $10$ до $99$

Другой популярной таблицей является таблица квадратов чисел от $10$ до $99$ (табл. 4), то есть всех десятичных чисел.

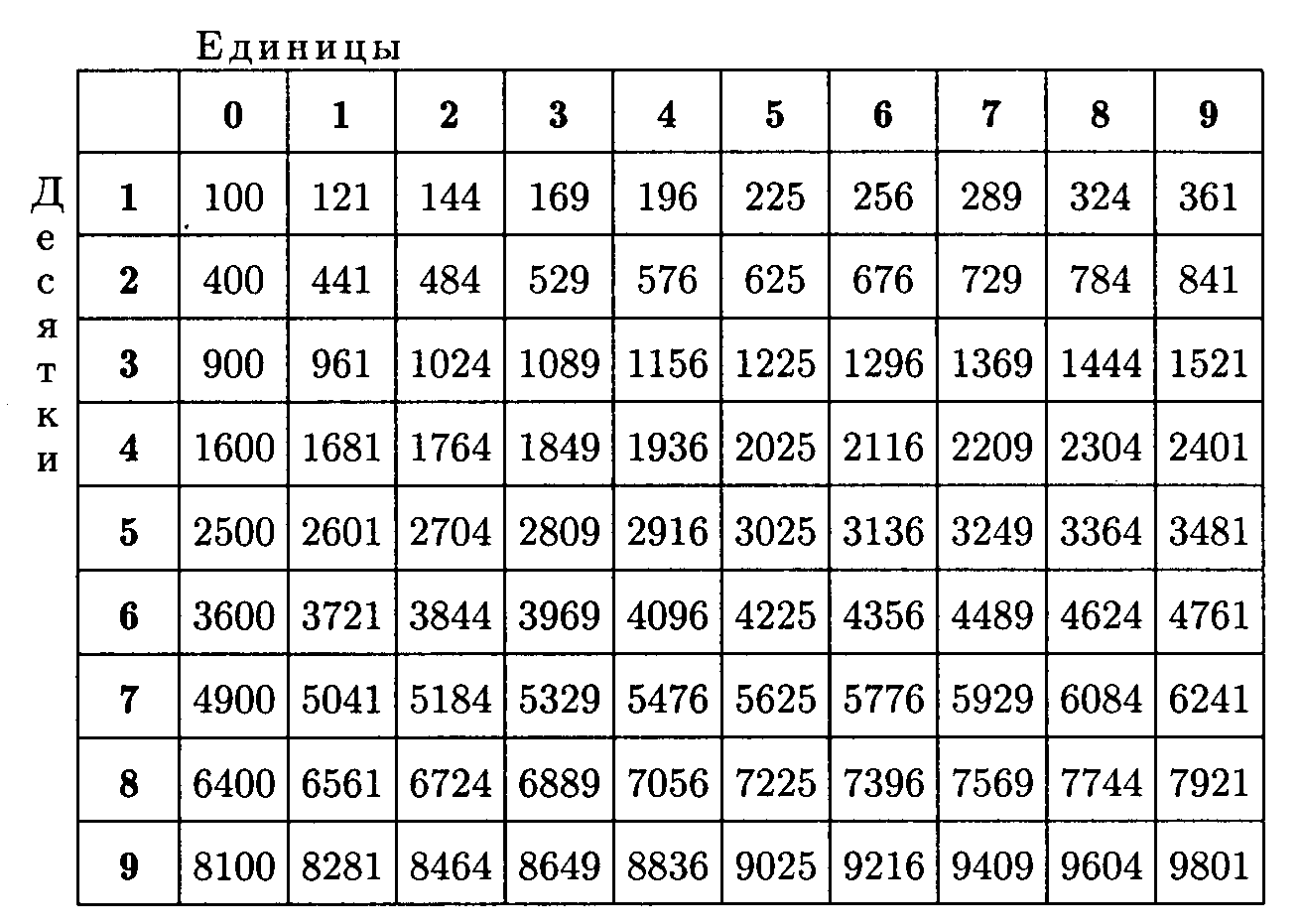
Необходимо найти значения из этой таблицы следующим образом: В первом столбце находим количество десятков интересующего нас числа. Запомните число в этой строке. Итак, в первом слагаемом находим количество единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца даст нам ответ.

Пример 3

Найдите $37^2$

Решение.

Находим число $3$ в первом столбце: получаем 4 строку.

Находим число $7$ в первой строке: получаем восьмой столбец.

Мы видим, что на их пересечении число $1369$. Поэтому

37$^2=1369$

Особенности использования для вычисления квадратов

Благодаря таблице можно выделить особенности квадрата целого числа.

1. Последняя цифра квадрата может быть равна 0, 1, 4, 5, 6 или 9. Квадрат не оканчивается цифрами 2, 3, 7 и 8.
2. Количество нулей на конце квадрата всегда четное.
3. Квадрат натурального числа либо делится на 4, либо при делении на 8 дает остаток 1.
4. Квадрат натурального числа либо делится на 9, либо при делении на 3 дает остаток 1.

Примеры возведения двухзначных и трехзначных чисел

Рассмотрим пример вычисления квадрата двузначного числа по таблице.

Задача 1

Вычислить (38^2).

Решение

Можно умножить число 38 на себя, а можно воспользоваться таблицей и сразу записать значение.

Ответ: (38^2;=;1444)

Рассмотрим пример решения геометрической задачи по теореме Пифагора.

Задача 2

Один из катетов прямоугольного треугольника равен 12. Другой катет равен 9. Найти гипотенузу.

Решение

Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. Исходя из таблицы, (12^2=144), а (9^2=81). Сумма квадратов катетов равна 225. Исходя из таблицы, (sqrt{225}=15).

Ответ: гипотенуза равна 15.

Существуют и расширенные таблицы, в том числе — для вычисления квадратов трехзначных чисел.

Задача 3

Вычислить квадрат числа 123.

Решение

Можно умножить число 123 на себя, а можно воспользоваться таблицей и сразу записать значение. Необходимо найти пересечение ряда 120 и столбца 3.

Таблица квадратов двузначных чисел

Чтобы вычислить квадрат двузначного числа, умножить число на самого себя. В результате получается уже четырехзначное число. Если при вычислении квадратов чисел до 10 достаточно вспомнить таблицу умножения, то посчитать квадрат двузначного числа в уме уже сложнее. Проще всего для таких вычислений использовать таблицу.

	1	2	3	4	5	6	7	8	9
1	100	121	144	169	196	225	256	289	324	362
2	200	441	484	529	576	625	676	729	784	841
3	300	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Как Пифагор рассчитывал способности человека

Квадрат Пифагора был добавлен на сайт In-contri по многочисленным просьбам пользователей нашего расчета совместимости, в котором в третьем разделе участвуют сравнения параметров двух партнеров из их психоматриц.

Несложно догадаться, что автором этого квадрата является, пожалуй, самый известный ученый, философ и математик — Пифагор. Его теорема известна каждому из нас со школьной скамьи, описанная им музыкальная гармония знакома всем, кто учился музыке, а его учение о познании мира стало основой всех естественных наук.

«Познать мир — значит познать управляющие им числа» — так утверждал Пифагор.

Одной из сфер его широкой научной деятельности было познание души человека и качеств изначально заложенных в личность через персональный расчет по дате рождения. Впоследствии этот расчет — квадрат Пифагора (он же психоматрица или магический квадрат) — стал одним из самых известных в нумерологии. Его целью являлось выявить данные человеку качества при рождении, чтобы направить его на тот путь, где бы он мог максимально раскрыть свои таланты, при этом уменьшив воздействие слабых сторон или компенсировав их.

Рассмотрим порядок расчета на примере:

Возьмем дату рождения 12.03.1985 (12 марта 1985 года).

1. Ищем сумму цифр дня и месяца из даты рождения:	1 + 2 + + 3 = 6
2. Складываем все цифры года из нашей даты:	1 + 9 + 8 + 5 = 23
3. Складываем полученные числа:	6 + 23 = 29 (1-е рабочее число)
4. Цифры из первого рабочего числа складываем между собой:	2 + 9 = 11 (2-е рабочее число)
5. Ищем разность первого рабочего числа и удвоенной первой цифры даты рождения:	29- 2*1 = 27 (3-е рабочее число)
6. Ищем сумму цифр из третьего рабочего числа:	2 + 7 = 9 (4-е рабочее число)

Делаем таблицу: первая строка — числа дня рождения в 8 ячеек, вторая строка — все рабочие числа тоже в 8 ячеек. Сразу замечание: если число дня рождения, месяца или рабочее число состоит из одной цифры, то оно все равно записывается в две ячейки, только первой будет ноль. В нашем случае это: 03 — март и 09 — 4 рабочее число.

1	2	3	1	9	8	5
2	9	1	1	2	7	9

Остается посчитать, сколько раз встречается каждая цифра в двух строках, и заполнить квадрат Пифагора. Расчет готов:

количество «1» 1111 характер	количество «4» — здоровье	количество «7» 7 удача
количество «2» 222 энергетика	количество «5» 5 логика, интуиция	количество «8» 8 доброта
количество «3» 3 познание	количество «6» — труд, рукоделие	количество «9» 99 память, ум

Уточнения:

● Если вы успели заметить, то для нашего времени цифр в расчете участвует 8 цифр: дата рождения 8 + 8 цифр из 4-х рабочих чисел — всего 16

● Если у человека день рождения или месяц рождения от 1 до 9, то записывается это в любом случае как две цифры, только первая будет 0 (а никак не пустой!)

● Многие онлайн расчеты грешат несоблюдением двух вышеназванных нюансов, поэтому вы можете встретить неправильные результаты

Рациональный интерьер для семьи с детьми

35 кв. м в фотографиях подтверждает, что можно жить с комфортом даже в стесненных условиях

Важно грамотно разделить личное пространство детей и взрослых

Часть зала, выполняющая функции спальни, можно отгородить встроенными шкафами с зеркалами или стеллажами с множественными полками, обращенными в детскую зону. На них разместятся книжки и игрушки, канцелярские принадлежности и другие мелкие предметы.

Общий вид комнаты для семьи с ребенком

Организация «детского» пространства

Детская зона отделена ширмой

Гостиная зона с встроенными светильниками на потолке

Если детей двое, лучше купить двухъярусную кровать, но младшего обычно укладывают снизу. Двухуровневая мебель подойдет и для неполной семьи, тогда мама отдыхает внизу, а ребенок охотно пользуется лесенкой, ведущей на кровать-чердак на шкафу.

Кресло-кровать и всевозможные мебельные трансформеры тоже будут полезны для экономии пространства. Хорошее решение – подиум для компьютерного стола, под которым скрывается выдвижная кровать.

Гостиная зона на подиуме с выдвижной кроватью

Для органичного решения любого проекта важно стилистическое соответствие. Это может быть классика или кантри, модерн или арт-деко, современные стили или что-то с этническим привкусом

Выбирайте любой дизайн-проект для своей однокомнатной квартиры 35 кв.м, используя фотографии из нашей подборки

Выбирайте любой дизайн-проект для своей однокомнатной квартиры 35 кв.м, используя фотографии из нашей подборки.

Квадраты чисел от 10 до 99

РАЗ	ЕДИНИЦЫ
	1	2	3	4	5	6	7	8	9
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764 г	1849 г	1936 г	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Как пользоваться таблицей:

Уровень в первом столбце, один в верхнем ряду. Квадрат определенного числа находится на пересечении искомых десятков и единиц.

Допустим, что нам нужно найти квадрат числа 45. В столбце десятков ищем число 4, в ряду единиц — число 5. Их пересечение соответствует числу 2025 — ответ, который мы хотели найти.

Выводы

Перед тем, как провести в доме проводку, обязательно ознакомьтесь с существующими разновидностями проводов. Электрики также рекомендуют перед покупкой изучить медный провод на цвет, поскольку производители могут экономить на материале и использовать сплав. Это способствует значительному увеличению электрического сопротивления, что, в свою очередь, не позволяет использовать допустимый уровень нагрузки для конкретного сечения.

Специалисты также советуют измерять при расчетах только жилу. Какой бы тонкой не была изоляция на проводе, каким бы гибким он ни был, для получения точных данных вам так или иначе придется ее устранять. Ведь в противном случае лишние миллиметры дадут вам повод применять для проводки недопустимо маленькое сечение провода, нагрузка для которого по итогу будет чрезмерной. Это, в свою очередь, чревато последствиями.