Как делить в столбик: пошаговый алгоритм

Как объяснить ребенку деление двузначного числа на однозначное не в столбик?

Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?

Возьмем для примера 72:3.

Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3: 72=30+30+12.

Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3. Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).

72:3=24Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.

После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

Особенности

Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .

Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:

1. Цифры.
2. Знаки арифметических действий.
3. Удаление раннее введенных символов.

Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.

Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:

• умножение;
• деление;
• сложение;
• вычитание.

Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.

Методика деления в столбик

Существует определенный алгоритм для деления в столбик. Изучается он в начальных классах средних образовательных школ. Методику можно применять не только для положительных, но и отрицательных значений. При этом нужно учитывать знак:

1. Деление отрицательной величины на отрицательную — положительное значение.
2. При делении положительного на отрицательное или наоборот — отрицательная величина.

Алгоритм без остатка

Методика применяется в том случае, когда делимое является не простым числом, а содержит множители. Кроме того, при его делении на делитель, не соответствующий одному из признаков деления. Например, 33 делится на 2 с остатком. Однако, когда делитель равен 3, то последнего нет.

Для применения алгоритма нужно наглядно разобрать следующий пример: требуется разделить 78 на 2. Методика выполнения этой операции имеет следующий вид:

1. Записать делимое с левой стороны, а делитель — справа.
2. По карточке простых чисел или при помощи ручного метода необходимо определить принадлежность делимого к простым значениям (78 делится на 2, поскольку заканчивается на четную цифру 8).
3. Разделить две значения вертикальной чертой.
4. Выделить I неполное делимое: 7.
5. По таблице умножения подобрать ближайшее целое (3). При произведении его на делитель должно получиться значение, которое меньше первого неполного делимого (3 * 2 = 6 < 7). Если записать 4, то 4 * 2 = 8 > 7 (вариант не подходит).
6. Записать число, полученное при умножении делителя на подобранное значение, под I неполным делимым. Произвести операцию вычитания (7 — 6 = 1).
7. Результат вычитания (1), который называется остатком, не делится на 2. Следовательно, нужно дописать II неполное делимое (18). Если по какой-то причине, результат делится на делитель, то подобранное значение является неверным.
8. Значение 18 делится на 2, т. е. 18/2 = 9.
9. Результат деления 78 на 2 равен 39.

Операция с остатком

Не во всех случаях результат деления двух чисел является целой величиной. В школьной программе встречается группа примеров, в которых требуется найти остаток, полученный при выполнении операции деления 2 значений (77/3). Алгоритм похож на предыдущий, но имеются некоторые особенности:

1. Два числа записываются, как и в предыдущем случае.
2. Принадлежность к множеству простых чисел не проверяется.
3. Выделить I неполное делимое: 7.
4. Подобрать ближайшее целое число, записав его в результат: 2.
5. Выполнить проверку: 3 * 2 = 6 < 7 (значение подходит).
6. Записать 6 под 7, а затем выполнить операцию вычитания: 7 — 6 = 1. Остаток меньше 3, следовательно, число подобрано правильно.
7. Выполнить подбор множителя для 17: целочисленного значения нет. Следовательно, нужно подобрать ближайшее целое: 5.
8. Произвести проверку: 3 * 5 = 15 < 17.
9. Записать 5 в результат и определить остаток: 17 — 15 = 2.
10. Результат деления 77 на 3 эквивалентен: 25 с остатком 2.

Таким образом, для выполнения операции деления двузначного числа на однозначное нужно знать признаки делимости величин, а также основные алгоритмы деления с остатком и без него.

Алгоритм деления столбиком

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4 · 0 = 0 14 ; 4 · 1 = 4 14 ; 4 · 2 = 8 14 ; 4 · 3 = 12 14 ; 4 · 4 = 16 > 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .

Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2 ; 4 · 1 = 4 > 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9 .

После второго, третьего и четвертого шага алгоритма запись примет вид:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7 .

Работа с многозначными числами

Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами свыше 100.

Данное действие удобнее всего выполнять в столбик, так как НЧ также будет двузначным (в большинстве случаев), а алгоритм столбика облегчает подсчет и делает его более наглядными.

Разделим многозначные числа на двузначные: 386:25

Данный пример отличается от предыдущих количеством уровней расчета, хотя подсчет проводят по тому же принципу, что и ранее. Рассмотрим подробнее:

386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить ост-к.

Первый уровень

Делитель – двузначное число. Делимое – трехзначное. Выделяем у последнего первые две левые цифры – это 38. Сравниваем их с делителем. 38>25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?

25*1=25, 25*2=50. 50>38, возвращаемся на один шаг назад.

Ответ – 1. Вписываем единицу в зону не полного частного.

Далее:

38-25=13. Вписываем 13 под чертой.

Второй уровень

25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150>136 – возвращаемся назад на один шаг. Добавляем цифру 5 в зону неполного частного, справа от единицы.

Определяем остаток:

136-125=11. Приводим под чертой. 11>25? Нет – действие провести нельзя. У делимого не остались цифры. Значит, делить больше нечего. Подсчет закончен.

Ответ: НЧ равно 15, в ост-ке 11.

Если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого, то в таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в подсчете сразу.

Приведем примеры на деление с трех- и четырехзначными числами:

386:75

75 – двузначное. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38>75? Нет – деление провести нельзя. Берем все 3 цифры. 386>75? Да – действие провести можно. Проводим расчет.

75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450>386 – возвращаемся на шаг назад. Вписываем 5 в зону неполного частного.

Находим остаток: 386-375=11. 11>75? Нет. Также не остались цифры у делимого. Подсчет закончен.

Результат: НЧ = 5, в ост-ке — 11.

119:35

Выполняем проверку: 11>35? Нет – математическую операцию провести нельзя. Подставляем третье число – 119>35? Да – действие провести можем.

35*1=35, 35*2=70, 35*3=105, 35*4=140. 140>119 – возвращаемся на один шаг назад. Вписываем 3 в зону неполного ост-ка.

Результат: НЧ = 3, осталось — 14.

1195:99

Проверяем: 11>99? Нет – подставляем еще одну цифру. 119>99? Да – начинаем вычисления.

11<99, 119>99.

99*1=99, 99*2=198 – перебор. Вписываем 1 в неполное частное.

Находим ост-к: 119-99=20. 20<99. Опускаем 5. 205>99. Вычисляем.

99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.

Находим ост-к: 205-198=7.

Результат: НЧ = 12, остаток — 7.

Деление с остатком — примеры:

Учимся делить в столбик с остатком:

Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно. Этой теме необходимо уделить больше внимания, чтобы разобраться со всеми тонкостями подсчета. В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет. 

Как выполнить длинное деление на одно число

В старые времена очень важно было уметь делить большие числа. Базовое деление в длинных по-прежнему полезно знать, поэтому следующие примеры покажут вам, как разделить однозначный делитель на другое число, а затем как найти остаток

Вспомните, что делитель в задаче на деление — это число, на которое вы делите. Когда вы выполняете деление в длинные числа, вас больше всего беспокоит размер делителя: с маленькими делителями работать легко, а с большими — сплошная головная боль. Итак, здесь вы будете работать с красивым маленьким делителем, состоящим из одной цифры. Предположим, вы хотите найти 860. 5. Начните с написания задачи следующим образом:

В отличие от других операций «Большой четверки», длинное деление движется слева направо.

Вычтите 8–5, чтобы получить 3. (Примечание: после вычитания результат всегда должен быть меньше делителя. Если нет, вам нужно написать большее число над знаком деления.) Затем опустите 6, чтобы получилось новый номер 36:

Эти шаги представляют собой один полный цикл, и для завершения задачи вам просто нужно их повторить. Теперь спросите, сколько раз 5 входит в число 36, то есть сколько будет 36 5? Ответ 7 (с небольшим остатком). Напишите 7 чуть выше 6, а затем умножьте 7 на 5, чтобы получить 35; напишите ответ под 36:

Теперь вычтите, чтобы получить 36 – 35 = 1; уменьшите 0 рядом с 1, чтобы сделать новое число 10:

Еще один цикл завершен, поэтому начните следующий цикл, спросив, сколько раз 5 переходит в 10, то есть 10 5.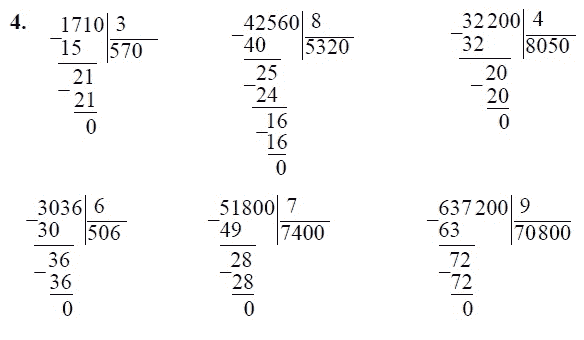

Теперь вычтите 10 – 10 = 0. Поскольку у вас больше нет чисел, которые нужно записывать, вы закончили, и вот ответ (то есть частное):

Итак, 860 5 = 172.

Эта задача делится поровну, но не многие. Следующие инструкции расскажут вам, что делать, когда у вас закончились номера, которые нужно сбить.

Деление отличается от сложения, вычитания и умножения тем, что возможно наличие остатка. Остаток — это просто часть, оставшаяся от деления.

Буква r указывает, что число, следующее за ним, является остатком.

Например, предположим, что вы хотите разделить семь шоколадных батончиков между двумя людьми, не разбив ни одного шоколадного батончика на кусочки (слишком беспорядочно). Таким образом, каждый человек получает три шоколадных батончика, и один шоколадный батончик остается. Эта проблема показывает вам следующее:

7 2 = 3 с остатком 1 или 3 r 1

В длинном делении остаток — это число, которое останется, когда у вас больше не будет чисел, которые нужно заносить.

Обратите внимание, что когда вы выполняете деление с небольшим делимым и большим делителем, вы всегда получаете частное 0 и остаток от числа, с которого вы начали:

1 2 = 0 р 1

14 23 = 0 р 14

2000 2001 = 0 r 2000

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.

Пошаговая инструкция обучения делению столбиком

Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8. Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211. Результат необходимо перепроверить обратным умножением.

В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:

• Берем первую цифру числа, делим ее на делитель. Сколько раз делитель может содержаться в делимом?
• Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
• Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.
• Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
• Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.

На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.

Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки. В школе эти действия изучаются от простого к сложному

Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Запись чисел при делении столбиком

Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:

Пусть нам нужно разделить 6105 на 55 , запишем:

Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:

Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.

Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:

Деление в столбик – правила

Для того, чтобы уметь делить в столбик необходимо знать некоторые правила. Именно об этом и пойдет далее речь. Ведь деление в столбик невозможно освоить если не знать элементарного – таблицы умножения. Считать простые примеры на умножение необходимо быстро и в уме. Это только в начале обычно дети пользуются черновиками, чтобы подобрать множитель, таким образом найти частное. Еще надобно уметь разбивать числа на сотни, десятки, тысячи – не путаться и в этих понятиях. Для наглядности, где делимое, где делитель, где частное можете изучить термины на изображении ниже.

Что нужно знать для деления в столбик?

Прежде, чем приступать к делению, следует проверить ребенка на знания элементарных правил. Ведь пропускать математику нельзя. А если пропуски все же были, то нужно изучить тот материал, что изучали ранее на уроках в школе

Понадобится обратить внимание на такие знания, как:

Запомнил ли школьник, как называются все элементы, участвующие в процессе деления.

Обратите внимание на знание таблицы умножения ребенком. Еще ребенок должен усвоить, какие бывают разряды числа (единицы, десятки, сотни)

Пример: 

1. 57: 3, где 57 – это делимое, число, что разделяют на доли, а 3 – это делитель, указывающий, на сколько делить предыдущее число.
2. Определяемся, вначале какие единицы выделить в делимом для осуществления деления в столбик числа 57. Число 5 > 3.
3. Узнайте, сколько раз следует взять число 3, чтобы получить 5. Результат 3 · 1 = 3 ≤ 5. Значит подходит и 1 поставьте в качестве первой цифры частного.
4. Теперь вычитание: 5 — 3 = 2. Остаток 2 и единицу сносим, выходит 27.
5. Находим теперь, на какое число нужно умножить 3, чтобы результат был 27. Согласно таблице умножения 3 · 9 = 27.
6. Итого результат 19.

Умножение, деление – взаимосвязаны между собой, хотя и противоположные операции. Чтобы проверить, верно ли нашли частное, необходимо выполнить умножение. Потому таблица умножения и умение умножать на черновике без калькулятора всегда пригодится ребенку, также еще при умножении следует уметь правильно прибавлять, а при делении в столбик вычитать. В математики все действия с числами между собой взаимосвязаны.

Ниже смотрите пример деления в столбик 536 на 4. Действия с трехзначным делимым выполняются аналогично, что и с двухзначным.

Деление

Деление в школе начинают учить уже с третьего класса. Школьники только изучают азы процесса, выполняют самые простые примеры на это действие.

Примеры подобны умножению, только детей учат таблице деления, а не умножения. Школьники должны уловить саму суть, что означает поделить число на несколько частей, изучают, что такое делимое, делитель, частное. Узнают, как проверить умножением правильность решения примера или же задачи. В столбик дети еще не считают, так как даются самые простые примеры и все числа из таблицы умножения. Пример: 81 : 9 = 9.

Процесс деления в четвертом классе значительно усложняется. Детям дают вначале года вспомнить, что они учили в третьем классе, а далее уже начинают осваивать технику деления чисел в столбик. Именно за этот учебный год осваивают такие знания. Ниже приведен алгоритм решения примеров в столбик с подробным описанием процесса.

Здесь даже учтено то, что возможно будет остаток при делении, что число получится не цельным, а через запятую.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому. Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

14:3

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Как делить столбиком

Допустим, нам нужно разделить  780  на  12,  записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число  7,  так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число  78  больше делителя, поэтому мы начинаем деление с него:

В нашем случае число  78  будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра —  0,  это значит, что частное будет состоять из  2  цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз  12  содержится в числе  78.  Для этого мы последовательно умножаем делитель на натуральные числа  1, 2, 3, …,  пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число  6,  записываем его под делитель, а из  78  (по правилам вычитания столбиком) вычитаем  72  (12 · 6 = 72).  После того, как мы вычли  72  из  78,  получился остаток  6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше

К получившемуся остатку —  6,  сносим следующую цифру делимого —  0.  В результате, получилось неполное делимое —  60.  Определяем, сколько раз  12  содержится в числе  60.  Получаем число  5,  записываем его в частное после цифры  6,  а из  60  вычитаем  60  (12 · 5 = 60).  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит  780  разделилось на  12  нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

780 : 12 = 65.

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить  9027  на  9.

Определяем неполное делимое — это число  9.  Записываем в частное  1  и из  9  вычитаем  9.  В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого —  0.  Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль  (0 : 9 = 0)  и в промежуточных вычислениях из  0  вычитаем  0.  Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого —  2.  В промежуточных вычислениях вышло так, что неполное делимое  (2)  меньше, чем делитель  (9).  В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз  9  содержится в числе  27.  Получаем число  3,  записываем его в частное, а из  27  вычитаем  27.  В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число  9027  разделилось на  9  нацело:

9027 : 9 = 1003.

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить  3000  на  6.

Определяем неполное делимое — это число  30.  Записываем в частное  5  и из  30  вычитаем  30.  В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого —  0.  Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из  0  вычитаем  0:

Сносим следующую цифру делимого —  0.  Записываем в частное ещё один нуль и в промежуточных вычислениях из  0  вычитаем  0.  Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток —  0.  Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит  3000  разделилось на  6  нацело:

3000 : 6 = 500.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

рисунок из презентации на тему деления трёхзначного числа столбиком

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

пример деления трехзначного числа на однозначное столбиком

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

примеры деления столбиком трехзначных чисел на двузначные

Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

пример деления в столбик трёхзначного числа на трёхзначное с остатком