Аналитическая геометрия/векторы и действия над ними

Направляющие косинусы вектора

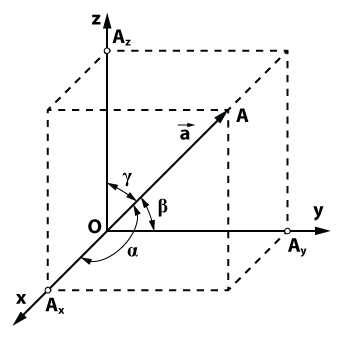
Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех
его измерений. Следовательно,
\(|OA|^2 = |OA_x|^2 + |OA_y|^2 + |OA_z|^2 \)
Но \(|OA| = |\vec{a}|, \;\; |OA_x| = |X|, \;\; |OA_y| = |Y|, \;\;|OA_z| = |Z| \); таким образом, получаем
\(|\vec{a}|^2 = X^2 + Y^2 + Z^2 \)
или
\(|\vec{a}| = \sqrt{X^2 + Y^2 + Z^2} \)
Эта формула выражает длину произвольного вектора через его координаты.

Обозначим через \(\alpha, \; \beta, \; \gamma \) углы между вектором \(\vec{a} \) и осями координат. Из формул проекции вектора на
ось и длины вектора получаем
\(\cos \alpha = \frac{X}{\sqrt{X^2 + Y^2 + Z^2}} \)
\(\cos \beta = \frac{Y}{\sqrt{X^2 + Y^2 + Z^2}} \)
\(\cos \gamma = \frac{Z}{\sqrt{X^2 + Y^2 + Z^2}} \)
\(\cos \alpha, \;\; \cos \beta, \;\; \cos \gamma \) называются направляющими косинусами вектора \(\vec{a} \)
.

Возводя в квадрат левую и правую части каждого из предыдущих равенств и суммируя полученные результаты, имеем
\(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1 \)
т.е. сумма квадратов направляющих косинусов любого вектора равна единице.

Проекции векторов на прямую и на плоскость

Пусть на плоскости задана прямая Проекцией вектора , началом которого служит проекция , начала конца . Проекцией вектора (вдоль плоскости ) называется вектор , началом которого служит проекция , начала конца перпендикулярна прямой

Проекция вектора на плоскость

Пусть в пространстве задана плоскость я и пересекающая ее прямая . Проекцией вектора параллельно прямой , началом которого служит проекция начала конца , то проекция называется ортогональной.

Свойства проекций векторов

1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.

2. Проекции равных векторов равны.

3. Проекция суммы векторов равна сумме их проекций.

4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).

5. Проекция линейной комбинации векторов равна линейной комбинации проекций.

Рассмотрим эти свойства для проекций векторов на прямую — проекция вектора — проекция вектора , т.е. проекции одного и того же вектора

Докажем второе свойство. Пусть на плоскости даны равные векторы и . Из равенства следует, что четырехугольник — параллелограмм, а треугольники и равны по стороне и двум прилежащим углам

Пятое свойство проекций следует из третьего и четвертого.

Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).

1. Если на плоскости заданы две пересекающиеся прямые и , то любой вектор и на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. .

2. Если в пространстве заданы три прямые и , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. .

В самом деле, пусть прямые и пересекаются в точке . По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство , которое равносильно доказываемому равенству , так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.

Если же вектор , то соответствующие проекции имеют вид: и равенство , очевидно, выполняется.

Аналогично доказывается второе утверждение.

Справедливы утверждения, обратные к указанным в теореме 1.1.

Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. , то слагаемые и являются проекциями вектора и соответственно.

Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. , то слагаемые и являются проекциями вектора соответственно.

В самом деле, отложим от произвольной точки (рис.1.19,6). Тогда из равенства следует, что , т.е. вектор — является диагональю параллелепипеда, построенного на векторах (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому — проекции вектора на прямые (проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые). Так как равные векторы имеют равные проекции (свойство 2), заключаем, что проекции вектора равны соответственно. Наконец, проекции на прямые равны проекциям на параллельные им прямые, содержащие векторы соответственно.

Пример 1.5. Если прямая пересекает стороны треугольника (или их продолжения) в точках соответственно, то

Решение. Найдем отношения проекций векторов на прямую вдоль прямой (рис. 1.20). Для этого через точку , параллельную прямой . По свойству 4 проекций имеем:

Перемножая эти пропорции, получаем , что равносильно доказываемому равенству.

Заметим, что доказанное утверждение является частью теоремы Менелая.

Пример 1.6. Если на сторонах треугольника взяты соответственно точки так, что прямые пересекаются в одной точке, то

Решение. Пусть прямые пересекаются в точке (рис.1.21). Через точку проведем прямые и параллельно и соответственно. По свойству проекций (свойство 4):

Учитывая эти равенства и свойства отношений коллинеарных векторов (см, разд.1.2.1), преобразуем левую и правую части последнего равенства:

Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:

Понятие вектора. Свободный вектор

Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка , концом отрезка – точка . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.

!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении  и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: , но допустима и запись , которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе

В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: , подразумевая тем самым, что это вектор.

То была стилистика, а сейчас о способах записи векторов:

1) Векторы можно записать двумя большими латинскими буквами: и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

2) Векторы также записывают маленькими латинскими буквами: В частности, наш вектор  можно для краткости переобозначить маленькой латинской буквой .

Длиной или модулем ненулевого вектора  называется длина отрезка . Длина нулевого вектора  равна нулю. Логично.

Длина вектора обозначается знаком модуля: ,

Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки:

Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной «школьный» вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё почти корректно – направленный отрезок можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)

Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия. Впрочем, несвободные векторы встречаются и в курсе вышмата (не ходите туда :)).

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора  и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор  от конца вектора :

Суммой векторов  и  является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов  представляет собой вектор результирующего перемещения  с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор  отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация:  (векторы сонаправлены) или  (векторы направлены противоположно).

Произведением ненулевого вектора  на число  является такой вектор , длина которого равна , причём векторы   и  сонаправлены при  и противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка:

Разбираемся более детально:

1) Направление. Если множитель  отрицательный,  то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах  или , то длина вектора уменьшается. Так, длина вектора  в два раза меньше длины вектора . Если множитель  по модулю больше единицы, то длина вектора увеличивается в  раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно  коллинеарны

Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы  сонаправлены. Векторы  и  также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Правило параллелограмма

По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.

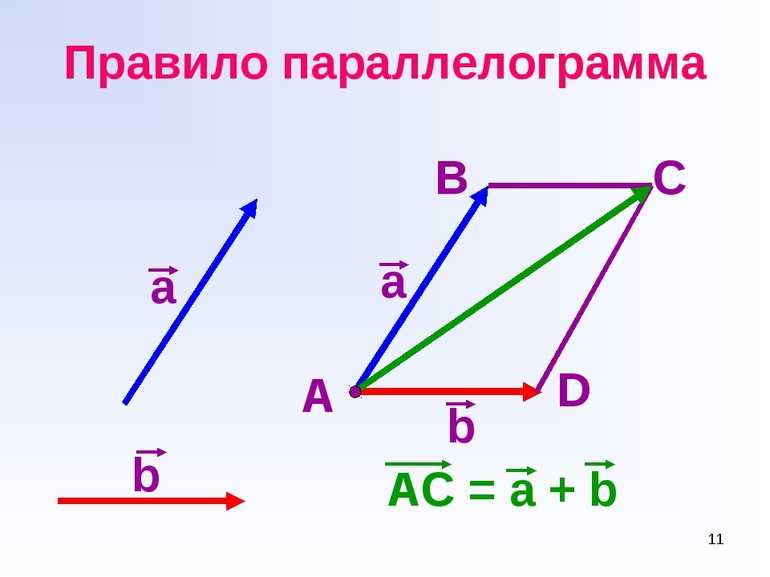
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.

Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.

Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.

8 Разложение вектора по двум неколлинеарным векторам

Любой
вектор

единственным образом разлагается на плоскости по двум неколлинеарным
ненулевым векторам

и

с единственными коэффициентами разложения x
и y:

=
x

+ y

Любой
вектор

,
компланарный ненулевым неколлинеарным векторам

и

,
единственным образом разлагается по этим двум векторам

и

с единственными коэффициентами разложения x
и y:

=
x

+ y

Разложим
на плоскости заданный ненулевой вектор

по данным ненулевым неколлинеарным векторам

и

:

Если
векторы

,

и

компланарные, то на плоскости проведем их из одной точки, построив
векторы равные заданным компланарным векторам

Из
конца вектора

проведем прямые, параллельные векторам

и

до пересечения с прямыми, проведенными через вектора

и

.
Получим параллелограмм

Длины
сторон параллелограмма получаются путем умножения длин векторов

и

на числа x и y,
которые определяются путем деления длин сторон параллелограмма на
модули (длины) соответствующих им векторов

и

.
Получаем разложение вектора

по заданным неколлинеарным векторам

и

:

=
x

+ y

В
решаемой задаче x ≈ 1,3, y
≈ 1,9, поэтому разложение вектора

по заданным неколлинеарным векторам

и

можно записать в виде

=
1,3

+ 1,9
.

Разложим
на плоскости заданный ненулевой вектор

по данным ненулевым неколлинеарным векторам

и

:

В
решаемой задаче x ≈ 1,3, y
≈ -1,9, поэтому разложение вектора

по заданным неколлинеарным векторам

и

можно записать в виде

=
1,3

— 1,9
.

Пример задачи на понятие разности векторов

Пример 2

Пусть дан параллелограмм $ADCD$, диагонали которого пересекаются в точке $O$. $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AD}=\overrightarrow{b}$ (рис. 4). Выразить через векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ следующие векторы:

а) $\overrightarrow{DC}+\overrightarrow{CB}$

б) $\overrightarrow{BO}-\overrightarrow{OC}$

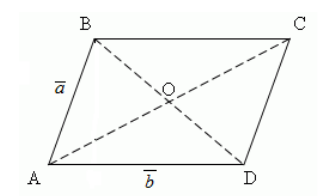Рисунок 4. Параллелограмм

Решение.

а) Произведем сложение по правилу треугольника, получим

\

Из первого правила разности двух векторов, получаем

\

б) Так как $\overrightarrow{OC}=\overrightarrow{AO}$, получим

\

По теореме 2, имеем

\

Используя правило треугольника, окончательно имеем

\

Теорема (о вычислении проекции вектора через косинус)

Проекция ненулевого вектора на ось равна длине этого вектора, умноженной на косинус угла между этим вектором и осью.

Доказательство

Пусть дан вектор $\vec{v}=\overrightarrow{AB}\neq\vec{0}$, $\vec{e}$ – единичный вектор координатной оси $x$, и $\varphi=\angle(\vec{v}, \vec{e})$.

Докажем, что проекция $v_x$ вектора $\vec{v}$ на ось $x$ вычисляется по формуле $v_x=|\vec{v}|\cos{\varphi}$ $(1)$.

Возможны следующие случаи:

1) Угол $\varphi = 0^\circ$. Тогда $\overrightarrow{AB}=\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=|\vec{v}|$. Так как $\cos{0^\circ}$=1, то $v_x=|\vec{v}|\cos{\varphi}$.

2) Угол $\varphi$ острый. Пусть точка $A$ не лежит на оси $x$. Через точку $A$ проведем прямую $p$, параллельную оси $x$. Пусть точка $C$ – проекция точки $B$ на прямую $p$. Получим прямоугольный треугольник $ABC$ с углом $\varphi$ при вершине $A$ и прямоугольник $AA_1B_1C$. Тогда $v_x=|\overrightarrow{A_1B_1}|=AC=AB\cos{\varphi}=|\vec{v}|\cos{\varphi}$, то есть $v_x=|\vec{v}|\cos{\varphi}$.

Если точка $A$ лежит на оси $x$? то равенство $(1)$ вытекает из прямоугольного треугольника $ABB_1$.

3) Угол $\varphi=90^\circ$. В этом случае $\overrightarrow{AB}=\vec{e}$, $A_1=B_1$ и $v_x=0$. И так как $\cos{90^\circ}=0$, то равенство $(1)$ выполняется.

4) Угол $\varphi$ тупой. Сначала через точку $A$ проводим прямую $p$, параллельную оси $x$, и проецируем на нее точку $B$ в точку $C$юСнова получим прямоугольный треугольник $ABC$. Его угол при вершине $A$ равен $180^\circ-\varphi$. Поэтому $AC=AB\cos{(180^\circ-\varphi)}=-AB\cos{\varphi}$. В рассматриваемом случае $\overrightarrow{A_1B_1}\updownarrows\vec{e}$, и поэтому $v_x=-|\overrightarrow{A_1B_1}|=-AC=AB\cos{\varphi}=|\vec{v}\cos{\varphi}|$, то есть снова выполняется равенство $(1)$.

Если же точка $A$ лежит на прямой $x$ то доказательство только упрощается соответственным образом.

5) Угол $\varphi=180^\circ$. Тогда $\overrightarrow{AB}\updownarrows\vec{e}$, $\overrightarrow{A_1B_1}=\overrightarrow{AB}=\vec{v}$ и $v_x=-|\vec{v}|$. Так как $\cos{180^\circ}=-1$, то равенство $(1)$ снова имеет место.

Свойство 1

Равные векторы имеют равные проекции на заданную ось.

Доказательство

Проекция вектора $\vec{v}$ зависит лишь от длины этого вектора и угла $\varphi$, который он образует с данной осью, так как $v_x=|\vec{v}|\cos{\varphi}$. Равные же векторы имеют, во-первых, равные длины и, во-вторых, образуют с осью один и тот же угол (в силу параллельности прямых). Следовательно, их проекции равны.

Свойство 2

При сложении векторов их проекции на ось складываются.

Доказательство

Сложим любые два вектора $\vec{a}=\overrightarrow{AB}$ и $\vec{b}=\overrightarrow{BC}$. Получим вектор $\vec{c}=\vec{a}+\vec{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$. Пусть точки $A_1, B_1, C_1$ – проекции точек $A, B, C$ на ось $x$, а $x_A, x_B, x_C$ – их координатыб и $a_x, b_x, c_x$ – проекции векторов $\vec{a}, \vec{b}, \vec{c}$ на ось $x$.

Так как $a_x=x_B-x_A, b_x=x_C-x_B$, то $a_x+b_x=x_B-x_A+x_C-x_B=x_C-x_A$.

C другой стороны $c_x=x_C-x_A$.

Поэтому $c_x=a_x+b_x$.

Свойство 3

При умножении вектора на число его проекция умножается на это число.

Доказательство

Пусть $x$ – ось с начальной точкой $O$ и единичным вектором $\vec{e}$. Возьмем любой вектор $\vec{a}$ и отложим его от точки $O$: $\overrightarrow{OA}=\vec{a}$. Пусть $\varphi$ – угол между векторами $\vec{a}$ и $\vec{e}$. Умножим вектор $\vec{a}$ на число $\alpha$. Получим вектор $\vec{b}=\overrightarrow{OB}=\alpha\vec{a}$. Необходимо доказать, что $b_x=\alpha a_x$.

Возможны следующие случаи:

1) $\alpha>0$. Тогда $\angle(\vec{b},\vec{e})=\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=\alpha OA$. Поэтому $b_x=|\vec{b}|\cos{\varphi}=OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

2) $\alpha<0$. Тогда $\angle(\vec{b},\vec{e})=180^\circ-\varphi$. Кроме того, $|\vec{b}|=|\alpha||\vec{a}|$, то есть $OB=|\alpha| OA$. А так как $\alpha<0$, то $|\alpha|=-\alpha$ и поэтому $OB=-\alpha OA$. Следовательно, $b_x=|\vec{b}|\cos{(180^\circ-\varphi)}=-OB\cos{\varphi}=\alpha OA\cos{\varphi}=\alpha a_x$.

3) $\alpha=0$. Тогда $\vec{b}=\alpha \vec{a}=\vec{0}$, и поэтому $b_x=0$ и $b_x=\alpha a_x$.

Проекция линейной комбинации векторов, равна соответствующей линейной комбинации проекций этих векторов.

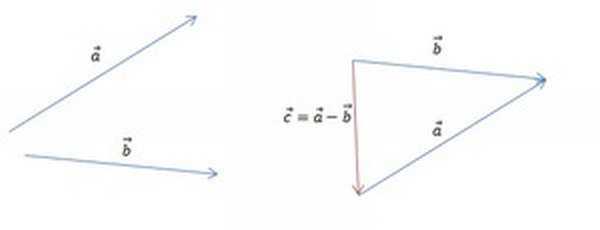
Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

1. По заданным координатам построить векторы, для которых нужно найти разность.
2. Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
3. Соединить начала обоих направленных отрезков и указать направление, результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.

Результат операции вычитания показан на рисунке ниже.

Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

1. Построить исходные направленные отрезки.
2. Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок, затем совместить его начало с уменьшаемым.
3. Построить сумму: соединить начало первого отрезка с концом второго.

Результат такого решения изображён на рисунке:

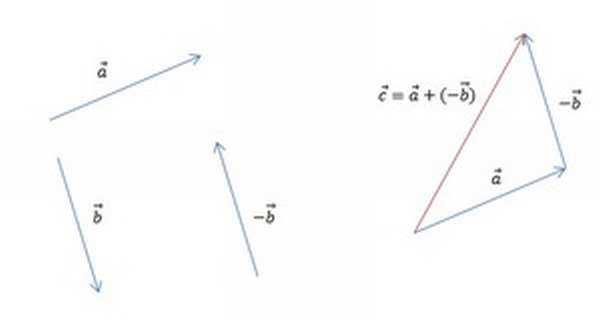
Линейные операции над геометрическими векторами

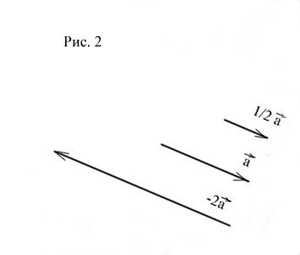
Умножение вектора на число

Произведением вектора на число
называется вектор, получающийся из вектора растяжением
(при ) или сжатием (при )
в раз, причём направление вектора
сохраняется, если ,
и меняется на противоположное, если . (Рис. 2)

Из определения следует, что векторы и =
всегда расположены на одной или на параллельных прямых. Такие векторы называются коллинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить «коллинеарны».) Справедливо и обратное утверждение:
если векторы и коллинеарны,
то они связаны отношением

.   (1)

Следовательно, равенство (1) выражает условие коллинеарности двух векторов.

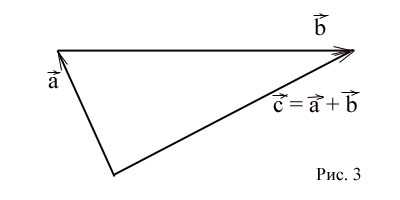
Сложение и вычитание векторов

При сложении векторов нужно знать, что суммой векторов и
называется вектор , начало которого
совпадает с началом вектора , а конец — с концом вектора ,
при условии, что начало вектора приложено к концу вектора . (Рис. 3)

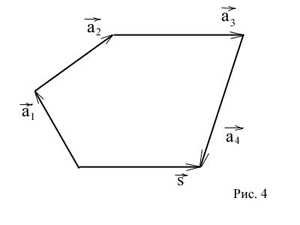
Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n
свободных векторов . При сложении
нескольких векторов за их сумму принимают замыкающий вектор, начало которого
совпадает с началом первого вектора, а конец — с концом последнего вектора. То есть, если к концу вектора
приложить начало вектора , а к концу вектора
— начало вектора и т.д. и, наконец, к концу вектора
— начало вектора , то
суммой этих векторов служит замыкающий вектор , начало которого совпадает с началом первого вектора
, а конец — с концом последнего вектора . (Рис. 4)

Слагаемые называются составляющими вектора , а
сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.

При умножении вектора на число -1 получается противоположный вектор
.
Векторы и имеют одинаковые длины и противоположные направления.
Их сумма даёт нулевой вектор,
длина которого равна нулю. Направление нулевого вектора не определено.

В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора
вектор
означает прибавить к вектору противоположный вектор
, т.е.

Пример 1. Упростить выражение:

.

Решение:

,

то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности,
также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед
вычислением произведений векторов.

Пример 2. Векторы и
служат диагоналями параллелограмма ABCD (рис. 4а).
Выразить через и
векторы , ,
и ,
являющиеся сторонами этого параллелограмма.

Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам.
Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости
от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат —
требуемые в условии задачи векторы:

Есть все основания полагать, что теперь Вы правильно ответили на вопрос о векторах «Предприимчивость»
и «Инновационные способности» в начале этого урока. Правильный ответ: над этими векторами производится
операция сложения.

Решить задачи на векторы самостоятельно, а затем посмотреть решения

Пример 3. Даны векторы
и
. Построить на
чертеже векторы 1) ,
2) ,
3) ,
4) .

Пример 4. Даны векторы
и
. Построить на
чертеже векторы 1) ,
2) ,
3) ,
4) .

Как найти длину суммы векторов?

Эта задача занимает особое место в операциях с векторами, так как
предполагает использование тригонометрических свойств. Допустим, Вам попалась задача
вроде следующей:

Даны длины векторов
и длина суммы этих векторов .
Найти длину разности этих векторов .

Решения этой и других подобных задач и объяснения, как их решать — в
уроке «Сложение векторов: длина суммы векторов и теорема косинусов».

А проверить решение таких задач можно на Калькуляторе
онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».

А где произведения векторов?

Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1, —3), B (0, 4), C (5, 8), D (—3, 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1, —3), а концом B (0, 4). Рассчитаем координаты направленного отрезка:

AB {0 — 1, 4 — (— 3)} = {— 1, 7}

Аналогичный расчёт выполняется для CD:

CD {— 3 — 5, 2 — 8} = {— 8, — 6}

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁, c₂} = {a₁ b₁, a₂ b₂}. Для конкретного случая можно записать:

q = {— 1 — 8, 7 — ( — 6)} = { — 9, — 1}

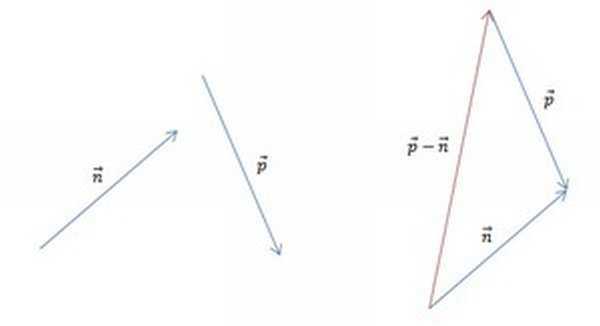
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n, m — n, m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

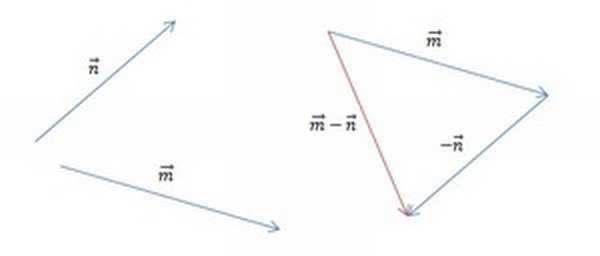Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

• m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m,
• (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p,
• (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

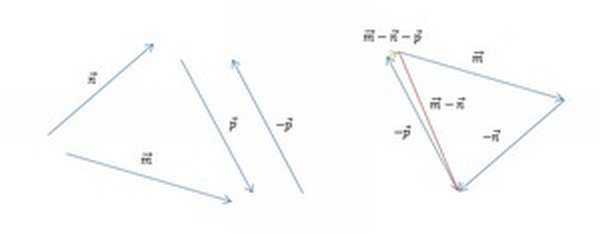
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.

Свойства операций над векторами.

Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов и произвольных действительных чисел можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.

1. Свойство коммутативности .
2. Свойство ассоциативности сложения .
3. Существует нейтральный элемент по сложению, которым является нулевой вектор , и . Это свойство очевидно.
4. Для любого ненулевого вектора существует противоположный вектор и верно равенство . Это свойство очевидно без иллюстрации.
5. Сочетательное свойство умножения . К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.
6. Первое распределительное свойство . Это свойство достаточно очевидно.
7. Второе распределительное свойство . Это свойство справедливо в силу подобия треугольников, изображенных ниже.
8. Нейтральным числом по умножению является единица, то есть, . При умножении вектора на единицу с ним не производится никаких геометрических преобразований.

Рассмотренные свойства дают нам возможность преобразовывать векторные выражения.

Свойства коммутативности и ассоциативности операции сложения векторов позволяют складывать векторы в произвольном порядке.

Операции вычитания векторов как таковой нет, так как разность векторов и есть сумма векторов и .

Учитывая рассмотренные свойства операций над векторами, мы можем в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования так же как и в числовых выражениях.

Разберем на примере.

Пример.

Упростите выражение, содержащее векторы .

Решение.

Если воспользоваться вторым распределительным свойством операции умножения вектора на число, то получим .

В силу сочетательного свойства умножения имеем .

Свойство коммутативности операции сложения векторов позволяет поменять местами второе и третье слагаемые , а по первому распределительному свойству имеем .

А теперь запишем кратко: .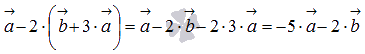

Ответ:

.

Список литературы.

• Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.

Некогда разбираться?