Формулы тригонометрии — коротко о главном
Основные формулы:
| Название формулы | Формула |
|---|---|
| Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!) | \( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\) |
| Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса) | \( \displaystyle tg\ \alpha =\frac{sin\ \alpha }{cos\ \alpha }\) |
| Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса) | \( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }=\frac{1}{tg\ \alpha }\) |
| Синус суммы и разности: | \( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \) |
| Косинус суммы и разности: | \( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \) |
| Тангенс суммы и разности: | \( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\) |
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
- \( \displaystyle si{{n}^{2}}\alpha =\frac{1-cos2\alpha }{2}\)
- \( \displaystyle co{{s}^{2}}\alpha =\frac{1+cos2\alpha }{2}\)
- \( \displaystyle si{{n}^{3}}\alpha =\frac{3sin\alpha -sin3\alpha }{4}\)
- \( \displaystyle co{{s}^{3}}a=\frac{3cosa+cos3a}{4}\)
- \( \displaystyle t{{g}^{2}}\alpha =\frac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \frac{\pi }{2}+\pi n,n\in Z\)
Формулы преобразования функций:
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
- \( \displaystyle sin\alpha \pm sin\beta =2sin\frac{\alpha \pm \beta }{2}cos\frac{\alpha \mp \beta }{2}\)
- \( \displaystyle cos\alpha +cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}\)
- \( \displaystyle cos\alpha -cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}\)
- \( \displaystyle tg\alpha \pm tg\beta =\frac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta }\)
- \( \displaystyle ctg\alpha \pm ctg\beta =\frac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta }\)
Формулы преобразования произведений функций:
- \( \displaystyle sin\alpha sin\beta =\frac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2}\)
- \( \displaystyle sin\alpha cos\beta =\frac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2}\)
- \( \displaystyle cos\alpha cos\beta =\frac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2}\)
Таблица значений тригонометрических функций:
Формулы общего вида
| (1) | Формула понижения nй четной степени синуса | |
| (2) | Формула понижения nй четной степени косинуса | |
| (3) | Формула понижения nй нечетной степени синуса | |
| (4) | Формула понижения nй нечетной степени косинуса |
— версия для печати
ОпределенияСинус угла α (обозн. sin(α)) — отношение противолежащего от угла α катета к гипотенузе.Косинус угла α (обозн. cos(α)) — отношение прилежащего к углу α катета к гипотенузе.Тангенс угла α (обозн. tg(α)) — отношение противолежащего к углу α катета к прилежащему. Эквивалентное определение — отношение синуса угла α к косинусу того же угла — sin(α)/cos(α).Котангенс угла α (обозн. ctg(α)) — отношение прилежащего к углу α катета к противолежащему. Эквивалентное определение — отношение косинуса угла α к синусу того же угла — cos(α)/sin(α).Другие тригонометрические функции: секанс — sec(α) = 1/cos(α);косеканс — cosec(α) = 1/sin(α).ПримечаниеМы специально не пишем знак * (умножить), — там, где две функции записаны подряд, без пробела, он подразумевается.ПодсказкаДля вывода формул косинуса, синуса, тангенса или котангенса кратных (4+) углов, достаточно расписать их по формулам соотв. косинуса, синуса, тангенса или котангенса суммы, либо сводить к предыдущим случаям, сводя до формул тройных и двойных углов.ДополнениеТаблица производных
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Употребление в устной речи
Запись
a
n
{\displaystyle a^{n}}
обычно читается как «a
в
n
{\displaystyle n}
-ой степени» или «a
в степени n
». Например,
10
4
{\displaystyle 10^{4}}
читается как «десять в четвёртой степени»,
10
3
/
2
{\displaystyle 10^{3/2}}
читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например,
10
2
{\displaystyle 10^{2}}
читается как «десять в квадрате»,
10
3
{\displaystyle 10^{3}}
читается как «десять в кубе». Такая терминология возникла из древнегреческой математики . Древние греки формулировали алгебраические конструкции на языке геометрической алгебры (англ.)
русск.
. В частности, вместо употребления слова «умножение» они говорили о площади
a
3
{\displaystyle a^{3}}
— это «a
умноженное само на себя три
раза» , имея в виду, что берётся три множителя
a
{\displaystyle a}
. Это не совсем точно, и может привести к двусмысленности, так как количество операций умножения будет на одну меньше:
a
3
=
a
⋅
a
⋅
a
{\displaystyle a^{3}=a\cdot a\cdot a}
(три множителя, но две операции умножения). Часто когда говорят, « изображалось как и
x
I
V
{\displaystyle x^{IV}}
соответственно . Начиная с Декарта , степень обозначали «двухэтажной» записью вида
a
b
{\displaystyle a^{b}}
.
С появлением компьютеров и компьютерных программ возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень в «двухэтажном» виде. В связи с этим изобрели особые значки для обозначения операции возведения в степень. Первым таким значком были две звёздочки
.
Некоторые знаки возведения в степень в языках программирования и компьютерных системах.
Основные тригонометрические тождества формул приведения
Формулы помогают, преобразовать основные тождества и перейти к вычислению углов в пределах 90 градусов. Это очень удобно, не только в алгебре, но и во всей математике.
Существует два основных способа, использования формул приведения:
- Если угол можно записать как (π/2 ±α) или (3*π/2 ±α), то название функции меняется с косинуса на определение синус, тангенс, в свою очередь на котангенс, либо наоборот. Если же угол можно представить в виде (π±α) или (2*π±α), то название функции не меняется.
- Обозначение приведенного уравнения не изменяется. Если изначально функция была со знаком «+», тогда и приведенная функция будет со знаком «+», с отрицательным знаком тоже самое.
Формулы приведения, примеры:
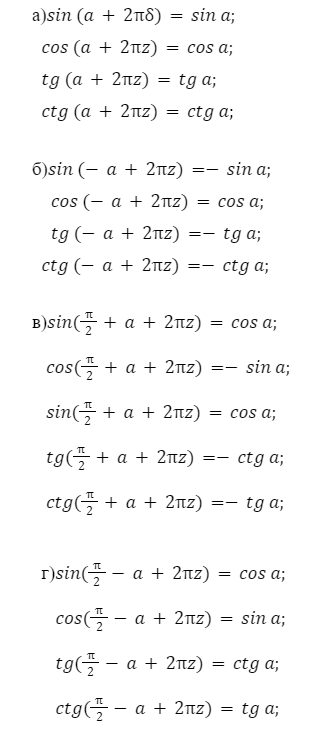
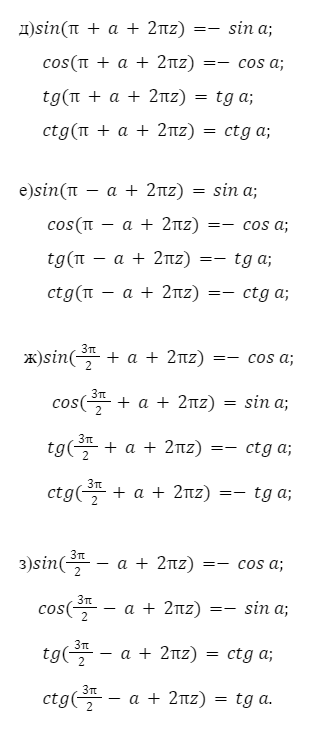
При расчетах очень часто возникают трудности при вычислении больших значений степеней. Для этого в тригонометрии, существует такое понятие как понижение значения степени.
Тождества понижения степени, помогают справиться с этой непростой задачей. Они выражают степень sin и cos через sin и cos первой степени, но определенного кратного угла. Поэтому, тригонометрические уравнения снижают степень первоначальных функций с определенной до первой степени, но при этом повышают кратность угла от до n.
Тригонометрические формулы для косинуса и синуса понижения степени, записываются в следующем виде:
После преобразования основных формул понижения получаем их общий вид. Рассмотрим на примерах ниже.
Для четных значений уравнения:

Для нечетных значений уравнения:
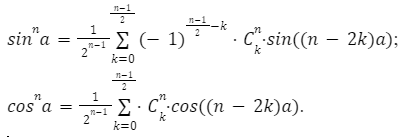
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | ||
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
|
02=0 12=1 22=4 32=9 42=16 52=25 62=36 72=49 82=64 92=81 |
102=100 112=121 122=144 132=169 142=196 152=225 162=256 172=289 182=324 192=361 |
202=400 212=441 222=484 232=529 242=576 252=625 262=676 272=729 282=784 292=841 |
302=900 312=961 322=1024 332=1089 342=1156 352=1225 362=1296 372=1369 382=1444 392=1521 |
402=1600 412=1681 422=1764 432=1849 442=1936 452=2025 462=2116 472=2209 482=2304 492=2401 |
|
502=2500 512=2601 522=2704 532=2809 542=2916 552=3025 562=3136 572=3249 582=3364 592=3481 |
602=3600 612=3721 622=3844 632=3969 642=4096 652=4225 662=4356 672=4489 682=4624 692=4761 |
702=4900 712=5041 722=5184 732=5329 742=5476 752=5625 762=5776 772=5929 782=6084 792=6241 |
802=6400 812=6561 822=6724 832=6889 842=7056 852=7225 862=7396 872=7569 882=7744 892=7921 |
902=8100 912=8281 922=8464 932=8649 942=8836 952=9025 962=9216 972=9409 982=9604 992=9801 |
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
= 36
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».
Скачать таблицу квадратов
- Нажмите на картинку чтобы посмотреть в увеличенном виде.
- Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.
Выражение одних тригонометрических функций через другие
`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами
. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Синусоидальная функция — исчисление
Эта функция, обозначаемая
Для краткости мы пишем
Ключевые данные
| пункт | |
|---|---|
| Домен по умолчанию | все действительные числа, то есть все |
| диапазон | , т.е. абсолютное максимальное значение: 1, абсолютное минимальное значение: 0 |
| период | , то есть |
| локальное максимальное значение и очки достижения | Все локальные максимальные значения равны 1 и достигаются при нечетных целых числах, кратных . |
| местное минимальное значение и очки достижения | Все локальные минимальные значения равны 0 и достигаются при целых числах, кратных . |
| точек перегиба (обе координаты) | нечетных кратных , со значением 1/2 в каждой точке. |
| производных | , то есть функция синусоидального угла. |
| вторая производная | |
| производная | раз выражение, которое составляет или из , в зависимости от остатка мод |
| антипроизводных | |
| среднее значение за период | 1/2 |
| выражение в виде синусоидальной функции плюс постоянная функция | |
| важных симметрий | (следует из составной части четной функции с нечетной функцией четного, квадратная функция четная, а синус-функция нечетная) в более общем случае зеркально симметрично относительно любой вертикальной линии формы , целое число. Кроме того, половина поворота симметрии вокруг всех точек формы . |
| описание интервала на основе увеличения / уменьшения и вогнутого вверх / вниз | Для каждого целого числа интервал от до подразделяется на четыре части: : увеличивается и вогнут до : увеличивается и вогнут : уменьшается и вогнут, : уменьшается и вогнут до |
| и серия Тейлор | Степенной ряд около 0 (что, следовательно, также ряд Тейлора) равен 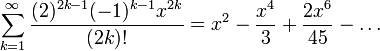 Это глобально сходящийся степенной ряд. Это глобально сходящийся степенной ряд. |
У нас есть следующие важные личности, связанные с
График
Вот график на интервале
![]()
Вот крупным планом график между
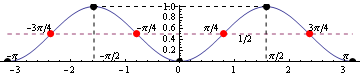
Красные пунктирные точки указывают точки перегиба, а черные пунктирные точки указывают локальные экстремальные значения.
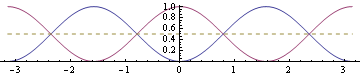
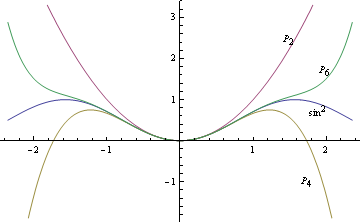
Вот изображение, показывающее функцию (синяя) и функцию квадрата косинуса (фиолетовая) с пунктирной линией
Дифференциация
Первая производная
У нас есть:
Мы можем сделать это двумя способами.
Используя цепное правило для дифференциации, мы имеем:
![]()
По формуле синусоидального угла это то же самое, что и
В качестве альтернативы, используя формулу косинуса двойного угла, мы переписываем:
В отличии мы получаем:
![]()
Снова дифференцируя производную, получаем:
![]()
Заполните это позже
точек и интервалов интереса
Рассмотрим
Это равно нулю точно в точках
Функция
Вторая производная
точек перегиба
Из определения интервалов, когда
- В точках с функция переходит от вогнутой вверх (слева) к вогнутой вниз (справа).
- В точках с функция переходит от вогнутой вниз (слева) к вогнутой вверх (справа).
Интеграция
Первый антидериватив
Теперь мы можем сделать интеграцию:
![]()
Чтобы интегрировать
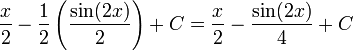
Использование интеграции по частям
Мы переписываем
![]()
Теперь мы переписываем
![]()
Если установить
Переставляя, получаем:
Это дает:
Итак, общее антидеривативное выражение:
Используя формулу двойного угла синуса
На рисунке ниже мы изображаем
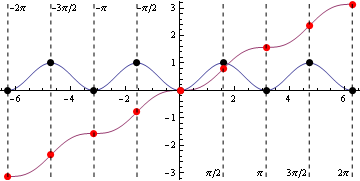
Черные точки соответствуют локальным крайним значениям для
Часть
линейная
Таким образом, имеем:
, где
Среднее значение для
На основе интегрирования
![]()
Таким образом, мы видим, что среднее значение этой функции также составляет
Антидифференцировать
Силовая серия и серия Тейлор
Вычисление степенных рядов
Мы можем использовать личность:
вместе с степенным рядом для функции косинуса, чтобы найти степенной ряд для
Степенной ряд для функции косинуса сходится к функции везде и имеет вид:
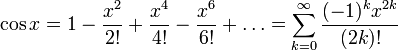
Силовая серия для
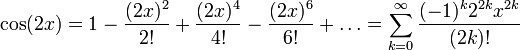
Силовая серия для
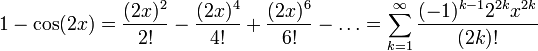
Разделив на 2, мы получим степенной ряд за
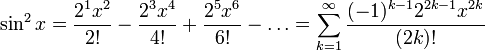
Вот еще одна формулировка, в которой первые несколько терминов написаны более явно:
Обратите внимание, что, поскольку
Предельные вычисления
Ноль порядка
Из степенных рядов получаем следующий предел:
Таким образом, порядок нуля
Этот предел может быть рассчитан многими способами:
У нас есть предел:
Этот предел может быть рассчитан многими способами:
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М
ы увидим, что она — основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как «работает» окружность — а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность
Тригонометрическая окружность — это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта «б» из задачи №13 профильного ЕГЭ.
Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте «б» необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.
Вообще-то решать пункт “б” можно двумя способами: — отметить корни уравнения на единичной окружности (способ разобранный в этом видео); — через двойное неравенство.
И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.
И еще один плюс второго способа — его проще оформить, так, чтобы к вам не придрались на ЕГЭ.
Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом
Основные формулы приведения в тригонометрии
Формулы приведения позволяют перейти от работы с произвольными и сколь угодно большими углами к работе с углами от 0 до 90 градусов, то есть преобразовать их.
Литые формулы
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctgα+ -ctgαsinπ2 +α +2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα=tπ2-α, cosπ2-α 2πz=ctgα, ctgπ2 -α +2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπz-α α+2πz=-cosαtgπ-α+2πz=- tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3πα2+α+2πz,=cc =-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=- sinαtg3π2- α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Комплексная степень
Сначала покажем, как вычисляется экспонента
e
z
{\displaystyle e^{z}}
, где e
— число Эйлера , z
— произвольное комплексное число ,
z
=
x
+
y
i
{\displaystyle z=x+yi}
.
e
z
=
e
x
e
y
i
=
e
x
(cos
y
+
i
sin
y)
=
e
x
cos
y
+
i
e
x
sin
y
.
{\displaystyle e^{z}=e^{x}e^{yi}=e^{x}(\cos y+i\sin y)=e^{x}\cos y+ie^{x}\sin y.}
Теперь рассмотрим общий случай , где
a
,
b
{\displaystyle a,b}
оба являются комплексными числами. Проще всего это сделать, представив
a
{\displaystyle a}
в экспоненциальной форме и используя тождество
a
b
=
e
b
Ln
(a)
{\displaystyle a^{b}=e^{b\ \operatorname {Ln} (a)}}
, где
Ln
{\displaystyle \operatorname {Ln} }
— комплексный логарифм :
a
b
=
(r
e
θ
i)
b
=
(e
Ln
(r)
+
θ
i)
b
=
e
(Ln
(r)
+
θ
i)
b
.
{\displaystyle a^{b}=(re^{{\theta }i})^{b}=(e^{\operatorname {Ln} (r)+{\theta }i})^{b}=e^{(\operatorname {Ln} (r)+{\theta }i)b}.}
Следует иметь в виду, что комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно.
Формулы понижения степени, их доказательство
Ниже приводится таблица формул понижения степенисо 2 по 4 для sin и cos угла. После ознакомления с ними зададим общую формулу для всех степеней.
sin2α=1-cos 2α2cos2α=1+cos 2α2sin3=3·sin α-sin 3α4sin4=3-4·cos 2α+cos 4α8cos4 α=3+4·cos 2α+cos 4α8
Данные формулы предназначены для понижения степени.
Существует формулы двойного угла у косинуса и синуса, из которых и следуют формулы понижения степени cos2α=1-2·sin2α и cos2α=2·cos2α-1. Равенства разрешаются относительно квадрата синуса и косинуса, которые предоставляются как sin2α=1-cos2α2 и cos2α=1+cos2α2.
Формулы понижения степеней тригонометрических функций перекликаются с формулами синуса и косинуса половинного угла.
Имеет место применение формулы тройного угла sin3α=3·sinα-4·sin3αи cos3α=-3·cosα+4·cos3α.
Если решать равенство относительно синуса и косинуса в кубе, получим формулы понижения степеней для синуса и косинуса:
sin3α=3-4·cos2α+cos4α8 и cos3α=3·cosα+cos3α4.
Формулы четвертой степени тригонометрических функций выглядят так: sin4α=3-4·cos2α+cos4α8 и cos4α=3+4·cos2α+cos4α8.
Чтобы понизить степени эти выражений, можно действовать в 2 этапа, то есть дважды понижать, тогда это выглядит таким образом:
sin4α =(sin2α)2=(1-cos2α2)2=1-2·cos2α+cos22α4==1-2·cos2α+1+cos4α24=3-4·cos2α+cos4α8;cos4α=(cos2α)2=(1+cos2α2)2=1+2·cos2α+cos22α4===1+2·cos2α+1+cos4α24=3+4·cos2α+cos4α8
Методом подстановки мы упростили сложное выражение. Для того, чтобы записать общий вид формул понижения степени разделим их на с наличием четных и нечетных показателей. Четные показатели, где n=2, 4, 6…, выражение имеет вид sinnα=Cn2n2n+12n-1·∑(-1)n2-kk=0n2-1·Ckn·cos((n-2·k)α) и cosnα=Cn2n2n+12n-1∑(-1)n2-kk=0n2-1·Ckn·cos((n-2·k)α).
Нечетные показатели, где n=3, 5, 7…, выражение имеет вид
sinnα=12n-1·∑(-1)n-12-kk=0n-12·Ckn·cos((n-2·k)α) и cosnα=12n-1∑(-1)n-12-kk=0n-12·Ckn·cos((n-2·k)α).
Cpq=p!q!·(p-q)! – это число сочетаний из p элементов по q.
Формулы понижения степени общего вида используются на любого выражения с высокой степенью для его упрощения. Рассмотрим пример для понижения кубического синуса. Третья степень нечетная, значит воспользуемся формулой sinnα=12n-1·∑(-1)n-22-kk=0n-12-k·Ckn·sin((n-2·k)α) где значение n присвоим 3. Подставляя n=3 в выражение, получим
sin3α=123-1·∑(-1)3-12-kk=03-12-k·Ck3·sin((3-2·k)α)==14·∑(-1)1-kk=01·Ck3·sin((3-2·k)α)==14·((-1)1-0·C03·sin((3-2·0)α) +(1)1-1·C13·sin((3-2·1)α))==14·((-1)1·3!0!·3!·sin3α+(-1)0·3!1!·(3-1)!·sinα)==14·(-sin3α+3·sinα)=3·sinα-sin3α4
Свойства степени — 2 части
Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени.
Степень
Число
c
{\displaystyle c}
называется n
-й степенью числа
a
{\displaystyle a}
, если
c
=
a
⋅
a
⋅
.
.
.
⋅
a
⏟
n
{\displaystyle c=\underbrace {a\cdot a\cdot …\cdot a} _{n}}
Свойства:
-
(a
b)
n
=
a
n
b
n
{\displaystyle \left(ab\right)^{n}=a^{n}b^{n}} -
(a
b)
n
=
a
n
b
n
{\displaystyle \left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}} -
a
n
a
m
=
a
n
+
m
{\displaystyle a^{n}a^{m}=a^{n+m}} -
a
n
a
m
=
a
n
−
m
{\displaystyle \left.{a^{n} \over {a^{m}}}\right.=a^{n-m}} -
(a
n)
m
=
a
n
m
{\displaystyle \left(a^{n}\right)^{m}=a^{nm}} - запись не обладает свойством ассоциативности (сочетательности), то есть в общем случае левая ассоциативность не равна правой ассоциативности
(a
n)
m
≠
a
(n
m)
{\displaystyle (a^{n})^{m}\neq a^{\left({n^{m}}\right)}}
, результат будет зависеть от последовательности действий, например,
(2
2)
3
=
4
3
=
64
{\displaystyle (2^{2})^{3}=4^{3}=64}
, а
2
(2
3)
=
2
8
=
256
{\displaystyle 2^{\left({2^{3}}\right)}=2^{8}=256}
. Принято считать запись
a
n
m
{\displaystyle a^{n^{m}}}
равнозначной
a
(n
m)
{\displaystyle a^{\left({n^{m}}\right)}}
, а вместо
(a
n)
m
{\displaystyle (a^{n})^{m}}
можно писать просто
a
n
m
{\displaystyle a^{nm}}
, пользуясь предыдущим свойством. Впрочем некоторые языки программирования не придерживаются этого соглашения (см. ); - возведение в степень не обладает свойством коммутативности (переместительности) : вообще говоря,
a
b
≠
b
a
{\displaystyle a^{b}\neq b^{a}}
, например,
2
5
=
32
{\displaystyle 2^{5}=32}
, но
5
2
=
25
{\displaystyle 5^{2}=25}
.
Таблица степеней
Пример: 2 3 =8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




















![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://rwvt.ru/wp-content/uploads/a/d/4/ad484f5d1956e94fb07202f1996c5d5c.jpeg)









