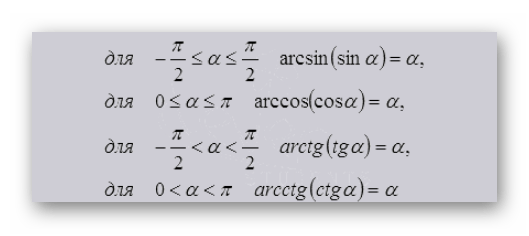Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 9. Тригонометрическая окружность, табличные значения

На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М

ы увидим, что она — основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.

Мы поймем, как «работает» окружность — а значит, поймём тригонометрию в целом.

ЕГЭ 13б. Тригонометрическая окружность

Тригонометрическая окружность — это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта «б» из задачи №13 профильного ЕГЭ.

Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте «б» необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.

Вообще-то решать пункт “б” можно двумя способами: — отметить корни уравнения на единичной окружности (способ разобранный в этом видео); — через двойное неравенство.

И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.

И еще один плюс второго способа — его проще оформить, так, чтобы к вам не придрались на ЕГЭ.

Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом

Основные соотношения между элементами косоугольных треугольников

Обозначения:

$a$, $b$, $c$ — стороны треугольника;

$A$, $B$, $C$ — противолежащие перечисленным сторонам углы;

$p=\frac{a+b+c}{2} $ — полупериметр;

$S$ — площадь;

$R$ — радиус описанной окружности;

$r$ — радиус вписанной окружности.

Основные соотношения:

1) $\frac{a}{\sin A} =\frac{b}{\sin B} =\frac{c}{\sin C} =2\cdot R$ — теорема синусов;

2) $a^{2} =b^{2} +c^{2} -2\cdot b\cdot c\cdot \cos A$ — теорема косинусов;

3) $\frac{a+b}{a-b} =\frac{tg\frac{A+B}{2} }{tg\frac{A-B}{2} } $ — теорема тангенсов;

4) $S=\frac{1}{2} \cdot a\cdot b\cdot \sin C=\sqrt{p\cdot \left(p-a\right)\cdot \left(p-b\right)\cdot \left(p-c\right)} =r\cdot p=\frac{a\cdot b\cdot c}{4\cdot R} $ — формулы площади.

Решение 3-х более сложных уравнений

Уравнение 12. Най­ди­те корни урав­не­ния: \( \displaystyle cos\frac{8\pi x}{6}=\frac{\sqrt{3}}{2}\). В от­ве­те за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!

Если бы мы решали уравнение вида:

\( \displaystyle cost=\frac{\sqrt{3}}{2}\)То мы бы записали вот такой ответ:

\( \displaystyle t=\pm arccos\frac{\sqrt{3}}{2}+2\pi n,~n\in Z\)Или (так как \( \displaystyle arccos\frac{\sqrt{3}}{2}=\frac{\pi }{6}\))

\( \displaystyle t=\pm \frac{\pi }{6}+2\pi n,~n\in Z\)Но теперь в роли \( \displaystyle t\) у нас выступаем вот такое выражение: \( \displaystyle t=\frac{8\pi x}{6}\)

Тогда можно записать:

\( \displaystyle \frac{8\pi x}{6}=\pm \frac{\pi }{6}+2\pi n\)Наша с тобою цель – сделать так, чтобы слева стоял просто \( \displaystyle x\), без всяких «примесей»!

Давай постепенно от них избавляться!

Вначале уберём знаменатель при \( \displaystyle x\): для этого домножим наше равенство на \( \displaystyle 6\):

\( \displaystyle \frac{6\cdot 8\pi x}{6}=6\cdot \left( \pm \frac{\pi }{6}+2\pi n \right)\)\( \displaystyle 8\pi x=\pm \frac{6\pi }{6}+12\pi n\)\( \displaystyle 8\pi x=\pm \pi +12\pi n\)Теперь избавимся от \( \displaystyle \pi \), разделив на него обе части:

\( \displaystyle 8x=\pm 1+12n\)Теперь избавимся от восьмёрки:\( \displaystyle \frac{8x}{8}=\pm \frac{1}{8}+\frac{12n}{8}\)\( \displaystyle x=\pm \frac{1}{8}+\frac{3n}{2}\)Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)\( \displaystyle x=\frac{1}{8}+\frac{3n}{2}\)или\( \displaystyle x=-\frac{1}{8}+\frac{3n}{2}\)Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать \( \displaystyle n\).

Формулы тригонометрии — коротко о главном

Основные формулы:

Название формулы	Формула
Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!)	\( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\)
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)	\( \displaystyle tg\ \alpha =\frac{sin\ \alpha }{cos\ \alpha }\)
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)	\( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }=\frac{1}{tg\ \alpha }\)
Синус суммы и разности:	\( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \)
Косинус суммы и разности:	\( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \)
Тангенс суммы и разности:	\( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\)

Формулы понижения степени:

Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.

• \( \displaystyle si{{n}^{2}}\alpha =\frac{1-cos2\alpha }{2}\)
• \( \displaystyle co{{s}^{2}}\alpha =\frac{1+cos2\alpha }{2}\)
• \( \displaystyle si{{n}^{3}}\alpha =\frac{3sin\alpha -sin3\alpha }{4}\)
• \( \displaystyle co{{s}^{3}}a=\frac{3cosa+cos3a}{4}\)
• \( \displaystyle t{{g}^{2}}\alpha =\frac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \frac{\pi }{2}+\pi n,n\in Z\)

Формулы преобразования функций:

Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.

• \( \displaystyle sin\alpha \pm sin\beta =2sin\frac{\alpha \pm \beta }{2}cos\frac{\alpha \mp \beta }{2}\)
• \( \displaystyle cos\alpha +cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}\)
• \( \displaystyle cos\alpha -cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}\)
• \( \displaystyle tg\alpha \pm tg\beta =\frac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta }\)
• \( \displaystyle ctg\alpha \pm ctg\beta =\frac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta }\)

Формулы преобразования произведений функций:

• \( \displaystyle sin\alpha sin\beta =\frac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2}\)
• \( \displaystyle sin\alpha cos\beta =\frac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2}\)
• \( \displaystyle cos\alpha cos\beta =\frac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2}\)

Таблица значений тригонометрических функций:

Решение 3-х примеров для самостоятельной работы

• Ре­ши­те урав­не­ние \( \displaystyle sin\frac{\pi x}{3}=0,5\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.
• Ре­ши­те урав­не­ние \( \displaystyle tg\frac{\pi \left( {x}-6 \right)}{6}=\frac{1}{\sqrt{3}}\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.
• Ре­ши­те урав­не­ние \( \displaystyle sin\frac{\pi \left( 2{x}-3 \right)}{6}=-0,5\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

Готов? Проверяем. Я не буду подробно описывать весь алгоритм решения, мне кажется, ему и так уделено достаточно внимания выше.

Алгоритм вычисления арксинусов и других «арок»

• Смотрим на то, что стоит под «аркой» – какое там число
• Смотрим, какая у нас «арка» – для синуса ли, или для косинуса, тангенса или котангенса
• Смотрим, чему равен угол (1 четверти), для которого синус, косинус, тангенс, котангенс равен числу, стоящему под аркой
• Записываем ответ

Вот простой пример вычисления аркосинуса:

Решение:

• Под аркой число \( \displaystyle \frac{\sqrt{3}}{2}\)
• Арка для функции – косинус!
• Косинус какого угла равен \( \displaystyle \frac{\sqrt{3}}{2}\)? Угла \( \displaystyle \frac{\pi }{6}\) (или \( \displaystyle 30\) градусов!)
• Тогда \( \displaystyle \arccos \left( \frac{\sqrt{3}}{2} \right)=\frac{\pi }{6}\)

Сам посчитай:

• \( \displaystyle \ arctg\left( \frac{1}{\sqrt{3}} \right)\)
• \( \displaystyle \arcsin \left( \frac{\sqrt{3}}{2} \right)\)

Ответы:

Пример задачи на использование формул тригонометрии

sin5x·cos3x − sin8x·cos6x = 0.

Имеем две разные функции sin() и cos() и четыре! разных аргумента 5x, 3x, 8x и 6x. Без предварительных преобразований свести к простейшим типам тригонометрических уравнений не получится. Поэтому сначала пробуем заменить произведения на суммы или разности функций. Делаем это так же, как в примере выше (см. раздел ).

sin(5x + 3x) + sin(5x − 3x) = 2·sin5x·cos3x
sin8x + sin2x = 2·sin5x·cos3x

sin(8x + 6x) + sin(8x − 6x) = 2·sin8x·cos6x
sin14x + sin2x = 2·sin8x·cos6x

(sin8x + sin2x)/2 − (sin14x + sin2x )/2 = 0.

xxxxxx

Уравнение значительно упростилось, но решать его так sin8x = sin14x, следовательно 8x = 14x + T, где Т — период, неверно, так как мы не знаем значения этого периода. Поэтому воспользуемся тем, что в правой части равенства стоит 0, с которым легко сравнивать множители в любом выражении.
Чтобы разложить sin8x − sin14x на множители, нужно перейти от разности к произведению. Для этого можно воспользоваться формулой разности синусов, или снова формулой суммы синусов и нечётностью функции синус (см. пример в разделе ).

sin8x − sin14x = sin8x + sin(−14x) = 2·sin 8x + (−14x)__________   2·cos 8x − (−14x)__________   2  = sin(−3x)·cos11x = −sin3x·cos11x.

Итак, уравнение sin8x − sin14x = 0 равносильно уравнению sin3x·cos11x = 0, которое, в свою очередь, равносильно совокупности двух простейших уравнений sin3x = 0 и cos11x = 0. Решая последние, получаем две серии ответовx₁ = πn/3, nϵZx₂ = π/22 + πk/11, kϵZ

Если Вы обнаружили ошибку или опечатку в тексте, сообщите о ней, пожалуйста, на электронный адрес [email protected]. Буду весьма признательна.

 Перейти  на главную страницу сайта.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы?   пожелания?  замечания? Обращайтесь —
  [email protected]

Внимание, mathematichka. Прямое копирование материалов на других сайтах запрещено

Ставьте ссылки.

Формулы суммы и разности

Аналогичным способом, получим формулу суммы арксинусов.

Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin
x
,
Y = arcsin
y
.
Формула применима при.
Далее замечаем, что, поскольку arcsin(-
x) = — arcsin
x,
arcsin(-
y) = — arcsin
y,
то при разных знаках у x
и y
,
X
и Y
также разного знака и поэтому неравенства выполняются. Условие различных знаков у x
и y
можно написать одним неравенством: .
То есть при формула справедлива.

Теперь рассмотрим случай x > 0

и y > 0

,
или X > 0

и Y > 0

.
Тогда условие применимости формулы заключается в выполнении неравенства: .
Поскольку косинус монотонно убывает при значениях аргумента в интервале от ,
до π
,
то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:;
;
;
.
Поскольку и ;
то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:;
.
Подставляем sin
X = sin arcsin
x = x
:
;
;
;
.

Итак, полученная формула справедлива при или .

Теперь рассмотрим случай x > 0, y > 0
и x 2 + y 2 > 1

.
Здесь аргумент синуса принимает значения: .
Его нужно привести к интервалу области значения арксинуса :

Итак, при и.

Заменив x
и y
на — x
и — y
,
имеем при и.
Выполняем преобразования: при и.
Или при и.

Итак, мы получили следующие выражения для суммы арксинусов: при или ; при и ; при и .

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.

Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.

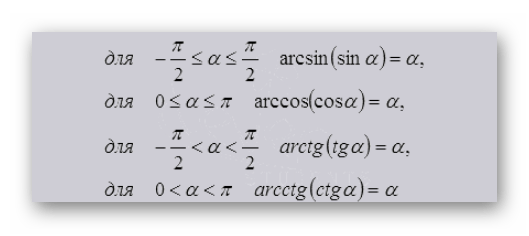
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сопоставить графики sin
и arcsin
, у двух тригонометрических функций можно найти общие закономерности.

Формулы половинного угла (двойного аргумента)

$$\sin^2\left(\frac{\alpha}{2}\right)=\frac{1-\cos(\alpha)}{2};$$
$$\cos^2\left(\frac{\alpha}{2}\right)=\frac{1+\cos(\alpha)}{2};$$
$$tg^2\left(\frac{\alpha}{2}\right)=\frac{1-\cos(\alpha)}{1+\cos(\alpha)};$$
$$ctg^2\left(\frac{\alpha}{2}\right)=\frac{1+\cos(\alpha)}{1-\cos(\alpha)};$$

Формулы половинного угла это по сути формулы обратные формулам двойного угла. Достаточно запомнить их элементарный вывод, тогда учить совсем необязательно. Здесь важный момент, что любой угол \(\alpha\) всегда можно представить в виде удвоенного угла \(\frac{\alpha}{2}\):
$$\alpha=2*\frac{\alpha}{2};$$

Выведем формулу синуса половинного угла, для этого нам понадобится формула косинуса двойного угла:
$$\cos(\alpha)=1-2*\sin^2\left(\frac{\alpha}{2}\right);$$
Выразим отсюда \(\sin(\frac{\alpha}{2})\):
$$\sin^2\left(\frac{\alpha}{2}\right)=\frac{1-\cos(\alpha)}{2};$$
Иногда эту формулу записывают без квадрата:
$$\sin\left(\frac{\alpha}{2}\right)=\pm\sqrt{\frac{1-\cos(\alpha)}{2}};$$
Плюс минус возникает при избавлении от квадрата.
Вывод косинуса половинного угла тоже получается из формулы косинуса двойного угла:
$$\cos(\alpha)=2*\cos^2\left(\frac{\alpha}{2}\right)-1;$$
$$\cos^2\left(\frac{\alpha}{2}\right)=\frac{\cos(\alpha)+1}{2};$$
$$\cos\left(\frac{\alpha}{2}\right)=\pm\sqrt{\frac{\cos(\alpha)+1}{2}};$$

Доказательство формул половинного угла для тангенса и котангенса следует из выше доказанных формул:
$$tg\left(\frac{\alpha}{2}\right)=\frac{\sin(\frac{\alpha}{2})}{\cos(\frac{\alpha}{2})}=\frac{\pm\sqrt{\frac{1-\cos(\alpha)}{2}}}{\pm\sqrt{\frac{\cos(\alpha)+1}{2}}}=\sqrt{\frac{\frac{1-\cos(\alpha)}{2}}{\frac{\cos(\alpha)+1}{2}}}=\frac{1-\cos(\alpha)}{1+\cos(\alpha)};$$
Точно так же для котангенса:
$$сtg\left(\frac{\alpha}{2}\right)=\frac{\cos(\frac{\alpha}{2})}{\sin(\frac{\alpha}{2})}=\frac{\pm\sqrt{\frac{\cos(\alpha)+1}{2}}}{\pm\sqrt{\frac{1-\cos(\alpha)}{2}}}=\sqrt{\frac{\frac{\cos(\alpha)+1}{2}}{\frac{1-\cos(\alpha)}{2}}}=\frac{1+\cos(\alpha)}{1-\cos(\alpha)};$$

Пример 9
При помощи формул половинного угла можно, например, посчитать \(\cos(15^o)\):

$$\cos^2\left(\frac{\alpha}{2}\right)=\frac{1+\cos(\alpha)}{2};$$
$$\cos^2(15^o)=\frac{1+\cos(30^o)}{2}=\frac{1+\frac{\sqrt{3}}{2}}{2}=\frac{2+\sqrt{3}}{4};$$
$$\cos(15^o)=\sqrt{\frac{2+\sqrt{3}}{4}}.$$

Кстати, формулы половинного угла справедливы не только в явном виде, когда аргумент правой части формулы \(\alpha\), а левой \(\frac{\alpha}{2}\). Но и в неявном, достаточно, чтобы аргумент правой части был больше аргумента левой в два раза:
$$\sin(5\alpha)=\pm\sqrt{\frac{1-\cos(10\alpha)}{2}};$$

Преобразование отрицательных углов тригонометрических функций (четность и нечетность)

Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.

Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

I группа. Основные тождества

sin2α + cos2α = 1;

tgα = ____sinαcosα ;     ctgα = ____cosαsinα ;

tgα·ctgα = 1;

1 + tg2α = _____   1cos2α;     1 + ctg2α = _____   1sin2α .

Эта группа содержит самые простые и самые востребованные формулы. Большинство учащихся их знает. Но если всё-таки есть трудности, то чтобы запомнить первые три формулы, мысленно представьте себе прямоугольный треугольник с гипотенузой равной единице. Тогда его катеты будут равны, соответственно, sinα по определению синуса (отношение противолежащего катета к гипотенузе) и cosα по определению косинуса (отношение прилежащего катета к гипотенузе).

Первая формула представляет собой теорему Пифагора для такого треугольника — сумма квадратов катетов равна квадрату гипотенузы (12 = 1), вторая и третья — это определения тангенса (отношение противолежащего катета к прилежащему) и котангенса (отношение прилежащего катета к противолежащему). Произведение тангенса на котангенс равно 1 потому, что котангенс, записанный в виде дроби (формула третья) есть перевернутый тангенс (формула вторая). Последнее соображение, кстати, позволяет исключить из числа формул, которые необходимо обязательно заучить, все последующие длинные формулы с котангенсом. Если в каком-либо сложном задании Вам встретится ctgα, просто замените его на дробь ___  1tgα и пользуйтесь формулами для тангенса.

Последние две формулы можно не запоминать досимвольно. Они встречаются реже. И если потребуются, то Вы всегда сможете вывести их на черновике заново. Для этого достаточно подставить вместо тангенса или контангенса их определения через дробь (формулы вторая и третья, соответственно) и привести выражение к общему знаменателю

Но важно помнить, что такие формулы, которые связывают квадраты тангенса и косинуса, и квадраты котангенса и синуса существуют. Иначе, Вы можете не догадаться, какие преобразования необходимы для решения той или иной конкретной задачи

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.

Формулы понижения степени

Для чего применяются

С их помощью можно приводить тригонометрические уравнения к уравнениям более низких степеней, вплоть до первой степени

Важно помнить, что при понижении степени аргумент увеличивается

Общий вид 

Для четных n:

\(\sin^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}{(-1)}^{{\textstyle\frac n2}-k}\;\times\;C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

\(\cos^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

Для нечетных n:

\(\sin^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum{(-1)}^{\frac{n-1}2-k}\;\times\;}}C_n^k\;\times\;\sin\left((n-2\times k)\times\alpha\right)\)

\(\cos^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum\;}}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)

\(C_p^q\;=\;\frac{p!}{q!(p-q)!}\)

Это означает число сочетаний из p элементов по q.

Противоположные числа

Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).

Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.

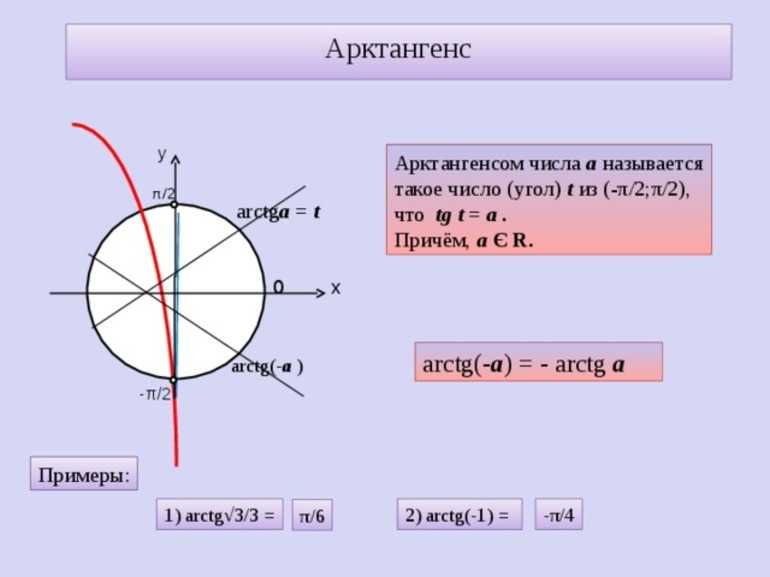
Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.

Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.

Используя свойства неравенств, перемножаются поочерёдно его части на -1, сменяются знаки. Решается неравенство из сумм частей и числа пи, при этом сохраняются знаки: −π+π≤−arccosa+π≤0+π. Получается двойное выражение вида 0≤π−arccos a≤π.

Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.

https://youtube.com/watch?v=4HDNSPmzG18