Таблица производных: доказательство формул

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

Решение уравнения cosx = a

Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:

По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь

Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:

Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:

Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:

Здесь мы использовали тот факт, косинус – четная функция, то есть

Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:

Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть

Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:

Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение

При n = 5 получим корень

При n = – 10 у нас получится решение

Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:

Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень

Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:

Объединить же обе серии можно одной записью:

Напомним, что мы решали ур-ние

и получили для него решение

Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид

где а – некоторое число, его решением будут все такие х, что

Для краткости запись «n– целое число» заменяют эквивалентной записью

«n ∈ Z»

Напомним, что буквой Z обозначают множество целых чисел.

Задание. Решите ур-ние

Решение. Вспомним, что

Задание. Решите ур-ние

Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:

Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.

Задание. Укажите три наименьших положительных корня ур-ния

Решение. Так как

то все решения образуют две серии:

Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.

Для первой серии:

Для второй серии:

Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):

Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4

Ответ: π/4, 7π/4 и 9π/4.

Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния

На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния

являются точки, в которых график пересекает ось Ох:

Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок .

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ2 + ОВ2 = ОА2

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin2α + соs2α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin2α + соs2α = 1

0,82 + соs2α = 1

0,64 + соs2α = 1

соs2α = 1 – 0,64

соs2α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin2α + соs2α = 1

0,282 + sin2α = 1

0,0784 + sin2α = 1

sin2α = 1 – 0,0784

sin2α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin2α + соs2α = 1

соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin2α + соs2α = 1

Далее поделим его на величину соs2α:

Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:

Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin2α + соs2α = 1

sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения

sin2α = 1 – соs2α

и

соs2α = 1 – sin2α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin2α + 9соs2α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin2α = 1 – соs2α:

4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =

= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs2α – 2.

Задание. Избавьтесь от синуса в выражении

sin4α – соs4α

Решение. Воспользуемся ф-лой :

sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =

= 1 – соs2α– соs2α = 1 – 2 соs2α

Ответ:1 – 2 соs2α.

Задание. Упростите дробь

Решение.

Ответ: ctg6α.

Формулы производных для тригонометрических функций

Преобразования синуса, косинуса, тангенса и котангенса при определении производной необходимо заучить наизусть.

Последние две формулы не являются ошибкой, дело в том, что существует разница между определением производной простого аргумента и  функции в том же качестве.

Рассмотрим сравнительную таблицу с формулами производных от синису, косинуса, тангенса и котангенса:

Также выведены формулы для производных арксинуса, арккосинуса, арктангенса и арккотангенса, хотя они применяются крайне редко:

Стоит отметить, что приведенных формул явно недостаточно для успешного решения типовых заданий ЕГЭ, что будет продемонстрированно при решении конкретного примера поиска производной тригонометрического выражения.

Задание: Необходимо найти производную функции и найти ее значение для π/4:

Решение:  Чтобы найти y’ необходимо вспомнить основные формулы преобразования исходной функции в производную, а именно:

Теперь следует приступить к поэтопному преобразованию исходной функции y, сначала применим формулу (1):

Согласно формуле (2) преобразуем числитель выражения:

Избавимся от производным числа 1 по правилу (3) и заменим sin x его производной (4):

Осталось посчитать значение производной для π/4:

Уравнения, сводящиеся к виду tgx=a

Ну вот, теперь самое время переходить ко второй порции уравнений, тем более, что я уже и так проболтался в чем состоит решение тригонометрических уравнений нового типа.

Но не лишним будет повторить, что уравнение вида

\( \displaystyle \text{acosx}+\text{bsinx}=0\text{ }\!\!~\!\!\text{ }\left( \text{a},\text{b}\ne 0 \right)\)Решается делением обеих частей на косинус:

\( \displaystyle \text{a}\frac{\text{cosx}}{\text{cosx}}+\text{b}\frac{\text{sinx}}{\text{cosx}}=0\)\( \displaystyle \text{a}+\text{btgx}=0\)\( \displaystyle \text{tgx}=-\frac{\text{a}}{\text{b}}\)Таким образом, решить уравнение вида

\( \displaystyle \text{acosx}+\text{bsinx}=0 \)все равно, что решить

Производная тригонометрических функций: синуса, косинуса, тангенса

Используя тригонометрические формулы выведем основное доказательство для производной данного вида функции.

Для производного синуса составим и запишем следующее выражение:

\

Применение формулы разности тригонометрической функции синус, позволит выполнить ряд последующих преобразований и действий.

\

Используя первый предел получаем формулу:

\

Следовательно, производной для функции sin x будет являться cos x.

Аналогичным образом происходит доказательство и другой функции косинус.

\

Для тригонометрической функции косинус, производной будет являться синус с отрицательным знаком.

Применяя общие правила дифференциации, можно вывести главные формулы для тангенса и котангенса.

\
\

Производная функции возведенной в степень.

Выполним доказательство основного уравнения производной функции.

Показатель степени возьмем равным p=1.2.3…

Используя основное определение производной выполним доказательство.

Составим выражение предела отношения приращения степенной степени.

\

Применяя формулу бинома Ньютона выполним упрощение выражения в числителе.

\

Следовательно:

\

Таким образом формула производной возведенной в степень является доказанной.

Когда показатель p — это любое действительное число, и не равно нулевому значению. Нужно использовать логарифмическую производную. Обязательно нужно различать понятие логарифмической функции и производной.

Нахождение значения аргумента

Например, найдем все значения аргумента, при которых значение функции

На единичной окружности найдем точки
ординаты которых равны 
Этим точкам соответствуют углы 
и
и таких углов бесконечно много. Однако, если рассмотреть промежуток  то на нем функция 
возрастает и принимает все значения от -1 до 1. Поэтому для любого числа
из промежутка 
существует единственное число  такое что
Так на промежутке
существует единственное значение аргумента, при котором значение функции равно  — это угол равный 
( рис.93)

Определение Арксинуса

Этот угол обозначают 
Так,  поскольку  и 

Вычислите:

Решение:

так как 

Пример №2

Найдите значение выражения:

Решение:

так как

(рис. 95, б).

Заметим, что 
( рис.95)  Так как углы, соответствующие точкам
и
где 
с ординатами 
и
отличаются только знаком, то
для любого числа 
(рис. 96).

Пусть 
тогда 
Так как точки
имеют противоположные ординаты, то 
Поскольку  то по определению арксинуса 
Так как  то для любого числа 
Воспользуемся полученным равенством и найдем значение выражения

Так как 

Отметим, что областью определения выражения 
является отрезок  Если 
то выражение не имеет смысла.

Например, выражения  не имеют смысла, так как 
Выражение не имеет смысла, так как 
Из определения арксинуса числа следует, что 
если 

Например, 

Рассмотрим промежуток  на котором функция 
возрастает и принимает все значения от до 1. Для любого числа  из промежутка 
существует единственное число  такое, что 

Определение Арккосинуса

Этот угол обозначают 

Например:  поскольку 
и 

Вычислите:

Решение:

Пример №4

Найдите значение выражения:

Решение:

так как 
( рис. 98.а)

( рис.98.б)

Заметим, что 
( см.98)

Пусть 
Так как точки 
имеют противоположные абсциссы, то 
Поскольку то по определению арккосинуса
Так как для любого числа (рис. 99).

Воспользуемся полученным равенством и найдем значение выражения

Так как 
Областью определения выражения  является отрезок 
Если  то выражение не имеет смысла.

Так, выражения
не имеют смысла, поскольку

Выражение 
не имеет смысла, так как 
Из определения арккосинуса числа следует, что
если  и 

Например, 

На промежутке монотонности функции существует единственный угол, тангенс которого равен некоторому данному числу 

Определение Арктангенса

Этот угол обозначают 
Так,  поскольку и 

Вычислите:

Решение:

так как 
и 

и 

Для любого числа 
верно равенство 
(рис. 101).

Пример №6

Найдите значение выражения

Решение:

Так как 
Из определения арктангенса числа следует, что 
при 

Например, 

На промежутке монотонности
функции 
существует единственный угол, котангенс которого равен некоторому данному числу 

Определение Арккотангенса

Этот угол обозначают 
Например, поскольку

Вычислите:

Решение:

так как

Для любого числа 
верно равенство 
(рис. 103).

Пример №8

Найдите значение выражения 

Решение:

Так как 

Из определения арккотангенса числа следует, что 
если
и 

Например, 

Примеры заданий и их решения

Верно ли, что:

Решение:

• Верно, так как
• верно, так как
• неверно, так как
• неверно, так как

Вычислите:

Решение:

Найдите значение выражения:

Решение:

Оцените значение выражения 

Решение:

По определению арктангенса числа 

Воспользуемся свойствами числовых неравенств и получим: 

Найдите область определения выражения:

Решение:

• По определению арксинуса числа
  это угол, синус которого равен 
•  По определению арккосинуса числа
  это угол, косинус которого равен 

Найдите значение выражения:

Решение:

Вычислите 

Решение:

Найдите значение выражения 

Решение:

Воспользуемся формулой
при 
Поскольку 
то эту формулу сразу применить нельзя.

Так как 

Понятие производной

Итак, рассмотрим некую произвольную кривую, которая описывается абстрактной функцией y = f(x).

Представим что график — это карта туристического маршрута. Приращение ∆x (дельта икс) на рисунке — это определенный промежуток пути, а ∆y – это изменение высоты тропы над уровнем моря.
Тогда получается, что отношение ∆x/∆y будет характеризовать сложно маршрута на каждом отрезке пути. Узнав это значение можно с уверенностью сказать крутой ли подъем/спуск, понадобится ли альпинистское снаряжение и нужна ли туристам определенная физическая подготовка. Но показатель этот будет справедлив только для одного маленького промежутка ∆x.

Если организатор похода возьмет значения для начальной и конечной точек тропы, то есть ∆x – будет равен длине маршрута, то не сможет получить объективные данные о степени сложности путешествия.  Следовательно, необходимо построить еще один график, который будет характеризовать скорость и «качество» изменений пути, другими словами определять отношение ∆x/∆y для каждого «метра» маршрута.

Этот график и будет являться наглядной производной для конкретной тропы и объективно опишет ее изменения на каждом интересующем интервале. Убедиться в этом очень просто, значение  ∆x/∆y – есть не что иное, как дифференциал, взятый для конкретного значения x и y. Применим же дифференцирование не определенным координатам, а к функции в целом:

Функция arctg[]

Файл:Arctg.png

График функции y=arctgx{\displaystyle y=\operatorname {arctg} \,x}.

Арктангенсом числа m называется такой угол x, для каторого tgx=m,−π2<x<π2.{\displaystyle \operatorname {tg} \,x=m,\qquad -{\frac {\pi }{2}}<x<{\frac {\pi }{2}}.}

Функций y=arctg⁡x{\displaystyle y=\operatorname {arctg} x} непрерывна и ограничена на всей своей числовой прямой. Функция y=arctg⁡x{\displaystyle y=\operatorname {arctg} x} является строго возрастающей.

• tg(arctgx)=x{\displaystyle \operatorname {tg} \,(\operatorname {arctg} \,x)=x} при x∈R,{\displaystyle x\in \mathbb {R} ,}
• arctg(tgy)=y{\displaystyle \operatorname {arctg} \,(\operatorname {tg} \,y)=y} при −π2<y<π2,{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}},}
• D(arctgx)∈R,{\displaystyle D(\operatorname {arctg} \,x)\in \mathbb {R} ,}
• E(arctgx)=(−π2;π2){\displaystyle E(\operatorname {arctg} \,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)}

Свойства функции arctg

• arctg(−x)=−arctgx{\displaystyle \operatorname {arctg} \,(-x)=-\operatorname {arctg} \,x} (функция нечётная).
• arctgx>{\displaystyle \operatorname {arctg} \,x>0} при x>{\displaystyle x>0.}
• arctgx={\displaystyle \operatorname {arctg} \,x=0} при x={\displaystyle x=0.}
• arctgx<{\displaystyle \operatorname {arctg} \,x<0} при x<{\displaystyle x<0.}
• arctgx={arccos⁡11+x2,x⩾−arccos⁡11+x2,⩽x{\displaystyle \operatorname {arctg} \,x=\left\{{\begin{matrix}\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad x\geqslant 0\\-\arccos {\frac {1}{\sqrt {1+x^{2}}}},\qquad 0\leqslant x\end{matrix}}\right.}
• arctgx={arcctg1x,x>arcctg1x−π,⩽x{\displaystyle \operatorname {arctg} \,x=\left\{{\begin{matrix}\operatorname {arcctg} \,{\frac {1}{x}},x>0\\\operatorname {arcctg} \,{\frac {1}{x}}-\pi ,\qquad 0\leqslant x\end{matrix}}\right.}

Получение функции arctg

Дана функция y=tgx.{\displaystyle y=\operatorname {tg} \,x.} На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arctgx{\displaystyle y=\operatorname {arctg} \,x} функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (−π2;π2).{\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right).} На этом отрезке y=tgx{\displaystyle y=\operatorname {tg} \,x} строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале (−π2;π2){\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)} существует обратная функция y=arctgx{\displaystyle y=\operatorname {arctg} \,x}, график которой симметричен графику y=tgx{\displaystyle y=\operatorname {tg} \,x} на отрезке (−π2;π2){\displaystyle \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)} относительно прямой y=x.{\displaystyle y=x.}

Формулы понижения степени тригонометрических функций

Вторая степень

\sin ^2 \alpha = \dfrac{1-\cos(2\alpha)}{2}\cos ^2 \alpha = \dfrac{1+\cos(2\alpha)}{2}\tg ^2 \alpha = \dfrac{1-\cos(2\alpha)}{1+\cos(2\alpha)}\ctg ^2 \alpha = \dfrac{1+\cos(2\alpha)}{1-\cos(2\alpha)}(\sin \alpha- \cos \alpha)^2=1-\sin(2 \alpha)(\sin \alpha+ \cos \alpha)^2=1+\sin(2 \alpha)

Третья степень

\sin ^3 \alpha = \dfrac{3 \cdot \sin(\alpha)-\sin(3 \alpha)}{4}\cos ^3 \alpha = \dfrac{3 \cdot \cos(\alpha)+\cos(3 \alpha)}{4}\tg ^3 \alpha = \dfrac{3 \cdot \sin (\alpha)-\sin(3 \alpha)}{3 \cdot \cos (\alpha)+\cos(3 \alpha)}\ctg ^3 \alpha = \dfrac{3 \cdot \cos (\alpha)+\cos(3 \alpha)}{3 \cdot \sin (\alpha)-\sin(3 \alpha)}

Четвёртая степень

\sin ^4 \alpha = \dfrac{3-4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}\cos ^4 \alpha = \dfrac{3+4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}

Пятая степень

\sin ^5 \alpha = \dfrac{10 \cdot \sin(\alpha)-5 \cdot \sin(3 \alpha)+\sin(5 \alpha)}{16}\cos ^5 \alpha = \dfrac{10 \cdot \cos(\alpha)+5 \cdot \cos(3 \alpha)+\cos(5 \alpha)}{16}

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона: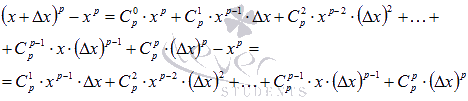

Следовательно,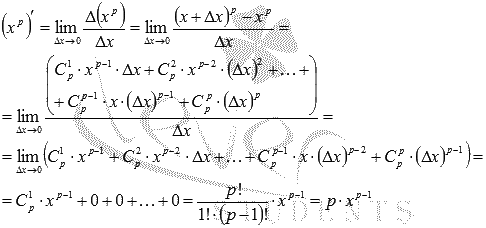

Этим доказана формула производной степенной функции для натурального показателя.

При доказательстве формулы для любого действительного p, отличного от нуля, воспользуемся логарифмической производной (не путайте с производной логарифмической функции). Для понимания процесса, рекомендуем сначала ознакомиться с , а также разобраться с разделами теории производная неявно заданной функции и производная сложной функции.

Следует рассмотреть два случая: при положительных x и отрицательных x.

Сначала будем полагать . В этом случае . Выполним логарифмирование равенства по основанию e и применим свойство логарифма:

Пришли к неявно заданной функции. Находим ее производную: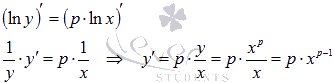

Осталось провести доказательство для отрицательных x.

Когда показатель p представляет собой четное число, то степенная функция определена и при , причем является четной (смотрите раздел основные элементарные функции, их свойства и графики). То есть, . В этом случае и также можно использовать доказательство через логарифмическую производную.

Когда показатель p представляет собой нечетное число, то степенная функция определена и при , причем является нечетной. То есть, . В этом случае и логарифмическую производную использовать нельзя. Для доказательства формулы в этом случае можно воспользоваться правилами дифференцирования и правилом нахождения производной сложной функции: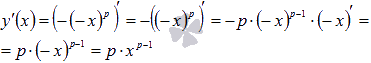

Последний переход возможен в силу того, что если p — нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, для отрицательных x справедливо равенство .

Таким образом, формула производной степенной функции доказана для любого действительного p.

Пример.

Найти производные функций .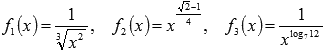

Решение.

Первую и третью функцию приведем к табличному виду , используя свойства степени, и применим формулу производной степенной функции: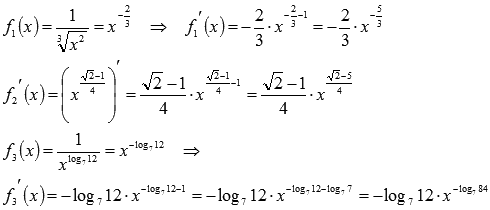

Примеры и задачи

Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:

• arcsin (sinx)=x;
• arccos (cosx)=x;
• arctg (tgx)=x;
• arcctg (ctgx)=x.

Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке , тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.

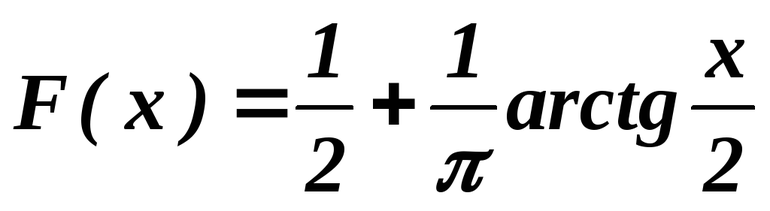
Известно, аrcsin sin (-15)= -15 град., arccos (cos (2π/3))=2π/3, arctg (tg (0,2))=0,2. Нужно отметить, что выражение arcsin (sin α) справедливо на отрезке −π/2≤α≤π/2. Но равенство arcsin (sin α)=α имеет смысл только при соблюдении этого условия. Нельзя утверждать, что arcsin (sin (7π/4))=7π/4, так как 7π/4 не принадлежит указанному интервалу (−π/2-π/2).

Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).

Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.

Если «арка» берется от отрицательного числа?

Всё ли я сказал про «арки»? Почти что да! Остался вот какой момент.

Что делать, если «арка» берётся от отрицательного числа?

Лезть в таблицу – как бы не так! Для арок выполняются следующие формулы:

• \( \displaystyle \text{arcsin}\left( -\alpha \right)=-\text{arcsin}\alpha \)
• \( \displaystyle \text{arctg}\left( -\alpha \right)=-\text{arctg}\alpha \)

И внимание!!!

• \( \displaystyle \text{arcctg}\left( -\alpha \right)=\text{ }\!\!\pi\!\!\text{ }-\text{arcctg}\alpha \)
• \( \displaystyle \text{arccos}\left( -\alpha \right)=\text{ }\!\!\pi\!\!\text{ }-\text{arccos}\alpha \)

Чтобы запомнить, ориентируемся на обычные тригонометрические функции: грубо говоря, синус и тангенс мы смотрим на тригонометрической окружности по вертикальной оси, а косинус и котангенс – по горизонтальной.

Соответственно, для арксинуса и арктангенса выбираем две четверти по вертикали: первую и четвёртую (минусик выносится из аргумента и ставится перед функцией), а для арккосинуса и арккотангенса – по горизонтали: первую и вторую.

В первой и второй четвертях аргумент уже не может быть отрицательным, поэтому и получаются формулы не совсем похожими.

Формулы произведения тригонометрических функций

\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}

Решение 3-х примеров для самостоятельной работы

• Ре­ши­те урав­не­ние \( \displaystyle sin\frac{\pi x}{3}=0,5\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.
• Ре­ши­те урав­не­ние \( \displaystyle tg\frac{\pi \left( {x}-6 \right)}{6}=\frac{1}{\sqrt{3}}\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.
• Ре­ши­те урав­не­ние \( \displaystyle sin\frac{\pi \left( 2{x}-3 \right)}{6}=-0,5\). В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

Готов? Проверяем. Я не буду подробно описывать весь алгоритм решения, мне кажется, ему и так уделено достаточно внимания выше.

Вывод формулы производной котангенса

Чтобы вывести формулу производной котангенса, мы воспользуемся следующими математическими фактами:1)
Выражением котангенса через косинус и синус :(1)
;
2)
Значением производной косинуса :(2)
;
3)
Значением производной синуса :(3)
;
4)
Формулой производной частного :(4)
;
5)
Тригонометрической формулой :(5)
.

Применяем эти формулы и правила к производной котангенса..

Тем самым мы получили формулу производной котангенса.

Формула производной дроби (4) справедлива для тех значений переменной x
,
для которых существуют производные функций и и для которых знаменатель дроби не обращается в нуль:.
В нашем случае,
.
Поскольку производные косинуса и синуса определены для всех значений переменной x
,
то формула производной котангенса справедлива для всех x
,
кроме точек, в которых синус равен нулю. То есть кроме точек,
где — целое число. Сама функция y = ctg
x
определена для всех x
,
кроме точек.
Поэтому производная котангенса определена на всей области определения функции котангенс
.