Формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом

Алгоритм вычисления арксинусов и других «арок»

Смотрим на то, что стоит под «аркой» – какое там число
Смотрим, какая у нас «арка» – для синуса ли, или для косинуса, тангенса или котангенса
Смотрим, чему равен угол (1 четверти), для которого синус, косинус, тангенс, котангенс равен числу, стоящему под аркой
Записываем ответ

Вот простой пример вычисления аркосинуса:

Решение:

Под аркой число $ \displaystyle \frac{\sqrt{3}}{2}$
Арка для функции – косинус!
Косинус какого угла равен $ \displaystyle \frac{\sqrt{3}}{2}$? Угла $ \displaystyle \frac{\pi }{6}$ (или $ \displaystyle 30$ градусов!)
Тогда $ \displaystyle \arccos \left( \frac{\sqrt{3}}{2} \right)=\frac{\pi }{6}$

Сам посчитай:

$ \displaystyle \ arctg\left( \frac{1}{\sqrt{3}} \right)$
$ \displaystyle \arcsin \left( \frac{\sqrt{3}}{2} \right)$

Ответы:

Формулы тройного угла

Формулы тройного угла обычно попадаются на математических олимпиадах или вступительных экзаменах в математические ВУЗы. Учить их необязательно, но знать о существовании полезно, тем более, что они достаточно легко выводятся.
$$\cos(3*\alpha)=\cos^3(\alpha)-3*\sin^2(\alpha)*\cos(\alpha)=-3*\cos(\alpha)+4*\cos^3(\alpha);$$
$$\sin(3*\alpha)=3*\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=3*\sin(\alpha)-4*\sin^3(\alpha);$$
$$tg(3*\alpha)=\frac{3*tg(\alpha)-tg^3(\alpha)}{1-3*tg^2(\alpha)};$$
$$ctg(3*\alpha)=\frac{ctg^3(\alpha)-3*ctg(\alpha)}{3*ctg^2(\alpha)-1};$$

Выведем эти формулы, использую формулы сложения. Начнем с косинуса тройного угла:
$$\cos(3*\alpha)=\cos(2\alpha+\alpha)=\cos(2\alpha)*\cos(\alpha)-\sin(2\alpha)*\sin(\alpha)=$$
$$=(\cos^2(\alpha)-\sin^2(\alpha))*\cos(\alpha)-2\sin(\alpha)*\cos(\alpha)*\sin(\alpha)=$$
$$=\cos^3(\alpha)-\sin^2(\alpha)*\cos(\alpha)-2\sin^2(\alpha)*\cos(\alpha)=$$
$$=\cos^3(\alpha)-3\sin^2(\alpha)*\cos(\alpha);$$

Если расписать $sin^2(\alpha)=1-\cos^2(\alpha)$, то получим еще один вариант формулы тройного угла:
$$\cos(3*\alpha)=cos^3(\alpha)-3\sin^2(\alpha)*\cos(\alpha)=cos^3(\alpha)-3(1-\cos^2(\alpha))*\cos(\alpha)=$$
$$=4\cos^3(\alpha)-3\cos(\alpha);$$

Аналогично выводится формула синуса тройного угла:
$$\sin(3\alpha)=\sin(2\alpha+\alpha)=\sin(2\alpha)*\cos(\alpha)+\sin(\alpha)*\cos(2\alpha)=$$
$$=2\sin(\alpha)*\cos(\alpha)*\cos(\alpha)+\sin(\alpha)*(\cos^2(\alpha)-\sin^2(\alpha))=$$
$$=2\sin(\alpha)*\cos^2(\alpha)+\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=3\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha);$$
Распишем по основному тригонометрическому тождеству $\cos^2(\alpha)=1-\sin^2(\alpha)$ и подставим:
$$\sin(3\alpha)=3\sin(\alpha)*\cos^2(\alpha)-\sin^3(\alpha)=$$
$$=3\sin(\alpha)*(1-\sin^2(\alpha))-\sin^3(\alpha)=3\sin(\alpha)-4\sin^3(\alpha);$$

Для тангенса и котангенса формулы тройного угла здесь выводить не будем, так как они достаточно редки. Но в качестве упражнения можете сами выполнить вывод, представив тангенс или котангенс по определению: через отношение синуса тройного угла к косинусу тройного угла или наоборот соотвественно.

Формулы тройного угла обычно используются при преобразовании сложных тригонометрических выражений. Например, на вступительных экзаменах в МФТИ любят давать тригонометрические уравнения на тройной угол и больше.

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

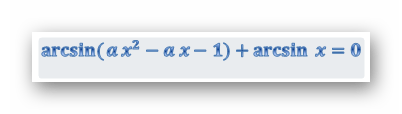
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

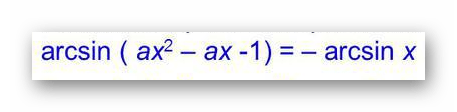
Если вспомнить формулу arcsin (sin α) = α
, то можно свести поиск ответов к решению системы из двух уравнений:

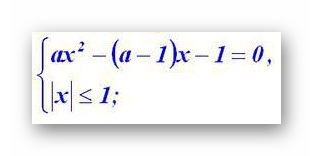
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x . При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

Область определения функции: .
Область значений функции: .
Функция является нечетной: .
Функция возрастает.
Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

Область определения функции: .
Область значений функции: .
Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
Функция убывает.
Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

Формулы половинного угла.

Синус половинного угла. Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части.

Данное правило справедливо также для других формул, приведенных ниже.
Косинус половинного угла:
Тангенс половинного угла:
Котангенс половинного угла:
Выражение синуса через тангенс половинного угла:
Выражение косинуса через тангенс половинного угла:
Выражение тангенса через тангенс половинного угла:
Выражение котангенса через тангенс половинного угла:

Формулы приведения.

Функция / угол в рад.	π/2 – α	π/2 + α	π – α	π + α	3π/2 – α	3π/2 + α	2π – α	2π + α
sin	cos α	cos α	sin α	– sin α	– cos α	– cos α	– sin α	sin α
cos	sin α	– sin α	– cos α	– cos α	– sin α	sin α	cos α	cos α
tg	ctg α	– ctg α	– tg α	tg α	ctg α	– ctg α	– tg α	tg α
ctg	tg α	– tg α	– ctg α	ctg α	tg α	– tg α	– ctg α	ctg α
Функция / угол в °	90° – α	90° + α	180° – α	180° + α	270° – α	270° + α	360° – α	360° + α

Подробное описание формул приведения.

Основные тригонометрические формулы.

Основное тригонометрическое тождество:

sin2α+cos2α=1

Данное тождество − результат применения теоремы Пифагора к треугольнику в единичном тригонометрическом круге.

Соотношение между косинусом и тангенсом:

1/cos2α−tan2α=1 или sec2α−tan2α=1.

Данная формула является следствием основного тригонометрического тождества и получается из него делением левой и правой части на cos2α. Предполагается, что α≠π/2+πn,n∈Z.

Соотношение между синусом и котангенсом:

1/sin2α−cot2α=1 или csc2α−cot2α=1.

Эта формула также следует из основного тригонометрического тождества (получается из него делением левой и правой части на sin2α. Здесь предполагается, что α≠πn,n∈Z.

tanα=sinα/cosα,

где α≠π/2+πn,n∈Z.

cotα=cosα/sinα,

где α≠πn,n∈Z.

tanα⋅cotα=1,

где α≠πn/2,n∈Z.

Определение косеканса:

cscα=1/sinα,α≠πn,n∈Z

Тригонометрические неравенства.

Простейшие тригонометрические неравенства:

sinx > a, sinx ≥ a, sinx < a, sinx ≤ a,

cosx > a, cosx ≥ a, cosx < a, cosx ≤ a,

tanx > a, tanx ≥ a, tanx < a, tanx ≤ a,

cotx > a, cotx ≥ a, cotx < a, cotx ≤ a.

Прочие формулы с обратными функциями

Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач. Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.

Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:

sin 2 α 2 = 1 — cos α 2

Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:

sin α 2 = 1 — cos α 2

Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:

sin a r c cos α 2 = 1 — cos ( a r c cos α ) 2 ⇔ sin a r c cos α 2 = 1 — α 2

Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:

a r c cos α 2 = a r c sin 1 — α 2

Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них

Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове

В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

Функция определена на отрезке .
ОДЗ для arccos — .
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.

Задание 1.
Укажите функции изображенные на рисунке.

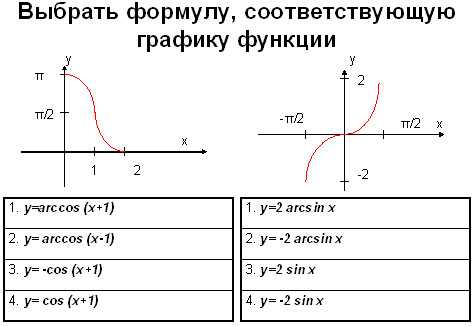
Ответ:
рис. 1 – 4, рис.2 — 1.

В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.

Арктангенс и арккотангенс − теория, примеры и решения

Функция арктангенс и ее график

Функция тангенс определена в интервале кроме точек , . и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

, , , и т.д.

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

y=arctg x.

(1)

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арктангенс.

Область определения функции: .
Область значений функции: .
Функция является нечетной: .
Функция возрастает.
Функция непрерывна.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

(3)

Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OM_t₁ c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OT_t пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Как известно, функция котангенс определена в интервале кроме точек -2π, —π 0, π, 2π. и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

y=arcctg x.

(4)

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

Область определения функции: .
Область значений функции: .
Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
Функция убывает.
Функция непрерывна.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

(6)

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x
зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

Функция определена на отрезке .
ОДЗ для arccos — .
График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
Y = 0 при x = 1.
Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Задание 1.
Укажите функции изображенные на рисунке.

Ответ:
рис. 1 – 4, рис.2 — 1.

Обратные функции отрицательного аргумента

Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.

arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x

Поскольку то умножив на -1
, имеем: или Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.

Аналогично для остальных функций.arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x

arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x

arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x

Основное тригонометрическое тождество

Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:

Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:

АВ2 + ОВ2 = ОА2

Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:

sin2α + соs2α = 1

Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.

Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?

Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:

sin2α + соs2α = 1

0,82 + соs2α = 1

0,64 + соs2α = 1

соs2α = 1 – 0,64

соs2α = 0,36

соsα = – 0,6 или соsα = 0,6

Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.

Ответ: 0,6.

Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:

По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.

Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.

Решение.

sin2α + соs2α = 1

0,282 + sin2α = 1

0,0784 + sin2α = 1

sin2α = 1 – 0,0784

sin2α = 0,9216

sin α = –0,96 или sin α = 0,96

Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.

Ответ: – 0,96.

Задание. Найдите tgα, если sinα = 5/13 и π/2 < α < π.

Решение. Здесь задача уже в два действия! Сначала определим соsα:

sin2α + соs2α = 1

соs2α = 1 – sin2α = 1 – (5/13)2 = 169/169 – 25/169 = 144/169

соsα = – 12/13 или соsα = 12/13

Условие π/2 < α < π указывает на то, что угол относится ко II четверти, в которой косинус отрицателен, поэтому соsα = – 12/13.

Далее находим тангенс, просто деля синус на косинус:

tgα = sinα:соsα = (5/13):(12/13) = (5/13)•(13/12) = 5/12

Ответ: 5/12

Рассмотренный пример показал нам, что, зная синус, можно рассчитать не только косинус, но и тангенс. А возможно ли совершить обратное действие, найти по тангенсу синус или косинус? Да, но для этого нужно получить новую тригонометрическую формулу.

Запишем тождество

sin2α + соs2α = 1

Далее поделим его на величину соs2α:

Крайнее левое слагаемое – это величина tg2α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:

В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin2α:

Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.

Решение.

Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:

Так как угол относится к III четверти, где косинус отрицателен, то

соsα = – 0,8

Синус угла найдем, используя основное тригон-кое тождество:

sin2α + соs2α = 1

sin2α = 1 – соs2α = 1 – (– 0,8)2 = 1 – 0,64 = 0,36

sinα = – 0,6 или sinα = 0,6

С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6

Ответ: sinα = – 0,6; соsα = – 0,8.

Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin2α + соs2α = 1 несложно получить из выражения

sin2α = 1 – соs2α

соs2α = 1 – sin2α

которые помогают в работе с длинными ф-лами.

Задание. Упростите выражение

4sin2α + 9соs2α – 6

таким образом, чтобы в нем не содержалось синуса.

Решение. Произведем замену sin2α = 1 – соs2α:

4sin2α+ 9соs2α – 6 = 4(1 – соs2α)+ 9соs2α – 6 =

= 4 – 4 соs2α + 9соs2α – 6 = 5соs2α – 2

Видим, что получилось значительно более простое выражение.

Ответ: 5соs2α – 2.

Задание. Избавьтесь от синуса в выражении

sin4α – соs4α

Решение. Воспользуемся ф-лой :

sin4α – соs4α = (sin2α – соs2α)(sin2α + соs2α) = (sin2α – соs2α)•1 =

= 1 – соs2α– соs2α = 1 – 2 соs2α

Ответ:1 – 2 соs2α.

Задание. Упростите дробь

Решение.

Ответ: ctg6α.

Формулы двойного угла (аргумента)

\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}

VI группа. Формулы понижения степени

cos2α = 1 + cos2α_________ 2;

sin2α = 1 − cos2α_________ 2;

cos3α = 3cosα + cos3α____________4;

sin3α = 3sinα − sin3α____________4.

Первые две формулы этой группы очень нужны. Применяются часто при решении тригонометрических уравнений, в том числе уровня единого экзамена, а также при вычислении интегралов, содержащих подинтегральные функции тригонометрического типа.

2cos2α = 1 + cos2α; 2 sin2α = 1 − cos2α,

Необходимость в использовании следующих двух формул (с кубами функций) на экзаменах встречается гораздо реже. В другой обстановке у Вас всегда будет время воспользоваться черновиком. При этом возможны следующие варианты:
1) Если Вы помните последние две формулы III-ей группы, то пользуйтесь ими, чтобы выражать sin3α и cos3α путем несложных преобразований.
2) Если в последних двух формулах этой группы Вы заметили элементы симметрии, которые способствуют их запоминанию, то записывайте «эскизы» формул на черновике и проверяйте их по значениям основных углов.
3) Если, кроме того, что такие формулы понижения степени существуют, Вы о них ничего не знаете, то решайте задачу поэтапно, исходя из того, что sin3α = sin2α·sinα и прочих выученных формул. Потребуются формулы понижения степени для квадрата и формулы преобразования произведения в сумму.

Если рекомендации понятны, нажмите кнопку , чтобы убрать «лишние» формулы.