Логарифмы

Свойства логарифмов

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b: log a b=c⇔ a c =b (a>0,a≠1,b>0)

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1

Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество

a log a b =b (a>0,a≠1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1

Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма

log a a=1 (a>0,a≠1) (3) log a 1=0 (a>0,a≠1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) (5)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение log a (f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f(x)+ log a g(x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма

log a b p =p log a b (a>0,a≠1,b>0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a (f (x) 2 =2 log a f(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).

a log a b =b (a>0,a≠1)

log a a=1 (a>0,a≠1)

log a 1=0 (a>0,a≠1)

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0)

log a b p =p log a b (a>0,a≠1,b>0)

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1)

log a b= 1 log b a (a>0,a≠1,b>0,b≠1)

Десятичный логарифм

Определение 1

Десятичным логарифмом называют логарифм, который имеет в основании число $10$.

• Десятичный логарифм вматематике принято обозначать $lg$:
• $lg ⁡a=log_{10}⁡a$.
• Название десятичного логарифма происходит именно от его основания, которое равняется десяти.
• Иногда можно встретить следующее обозначение десятичного логарифма:
• $log ⁡a$.

Замечание 1

Согласно определению логарифма можно сделать вывод, что десятичный логарифм $lg ⁡a$ является решением показательного уравнения $10^b=a$.

Свойства десятичного логарифма

1. Т.к. логарифм по любому основанию от $1$ равен $0$, то и десятичный логарифм единицы равен $0$:

   $lg ⁡1=0$.

2. Десятичный логарифм от числа $10$ равен единице:

   $lg ⁡10=1$.

3. Десятичный логарифм произведения двух чисел равен сумме десятичных логарифмов от этих чисел:

   $lg ⁡(ab)=lg ⁡a+lg ⁡b$.

4. Десятичный логарифм частного двух чисел равен разнице десятичных логарифмов этих чисел:

   $lg frac{a}{b}=lg ⁡a-lg ⁡b$.

5. Десятичный логарифм степени числа может быть представлен в виде произведения показателя степени на десятичный логарифм подлогарифмического числа:

   $lg⁡ a^s=s cdot lg ⁡a$.

Ничего непонятно?

Попробуй обратиться за помощью к преподавателям

Пример 1

1. Упростить выражение $frac{2 lg ⁡40-lg ⁡16}{lg ⁡50-frac{1}{2} lg ⁡25}$.
2. Решение.
3. Применим к первому логарифму в числителе и в знаменателе свойство логарифма произведения, а ко второму логарифму числителя и знаменателя – свойство логарифма степени:
4. $frac{2 lg ⁡40-lg ⁡16}{lg ⁡50-frac{1}{2} lg ⁡25}=frac{2(lg ⁡4+lg ⁡10 )-lg 4^2}{lg ⁡5+lg ⁡10-frac{1}{2} lg 5^2}=$
5. откроем скобки и приведем подобные слагаемые, а также применим свойство $lg ⁡10=1$:
6. $=frac{2 lg ⁡4+2-2 lg ⁡4}{lg ⁡5+1-frac{1}{2} cdot 2 lg ⁡5}=frac{2}{lg ⁡5+1-lg ⁡5}=2$.
7. Ответ: $frac{2 lg ⁡40-lg ⁡16}{lg ⁡50-frac{1}{2} ln ⁡25}=2$.

Пример 2

• Вычислить значение логарифмического выражения $lg ⁡200+lg frac{1}{20}$.
• Решение.
• Применим формулу суммы логарифмов:
• $lg ⁡200+lg frac{1}{20}=lg ⁡(200 cdot frac{1}{20})=lg ⁡10=1$.
• Ответ: $lg ⁡200+lg frac{1}{20}=1$.

Пример 3

1. Вычислить значение логарифмического выражения $2 ln frac{1}{e^2}+3 lg ⁡10000$.
2. Решение.
3. Применим свойство логарифма степени:
4. $2 ln frac{1}{e^2}+3 lg ⁡10000=2 ln e^{-2}+3 lg 10^4=2 cdot (-2) ln ⁡e+3 cdot 4 lg ⁡10=-4 ln ⁡e+12 lg ⁡10=$
5. теперь применим свойство логарифма, у которого основание равно подлогарифмическому числу:
6. $=-4 cdot 1+12 cdot 1=8$.
7. Ответ: $2 ln frac{1}{e^2}+3 lg ⁡10000=8$.

Пример 4

• Упростить логарифмическое выражение $lg frac{1}{8}-3 lg ⁡4$.
• Решение.
• Применим свойство логарифма степени:
• $lg frac{1}{8}-3 lg ⁡4=lg 2^{-3}-3 lg⁡ 2^2=-3 lg ⁡2-3 cdot 2 lg ⁡2=-9 lg ⁡2$.
• Ответ: $lg frac{1}{8}-3 lg ⁡4=-9 lg ⁡2$.

Пример 5

1. Вычислить значение логарифмического выражения $3 lg ⁡0,09-2 lg ⁡27$.
2. Решение.
3. Применим к обоим логарифмам свойство логарифма степени:
4. $3 lg frac{9}{10^2}-2 lg ⁡27=3 lg (frac{3}{10})^2-2 lg 3^3=3 cdot 2 lg frac{3}{10}-2 cdot 3 lg ⁡3=6 lg frac{3}{10}-6 lg ⁡3=$
5. применим к первому логарифму свойство логарифма частного:
6. $=6(lg ⁡3-lg ⁡10 )-6 lg ⁡3=$
7. откроем скобки и приведем подобные слагаемые:
8. $=6 lg ⁡3-6 lg ⁡10-6 lg ⁡3=-6$.
9. Ответ: $3 lg ⁡0,09-2 lg ⁡27=-6$.

Пример 6

• Упростить логарифмическое выражение $lg ⁡0,81-2 lg ⁡9$.
• Решение.
• Применим ко второму логарифму свойство логарифма степени, внеся число $2$ под знак логарифма:
• $lg ⁡0,81-lg 9^2=lg ⁡0,81-lg ⁡81=$
• применим формулу разности логарифмов:
• $=lg frac{0,81}{81}=lg ⁡0,01=$
• запишем число под знаком логарифма как $10$ в степени:
• $=lg 10^{-2}=$
• применим формулу логарифма степени:
• $=-2 lg ⁡10=-2$.
• Ответ: $lg ⁡0,81-2 lg ⁡9=-2$.

Пример 7

1. Вычислить значение логарифмического выражения $frac{2 lg ⁡2-lg ⁡16}{lg 4+lg ⁡16}$.
2. Решение.
3. Внесем число $2$ в числителе под знак логарифма:
4. $frac{2 lg ⁡2-lg ⁡16}{lg 4+lg ⁡16}=frac{lg 2^2-lg ⁡16}{lg 4+lg ⁡16}=$
5. применим формулы разности и суммы логарифмов:
6. $=frac{lg frac{4}{16}}{lg⁡ (4 cdot 16)} =frac{lg frac{1}{4}}{lg ⁡64} =$
7. применим формулу логарифма степени, записав число под знаком логарифма как число $4$ в степени:
8. $=frac{lg 4^{-1}}{lg 4^3} =frac{-lg ⁡4}{3 lg ⁡4}=-frac{1}{3}$.
9. Ответ: $frac{2 lg ⁡2-lg ⁡16}{lg 4+lg ⁡16} =-frac{1}{3}$.

Пример 8

• Преобразовать логарифмическое выражение $lg frac{100}{e}$.
• Решение.
• Применим формулу логарифма частного:
• $lg frac{100}{e}=lg ⁡100-lg ⁡e=$
• к первому логарифму применим формулу логарифма степени:
• $=lg 10^2-lg ⁡e=2 lg ⁡10-lg ⁡e=$
• применив свойство значения логарифма с одинаковым основанием и подлогарифмическим числом, получим:
• $=2 cdot 1-lg ⁡e=2-lg ⁡e$.
• Ответ: $lg frac{100}{e}=2-lg ⁡e$.

40.500. Логарифмические уравнения

Логарифмом числа $ b $ по основанию $ a(c=log_{a}b) $ называется такой показатель степени $ c $, в которую нужно возвести $ a $, чтобы получить $ b $ (то есть $ a^{c}=b $). При этом задаются ограничения: $ a>0, \; a \neq 1, \; b>0$. Значение $ c $ логарифма может быть любым.

Вычислите:

$ log_{3}27, \; log_{\frac {1}{3}}27 $

1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.

$ 3=log_{3}27 $

2. При возведении $ \big(\frac{1}{3} \big)^{-3}=27 $ значит, $ -3=log_{\frac{1}{3}}27 $

Ответ: 3; -3.

Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.

Пусть $ y=log_{2}x $. Подставим вместо $ x $ разные числа и определим соответствующие значения переменной $ y $.

Отметим координаты точек на плоскости и соединим их плавной линией.

Легко заметить, что функция все время возрастает. Такое поведение характерно для всех логарифмических функций с основанием больше единицы.

Пусть теперь $ y=log_{\frac{1}{2}}x $. Составим таблицу значений для этого случая.

Тогда график функции будет выглядеть следующим образом.

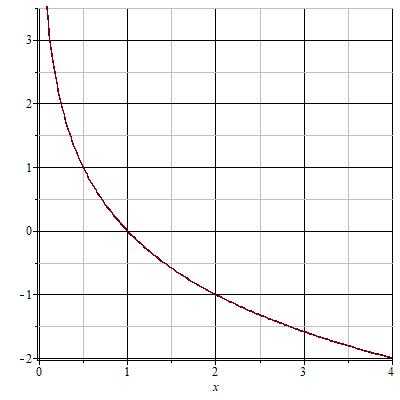
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.

Графики всех логарифмических функций проходят через точку с координатами (1;0).

Особыми знаками принято обозначать логарифмы с основанием десять $ log_{10}a=lga $ и логарифмы с натуральным основанием $ e \approx 2.72 \; log_{e} \; a=In \; a $.

Свойства логарифмов

Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.

Правило	Формула
Логарифм 1 по любому основанию равен 0.	$log_{a}1=0$
Логарифм числа по равному ему основанию равен 1.	$log_{a}a=1$
Основное логарифмическое тождество. При разведении основание в степень логарифма получается подлогарифмическое выражение.	$a^{log_{a}b}=b$
Логарифм произведения равен сумме логарифмов.	$log_{a}bc=log_{a}b+log_{a}c$

Логарифм частного равен разности логарифмов.	$log_{a} \frac{b}{c}=log_{a}b-log_{a}c$
Показатель степени можно выносить из подлогарифмического выражения за знак логарифма.	$log_{a}b^{p}=plog_{a}b$
Показатель степени можно выносить из основания логарифма, возводя его в -1 степень.	$log_{a^{a}}b=\frac{1}{q}log_{a}b$
Можно представить логарифмов в виде частного логарифмов с новым основанием.	$log_{a}b=\frac {log_{c}b}{log_{c}a}$
Если поменять местами подлогарифмическое выражение и основание логарифма, получится логарифм, обратный исходному.	$log_{a}b=\frac {1}{log_{b}a}$

Используем рассмотренные свойства для решения некоторых задач.

Пример 2

Вычислите $ log_{5}3125 $

1. Представим $ 3125=5^{5} $.

2. Вынесем степень из—под знака логарифма:

$ log_{5}3125=log_{5}5^{5}=5log_{5}5 $

3. Логарифм числа по равному ему основанию равен 1:

$ 5log_{5}5=5 $

Ответ: 5.

Пример 3

Вычислите $ 5^{2+log_{5}3} $

1. Воспользуемся свойством степеней:

$ 5^{2+log_{5}3}=5^{2} \cdot 5^{log_{5}3} $

2. Используем основное логарифмическое тождество:

$ 5^{2} \cdot 5^{log_{5}3}=25 \cdot 3=75 $

Ответ: 75.

Пример 4

Вычислите $ lg125+lg8 $

1. Воспользуемся формулой для суммы логарифмов:

$ lg125+lg8=lg1000 $

2. Представим 1000 = 103 и вынесем 3 за знак логарифма:

$ lg1000=lg10^{3}=3lg10 $

3. Воспользуемся тем, что $ lg10=1 $.

Ответ: 3.

Пример 5

Вычислить $ log_{36}84-log_{36}14 $.

1. Воспользуемся формулой для частного логарифмов:

$ log_{36}84-log_{36}14=log_{36}6 $

2. Преобразуем основание логарифма 36 = 62 и вынесем, «перевернув», вынесем показатель:

$ log_{36}6=log_{6^{2}}6= \frac {1}{2}log_{6}6 $

3. Воспользуемся тем, что $ log_{6}6=1 $

Ответ: 0,5.

Пример 6

Вычислите $ \frac {lg8+lg18}{2lg2+lg3} $.

1. Применим в числителе формулу для сумы логарифмов:

$ \frac {lg8+lg18}{2lg2+lg3}=\frac {lg144}{2lg2+lg3} $

2. В знаменателе внесем 2 под знак логарифма:

$ 2lg2=lg2^{2}=lg4 $

3. Воспользуемся формулой суммы логарифмов для знаменателя:

$ \frac {lg144}{lg4+lg3}=\frac {lg144}{lg12} $

4. Перейдем от частного к логарифму с основанием 12:

$ \frac {lg144}{lg12}=log_{12}144 $

5. Представим 144 = 122, вынесем степень за знак логарифма и воспользуемся соотношением $ log_{12}12=1 $

$ log_{12}144=log_{12}12^{2}=2log_{12}12=2 $

Ответ: 2.

Кроме выражений с числами, на экзамене могут встретиться выражения, содержащие переменные. В этом случае можно использовать те же формулы и правила.

Пример 7

Вычислите $ log_{125}\frac {a^{2} \cdot a}{a^{3}} $

1. Преобразуем отдельно подлогарифмическое выражение:

$ \frac {a^{2} \cdot a}{a^{3}}=a^{2+1-3}=a^{0}=1 $

2. Логарифм 1 по любому основанию равен 0:

$ log_{125}1=0 $

Ответ: 0.

ПрочитаноОтметь, если полностью прочитал текст

Как посчитать логарифм

Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма \(log_{a}(b)\) существует только при положительных значениях основания \(a\) и аргумента \(b\). И, кроме этого, на основание накладывается условие, что оно не должно быть равно \(1\).

Почему так? Это следует из определения показательной функции. Показательная функция не может быть равна \(0\) и не может быть меньше \(0\). А основание не равно \(1\), потому что тогда логарифм теряет смысл – ведь \(1\) в любой степени это будет \(1\).

В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.

Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д

Так как (вспоминайте определение отрицательной степени):

Теперь давайте разберем общий алгоритм вычисления логарифмов:

• Во-первых, постарайтесь представить основание и аргумент под логарифмом в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
• Разобраться, в какую степень \(x\) нужно возвести основание, чтобы получить аргумент. Когда у вас и там, и там степени с одинаковым основанием, посчитать значение логарифма становится проще.
• \(x\) и будет искомым значением логарифма.

Разберем на примерах.

Пример 1Посчитать логарифм от \(9\) по основанию \(3\): \(\quad log_{3}(9)=?\)

• Сначала представим аргумент и основание в виде степеней тройки:
  $$ 3=3^1, \qquad 9=3^2;$$
  $$log_{3}(9)=log_{3^1}(3^2);$$
• Теперь надо разобраться в какую степень \(x\) нужно возвести \(3^1\), чтобы получить \(3^2\)
  $$ (3^1)^x=3^2, $$
  $$ 3^{1*x}=3^2, $$
  $$ 1*x=2,$$
  $$ x=2.$$
• Вот мы и решили:
  $$log_{3}(9)=2.$$

Пример 2Вычислить логарифм от \(\frac{1}{125}\) по основанию \(5\): \(\quad log_{5}(\frac{1}{125})=?\)

• Представим аргумент и основание в виде степени пятерки:
  $$ 5=5^1, \qquad \frac{1}{125}=\frac{1}{5^3}=5^{-3};$$
  $$log_{5}(\frac{1}{125})=log_{5^1}(5^{-3});$$
• В какую степень \(x\) надо возвести \(5^1\), чтобы получить \(5^{-3}\):
  $$ (5^1)^x=5^{-3}, $$
  $$ 5^{1*x}=5^{-3},$$
  $$1*x=-3,$$
  $$x=-3.$$
• Получили ответ:
  $$ log_{5}(\frac{1}{125})=-3.$$

Пример 3Вычислить логарифм от \(4\) по основанию \(64\): \(\quad log_{64}(4)=?\)

• Представим аргумент и основание в виде степени двойки:
  $$ 64=2^6, \qquad 4=2^2;$$
  $$log_{64}(4)=log_{2^6}(2^2);$$
• В какую степень \(x\) надо возвести \(2^6\), чтобы получить \(2^{2}\):
  $$ (2^6)^x=2^{2}, $$
  $$ 2^{6*x}=2^{2},$$
  $$6*x=2,$$
  $$x=\frac{2}{6}=\frac{1}{3}.$$
• Получили ответ:
  $$ log_{64}(4)=\frac{1}{3}.$$

Пример 4Вычислить логарифм от \(1\) по основанию \(8\): \(\quad log_{8}(1)=?\)

• Представим аргумент и основание в виде степени двойки. Напоминаю, что любое число в нулевой степени равно единице:
  $$ 8=2^3 \qquad 1=2^0;$$
  $$log_{8}(1)=log_{2^3}(2^0);$$
• В какую степень \(x\) надо возвести \(2^3\), чтобы получить \(2^{0}\):
  $$ (2^3)^x=2^{0}, $$
  $$ 2^{3*x}=2^{0},$$
  $$3*x=0,$$
  $$x=\frac{0}{3}=0.$$
• Получили ответ:
  $$ log_{8}(1)=0.$$

Пример 5Вычислить логарифм от \(15\) по основанию \(5\): \(\quad log_{5}(15)=?\)

Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 \qquad 15= ???;$$
\(15\) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$

Внимание!

Как понять, что некоторое число \(a\) не будет являться степенью другого числа \(b\)? Это довольно просто – нужно разложить \(a\) на простые множители.

\(16\) разложили, как произведение четырех двоек, значит \(16\) будет степенью двойки.

Разложив \(48\) на простые множители, видно, что у нас есть два множителя \(2\) и \(3\), значит \(48\) нельзя представить в виде степени какого-нибудь числа.

Преобразования логарифмических выражений

Для работы с логарифмическими выражениями надо знать несколько основных свойств логарифмов. Первое из них помогает вычислять логарифм произведения.

Для доказательства этого правила введем обозначения. Пусть

Тогда нам надо доказать, что z = x + у. По определению логарифма мы можем записать что

Теперь подставим (1) и (2) в (3):

Получили, что az = ax+y. В этом равенстве в обеих частях стоят степени с совпадающим основанием а. Значит, должны совпадать и их степени, то есть

что и мы и пытались доказать.

Убедимся в справедливости этого правила на простейшем примере. Очевидно, что

log₂ 4 = 2, ведь 22 = 4

log₂ 8 = 3, ведь 23 = 8

log₂ 32 = 5, ведь 25 = 32

С одной стороны, так как

2 + 3 = 5

то и

log₂ 4 + log₂ 8 = log₂ 32

С другой стороны, число 32 можно представить как произведение 4•8, то есть

log₂ 32 = log₂ (4•8)

С учетом этого получаем, что

log₂4 + log₂8 = log₂32 = log₂(4•8)

Покажем несколько примеров использования только что доказанного правила:

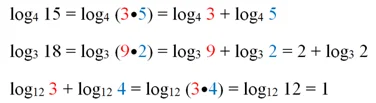
Отдельно отметить, что правило сложения логарифмов действует и в том случае, когда складываются не два, а большее количество логарифмов:

Второе правило используют для определения логарифма от степени какого-либо числа.

Грубо говоря, показатель степени можно перенести и записать перед знаком логарифма. Сначала для наглядности приведем доказательство только для случая, когда r– целая степень. Тогда число br можно представить как произведение r множителей, равных b. Однако логарифм такого произведения можно заменить на сумму r логарифмов:

Однако более строгое доказательство должно рассматривать и случай, когда r – это отрицательное или даже дробное число. Поэтому, как и в ситуации с доказательством первого правила, введем переменные. Пусть

Получается, что нам доказать, что у = r•x. Из определения логарифма следуют следующие формулы:

Подставляя первую формулу во вторую, получаем:

И снова, если у двух равных степеней равны основания, то и показатели обязательно будут равными:

Это равенство мы и пытались доказать.

Продемонстрируем, как работает это свойство логарифмов:

Правило работает и в обратную сторону:

Задание. Чему равна дробь

Третье правило помогает вычислять логарифм от частного или дроби.

Для доказательства этого свойства логарифмов воспользуемся уже доказанными нами двумя правилами. Но предварительно напомним, что произвольное число с в степени (– 1) представляет собой дробь 1/с:

Тогда доказательство будет записываться в две строчки:

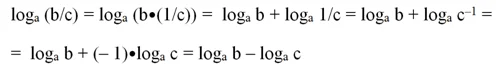
С помощью полученной формулы возможно выполнить следующие преобразования:

Заметим, что все полученные формулы справедливы только в том случае, когда под знаком логарифма стоят исключительно положительные числа. Например, вполне допустимо преобразование

но ошибочной будет такая запись:

ведь в левой части стоит выражение, имеющее смысл, а в правой – выражение, смысла не имеющее.

Но что делать в случае, если необходимо упростить выражение с переменными, которые могут принимать как положительные, так и отрицательные значения? Получается, что запись

не является корректной. Действительно, если и х, и у являются отрицательными числами, то их произведение ху положительно. Но тогда получается, что при некоторых значениях переменных левая часть равенства имеет смысл, а правая – нет. Это значит, что оно не является тождеством.

Здесь может помочь использование . Запись

уже будет корректной при любых допустимых значениях х и у. Если же хоть одна из переменных будет равна нулю, то обе части равенства одновременно потеряют смысл. Таким образом, данное равенство можно считать тождеством.

Аналогично и формулу разности логарифмов можно представить в более общем случае, при котором допускаются отрицательные значения переменных:

Можно ли записать равенство log_aх2 = 2log_aх, если допускается, что х может быть и отрицательным? Нет, нельзя, ведь при отрицательных х выражение левая часть равенства будет иметь смысл, а правая нет. Однако использование модуля поможет и в этом случае. Можно написать, что

Аналогичным образом можно упростить и любые другие логарифмы, аргументы которых возведены в четную степень:

Ещё раз уточним, что эти правила используются при упрощении выражений с переменными, если те могут принимать отрицательные значения. Если же известно, что числа b и c положительны, то лучше использовать формулы, не содержащие модулей.

Практическое применение

Являясь исключительно математическим инструментом, кажется далёким от реальной жизни, что логарифм неожиданно приобрёл большое значение для описания объектов реального мира. Трудно найти науку, где его не применяют. Это в полной мере относится не только к естественным, но и гуманитарным областям знаний.

Логарифмические зависимости

Приведём несколько примеров числовых зависимостей:

• Число простых чисел на интервале от 1 до n приблизительно равно n / ln (n).
• Для поиска k-го простого числа можно пользоваться формулой k * ln (k).
• Логарифмическое распределение часто используется для оценки вероятностных событий в генетике и физике.
• В информатике известно, что для хранения в памяти компьютера натурального числа N потребуется log 2(N) + 1 бит памяти.

Механика и физика

Исторически механика и физика всегда развивались с использованием математических методов исследования и одновременно служили стимулом для развития математики, в том числе логарифмов. Теория большинства законов физики написана языком математики. Приведём только два примера описания физических законов с использованием логарифма.

Решать задачу расчёта такой сложной величины как скорость ракеты можно, применяя формулу Циолковского, которая положила начало теории освоения космоса:

V = I * ln (M1/M2), где

• V – конечная скорость летательного аппарата.
• I – удельный импульс двигателя.
• M 1 – начальная масса ракеты.
• M 2 – конечная масса.

Другой важный пример — это использование в формуле другого великого учёного Макса Планка, которая служит для оценки равновесного состояния в термодинамике.

S = k * ln (Ω), где

• S – термодинамическое свойство.
• k – постоянная Больцмана.
• Ω – статистический вес разных состояний.

Химия

Менее очевидным будет использования формул в химии, содержащих отношение логарифмов. Приведём тоже только два примера:

• Уравнение Нернста, условие окислительно-восстановительного потенциала среды по отношению к активности веществ и константой равновесия.
• Расчёт таких констант, как показатель автопролиза и кислотность раствора тоже не обходятся без нашей функции.

Психология и биология

И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.

После вышеприведённых примеров уже не удивляет, что и в биологии широко используется тема логарифмов. Про биологические формы, соответствующие логарифмическим спиралям, можно писать целые тома.

Другие области

Кажется, невозможно существование мира без связи с этой функцией, и она правит всеми законами. Особенно, когда законы природы связаны с геометрической прогрессией. Стоит обратиться к сайту МатПрофи, и таких примеров найдётся множество в следующих сферах деятельности:

• Теории акустики.
• Радиотехнике и электросвязи.
• Астрономии.
• Сейсмологии.
• Оптике.
• Фотографии.
• Сельском хозяйстве.
• Теории управления.

Список может быть бесконечным. Освоив основные закономерности этой функции, можно окунуться в мир бесконечной мудрости.

Интересные сведения

Логарифмы (особенно натуральные и десятичные) широко применимы почти во всех сферах деятельности.

Например, в теории простых чисел, количество простых чисел в интервале от 0 до n будет равно приблизительно: 

В математическом анализе, как мы уже убедились ранее, натуральные логарифмы встречаются сплошь и рядом, при этом они объединяют тригонометрические и логарифмические функции при помощи интегралов, например интеграл от тангенса:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти натуральное число N понадобится

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

https://youtube.com/watch?v=e_MZrekT1-0

Доказательство основного свойства натурального логарифма

Таблица десятичных логарифмов

х»заказ данных=»x«стиль = «минимальная ширина: 9,2857%; ширина:9,2857%;»>х	х «заказ данных = «lg x«стиль = «минимальная ширина: 15,4762%; ширина:15,4762%;»>lg x	х»заказ данных=»x«стиль = «минимальная ширина: 9,5238%; ширина:9,5238%;»>х	х «заказ данных = «lg x«стиль = «минимальная ширина: 16,9048%; ширина:16,9048%;»>lg x	х»заказ данных=»x«стиль = «минимальная ширина: 9,0476%»; ширина:9,0476%;»>х	х «заказ данных = «lg x«стиль = «минимальная ширина: 14,7619%; ширина:14,7619%;»>lg x	х»заказ данных=»x«стиль = «минимальная ширина: 9,7619%»; ширина:9,7619%;»>х	х «заказ данных = «lg x«стиль = «минимальная ширина: 15,2381%; ширина:15,2381%;»>lg x
1	26	1.41497	51	1.70757	76	1.88081
2	0,30103	27	1.43136	52	1716	77	1,88649
3	0,47712	28	1.44716	53	1.72428	78	1.89209
4	0,60206	29	1,4624	54	1.73239	79	1,89763
5	0,69897	тридцать	1.47712	55	1.74036	80	1.90309
6	0,77815	31	1.49136	56	1.74819	81	1.90849
7	0,8451	32	1.50515	57	1,75587	82	1.91381
8	0,90309	33	1.51851	58	1,76343	83	1.91908
9	0,95424	34	1.53148	59	1.77085	84	1.92428
10	1	35	1.54407	60	1.77815	85	1.92942
одиннадцать	1.04139	36	1,5563	61	1,78533	86	1,9345
12	1.07918	37	1,5682	62	1.79239	87	1.93952
1. 3	1.11394	38	1,57978	63	1,79934	88	1,94448
14	1.14613	39	1.59106	64	1.80618	89	1,94939
15	1.17609	40	1.60206	65	1.81291	90	1,95424
16	1.20412	41	1,61278	66	1.81954	91	1.95904
17	1.23045	42	1.62325	67	1.82607	92	1,96379
18	1.25527	43	1,63347	68	1.83251	93	1,96848
19	1,27875	44	1,64345	69	1,83885	94	1,97313
20	1.30103	45	1.65321	70	1,8451	95	1,97772
21	1.32222	46	1,66276	71	1,85126	96	1,98227
22	1.34242	47	1,6721	72	1,85733	97	1,98677
23	1.36173	48	1,68124	73	1,86332	98	1,99123
24	1.38021	49	1,6902	74	1,86923	99	1,99564
25	1.39794	50	1,69897	75	1.87506	100	2

microexcel.ru

х «заказ данных = «lg x«стиль = «минимальная ширина: 12,2449%»; ширина:12,2449%;»>lg x	1	2	3	4	5	6	7	8	9	10
х»заказ данных=»x»>х	10	102	103	104	105	106	107	108	109	1010

Исторический очерк[]

Вещественный логарифм

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′. Термин логарифм, предложенный Непером, утвердился в науке.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:

LogNap⁡(x)=M∗(ln⁡(M)−ln⁡(x)){\displaystyle \operatorname {LogNap} (x)=M*(\ln(M)-\ln(x))}

Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.

Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.

Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» () Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.

Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Комплексный логарифм

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.

Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.