Основные свойства логарифмов

Десятичные и натуральные логарифмы

Логарифм числа x по основанию 10 называется логарифмом по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все приведенные выше формулы остаются актуальными и для десятичных логарифмов. Например,

lg(xy)=lgx+lgy(x>0,y>0).

Натуральный логарифм числа х (обозначение lnx) — это логарифм числа х по основанию е. Число е иррационально, примерно равно 2,71. Например, ln e = 1. С помощью формулы (8) любой логарифм можно привести к десятичному или натуральному логарифму:

logab=lgblga=lnblna(a>0,a≠1,b>0)

Что такое логарифм степени числа и как его посчитать

Логарифм по основанию а от b представляет собой число t, демонстрирующее степень, в которую требуется возвести а для получения в результате b:

\(\Large{{\log_a{b}=t\quad\Leftrightarrow\quad a^t=b }}\)

Здесь a>0, b отлично от нуля и является положительным.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

По той причине, что степень может иметь любое значение без какого-либо предела, имеем:

\(t\in \mathbb{R}\)

В результате получается вывести главное логарифмическое тождество.

Основное логарифмическое тождество является соотношением, записанным в виде:

\(\Large{a^{\log_ab}=b}\)

Исходя из рассмотренных закономерностей, справедливы следующие соотношения:

\({\large{\begin{array}{|ll|l|} \hline \qquad \qquad \qquad \qquad {\small{\text{Формулы}}} && \qquad \qquad{\small{\text{Ограничения}}}\\ &&\\ \hline \textbf{(1)} \log_a1=0&&a>0, a\ne 1\\ &&\\ \textbf{(2)} \log_aa=1 &&a>0, a\ne 1\\ &&\\ \textbf{(3)} \log_{a}{b^m}=m\log_a|b|&(m — {\small{\text{четн.}}})&a>0, a\ne 1, b\ne 0\\ &&\\ \textbf{(4)}\log_{a}{b^m}=m\log_ab& (m — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(5)} \log_{a^n}{b}=\frac 1n\log_{|a|}b&(n — {\small{\text{четн.}}})&a\ne 0, a\ne 1, b>0\\ &&\\ \textbf{(6)}\log_{a^n}b=\frac1n\log_ab&(n — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(7)} \log_a{bc}=\log_a|b|+\log_a|c|&&a>0, a\ne 1, bc\ne 0\\ &&\\ \textbf{(8)} \log_a{\dfrac bc}=\log_a|b|-\log_a|c|&&a>0, a\ne 1,bc\ne 0 \\ &&\\ \textbf{(9)} a^{\log_ab}=b &&a>0, a\ne 1, b>0\\ &&\\ \textbf{(10)}c^{\log_ab}=b^{\log_ac}&&a>0, a\ne 1, b>0, c>0\\ &&\\ \textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ \textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ &&\\ {\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\ \textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \hline \end{array}}}\)

Если все условия, связанные с ограничениями, выполняются, то эти формулы справедливы в прямом и обратном направлениях.

Логарифм степени какого-либо числа представляет собой результат умножения логарифма модуля основания данной степени и показателя этой степени:

\(\log_{a}x^r=r \cdot \log_{a}⁡|x|\)

В данном случае \(x^r,a > 0\), \(a \ne 1\).

Разберем наглядный пример такой взаимосвязи. Предположим, что имеется некое выражение, значение которого требуется определить:

\(\log_{5}⁡\frac{1}{125}+\log_{11}⁡121\)

Рассмотрим выражение, записанное под знаком логарифма, и решим, что с ним делать. Заметим, что его можно переписать как основание логарифма в степени. Воспользуемся свойством логарифма степени, изученным ранее, и выполним преобразования:

\(log_{5}\frac{1}{125}+\log_{11}⁡121=\log_{5}5^{-3}+\log_{11}11^2=-3\log_{5}⁡5+2\log_{11}⁡11\)

Известно, что:

\(\log_{a}⁡a=1\)

Доведем вычисления до конца:

\(log_{5}\frac{1}{125}+\log_{11}⁡121=\log_{5}5^{-3}+\log_{11}11^2=-3\log_{5}⁡5+2\log_{11}⁡11=-3+2=-1\)

Ответ: \(\log_{5} \frac{1}{125}+\log_{11}⁡121=-1.\)

В процессе решения задач в разных главах разделов тригонометрии может потребоваться обратный перевод определения логарифма степени числа. Заметим, что оно также является справедливым.

Коэффициент, записанный перед знаком логарифма, допустимо заносить в степень выражения, находящегося под знаком логарифма:

\(s \log_{a}⁡x=\log_{a}x^s\)

Здесь a и b > 0, a≠1.

Рассмотрим наглядный пример. Пусть дано выражение, которое требуется упростить:

\(6 \log_{13}x^2-\log_{13}x^7\)

Воспользуемся логарифмическим свойством, чтобы записать степень за знаком логарифма:

\(6 \log_{13}x^2-\log_{13}x^7=6 \cdot 2 \log_{13}⁡x-7 \log_{13}⁡x=12 \log_{13}⁡x-7 \log_{13}⁡x=5 \log_{13}⁡x\)

Если под логарифмический знак записать коэффициент в виде числа 5, то получим:

\(6 \log_{13}x^2-\log_{13}x^7=6 \cdot 2 \log_{13}⁡x-7 \log_{13}⁡x=12 \log_{13}⁡x-7 \log_{13}⁡x=5 \log_{13}⁡x=\log_{13}x^5.\)

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

1. log a

   a

   = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a

   от самого этого основания равен единице.

2. log a

   1 = 0 — это логарифмический ноль. Основание a

   может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a

   0 = 1 — это прямое следствие из определения.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Логарифмом числа N


по основаниюа

называется показатель степених

,
в которую нужно возвестиа

,
чтобы получить числоN

При условии, что
,,

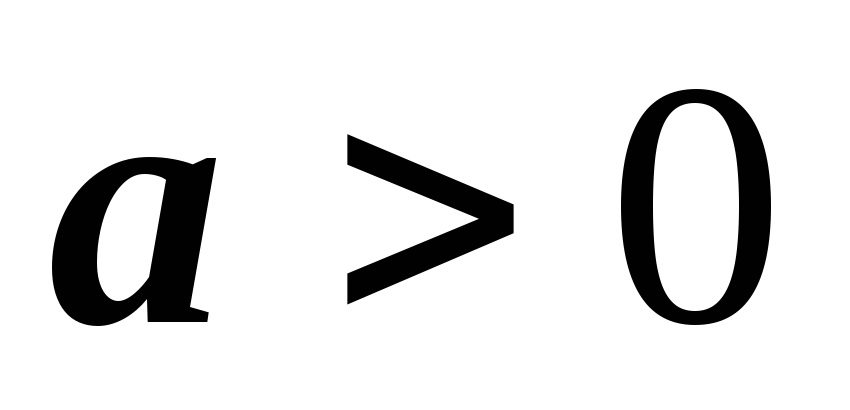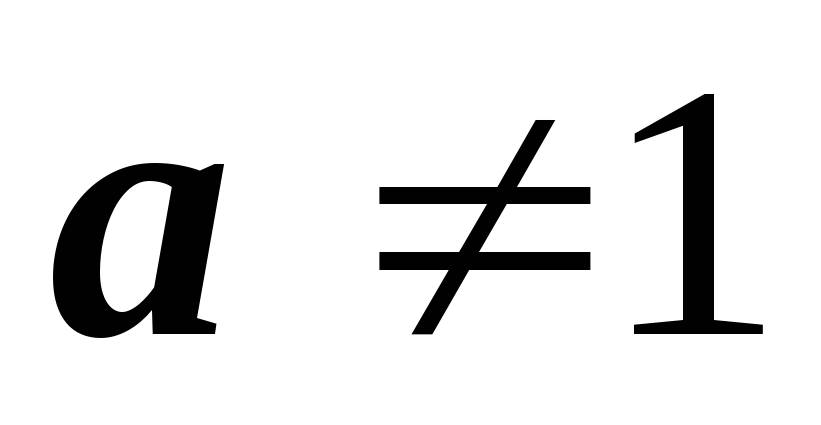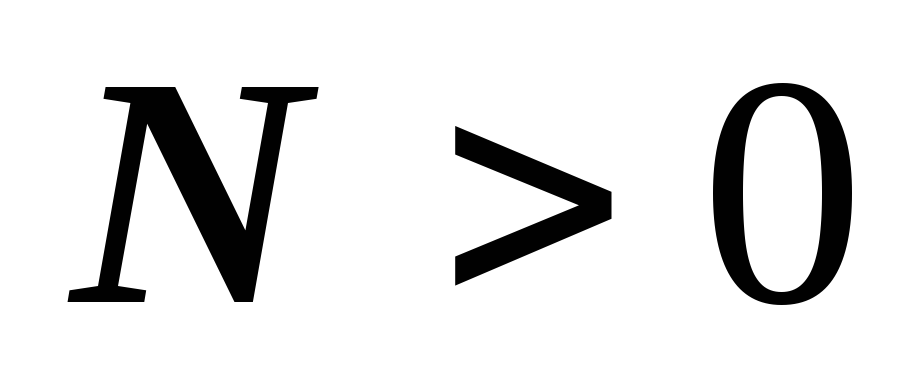
Из определения логарифма
следует, что
,
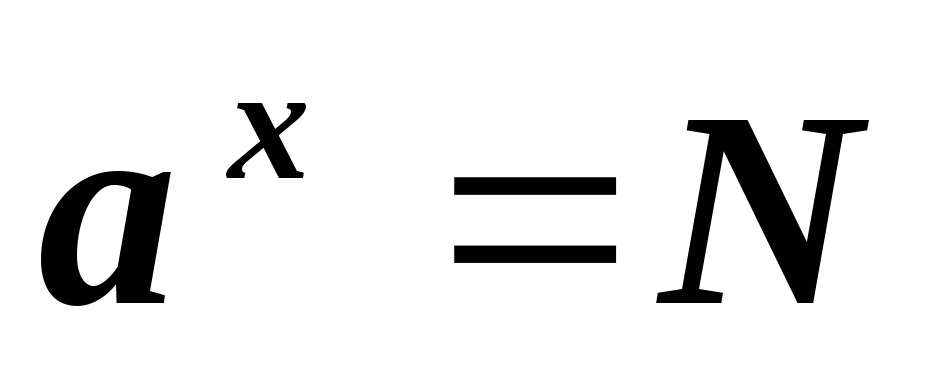т.е.

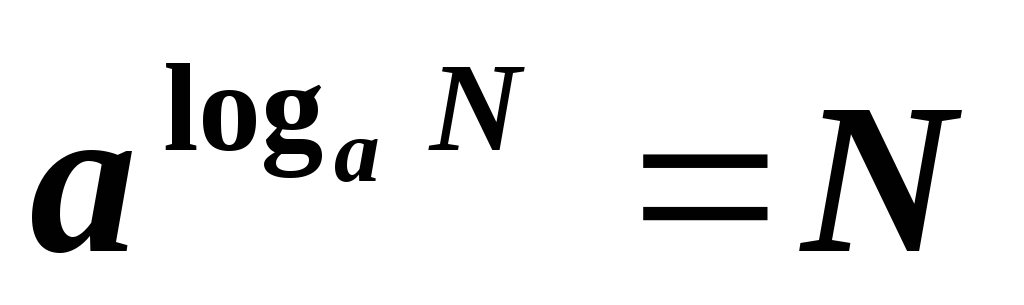
— это равенство является основным
логарифмическим тождеством.

Логарифмы по основанию 10
называются десятичными логарифмами.
Вместо
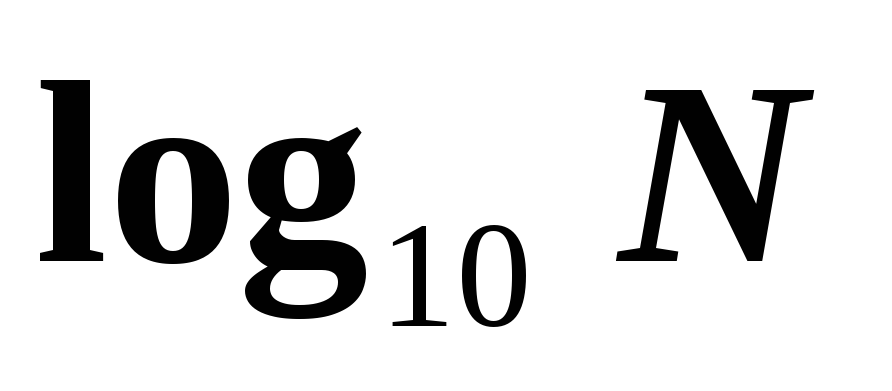пишут.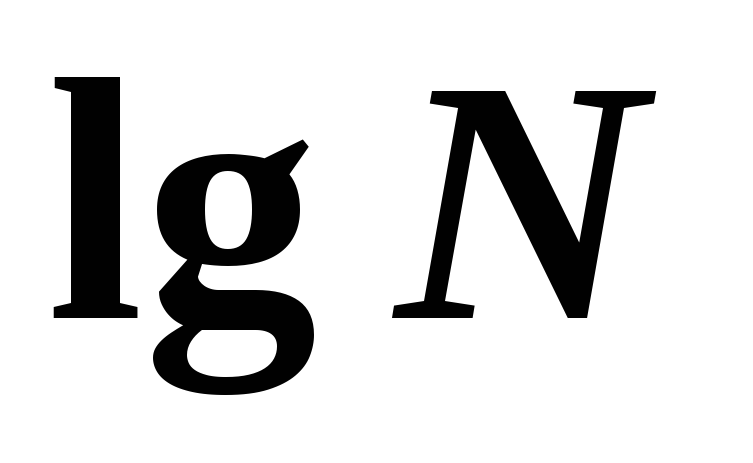

Логарифмы по основанию e


называются натуральными и обозначаются.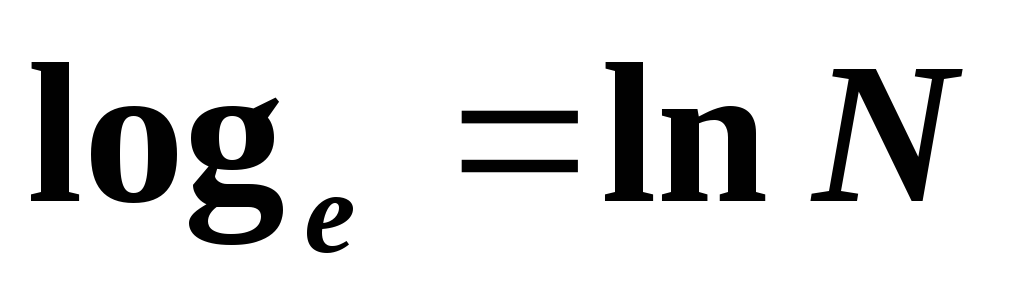

Основные свойства логарифмов.

Логарифм единицы
при любом основании равен нулю

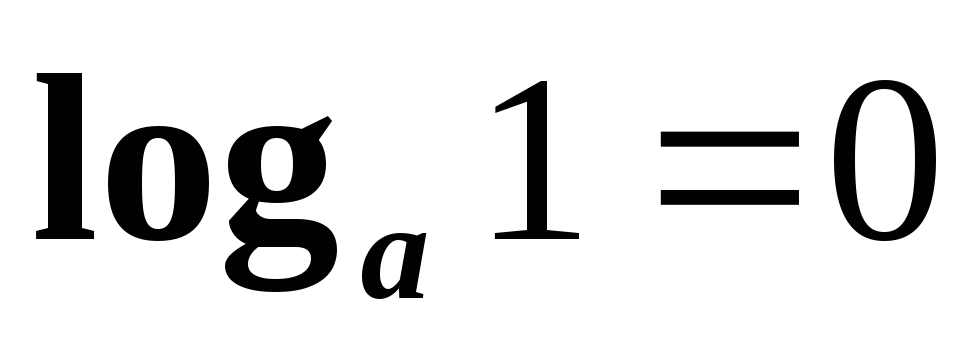
Логарифм
произведения равен сумме логарифмов
сомножителей.

3)
Логарифм частного равен разности
логарифмов

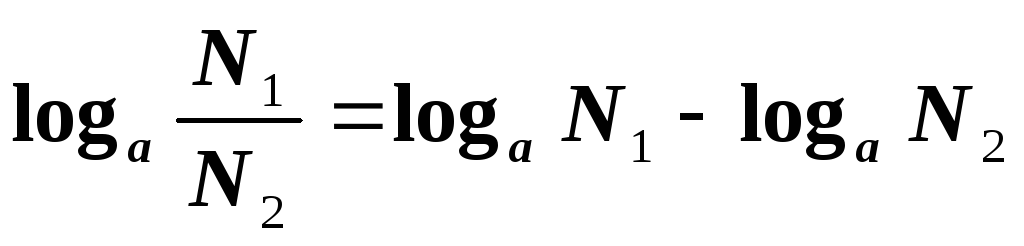
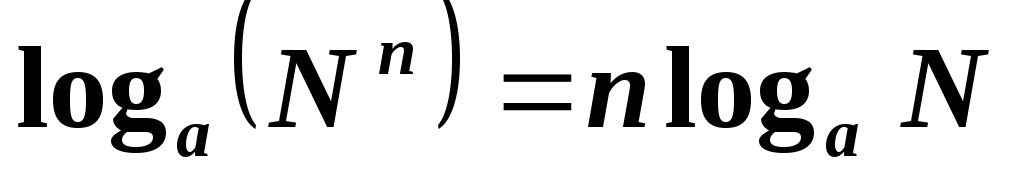
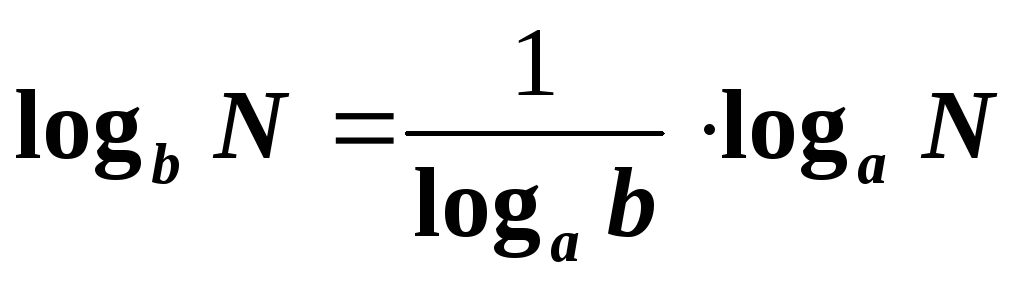
Множитель
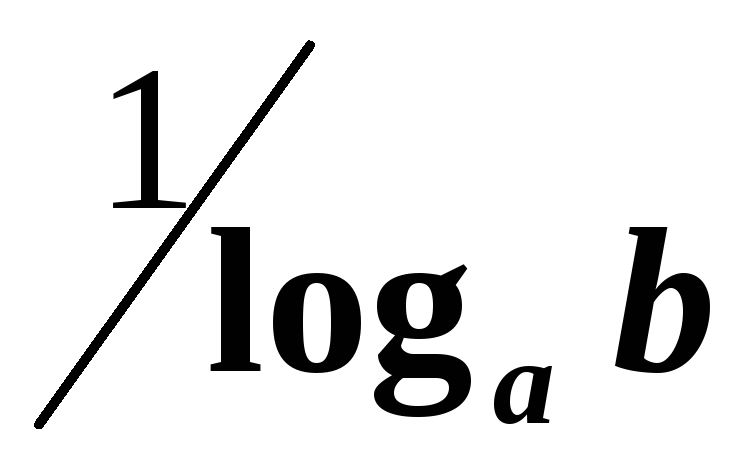называется модулем перехода от логарифмов
при основанииa

к логарифмам при основанииb

.

С помощью
свойств 2-5 часто удается свести логарифм
сложного выражения к результату простых
арифметических действий над логарифмами.

Например,

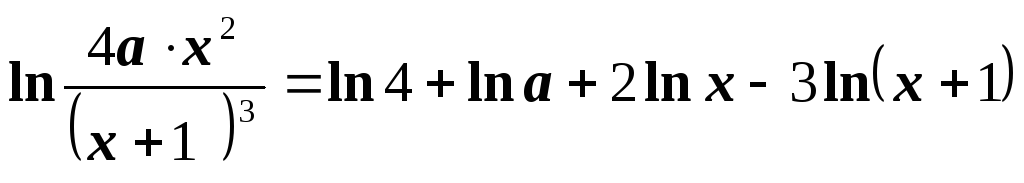
Такие
преобразования логарифма называются
логарифмированием. Преобразования
обратные логарифмированию называются
потенцированием.

Вычисление логарифма равносильно решению показательного уравнения

Экспоненциальное уравнение:

топор=б,

при а > 0 а ≠ 1; б > 0, где

х — показатель степени, а — основание степени, b — степень числа а.

Логарифмическое уравнение:

журнал б = х,

при а > 0 а ≠ 1; б > 0, где

х — логарифм числа b по основанию а, а — основание логарифма, b — число под знаком логарифма.

Примеры:

25 = 32 ⇔ 5 = log2 32

34 = 81 ⇔ 4 = log3 81

log1/5 125 = -3 ⇔ (1/5)-3 = 125

log2116 = -4 ⇔ 2-4 = 116.

Пример 1

Найти логарифм: log 4 8

Введите log4 8 через x:

log4 8 = х

Перейдем к показательному уравнению:

4х = 8

Приводим показательное уравнение к основанию 2 и решаем его:

22х = 23

2х=3

х=32

Отвечать:

log48 = 32

Пример 2

Найдите x, если: logx 125 = 32

За определением логарифма мы имеем:

х3/2 = 125

Возведем обе части в степень 23, используя свойства степеней:

(х3/2)2/3 = 1252/3

х = (53)2/3 = 53 2/3 = 52 = 25

Отвечать:

х=25

Логарифм — свойства, формулы, график

Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Определение логарифма ⇓Графики логарифма ⇓Свойства логарифма ⇓   Область определения, множество значений, возрастание, убывание ⇓   Частные значения ⇓   Основные формулы логарифмов ⇓      Основное свойство логарифмов и его следствия ⇓      Формула замены основания ⇓   Доказательство основных формул логарифмов ⇓Обратная функция ⇓Производная логарифма ⇓Интеграл ⇓Выражения через комплексные числа ⇓Разложение в степенной ряд ⇓

См. также:

Показательная функция, ее график, свойства, формулы Натуральный логарифм, функция ln x

Логарифм с основанием a – это функция  y(x) = loga x, обратная к показательной функции с основанием a:   x(y) = a y.

В дальнейшем будем считать, что основание логарифма a положительное, не равное единице число: .

Десятичный логарифм – это логарифм по основанию числа 10:   lg x ≡ log10 x. Натуральный логарифм – это логарифм по основанию числа e:   ln x ≡ loge x.

2,718281828459045…; .

Графики логарифма

Графики логарифма y = loga x при различных значениях основания a.

График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0

Область определения, множество значений, возрастание, убывание

Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.

Область определения
Область значений	– ∞	– ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	x = 1	x = 1
Точки пересечения с осью ординат, x = 0	нет	нет
+ ∞	– ∞
– ∞	+ ∞

Частные значения

Логарифм по основанию 10 называется десятичным логарифмом и обозначается так: Логарифм по основанию e называется натуральным логарифмом:

Формула замены основания

Логарифмирование – это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.

Потенцирование – это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование.

При этом суммы членов преобразуются в произведения сомножителей.

Доказательство основных формул логарифмов

• Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
• Рассмотрим свойство показательной функции . Тогда
• .

Применим свойство показательной функции .

Докажем формулу замены основания. ; . Полагая c = b, имеем:

Производная логарифма

Производная логарифма от модуля x: . Производная n-го порядка:

Вывод формул > > >

Для нахождения производной логарифма, его нужно привести к основанию e. ; .

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z: . Выразим комплексное число z через модуль r и аргумент φ: . Тогда, используя свойства логарифма, имеем:

Или Однако, аргумент φ определен не однозначно. Если положить , где n — целое, то будет одним и тем же числом при различных n.

Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература: И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Логарифм. Свойства логарифмов

Логарифм. Свойства логарифмов

Рассмотрим равенство . Пусть нам известны значения  и и мы хотим найти значение .

То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

Пусть переменная  может принимать любое действительное значение, тогда на переменные  и накладываются такие ограничения: ,  ,  

Если нам известны значения  и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое  действие, которое называется логарифмирование.

Чтобы найти значение , мы берем логарифм числа  по основанию :

Итак,

Логарифмом числа  по основанию  называется показатель степени, в которую надо возвести  , чтобы получить .

То есть основное логарифмическое тождество:

            ,  ,  

является по сути математической записью определения логарифма.

Математическая операция  логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

Перечислим основные свойства логарифмов:

(,  ,   ,  ,  

1. 

2. 

3. 

4. 

5. 

Следующая группа свойств позволяет представить  показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента  перед знаком логарифма:

6. 

7. 

8. 

9. 

Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию:

10. 

11. 

12. (следствие из свойства 11)

Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

13. 

14. 

15. 

Частные случаи:

— десятичный логарифм

 —  натуральный логарифм

При упрощении выражений, содержащих логарифмы  применяется общий подход:

1. Представляем десятичные дроби в виде обыкновенных.

2. Смешанные числа представляем в виде неправильных дробей.

3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.

4. Стараемся привести все логарифмы к одному основанию.

5. Применяем свойства логарифмов.

Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.

Пример 1.

Вычислить:

Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.

==(по свойству 7)=(по свойству 6) =

Подставим показатели, которые у нас получились в исходное выражение. Получим:

Ответ: 5,25

Пример 2. Вычислить:

Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

Разложим числа, стоящие под знаком логарифма на простые множители:

Применим свойства 4 и 6:

Введем замену  

Получим:

Ответ:  1 

Скачать таблицу логарифм и его свойства

И.В. Фельдман, репетитор по математике.

Глава 2. Элементы высшей математики.

1. Пределы

Пределом функции

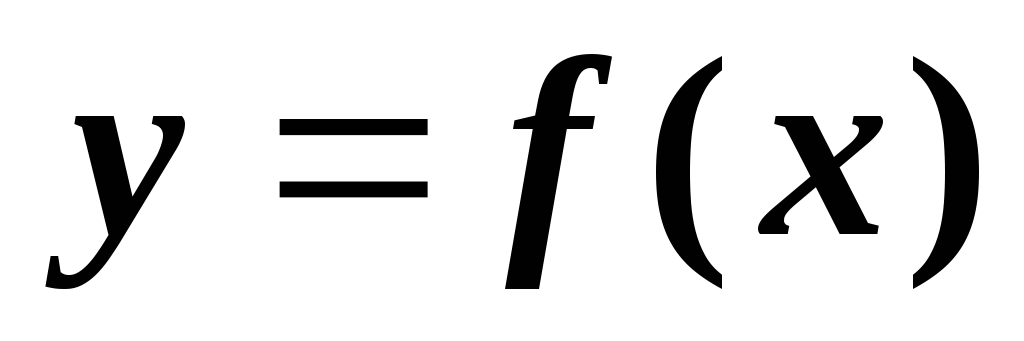
является конечное число А, если при
стремлении xx

для каждого наперед заданного
,
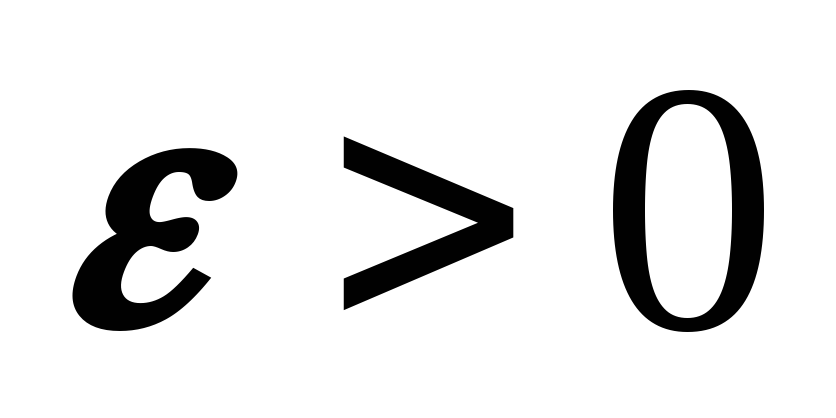найдется такое число
,
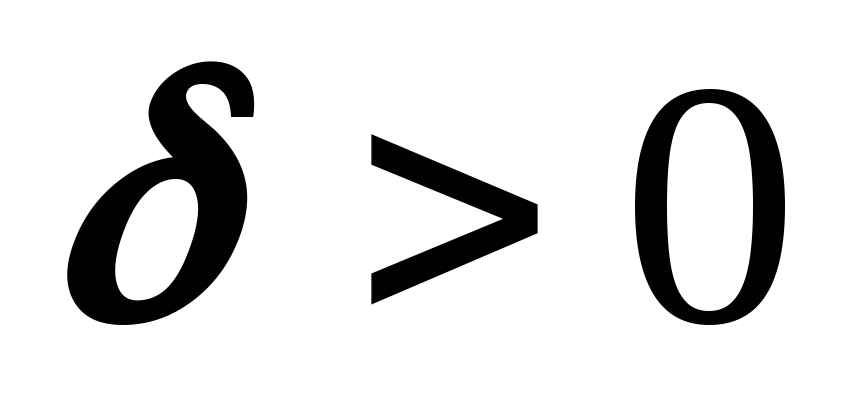что как только
,
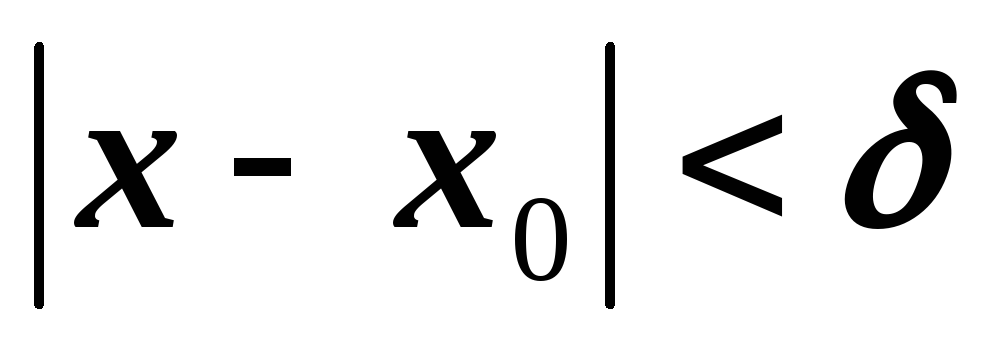то
.

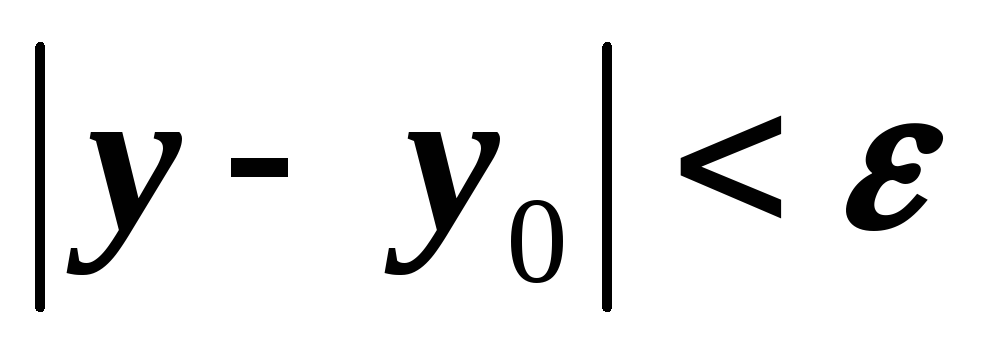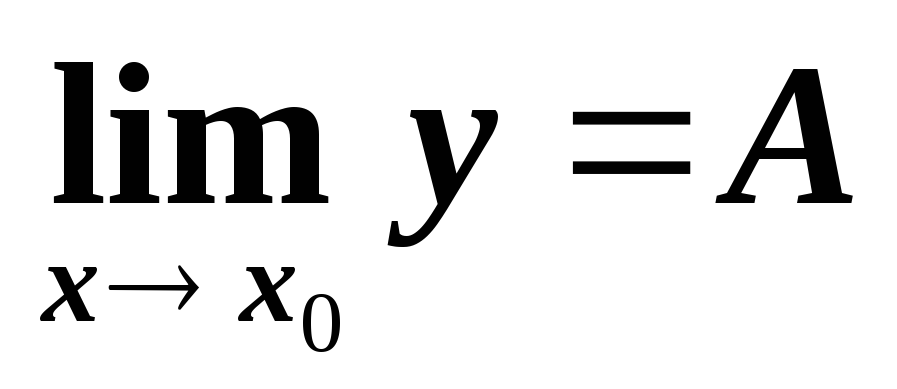
Функция, имеющая предел, отличается от
него на бесконечно малую величину:
,
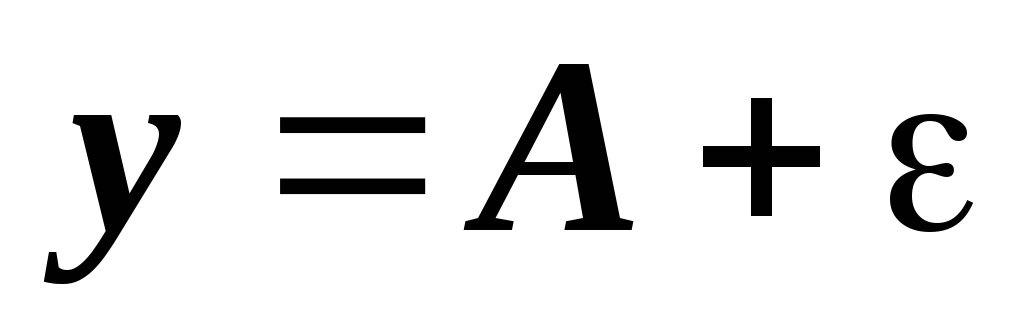где- б.м.в., т.е..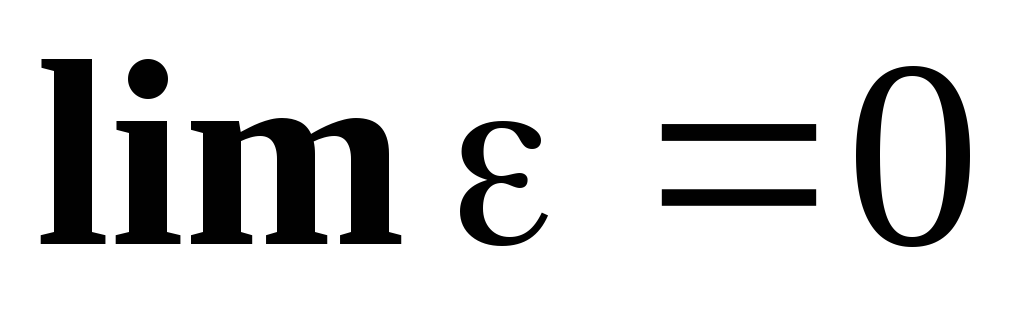

Пример. Рассмотрим функцию
.

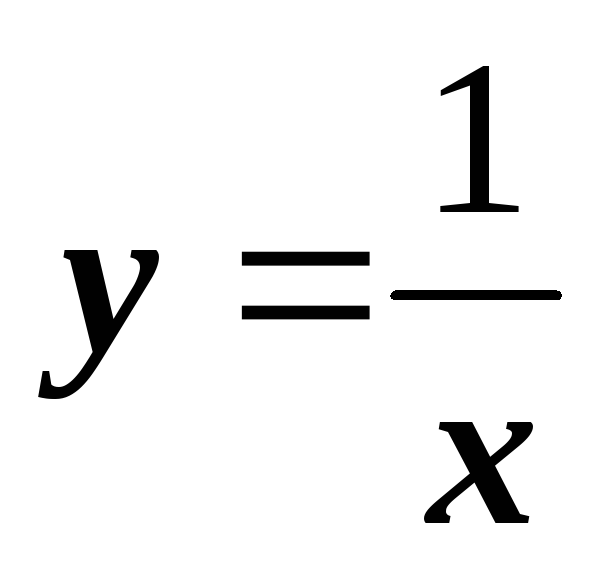При стремлении
,
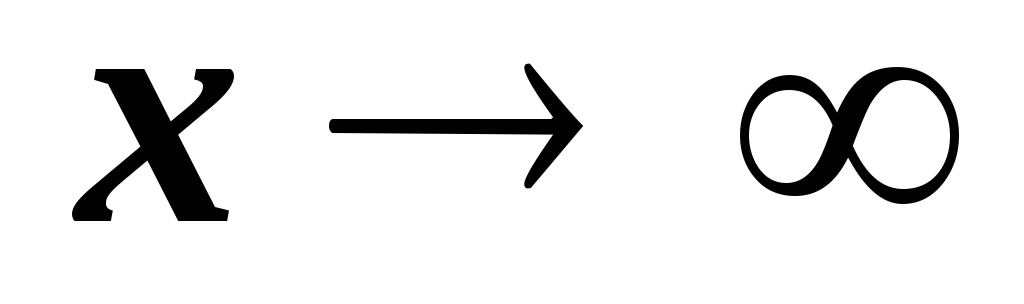функцияy


стремится к нулю:

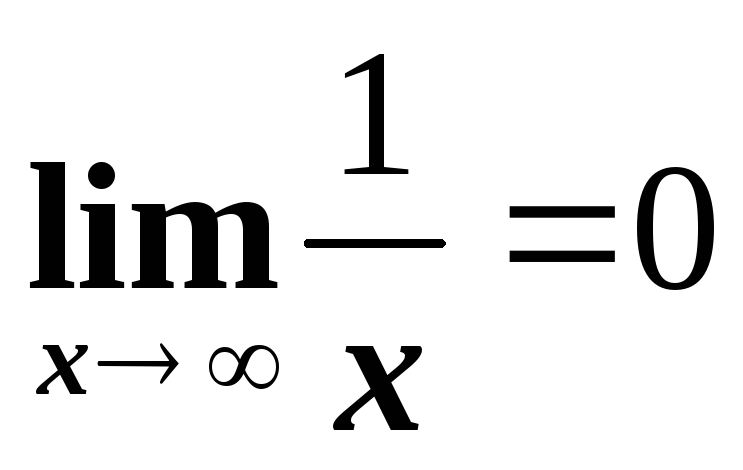
1.1. Основные теоремы о пределах.

Предел
постоянной величины равен этой постоянной
величине

.

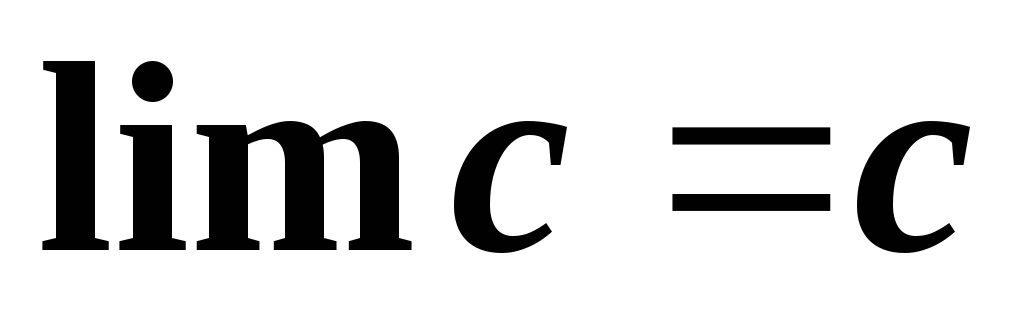Предел
суммы (разности) конечного числа функций
равен сумме (разности) пределов этих
функций.

Предел
произведения конечного числа функций
равен произведению пределов этих
функций.

Предел
частного двух функций равен частному
пределов этих функций, если предел
знаменателя не равен нулю.

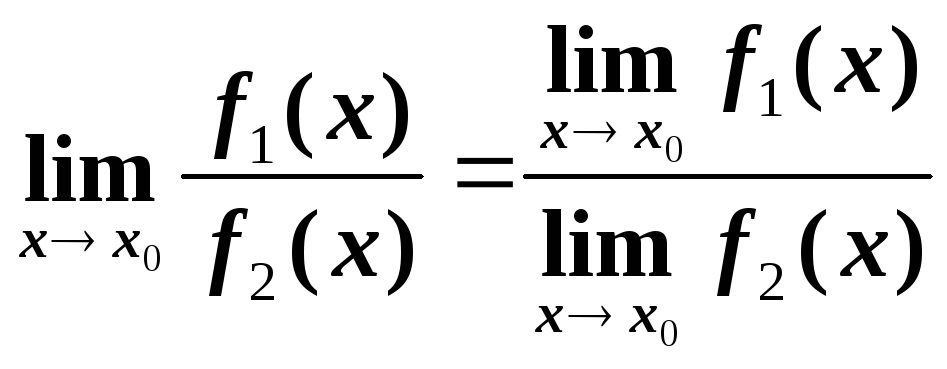
Замечательные пределы

,
,
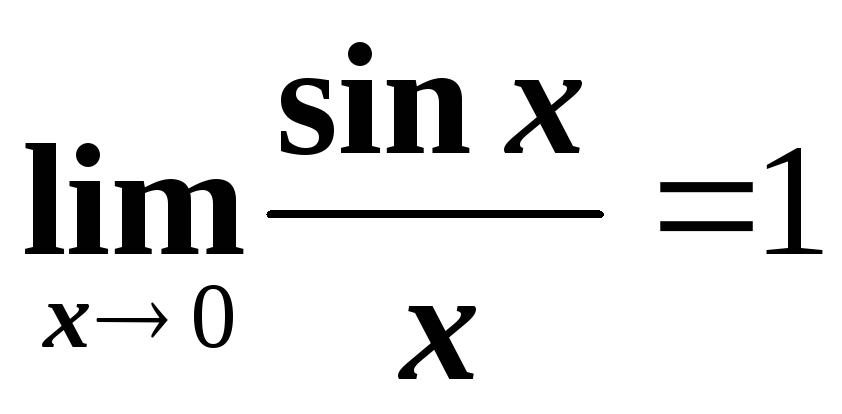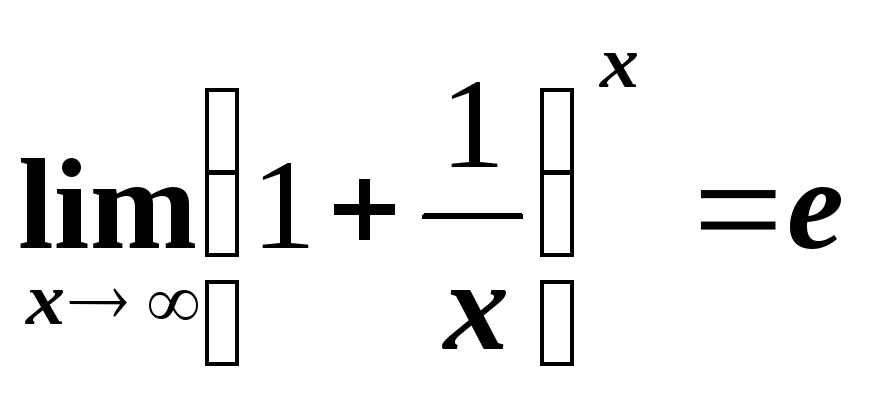где

1.2. Примеры вычисления пределов

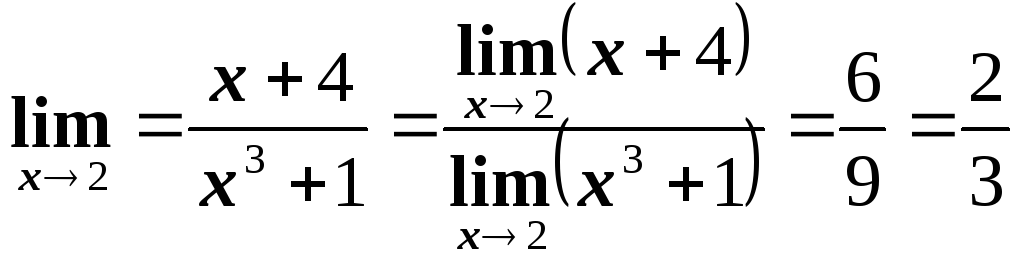
Однако, не все пределы вычисляются так
просто. Чаще вычисление предела сводится
к раскрытию неопределенности типа:

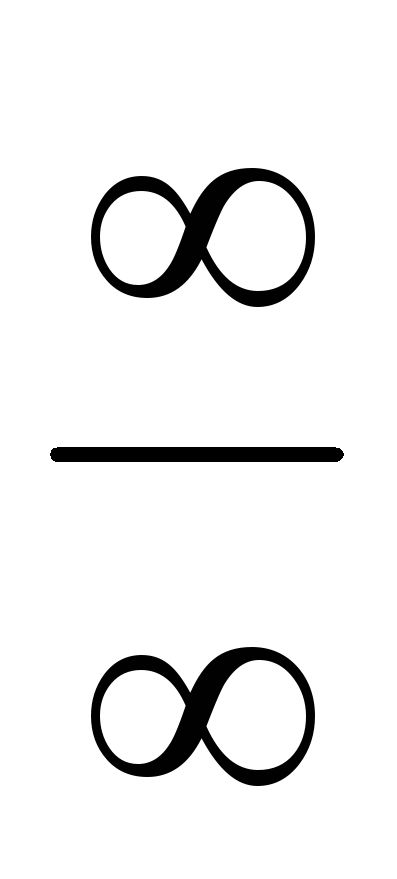
или
.

.

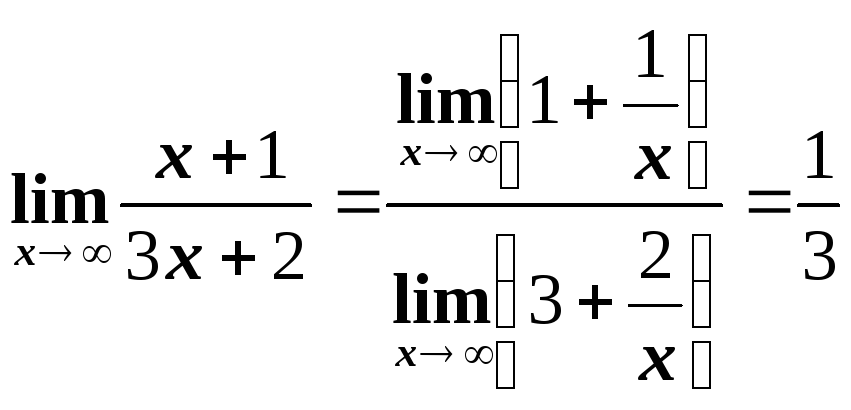2. Производная функции

Пусть мы имеем функцию
,
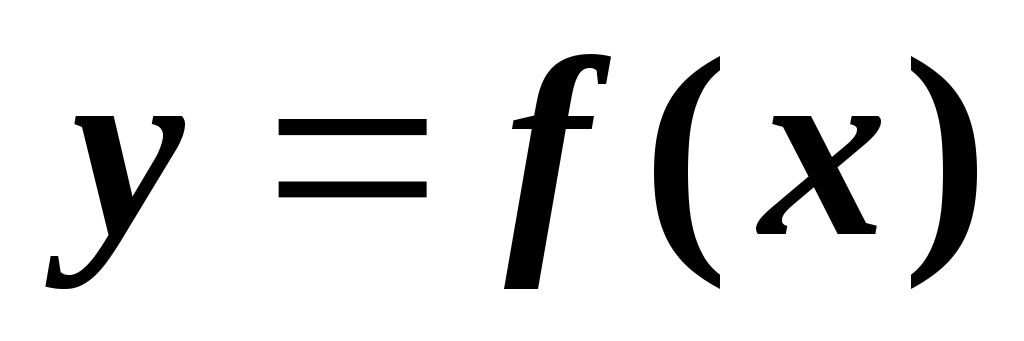непрерывную на отрезке
.

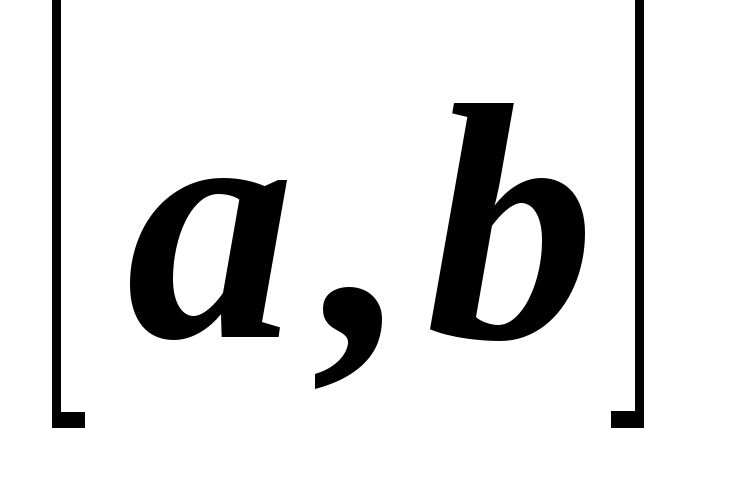Аргумент
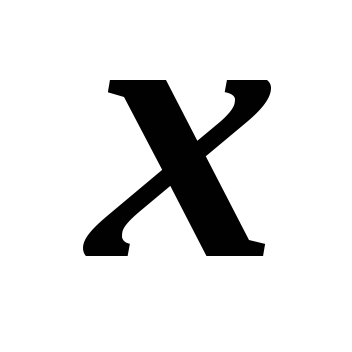получил некоторое приращение
.
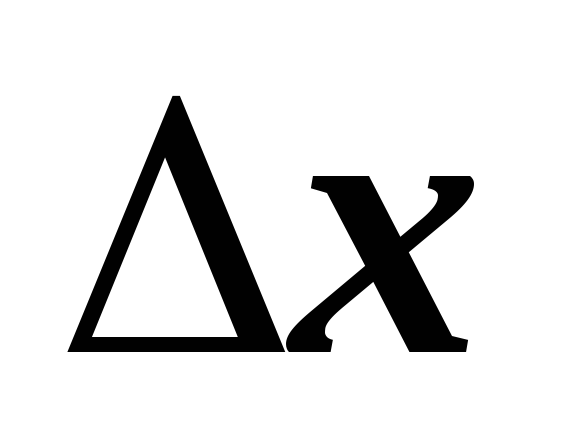Тогда и функция получит приращение
.

Значению аргумента

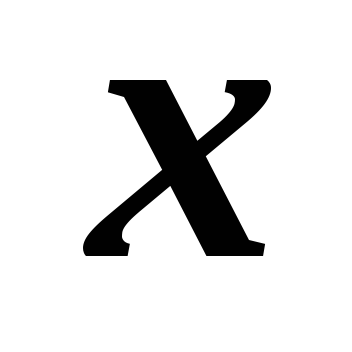
соответствует значение функции
.

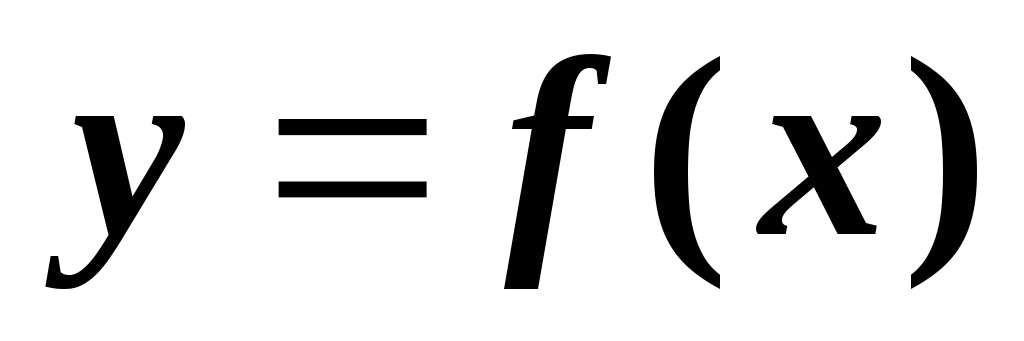Значению аргумента
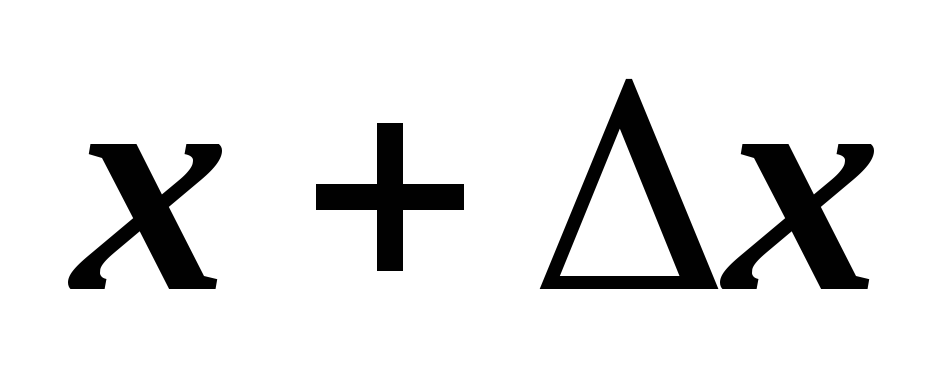соответствует значение функции
.

Следовательно,
.

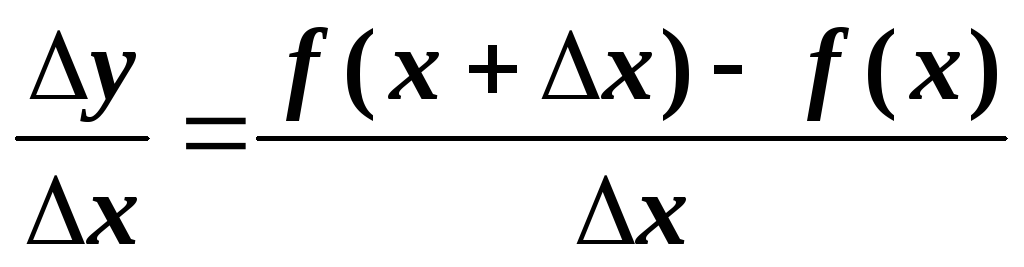
Найдем предел этого отношения при
.
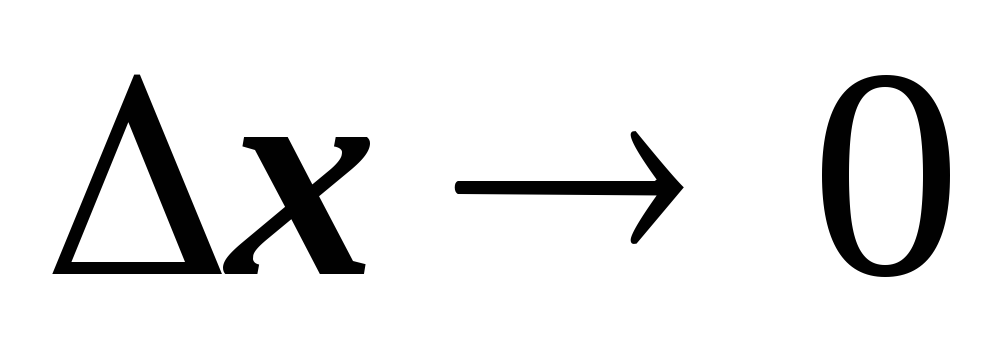Если этот предел существует, то он
называется производной данной функции.

Определение 3Производной данной функции
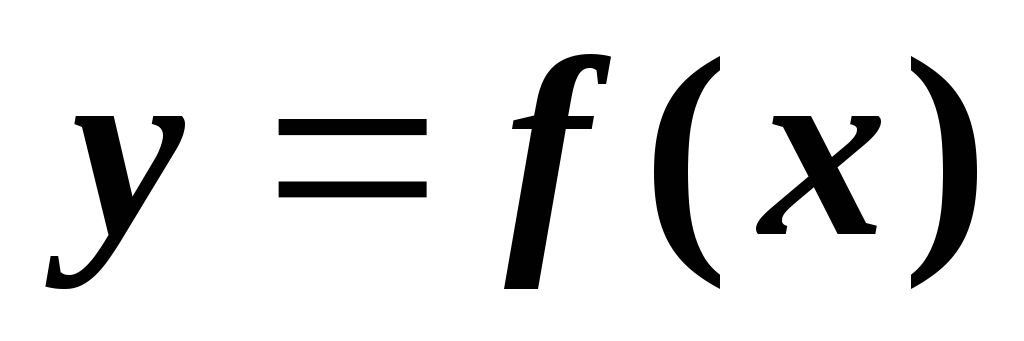по
аргументу
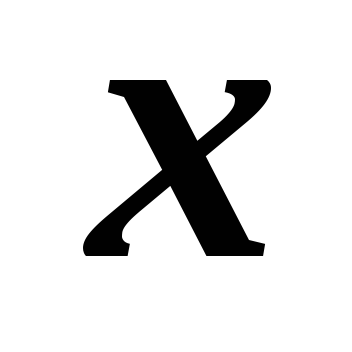называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.

Производная функции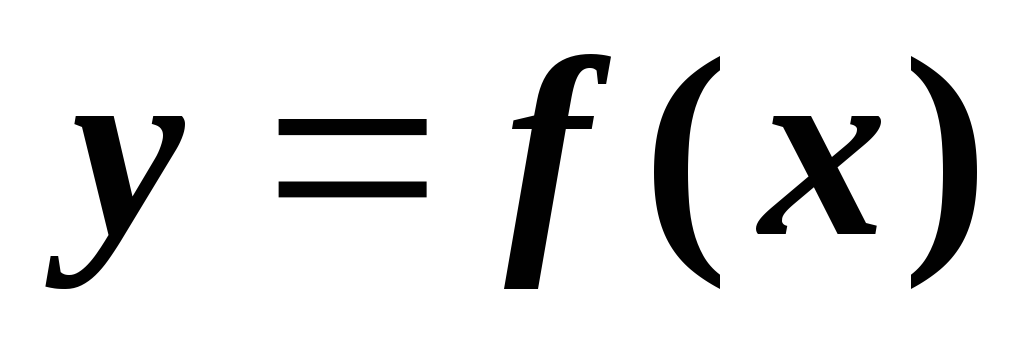может быть обозначена следующим образом:

;
;
;
.

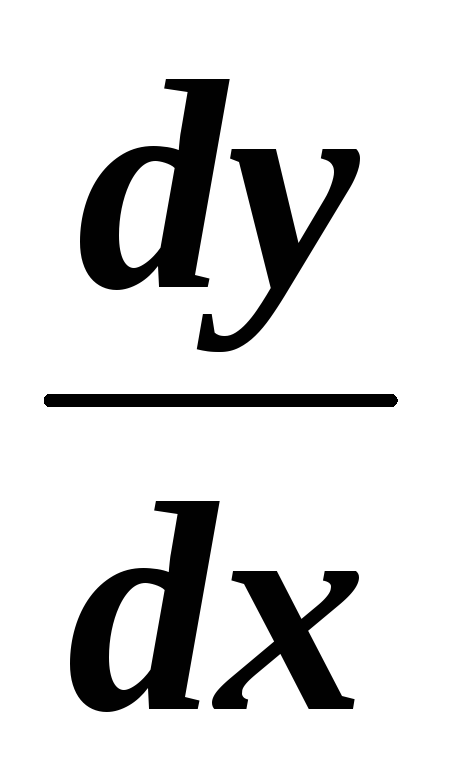Определение 4Операция нахождения производной от
функции называетсядифференцированием.

Замена переменной в уравнениях с логарифмами

Разберем еще один частый тип логарифмических уравнений — это уравнения с заменой переменной. Общий принцип заключается в том, чтобы привести все логарифмы в уравнении к одинаковому основанию и одинаковому аргументу, а потом сделать замену.

Проще разобрать на примерах:

Пример 9

Как и любой пример на логарифмы, начинаем с ОДЗ:

В уравнении один из логарифмов в квадрате, поэтому представить в виде равенства двух логарифмов, как мы делали в предыдущих примерах, не получится. Кроме этого, замечаем, что у нас оба логарифма абсолютно одинаковые: у них одинаковые основания и одинаковые аргументы.

Попробуем сделать замену:
$$t=log_{2}(x)$$
Тогда наше уравнение после замены примет вид:
$$t^2-5t+6=0;$$
$$D=25-24=1;$$
$$t_{1}=\frac{5+1}{2}=3;$$
$$t_{2}=\frac{5-1}{2}=1;$$
И сделаем обратную замену, получив два простых логарифмических уравнения:
$$t_{1}=\log_{2}(x)=3;$$
$$\log_{2}(x)=\log_{2}(2^3);$$
$$x_1=8.$$

$$t_{2}=\log_{2}(x)=1;$$
$$\log_{2}(x)=\log_{2}(2^1);$$
$$x_2=2.$$
Обязательно не забываем проверить, удовлетворяют ли корни ОДЗ \((x>0)\). Оба корня подходят, записываем ответ.Ответ: \(x_1=8; \, x_2=2.\)

Пример 10

Как обычно, начинаем с ОДЗ:
$$ \begin{cases}
\frac{8}{x}>0, \\
\log_{2}(16x)\neq0,\\
16x>0.\\
\end{cases}$$

Решаем каждое из получившихся неравенств в системе:
$$ \begin{cases}
x>0, \\
x\neq\frac{1}{16},\\
x>0.\\
\end{cases}$$
В итоге, ОДЗ будет: \(x\in(0;\frac{1}{16})\cup(\frac{1}{16};\infty)\).

Посмотрим теперь на сам пример. Видим два логарифма, у них одинаковые основания, что хорошо. Но функции, стоящие под логарифмами, разные. Постараемся при помощи свойств логарифма сделать одинаковые аргументы, чтобы потом сделать замену.

Воспользуемся формулами суммы и разности логарифмов с одинаковыми основаниями:
$$\log_{a}(b*c)=\log_{a}(b)+\log_{a}(c);$$
$$\log_{a}\left(\frac{b}{c}\right)=\log_{a}(b)-\log_{a}(c);$$
$$\log_{2}\left(\frac{8}{x}\right)=\log_{2}(8)-\log_{2}(x)=$$
$$=3-\log_{2}(x);$$
$$\log_{2}(16x)=\log_{2}(16)+\log_{2}(x)=$$
$$=4+\log_{2}(x);$$
Подставим наши преобразования в исходное уравнение
$$3-\log_{2}(x)-\frac{10}{4+\log_{2}(x)}=0;$$
Теперь в уравнении все логарифмы одинаковые, можем сделать замену. Пусть \(t=\log_{2}(x):\)
$$3-t-\frac{10}{4+t}=0;$$
Приводим к общему знаменателю
$$\frac{(3-t)(4+t)-10}{4+t}=0;$$
$$\frac{-t^2-t+2}{4+t}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-t^2-t+2=0;$$
$$t_{1}=1;$$
$$t_{2}=-2;$$
Делаем обратную замену:
$$t_{1}=\log_{2}(x)=1;$$
$$\log_{2}(x)=\log_{2}(2^1);$$
$$x_1=2.$$

$$t_{2}=\log_{2}(x)=-2;$$
$$\log_{2}(x)=\log_{2}({2}^{-2});$$
$$x_2=\frac{1}{4}.$$
Сверяем с ОДЗ, видим, что оба корня подходят, записываем ответ.Ответ: \(x_1=2; \, x_2=\frac{1}{4}.\)

Пример 11

Логарифм произведения и логарифм частного

loga(bc)=logab+logac(a>0,a≠1,b>0,c>0)

(5)

logabc=logab-logac(a>0,a≠1,b>0,c>0)

(6)

Я бы предостерег школьников от бездумного использования этих формул при решении логарифмических уравнений и неравенств. При использовании «слева направо» ОДЗ сужается, а при переходе от суммы или разности логарифмов к логарифму произведения или частного расширяется ОДЗ.

На самом деле фраза

журнал (е (х) г (х))

определяется в двух случаях: когда обе функции строго положительны или когда f(x) и g(x) меньше нуля.

Преобразуйте это выражение в сумму

logaf(x)+logag(x)

, мы должны ограничиться случаем, когда f(x)>0 и g(x)>0. Это сужение диапазона допустимых значений, что категорически недопустимо, так как может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Если перед логарифмом стоит число

Если перед логарифмом стоит число, как можно преобразовать это выражение?

Если перед логарифмом стоит число, это число можно записать в показатель степени выражения под знаком логарифма:

(x>0).

Например,

Вместе с суммой логарифмов и разностью логарифмов это свойство часто встречается при упрощении выражений с логарифмами, при решении логарифмических уравнений, неравенств и их систем.

А как умножить число на логарифм в квадрате? В кубе?

Если число стоит перед n-й степенью логарифма, то в показатель степени можно записать корень n-й степени из этого числа (при условии, что такой корень существует):

В частности,

Например,

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Логарифмы, примеры решений

Теория про логарифмы

Логарифм по основанию 10 называется десятичным логарифмом и обозначается :

а логарифм по основанию называют натуральным и обозначают :

Примеры

Задание

Вычислить значение выражения

Решение
Перейдем в каждом из слагаемых к логарифму по основанию 18, используя формулу перехода . Получим:

Так как сумма логарифмов равна логарифму произведения, последняя сумма перепишется в виде:

Число 324 можно представить как степень 18, получим

далее выносим степень как коэффициент перед знаком логарифма:

Учитывая, что , окончательно будем иметь:

Ответ

Задание	Вычислить
Решение

Перейдем во всех логарифмах к основанию 2, используя формулу перехода к новому основанию:

получим

Представим 4 и 8 в виде степени двойки и вынесем полученные степени за знак логарифма как коэффициент:

Ответ

Понравился сайт? Расскажи друзьям!

Виды логарифмов

• loga b — основание логарифма b (a > 0, a ≠ 1, b > 0)
• lg b — логарифм по основанию 10 (логарифм по основанию 10, а = 10).
• ln b — натуральный логарифм (логарифм по основанию e, a = e).

Сумма логарифмов. Разница логарифмов

Можно складывать логарифмы с одинаковым основанием:
Логарифмы с одинаковым основанием можно вычитать:
Мы видим, что исходные выражения состояли из логарифмов, которые отдельно не вычисляются, а используя свойства логарифмов, мы получили нормальные числа. Поэтому повторяем, что основные свойства логарифмов необходимо знать!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковым основанием! Если базы разные, эти свойства использовать нельзя!

Удаление степени из логарифма:

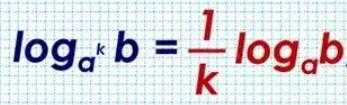
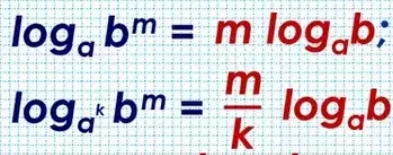
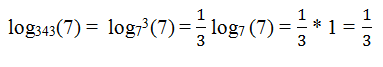
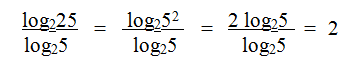
Переход к новому основанию

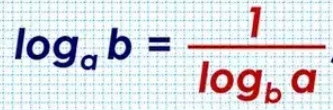
Когда мы анализировали формулы суммы и разности логарифмов, мы учитывали, что основания логарифмов должны быть одинаковыми. А если основания логарифмов разные? Используйте переход к новому базовому свойству.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Возьмем пример.

Необходимо найти значение такого выражения
Во-первых, мы преобразуем каждый логарифм, используя свойство взятия степени из логарифма:

Теперь используем переход к новому основанию для второго логарифма:
Подставляем результаты в исходное выражение:

Как решать логарифмы?

Логари́фм числа b по основанию a является показателем степени, которая требует, чтобы в число b возвели основание а. Полученный результат произносится так: “логарифм b по основанию а”. Решение логарифмических задач состоит в том, что вам необходимо определить данную степень по числам по указанным числам. Существуют некоторые основные правила, чтобы определить или решить логарифм, а также преобразовать саму запись. Используя их, производится решение логарифмических уравнений, находятся производные, решаются интегралы и осуществляются многие другие операции. В основном, решением самого логарифма является его упрощенная запись. Ниже приведены основные формулы и свойства:

Для любых a
; a
> 0; a
≠ 1 и для любых x
; y
> 0.

• a
  log a b
  = b
  – основное логарифмическое тождество
• log a
  1 = 0
• log a a
  = 1
• log a
  (x · y
  ) = log a x
  + log a y
• log a
  x/
  y
  = log a x
  – log a y
• log a
  1/x
  = -log a x
• log a x p
  = p
  log a x
• log a k x
  = 1/k
  · log a x
  , при k
  ≠ 0
• log a x
  = log a c x c
• log a x
  = log b x/
  log b a
  – формула перехода к новому основанию
• log a x
  = 1/log x a