Стыдные вопросы о логарифмах: всё, что нужно знать программисту

Что такое потенцирование

Когда мы видим некую математическую зависимость между логарифмами от разных чисел или выражений, мы можем “убрать” знаки log и перенести эту зависимость непосредственно на данные числа или выражения. Проще говоря, вычислить значение выражения f(x) по loga f(x). Рассмотрим пример:

Вышеизложенное накладывает определенные ограничения на использование логарифмов. Как видите, они не могут высчитываться от отрицательных чисел, и их основания должны быть положительными и отличными от нуля. При решении уравнений, таких как приведенное в примере выше, приходится проверять вхождение корней в ОДЗ, и это тоже приносит определенные неудобства, хотя они исчерпываются многочисленными преимуществами использования логарифмирования и потенцирования при решении уравнений.

Свойства логарифмов

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что ac = b: log a b=c⇔ a c =b (a>0,a≠1,b>0)

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1

Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество

a log a b =b (a>0,a≠1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1

Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма

log a a=1 (a>0,a≠1) (3) log a 1=0 (a>0,a≠1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) (5)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение log a (f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f(x)+ log a g(x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма

log a b p =p log a b (a>0,a≠1,b>0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a (f (x) 2 =2 log a f(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).

a log a b =b (a>0,a≠1)

log a a=1 (a>0,a≠1)

log a 1=0 (a>0,a≠1)

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0)

log a b p =p log a b (a>0,a≠1,b>0)

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1)

log a b= 1 log b a (a>0,a≠1,b>0,b≠1)

Правила действий над логарифмами и их основные свойства

Логарифмы не перестали приносить пользу и в эпоху компьютеризации. Например, в информатике очень часто используется бинарный (двоичный) log2. По-прежнему для оптимизации сложных математических действий используется сложение, вычитание и сравнение логарифмов чисел. Во всех этих операциях используются правила и свойства, описанные ниже:

• log_a 1 = 0. Показателем степени, в которую нужно возвести любое число, чтобы получить 1, всегда является ноль.
• log_a = 1. Это легко понять, поскольку результатом возведения любого числа в первую степень будет само это число.
• log_a xy = log_ax + log_ay. Именно на это свойство опирается приведенный выше способ умножения чисел. Как вы помните из школьного курса алгебры, когда мы умножаем степени с одинаковыми основаниями, показатели складываются — это объясняет данное правило.
• log_a x/y = log_ax — log_ay. Вы могли догадаться, что это свойство находит применения в вычислениях, связанных с делением больших чисел (при делении степеней с неким общим основанием a показатели вычитаются).
• log_a xp = p * log_ax. Данное свойство позволяет применять логарифмирование в операциях, связанных с возведением числа в степень p. Согласно алгебраическому правилу, при возведении степени в степени в степень показатели умножаются.

Как видите, можно значительно упростить сложные задачи с помощью этих правил. Именно поэтому французский ученый XIX века Лаплас говорил, что изобретение логарифма облегчило труд астрономов (вынужденных выполнять трудоемкие математические действия над большими величинами). Чтобы решать такие задачи, связанные с умножением, делением, возведением в степень, стало достаточно лишь произвести сложение, вычитание и умножение логарифмов соответствующих чисел.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

История.

Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен в глубь истории вплоть до древневавилонской математики (около 2000 до н.э.). В те времена интерполяция между табличными значениями целых положительных степеней целых чисел использовалась для вычисления сложных процентов. Гораздо позже Архимед (287–212 до н.э.) воспользовался степенями числа 10 8 для нахождения верхнего предела числа песчинок, необходимого для того, чтобы целиком заполнить известную в те времена Вселенную

Архимед обратил внимание на свойство показателей степеней, лежащее в основе эффективности логарифмов: произведение степеней соответствует сумме показателей степеней. В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями

М.Штифель в своем сочинении Арифметика целых чисел
(1544) привел таблицу положительных и отрицательных степеней числа 2:

Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.

По-видимому, правила, аналогичные правилам Штифеля, привели Дж.Нейпера к формальному введению первой системы логарифмов в сочинении Описание удивительной таблицы логарифмов
, опубликованном в 1614. Но мысли Непера были заняты проблемой превращения произведений в суммы еще с тех пор, как более чем за десять лет до выхода своего сочинения Непер получил из Дании известие о том, что в обсерватории Тихо Браге его ассистенты располагают методом, позволяющим превращать произведения в суммы. Метод, о котором говорилось в полученном Непером сообщении, был основан на использовании тригонометрических формул типа

поэтому таблицы Нейпера состояли главным образом из логарифмов тригонометрических функций. Хотя понятие основания не входило в явном виде в предложенное Непером определение, роль, эквивалентную основанию системы логарифмов, в его системе играло число (1 – 10 –7)ґ10 7 , приближенно равное 1/e
.

Независимо от Нейпера и почти одновременно с ним система логарифмов, довольно близкая по типу, была изобретена и опубликована Й.Бюрги в Праге, издавшем в 1620 Таблицы арифметической и геометрической прогрессий
. Это были таблицы антилогарифмов по основанию (1 + 10 –4) ґ10 4 , достаточно хорошему приближению числа e
.

В системе Нейпера логарифм числа 10 7 был принят за нуль, и по мере уменьшения чисел логарифмы возрастали. Когда Г.Бриггс (1561–1631) навестил Непера, оба согласились, что было бы удобнее использовать в качестве основания число 10 и считать логарифм единицы равным нулю. Тогда с увеличением чисел их логарифмы возрастали бы. Таким образом мы получили современную систему десятичных логарифмов, таблицу которых Бриггс опубликовал в своем сочинении Логарифмическая арифметика
(1620). Логарифмы по основанию e
, хотя и не совсем те, которые были введены Нейпером, часто называют нейперовыми. Термины «характеристика» и «мантисса» были предложены Бриггсом.

Первые логарифмы в силу исторических причин использовали приближения к числам 1/e
и e
. Несколько позднее идею натуральных логарифмов стали связывать с изучением площадей под гиперболой xy
= 1 (рис. 1). В 17 в. было показано, что площадь, ограниченная этой кривой, осью x
и ординатами x
= 1 и x
= a
(на рис. 1 эта область покрыта более жирными и редкими точками) возрастает в арифметической прогрессии, когда a
возрастает в геометрической прогрессии. Именно такая зависимость возникает в правилах действий над экспонентами и логарифмами. Это дало основание называть нейперовы логарифмы «гиперболическими логарифмами».

Исследование логарифмической функции

Определение:

Логарифмической функцией называется функция вида

Напомним, что в качестве основания логарифмов выбирается число а> 0, отличное от 1.

Основные свойства логарифмической функции (схема X).

• 1) Область определения: множество всех положительных чисел, т. е. промежуток (0; + ∞).
• 2) Монотонность: если а>1, то логарифмическая функция строго возрастает; если 0<а<1, то она строго убывает.
• 3) Область значений: множество всех вещественных чисел R.

Так как определение логарифмов основано на понятии степени,

то при доказательстве свойств логарифмической функции используют свойства показательной функции.

Свойство 1 в доказательстве не нуждается: оно опирается на определение логарифма числа х, по которому необходимо, чтобы число х было положительным.

Докажем свойство 2. Для этого сначала рассмотрим случай а>1. Возьмем два положительных числа х1 и x2, такие, что x1 <x2, и докажем, что Обозначив первое из этих чисел через t1, второе — через t2, по определению логарифма получим

Если бы выполнялось неравенство t1 ≥ t2, то по свойству монотонности показательной функции выполнялось бы неравенство т. е. Это противоречит условию.

Следовательно, t1<t2, что и требовалось доказать. Случай 0<а<1 рассматривается аналогично.

Свойство 3 утверждает, что всякое вещественное число t может быть логарифмом некоторого числа х. Так как степень определена при любом t, то, взяв х =, получим что и требовалось доказать.

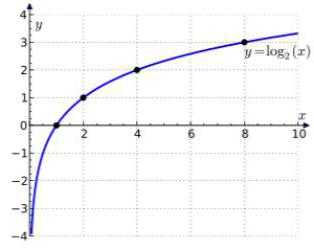
Графики логарифмических функций при различных основаниях показаны на рисунке 108.

Графики функций симметричны друг другу относительно прямой у = х. Действительно, если точка Р {с; d) лежит на графике функции у = ах, то d = ac. Но тогда и точка Q {d; с) лежит на графике функции

Так как точки Р (с; d) и Q (d; с) симметричны относительно прямой у = х (рис. 109), то симметричны и графики показательной и логарифмической функций.

Вместо логарифмических функций с произвольным основанием удобно рассматривать функции вида у = с ln х. Так как то указанные функции исчерпывают все логарифмические функции.

Функция у = ln х растет с ростом х, однако медленнее, чем любая степенная функция вида (k>0), в частности медленнее, чем (схема IX).

Производная логарифмической функции

Рассмотрим две функции у = и у = ln х. Мы знаем, что их графики симметричны относительно прямой у = х. Это поможет нам найти производную логарифмической функции, зная производную экспоненты. Возьмем точку Р (с; d) на графике экспоненты (т. е. d = ec) и симметричную точку Q (d; с) на графике логарифмической функции (т. е. c = lnd). Касательные к графикам в этих точках тоже будут симметричны (рис. 109). Угловой коэффициент k1 касательной к графику экспоненты равен значению производной функции у = ех при х = с, т. е. k1=ec, так как

Пусть a1 и а2 — углы, образованные проведенными касательными с осью абсцисс. Из рисунка 109 ясно, что

Так как

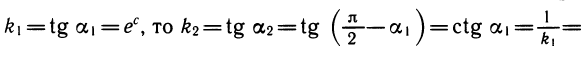
Таким образом, производная функции у = ln х в точке x = d равна

Можно написать:

Мы видим, что производная логарифмической функции y = ln х равна степенной функции . Интересно заметить, что функция не получается как производная какой-либо другой степенной функции вида у = схк. Действительно, хотя при любом к, но получить значение к— 1, равное —1, можно лишь при k = 0, а (x°)’ = 0.

Так как то

По формулам производной показательной функции и

Известно, что ,где k= ln а. Поэтому т. е.

Примеры:

Зная производные экспоненты и логарифма, можно получить приближенные формулы для их вычисления.

Пусть

Разность —это приращение у на отрезке . Вычислив dy при хо = 0, получим dy = y’ (0) dx. Так как у’ = ех, то у'(0)= 1. Заменив ∆у на dy и подставив dx = h, получим приближенную формулу

Более точная формула для вычисления экспоненты такова:

Пусть теперь у =lnх. Выберем дго=1, xо = ln l =0. Положим dx = h и вычислим ln (l+h). Найдем dy при xo=1. Так как

(In то y’ (jc0)= 1 и dy= 1 •dx = h.

Заменяя ∆y= ln (1+h) — ln l = ln (l+h), получаем приближенную формулу

Более точная формула для вычисления логарифма такова:

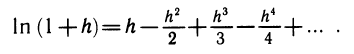
Основные свойства логарифмов

Теорема:

При всех положительных значениях b и c справедливо равенство:

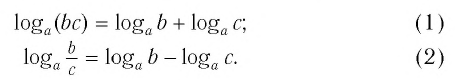
Доказательство:

Докажем утверждение (1).

По основному логарифмическому тождеству

по характеристикам степени

Таким образом, мы имеем:

Отсюда получаем равенство (1).

Докажем утверждение (2). Преобразуем левую часть равенства (2):

I используя равенство (1), получаем

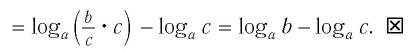
Заметим, что равенство (2) можно доказать так же, как и равенство (1) – сделать это самостоятельно.

Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.

Равенство (2) означает, что логарифм дроби с положительными числителем и знаменателем равен разности между логарифмами числителя и знаменателя.

Комментарий. Равенства, доказанные в теореме 1 (как и другие равенства в этом пункте), являются тождествами. Фактически каждое из них превращается в истинное числовое равенство для всех значений a, b и c, для которых выражения, входящие в равенство, имеют смысл.

Теорема:

Для всех значений s и положительных значений b выполняется равенство

Доказательство:

По основному логарифмическому тождеству

по характеристикам степени

Таким образом, у нас есть

Таким образом, вследствие п. 2.3 мы получаем равенство (3).

Следствие 1. Если числа
одного и того же знака, то подобие

Следствие 2. Для любого целого числа
есть сходство

Пример №1

Найдите значение выражения:

Решение:

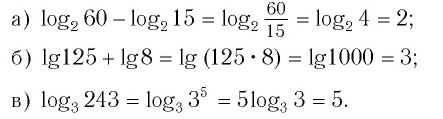
Отвечать:

Теорема:

Для всех значений
и
истинное равенство

Доказательство:

Способ 1. Согласно основному логарифмическому тождеству имеем

Логарифмируя левую и правую части этого тождества по основанию а, получаем

Используя тождество (3), имеем

Потому что
Следовательно, левую и правую части этого равенства можно разбить на
В результате получаем тождество (6).

Способ 2. Пусть
после этого
Логарифмируя обе части этого равенства по основанию а, получаем

Где мы получаем

Так,

Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.

Обычно в таблицах-калькуляторах приводятся значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по основанию числа к логарифм другого основания.

Следствием тождества (6) с основанием a = c является формула

(убедитесь в этом сами).

Пример №2

Найдите значение выражения, если

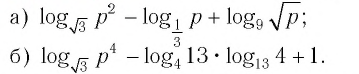
Решение:

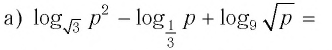
согласно тождеству (6) имеем

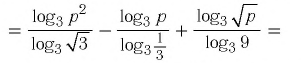
используя тождество (3), получаем

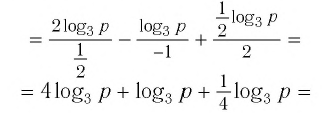
используя тождество (1), имеем

при условии
мы получаем

6)

на основании тождеств (6) и (7) получаем

по тождеству (3) и с учетом условия имеем

Отвечать:

Следствие 3. Применяются следующие тождества:

Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого раздела.

Пример №3

Упростить выражения

Решение:

Используя определение логарифма, представим числа 1 и 3 как логарифмы по основанию 2:

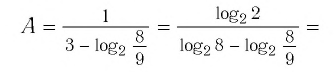
по свойству (2) логарифмов имеем

используя формулу (7), получаем

Отвечать:

Развитие науки, особенно астрономии, уже в 16 веке привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.

Свойство основного логарифмического тождества

Существует несколько основных особенностей при выполнении расчетов с логарифмами и логарифмическими тождествами.

Можно выделить три основных правила:

1. Число а не равняется единичному значению \. При возведении числа в степень, которая равна единичному значению, всегда получаем число один. Равенство вида \ может существовать только при значении b=1. При возведении логарифмов значение один получим любое действительное число.
2. Значение a>0. Логарифм для a=0 согласно определению может существовать лишь при b=0. Так как при возведении в любую степень нулевого значения получается ноль, то \ может быть любое действительное число. Чтобы избежать неоднозначности, чаще всего принимают \. При значении а рациональных и иррациональных значений логарифма, потому что степень с рациональным и иррациональным значением может определяться только для оснований с положительным значением. Чтобы избежать данной ситуации, следует принимать  a>0 .
3. Если значение b>0.  Основное логарифмическое тождество довольно часто используется для упрощения всех логарифмических выражений.