Логарифм — формулы, свойства и примеры с решением

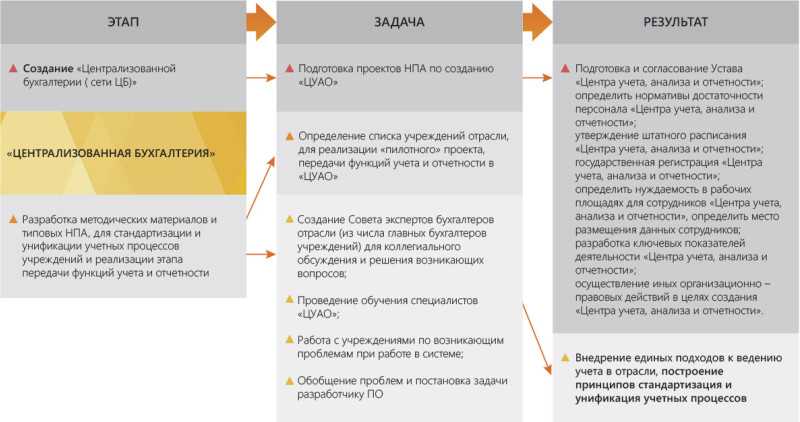
Что такое логарифм?

Лучший способ понять это — решить уравнения графически. Нарисуем график и с его помощью решим уравнения:

х=1

х=2

Большой! Теперь решим уравнение .

И в этом случае нельзя назвать точное значение, то есть мы понимаем, что корень больше единицы и меньше двух, но более точных данных нет.

Это корень, данный логарифмом, а именно (читается как «логарифм пяти по основанию три» или «логарифм по основанию три из пяти»).

Смысл мы определили — теперь перейдем к общему определению логарифма.

Логарифм b по основанию a — это показатель степени с основанием a, равным b. То есть, проще говоря, логарифм — это степень, в которую нужно возвести a, чтобы получить b. Однако логарифм имеет условия или ограничения, при которых основание a больше нуля и не равен единице, а показатель степени b больше нуля.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Что такое логарифм — понятие и определение

Благодаря логарифмам можно значительно упростить сложные алгебраические операции, к примеру, вместо умножения выполнить сложение, заменить возведение в степень умножением или делением. Таким образом, удобно решать громоздкие формулы. Для понимания метода применения логарифма можно рассмотреть практический пример. Предположим, что требуется найти решение следующего уравнения:

\(\displaystyle {{2}^{x}}=8\)

В начале следует определить степень, в которую можно возвести число 2, и в результате получить число 8. Решение подразумевает использование способа подбора чисел. Возводя 2 в степени, можно выяснить, что в третьей степени 2 равна 8. Вывод:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

\((\displaystyle {{2}^{3}}=8)\)

В результате ответом к задаче будет число 3.

Разберем второй пример:

\(\displaystyle {{2}^{x}}=5\)

Использовать главный метод подбора, как в предыдущем уравнении, не получится, так как работать предстоит не с целыми и даже не с рациональными числами. В данном случае целесообразно оперировать понятием логарифма. Запись будет иметь следующий вид:

\(\displaystyle x={{\log}_{2}}5\)

В общем виде логарифм записывают, таким образом: 

Логарифмом по основанию a от аргумента x является степень, в которую следует возвести число a, чтобы получить число x.

рекуррентные отношения — логарифмы с дробью в качестве основания

спросил 4 года 10 месяцев назад

Изменено
4 года, 10 месяцев назад

Просмотрено
11 тысяч раз

$\begingroup$

Как решить логарифмическое выражение, основанием которого является дробь? В моем примере я пытаюсь решить следующее: 9{\log_\frac{3}{2}(1)} \tag{1} $$

Это связано с использованием «главной теоремы» для решения рекуррентных соотношений. Люди обычно приводят примеры, где они решают что-то вроде:

$$ {\log_\frac{1}{3}(27)} \tag{2} $$

, что кажется простым для понимания.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Объяснение и примеры, показатели, доказательства

Законы логарифмов — это правила, которые можно применять для упрощения и решения сложных логарифмических уравнений.

Основные законы бревен

Формула изменения закона находится в буклете с формулами, который вам дадут на экзамене.

Доказательство закона логарифмов

Не обязательно уметь доказывать каждый закон логарифма для экзамена, но важно понимать каждый шаг и почему он происходит

Закон произведения (сложения)

1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.

Для , основание равно x, показатель степени равен c , ответ на показатель степени равен a .

Следовательно, это можно записать как

Для , основание равно x, показатель степени равен d , а ответ на показатель степени равен b.

Следовательно, это можно записать как

2. Таким образом, используя наше экспоненциальное (индексное) правило,

3.

4. Поскольку включает как экспоненту с основанием x , так и логарифм с основанием x (), они компенсируют друг друга, чтобы стать просто c + d.

Этот шаг связан с тем, что логарифмы и экспоненты являются обратными функциями друг друга. Подумайте о том, когда мы компенсируем +4 и -4 в x +4 -4 = 10 — это тот же принцип.

5. Мы определили c и d в части 1. и

Следовательно,

Правило частных

1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.

Ибо, основание равно x, показатель степени равен c, и ответ на показатель степени равен a .

Следовательно, это можно записать как

Для , основание равно x, показатель степени равен d, и ответ на показатель степени равен б.

Следовательно, это можно записать как

2.

3. Возьмем журнал обеих сторон.

4. Поскольку включает экспоненту с основанием x и логарифм с основанием x , они компенсируют друг друга и становятся просто c — d .

5. Мы определили c и d в части 1 где и :

Изменение основания

1. Пусть, где основание a , показатель степени равен k, и x экспоненциальный ответ на x .

Следовательно, его можно переписать в экспоненциальном виде:

2. Возьмите логарифм обеих сторон

3. Используйте степенное правило для упрощения

, которое затем можно подставить обратно в уравнение

4. Перестроить, чтобы получить k самостоятельно путем деления на

5. Поскольку k уже определено, его можно подставить в уравнение как использование наших экспоненциальных правил с негативами.

Вы можете использовать правило журнала питания, чтобы уменьшить -1, как это делается.

Журнал базы

1. Набор, где база а, 9Показатель степени 0012 равен x, , а ответ на экспоненту равен a . Поэтому его можно записать как.
2. В соответствии с экспоненциальными правилами, если ответ экспоненты равен основанию, то показатель степени должен быть равен 1.

Логарифм 1

1. Набор, где основание равно a, показатель степени равен x, и ответ на экспоненту равен 1. Следовательно, это можно записать как.
2. В соответствии с экспоненциальными правилами, если ответ экспоненты равен 1, то показатель степени должен быть равен 0.

Упрощение и решение с использованием законов бревен

Здесь мы рассмотрим несколько примеров упрощения ряда законов бревен.

Упрощение и решение с использованием 1 логарифмического закона

Показать логарифм (6) + логарифм (4) = логарифм (24)

логарифм (6) + логарифм (4) = логарифм (6 x 4) = логарифм (24)

Лог решения (14) — Лог (7)

Лог (14) — Лог (7) = Лог (14/7) = Лог (2) = 0,301 (3 ст.

Упростить 2логарифм (9), сохранить точная форма

Решить

Упрощение и решение с использованием законов множественных журналов

Возможно, будет полезно использовать правила, которые упрощают отдельные журналы, перед выполнением законов упрощения множественных журналов.

Решить

Упростить

Доказать, где

1. Используя правило степени, .

Следовательно,

2. Используя правило отношения,

3. Когда вы хотите удалить логарифм, вам нужно преобразовать его в экспоненту. Это работает так же, как обычно — просто убедитесь, что вы пометили каждую часть.

Основание равно 2; показатель степени равен 3; ответ на экспоненциальный

4. Решите как обычное уравнение являются законом продукта, частным законом, изменением основного закона и правилом силы.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ — диапазон допустимых значений переменных).

Мы помним, что, например, из отрицательных чисел нельзя извлечь квадратный корень; или если у нас есть дробь, то знаменатель не может быть равен нулю. Аналогичные ограничения действуют и для логарифмов:

То есть и аргумент, и базовое число должны быть больше нуля, а базовое число не может быть равно .

Почему?

Начнем с простого: скажем так. Тогда, например, числа не существует, так как какую бы мощность мы ни поднимали, оно всегда оказывается . Кроме того, он не существует ни для кого. Но в то же время он может быть подобен чему угодно (по той же причине — подобен в любой степени). Поэтому объект не представляет интереса, и его просто выкинули из математики.

Аналогичная проблема у нас и в случае : при любой положительной степени это есть, и его вообще нельзя возводить в отрицательную степень, так как получится деление на ноль (напомню).

Когда мы сталкиваемся с задачей возведения в дробную степень (что представляется в виде корня: . Например (то есть), а не существует.

Поэтому негативные причины легче выбросить, чем с ними возиться.

Ну, так как основание а для нас только положительное, мы всегда будем получать строго положительное число, в какую бы степень мы его ни возводили. Так что аргумент должен быть положительным. Например, его не существует, так как оно не будет ни в какой степени отрицательным числом (и даже нулем, поэтому его тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Я приведу пример:

Давайте решим уравнение .

Запомните определение: логарифм — это степень, в которую нужно возвести основание, чтобы получить аргумент. И по условию эта степень равна : .

Получаем обычное квадратное уравнение: Решим ее с помощью теоремы Виета: сумма корней равна , а произведение . Легко получить, это числа и .

А вот если сразу взять и записать в ответ обе эти цифры, то можно получить 0 баллов за задание. Почему? Давайте подумаем, что произойдет, если мы подставим эти корни в исходное уравнение?

— Верно.

— это явно неверно, так как основание не может быть отрицательным, то есть корень «сторонний».

Чтобы избежать таких неприятных фокусов, запишите ОДЗ самостоятельно перед тем, как приступить к решению уравнения:

Итак, после получения корней и , сразу отбрасываем корень и пишем правильный ответ

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где а — основание логарифма,

где а — основание логарифма,

b — аргумент логарифма

Чтобы найти значение логарифма, приравняем его к X.
и преобразовать в
и преобразовать в Помните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было проще, можно запомнить так — основание всегда остается внизу (и в первом, и во втором выражении а внизу)!

Вот пример:

Чтобы вычислить этот логарифм, приравняйте его к X и используйте правило, описанное выше:
В какую степень нужно возвести 2, чтобы получилось 8? Конечно, в третьей степени, вот так:

Еще раз отмечу, что основание (в нашем случае это 2) всегда внизу, и это то, что возведено в степень.

Еще раз отмечу, что основание (в нашем случае это 2) всегда внизу, и это то, что возведено в степень.

Еще примеры:

10 примеров логарифмов с решением

1. Найдите значение выражения
2. Найдите значение выражения
3. Найдите значение выражения
3. Найдите значение выражения4. Найти значение выражения
5. Найдите значение выражения
5. Найдите значение выражения6. Найти значение выражения
Сначала найдем значение
Сначала найдите значение. Для этого приравняем его к X:
Тогда исходное выражение принимает вид:

7. Найдите значение выражения
7. Найдите значение выражения Преобразуем наше выражение:
Теперь мы используем это свойство, чтобы вывести показатель степени из логарифма и получить:
8. Найдите значение выражения
8. Найдите значение выражения Так как основания у логарифмов одинаковые, воспользуемся свойством разности логарифмов:
9. Найдите значение выражения
9. Найдите значение выражения. Поскольку основания логарифмов разные, нельзя использовать свойство суммы логарифмов. Поэтому решаем каждый логарифм отдельно:
Подставляем полученные значения в исходное выражение:

4 + 3 = 7

10

Найдите значение выражения
Обратите внимание, что это выражение не является произведением логарифмов. Для логарифма по основанию 4 выражение подлогарифма равно log216

Поэтому сначала находим значение log216, а потом подставляем результат в log4:
Обратите внимание, что это выражение не является произведением логарифмов. Для логарифма по основанию 4 выражение подлогарифма равно log216. Поэтому сначала находим значение log216, а потом подставляем результат в log4:

Надеюсь, теперь вы понимаете, что такое логарифм.

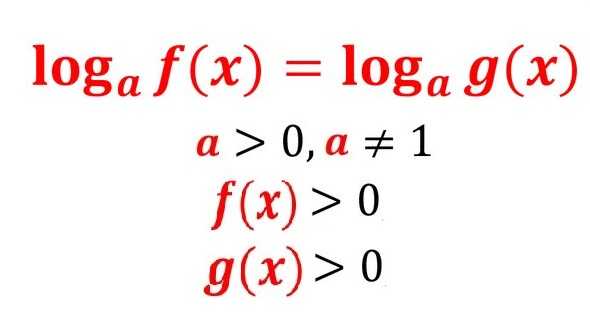
Логарифмическое уравнение: решение на примерах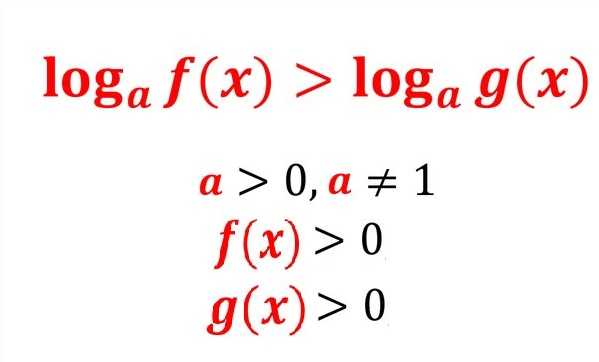
Логарифмическое неравенство: Решение с примерами

Пример 1 Найдите корень уравнения.

по определению логарифма:

Все неизвестные переносятся в левую часть уравнения (слева от =), а известные — в правую.

Мы получаем:

Давай проверим:

Отвечать:

Пример 2. Найдите корень уравнения.

Здесь для решения этого логарифмического уравнения воспользуемся свойством логарифма:

То есть мы должны ввести цифру 3 справа под знаком логарифма.

или

Если показатели равны, основания степени равны, то числа, полученные в результате, равны, то есть получаем

Давай проверим:

Мы используем следующее свойство для логарифма:

Затем мы получаем:

Давай проверим:

Отвечать:

Пример 4. Найдите корень уравнения.

Используя определение логарифма, получаем:

Давай проверим:

Отвечать: .

Таким образом, теперь вы можете создавать четкие инструкции по решению логарифмических уравнений. Он состоит из следующих шагов:

1. Справа и слева от знака равенства (=) составить логарифмы по одному основанию, а от коэффициентов перед логарифмами избавиться, используя свойства логарифмов.
2. Мы избавляемся от логарифмов, используя правило возведения в степень. Остаются только те числа, которые были под знаком логарифма.
3. Решаем полученное обыкновенное уравнение — как найти корень уравнения смотрите здесь.
4. Сделать чек
5. Записываем ответ.

Что такое Логарифм

Логарифм — это математическая функция, основанная на свойствах возведения в степень.

Значение логарифма соответствует показателю степени данной базы, равному положительному числу “b” в базе “a”, что также должна быть положительной и отличаться от 1.

Чтобы лучше понять концепцию логарифма, необходимо посмотреть на формулу логарифмического уравнения:

“a” = основание, которое должно быть больше нуля (a > 0) и отличаться от единицы (a ≠ 1).

“b” = логарифмируемое число, где b должно быть больше нуля (b > 0).

В этом уравнении мы хотим найти, в какую степень (х) нужно возвести a, чтобы получилось b, т. е. aˣ = b.

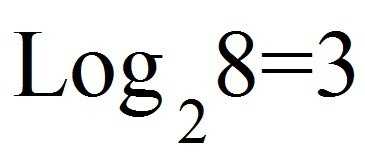, потому что

Формулы и свойства логарифмов

Некоторые из основных правил логарифма:

• Когда логарифмируемое число равно основанию логарифма, логарифм всегда будет равен 1 ;

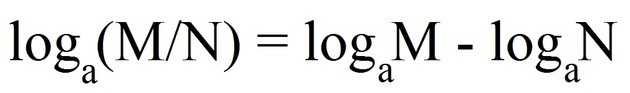
Формулы перехода к новому основанию:

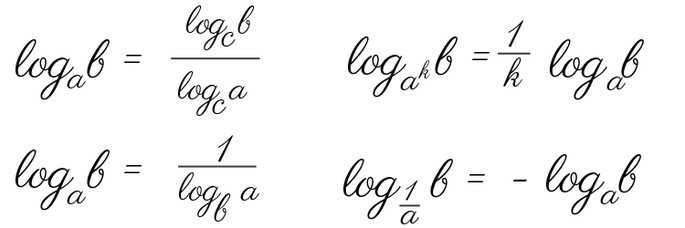
Решение логарифмов — примеры

ОДЗ логарифма

Как определить Область Допустимых Значений логарифма:

Для определения ОДЗ логарифма мы обращаем внимание только на то, что стоит в скобках, и указываем, что вся эта часть больше ноля

График логарифмической функции

Примерно таким образом может выглядеть график логарифмической функции (одна из линий на рисунке):

Свойства логарифмической функции :

• E (y) = R, множество значений — все действительные числа;
• область определения — множество всех положительных чисел D(y): (0;+∞);
• её график всегда проходит через точку (1;0);
• она не считается ни чётной, ни нечётной;
• у неё нет ни наибольшего, ни наименьшего значений;
• она не ограничена ни сверху, ни снизу;
• если 0<а<1 => функция убывает, а если a>1 => функция возрастает.

Логарифм Непера или натуральный логарифм

Состоит из логарифма, основанного на иррациональном числе, которое называется «число Эйлера», пишется как «e» и приблизительно равно 2,718281. Является обратной функцией к экспоненциальной функции.

Название логарифма («логарифм Непера») произошло от имени его изобретателя — математика Джона Непера.

Десятичный логарифм

Это наиболее распространённая модель математических вычислений, особенно в так называемых логарифмических шкалах (или логарифмическом масштабе). Например: шкала pH, шкала Рихтера интенсивности землетрясений, шкала частоты звука — нотная шкала, и другие. И характеризуется тем, что основание (её логарифма) равно 10.

Десятичный логарифм может быть представлен без указания его основания.

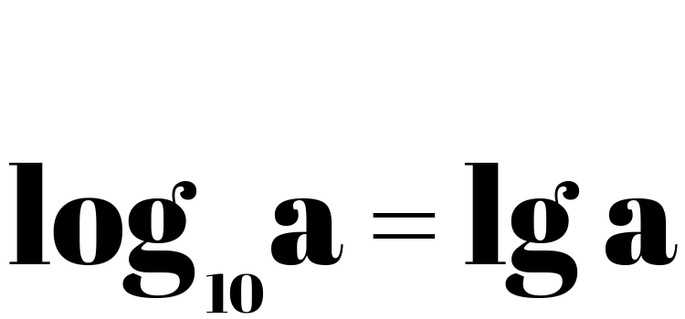
История логарифма

Первоначально концепция логарифма была создана шотландским математиком Джоном Непером (1550–1617) в 17-м веке, с целью упрощения сложных тригонометрических расчётов.

Английский математик Генри Бриггс (1561–1630) также внёс свой вклад в исследования логарифма и считается одним из ответственных за улучшение десятичного логарифма и за создание его современной версии.

Этимологически слово «логарифм» образовано объединением двух греческих терминов: λόγος — «основание» и ἀριθμός — «число».

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: logax и logay. Тогда их можно складывать и вычитать, причем:

1. logax + logay = loga (x · y);
2. logax − logay = loga (x: y).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного

Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Задача. Найдите значение выражения: log6 4 + log6 9.

Поскольку основания у логарифмов одинаковые, используем формулу суммы:log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.

Задача. Найдите значение выражения: log2 48 − log2 3.

Основания одинаковые, используем формулу разности:log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Задача. Найдите значение выражения: log3 135 − log3 5.

Снова основания одинаковые, поэтому имеем:log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Как решать уравнения с логарифмами: 2 способа с примерами

Есть много способов решить логарифмическое уравнение. Чаще всего в школе учатся решать логарифмическое уравнение, используя определение логарифма. То есть имеем уравнение вида:
Вспоминая определение логарифма, получаем следующее:
Мы запоминаем определение логарифма и получаем следующее: Это дает нам простое уравнение, которое мы можем легко решить.

При решении логарифмических уравнений важно помнить об области логарифмирования, поскольку аргумент f(x) должен быть больше нуля. Поэтому после решения логарифмического уравнения всегда делаем проверку!. Давайте посмотрим, как это работает на примере:

Давайте посмотрим, как это работает на примере:

Воспользуемся определением логарифма и получим:

2х + 3 = 32

Теперь у нас есть простейшее уравнение, решить которое несложно:

2х + 3 = 9

2х = 6

х = 3

Возьмем чек. Подставляем найденное X в исходное уравнение:
Поскольку 32 = 9, последнее выражение верно. Следовательно, x = 3 является корнем уравнения.

Ответ: х = 3

Главный недостаток этого метода решения логарифмических уравнений в том, что многие ребята путают, что нужно возводить в степень. То есть при преобразовании logaf(x) = b многие возводят не a в степень b, а b в степень a. Такая досадная ошибка может лишить вас ценных баллов на экзамене.

Поэтому покажем еще один способ решения логарифмических уравнений.

Чтобы решить логарифмическое уравнение, мы должны привести его к такому виду, чтобы и правая, и левая части уравнения имели логарифмы с одним и тем же основанием. Это выглядит так:

Когда уравнение приведено к такому виду, мы можем «вычеркнуть» логарифмы и решить простое уравнение. Давайте разберемся на примере.

Снова решим то же уравнение, но теперь так:
В левой части у нас есть логарифм с основанием 2. Следовательно, мы должны преобразовать правую часть логарифма так, чтобы она также содержала логарифм с основанием 2.

Для этого напомним свойства логарифмов. Первое свойство, которое нам нужно здесь, это логарифмическая единица измерения. Помните, что:
То есть в нашем случае:
То есть в нашем случае: Возьмем правую часть нашего уравнения и начнем ее преобразовывать:
Теперь нам нужно добавить 2 к логарифмическому выражению. Для этого вспомним еще одно свойство логарифма:

Используя это свойство в нашем случае, мы получаем:
Преобразовали правую часть нашего уравнения в нужный нам вид и получили:
Теперь у нас есть логарифмы с одинаковым основанием в левой и правой частях уравнения, поэтому мы можем их вычеркнуть. В результате получаем следующее уравнение:

2х + 3 = 32

2х + 3 = 9

2х = 6

х = 3

Ответ: х = 3

Да, операций в этом методе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего меньше вероятность ошибиться. Кроме того, этот метод дает больше возможностей для решения более сложных логарифмических уравнений.

Возьмем другой пример:
Затем, как и в предыдущем примере, воспользуемся свойствами логарифмов и преобразуем правую часть уравнения следующим образом:
Затем, как и в предыдущем примере, воспользуемся свойствами логарифмов и преобразуем правую часть уравнения следующим образом: После преобразования правой части наше уравнение принимает следующий вид:
Теперь мы можем вычеркнуть логарифмы и тогда получим:
Теперь можно вычеркнуть логарифмы и тогда получим: Запомните свойства степеней:

3х — 5 = 4

3х = 9

х = 3

Теперь проверяем:
то последнее выражение верно. Следовательно, x = 3 является корнем уравнения.

Ответ: х = 3

Другой пример решения логарифмического уравнения:
Во-первых, давайте преобразуем левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковым основанием. Воспользуемся свойством суммы логарифмов и получим:
Во-первых, давайте преобразуем левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковым основанием. Воспользуемся свойством суммы логарифмов и получим: Теперь преобразуем правую часть уравнения:
После выполнения преобразований правой и левой частей уравнения получили:
Выполнив преобразования правой и левой частей уравнения, мы получили: Теперь мы можем вычеркнуть логарифмы:

Решаем это квадратное уравнение, находим дискриминант:

Проверим, подставив x1 = 1 в исходное уравнение:
Проверим, подставив x1 = 1 в исходное уравнение:
Верно, поэтому x1 = 1 является корнем уравнения.

Теперь подставим x2 = -5 в исходное уравнение:
Поскольку аргумент логарифма должен быть положительным, выражение неверно. Следовательно, x2 = -5 — нечетный корень.

Ответ: х = 1

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!