2.3. Какие системы счисления используют специалисты для общения с компьютером
Кроме десятичной широко используются системы с основанием, являющимся целой
степенью числа 2, а именно:
- двоичная (используются цифры 0, 1);
- восьмеричная (используются цифры 0, 1, …, 7);
-
шестнадцатеричная (для первых целых чисел от нуля до девяти
используются цифры 0, 1, …, 9, а для следующих чисел — от десяти до
пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
|
|
Из всех систем счисления особенно проста и поэтому интересна для
технической реализации в компьютерах двоичная система счисления.
2.7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления
|
Для перевода правильной дроби из десятичной системы счисления в двоичную (восьмеричную, шестнадцатеричную) нужно умножить исходную дробь и дробные части получающихся произведений на основание, представленное в десятичной системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в двоичной (восьмеричной, шестнадцатеричной) системе счисления. |
Пример. Переведем число 0,36 из десятичной системы в двоичную,
восьмеричную и шестнадцатеричную:

| Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше. |
Да какая разница?
Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?
Рассмотрим примеры:
10 – 5 + 2 = ?
Если мы будем выполнять действия по порядку, получим:
- 10 – 5 = 5;
- 5 + 2 = 7.
Попробуем иначе:
- 5 + 2 = 7;
- 10 – 7 = 3.
Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:
25 – (18+2) = ?
Пробуем решить двумя способами:
- 25 – 18 + 2 = 9;
- 25 – 20 = 5.
Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:
- 18 + 2 = 20;
- 25 – 20 = 5.
Другого решения у ответа у примера быть не должно.
Итак:
Правило первое: Математические действия в выражении выполняются по порядку, начиная с левого, направо.
Правило второе: Если в выражении есть скобки, действие в скобках выполняется в первую очередь, а затем следуют действия по порядку, слева направо.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6.
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3, получаем 4, после чего к полученной разности 4 прибавляем 6, получаем 10.
Кратко решение можно записать так: 7−3+6=4+6=10.
Ответ:
7−3+6=10.
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
сначала 6 делим на 2, это частное умножаем на 8, наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2.
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь 4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3 найденное значение 10, а вместо 4:2 — значение 2, имеем 17−5·6:3−2+4:2=17−10−2+2.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7.
Ответ:
17−5·6:3−2+4:2=7.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Основы арифметики в классе
Основные арифметические операции выполняются на уроках математики в первые классы школы . В начальной школе ( ) арифметика сначала преподается с небольшими натуральными числами, а затем расширяется за счет включения более крупных чисел. Уроки также включают таблицы умножения, деление на остаток , решение простых уравнений и правило трех . Есть в ум , написанный арифметиком, вычисление опрокидывания и приложение в виде текстовых задач практиковали. Для удобного расчета используются простые законы расчета. В первые годы средней школы ( ) также рассматриваются отрицательные числа, вводятся дроби и, следовательно, рациональные числа, а также рассматриваются законы, относящиеся к связи четырех основных арифметических операций.
2.1. Что такое система счисления
| Система счисления — это способ представления любого числа посредством алфавита символов, называемых цифрами. |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который
она вносит в значение числа) не зависит от ее позиции в записи числа.
Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в
любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в
зависимости от ее положения (позиции) в последовательности цифр, изображающих
число. Например, в числе 757.7 первая семерка означает 7 сотен, вторая — 7
единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757.7 означает сокращенную запись выражения
5. 101 + 7.
10 + 7. 10—1 =
757,7.
Любая позиционная система счисления характеризуется своим основанием.
| Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления. |
За основание системы можно принять любое натуральное число — два, три, четыре
и т.д. Следовательно, возможно бесчисленное множество позиционных систем:
двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления
с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2
+ … + a1 q1 + a q +
a-1 q-1 + … + a-m q-m,
ainm
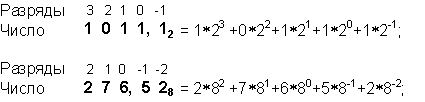
Четыре основных арифметических операции
добавление
| 1+2знак равно3{\ displaystyle 1 + 2 = 3} |
→ Основная статья : Дополнение
Сложение — это процесс совместного подсчета двух (или более) чисел. Оператором сложения является знак плюс +, операнды называются слагаемыми , термин сумма и результат называются суммой значение / значение суммы:
- Сложение + сложение = сумма значения
Результатом сложения натуральных чисел снова является натуральное число. При запоминании и используя элементарные арифметические методы , малые числа могут быть добавлены в вашей голове. Добавление больших чисел может производиться вручную с помощью письменного сложения .
вычитание
| 5-1знак равно4-й{\ displaystyle 5-1 = 4} |
→ Основная статья : вычитание
Вычитание — это вычитание одного числа из другого числа. Оператором вычитания является знак минус -, два операнда называются minuend и subtrahend , терминов и результат называется значением разности / значением разницы.
- Minuend — Subtrahend = значение разницы
Однако результатом вычитания двух натуральных чисел снова будет только натуральное число, если уменьшаемое больше, чем вычитаемое. Если minuend и subtrahend совпадают, результатом является число ноль , которое часто также считается среди натуральных чисел. Если вычитаемое больше минимального, результатом будет отрицательное число . Поэтому, чтобы иметь возможность выполнять вычитание без ограничений, диапазон чисел расширен до целых чисел . Вычитание больших чисел можно производить вручную с помощью письменного вычитания .
умножение
| 3⋅5знак равно15-е{\ Displaystyle 3 \ cdot 5 = 15} |
→ Основная статья : Умножение
Умножение — это взятие двух (или более) чисел. Оператор умножения — это знак · (или x), операнды — это вызываемый и умножаемое, термин продукт, а результат — стоимость продукта / стоимость продукта:
- Множитель · Множитель = стоимость продукта
Если нет необходимости проводить различие между множителем и множимым, их часто вместе называют .
Если множители являются натуральными или целыми числами, результатом умножения снова будет натуральное или целое число. Запоминая таблицы умножения, маленькие числа можно умножать в уме. Умножение больших чисел можно производить вручную с помощью письменного умножения .
разделение
| 12-е3знак равно4-й{\ displaystyle 12: 3 = 4} |
→ Основная статья : Дивизия (математика)
Деление — это процесс деления одного числа на другое. Оператором деления является знак деления (или ), два операнда называются делимым и делителем , термин частное и результат называется значением частного / значением частного:
- Дивиденд: делитель = частное значение
Однако результатом деления двух натуральных или целых чисел снова будет только натуральное или целое число, если делимое кратно делителю. В противном случае вы получите дробь . Поэтому, чтобы можно было выполнять деление без ограничений, диапазон чисел расширен за счет включения рациональных чисел . Однако деление на ноль не может быть определено осмысленно. Деление больших чисел можно производить вручную с помощью письменного деления .
Порядок действий в выражениях без скобок
Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:
- Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
- Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
- Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.
В качестве примера рассмотрим следующее выражение:
3 · 42 – 23 : 2 + 20
Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):
3 · 16 – 8 : 2 + 20
Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):
48 – 4 + 20
И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):
48 – 4 + 20 = 44 + 20 = 64
Первый способ
- Каждое действие записывается отдельно со своим номером под примером.
- После выполнения последнего действия ответ обязательно записывается в исходный пример.
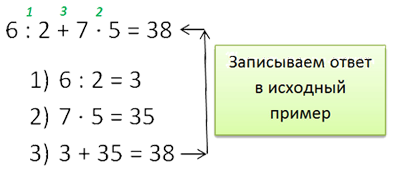
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ
Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.
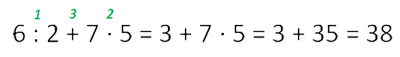
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
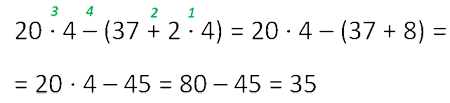
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
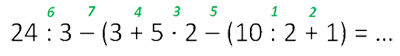

Математические действия с нулем
Круглый нуль такой хорошенький, Но не значит ничегошеньки.
В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:
5 × (8 : 2 – 4) = ?
- 8 : 2 = 4;
- 4 – 4 = 0;
- 5 × 0 = ?
При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:
0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;
Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:
0 : 5 = 0.
Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.
Напомним другие арифметические действия с нулем:
а + 0 = а;
0 + а = а (от перестановки слагаемых сумма не меняется);
а – 0 = а;
0 – а = — а (число, противоположное вычитаемому).
Задания для самостоятельного решения
Задание 1. Найдите значение выражения: 5 + 2 − 2 − 1 Решение
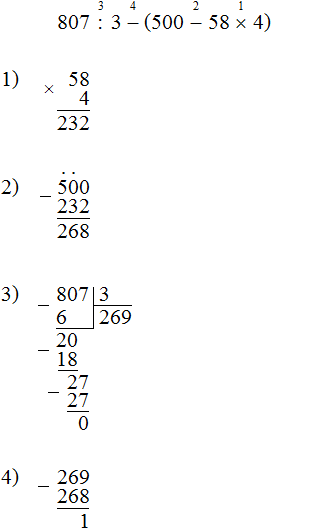
Дополнительные примеры
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Вычисляем:
1) 10 + 15 = 25
2) 25 – 6 = 19
3) 19 – 8 = 11
Полностью пример записываем так:
10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Вычисляем:
1) 15 : 5 = 3
2) 3 • 4 = 12
3) 12 : 6 = 2
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 – 5 = 5
4) 5 + 48 = 53
Полностью пример записываем так:
10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например, 
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

1) 25 – 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53
Полностью пример записываем так:
(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например, 
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Правила действий с отрицательными и положительными числами
Абсолютной величиной (или абсолютным значением) отрицательного числа называется
положительное число, получаемое от перемены его знака (-) на обратный (+). Абсолютная
величина -5 есть +5, т. е. 5. Абсолютной величиной положительного числа (а также числа ) называется само это число.
Знак абсолютной величины — две прямые черты, в которые заключается число, абсолютная величина которого берется. Например,
|-5| = 5,
|+5| = 5,
| 0 | = 0.
Сложение чисел с одинаковым знаком
сложении
Примеры.
(+8) + (+11) = 19;
(-7) + (-3) = -10.
б) При сложении двух чисел с разными знаками из абсолютной величины одного из них вычитается абсолютная величина другого (меньшая из большей) а ставится знак того числа, у которого абсолютная величина больше.
Примеры.
(-3) + (+12) = 9;
(-3) + (+1) = -2.
Вычитание (сложение) чисел с разными знаками
Вычитание
Примеры.
(+7) — (+4) = (+7) + (-4) = 3;
(+7) — (-4) = (+7) + (+4) = 11;
(-7) — (-4) = (-7) + (+4) = -3;
(-4) — (-4) = (-4) + (+4) = 0;
Замечание. При выполнении сложения и вычитания, особенно когда имеем дело с несколькими числами, лучше всего поступать так: 1) освободить все числа от скобок, при этом перед числом поставить знак « + », если прежний знак перед скобкой был одинаков со знаком в скобке, и « — », если он был противоположен знаку в скобке; 2) сложить абсолютные величины всех чисел, имеющих теперь слева знак +; 3) сложить абсолютные величины всех чисел, имеющих теперь слева знак -; 4) из большей суммы вычесть меньшую и поставить знак, соответствующий большей сумме.
Пример.
(-30) — (-17) + (-6) — (+12) + (+2);
(-30) — (-17) + (-6) — (+12) + (+2) = -30 + 17 — 6 — 12 + 2;
17 + 2 = 19;
30 + 6 + 12 = 48;
48 — 19 = 29.
Результат есть отрицательное число -29, так как большая сумма (48) получилась от сложения абсолютных величин тех чисел,
перед которыми стоили минусы в выражении
-30 + 17 – 6 -12 + 2.
На это последнее выражение можно смотреть и как на сумму чисел -30, +17, -6, -12, +2, и как на результат последовательного прибавления к числу -30 числа 17, затем вычитания числа 6, затем вычитания 12 и, наконец, прибавления 2. Вообще на выражение а — b + с — d и т. д. можно смотреть и как на сумму чисел (+а), (-b), (+с), (-d), и как на результат таких последовательных действий:
вычитания из (+а) числа (+b) , прибавления ( +c), вычитании ( +d) и т. д.
Умножение чисел с разными знаками
умножении
Схема (правило знаков при умножении):
|
+ |
* |
+ |
= |
+ |
|
+ |
* |
— |
= |
— |
|
— |
* |
+ |
= |
— |
|
— |
* |
— |
= |
+ |
Примеры.
( + 2,4) * (-5) = -12;
(-2,4) * (-5) = 12;
(-8,2) * (+2) = -16,4.
Примеры.
(+1/3) * (+2) * (-6) * (-7) * (-1/2) = -14 (три отрицательных сомножителя);
(-1/3) * (+2) * (-3) * (+7) * (+1/2) = 7 (два отрицательных сомножителя).
делении
Примеры.
(-6) : (+3) = -2;
(+8) : (-2) = -4;
(-12) : (-12) = + 1.
Главные правила по теме
Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:
2 + х = 5.
Аналогично:
8 : 2 = у × 2 = 8.
В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:
5 × 4 = 4 × 5.
При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.
Примеры решения задач
Пример 1
Задача
Решить уравнение , где – действительные числа.
Решение
Из уравнения комплексных чисел получается: , . Решая эту систему, у нас получается , .
Ответ
, .
Рассмотрим на примере сложение и вычитание комплексных чисел.
Пример 2
Задача
Решить уравнение:
Решение
Согласно формуле на сложение и отнимание комплексных чисел – .
Ответ
Рассмотрим на примере умножение комплексных чисел.
Пример 3
Задача
Найти произведение комплексных чисел и
Решение
Ответ
Делить комплексные числа необходимо исключительно ориентируясь на формулу. Покажем на примере, как находить частное.
Пример 4
Задача
Найти частное:
Решение
.
Ответ
.
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например, 
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

Полностью пример записываем так:
(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например, 
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Сложение двоичных чисел
Правила сложения двоичных чисел похожи на привычные нам: сложение происходит поразрядно справа налево, при этом важно помнить о переносе чисел в новый разряд. В десятичной системе у нас всего 10 цифр: от 0 до 9
Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10
В десятичной системе у нас всего 10 цифр: от 0 до 9. Когда мы складываем 1 и 9, у нас получается переполнение, так как больше 9 в одном разряде нельзя записать. Поэтому мы переносим единицу в следующий, получаем 10.
Двоичная система работает аналогично: чтобы понять, как складывать числа, нужно помнить об этом переполнении. Всего в двоичной системе две цифры — 0 и 1. Если сложить 1 и 1, мы получим переполнение, а значит, единица пойдёт в следующий разряд, результатом станет 10 (только не «десять», а «один-ноль»).
Если представить правила сложения двоичных чисел в общем виде, получим такую таблицу:
Изображение: Skillbox Media
Но лучше разобраться на примерах.
Пример 1. Давайте сложим 1100 и 101.
Изображение: Skillbox Media
Рассмотрим пример подробнее. Как мы уже упоминали ранее, сложение происходит справа налево. Разряды считаются тоже справа налево:
- Первый: 0 + 1 = 1.
- Второй: 0 + 0 = 0.
- Третий: 1 + 1 = 10 — переполнение, единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 10 — добавляем единицу из прошлого разряда, получаем переполнение, единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1 — единица пришла из предыдущего разряда.
Пример 2. Сложим 1111 и 111.
Изображение: Skillbox Media
Теперь поразрядно:
- Первый: 1 + 1 = 0 — единица переходит в следующий разряд.
- Второй: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Третий: 1 + 1 + 1 = 1 — единица переходит в следующий разряд.
- Четвёртый: 1 + 0 + 1 = 0 — единица переходит в следующий разряд.
- Пятый: 0 + 0 + 1 = 1.
Вроде бы пока несложно. Так что попробуйте сами сложить 1101 и 1011, чтобы закрепить знания.
2.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее
громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина.
Однако, чтобы профессионально использовать компьютер, следует научиться понимать
слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют
соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше
разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и
четвертая степени числа 2).
| Чтобы перевести восьмеричное (шестнадцатеричное) число в двоичную систему, нужно заменить каждую цифру восьмеричного (шестнадцатеричного) числа соответствующим трехразрядным (четырехразрядным) двоичным числом. Затем необходимо удалить крайние нули слева, а при наличии точки — и крайние нули справа. |
Например:

| Чтобы перевести двоичное число в восьмеричную (шестнадцатеричную) систему счисления нужно двигаясь от точки влево, а затем вправо, разбить двоичное число на группы по три (четыре) разряда, дополняя, при необходимости, нулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов следует заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,
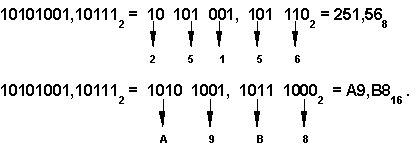
Свойства вычитания
1. Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
2. Скобки в выражении (a − b) − c не имеют значения и их можно опустить.
3. Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
4. Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть само число, то получится нуль.
































