Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками
, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2
.
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3
. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1
. Переходим ко второму выражению в скобках 6−4
. Здесь лишь одно действие – вычитание, выполняем его 6−4=2
.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2
. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6
. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6
.
Ответ:
5+(7−2·3)·(6−4):2=6
.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3))
.
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3)
. Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5
. Подставив найденное значение, получаем 3+1+4·5
. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24
. Исходное значение, после подстановки этого значения, принимает вид 4+24
, и остается лишь закончить выполнение действий: 4+24=28
.
Ответ:
4+(3+1+4·(2+3))=28
.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1
. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1
, то после этого исходное выражение примет вид (4+(4+1)−1)−1
. Опять выполняем действие во внутренних скобках, так как 4+1=5
, то приходим к следующему выражению (4+5−1)−1
. Опять выполняем действия в скобках: 4+5−1=8
, при этом приходим к разности 8−1
, которая равна 7
.
Как раскрыть 3 скобки
Бывают уравнения, в которых перемножаются сразу 3 скобки. В таком случае нужно сначала перемножить между собой слагаемые первых двух скобок, и затем сумму этого перемножения умножить на слагаемые третьей скобки. Пример:
(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + ![]() * (5 — 6) = — 21.
* (5 — 6) = — 21.
Данные правила раскрытия скобок одинаково распространяются для решения как линейных, так и тригонометрических уравнений.
«Раскрытие скобок» — Учебник по математике 6 класс (Виленкин)
Краткое описание:
В этом разделе Вы будете учиться раскрывать скобки в примерах. Для чего это нужно? Все для того же, что и раньше – чтобы Вам было легшее и проще считать, чтобы допускать меньше ошибок, а в идеале (мечта Вашего учителя математики) для того, чтобы вообще все решать без ошибок.
Вы уже знаете, что скобки в математической записи ставятся, если подряд идут два математических знака, если мы хотим показать объединение чисел, их перегруппировку. Раскрыть скобки означает избавиться от лишних знаков. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. А помните распределительное свойство умножения относительно сложения? Ведь в том примере мы также избавлялись от скобок для упрощения вычислений. Названное свойство умножения также можно применять для четырех, трех, пяти и более слагаемых. Для примера: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы заметили, что при раскрытии скобок числа, находящиеся в них не меняют знака, если стоящее перед скобками число положительное? Ведь пятнадцать – положительное число. А если решить такой пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+(-120)+(-135)+(-90)=-45-120-135-90=-390. У нас перед скобками стояло отрицательное число минус пятнадцать, когда мы раскрыли скобки все числа стали менять свой знак на другой — противоположный – с плюса на минус.
Исходя из вышеуказанных примеров, можно озвучить два основных правила раскрытия скобок:
1. Если у Вас перед скобками стоит положительное число, то после раскрытия скобок все знаки чисел, стоявших в скобках, не изменяются, а остаются точно такими же как и были.
2. Если у Вас перед скобками стоит отрицательное число, то после раскрытия скобок знак минуса больше не пишется, а знаки всех абсолютно чисел, стоявших в скобках, резко меняются на противоположные.
Для примера: (13+8)+(9-8)=13+8+9-8=22; (13+8)-(9-8)=13+8-9+8=20. Немного усложним наши примеры: (13+8)+2(9-8)=13+8+2*9-2*8=21+18-16=23. Вы заметили, что раскрывая вторые скобки, мы умножали на 2, но знаки оставались теми же как и были. А вот такой пример: (3+8)-2*(9-8)=3+8-2*9+2*8=11-18+16=9, в этом примере число два — отрицательное, оно перед скобками стоит со знаком минус, поэтому раскрывая их, мы меняли знаки чисел на противоположные (девять было с плюсом, стало с минусом, восемь было с минусом, стало с плюсом).
Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов.
Приведем примеры таких выражений:
\(5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\(xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)
Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам,
считая одночлен многочленом, состоящим из одного члена.
Например, многочлен
\(8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.
Представим все слагаемые в виде одночленов стандартного вида:
\(8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\(= 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)
Приведем в полученном многочлене подобные члены:
\(8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных.
Такие многочлены называют многочленами стандартного вида
.
За степень многочлена
стандартного вида принимают наибольшую из степеней его членов.
Так, двучлен \(12a^2b — 7b \) имеет третью степень, а трехчлен \(2b^2 -7b + 6 \) — вторую.
Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени.
Например:
\(5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)
Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.
Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это
преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:
Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.
Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.
Правила раскрытия скобок с произведением двух чисел
Наиболее типичный случай – когда x и y – это две положительные цифры. В таком случае если мы берем две отрицательных цифры, то их произведение будет выглядеть так:
(-x)*(-y)=(x*y)
Если две цифры имеют противоположные знаки, то выражение преобразование произведения будет выглядеть так:
(-x)*(y) или (x)*(-y) = (-x*y)
Умножение двух отрицательных чисел дает в итоге положительное, а произведение плюса на минус или минуса на плюс дает минус.
Если речь идет о первой части приведенного примера, то будем использовать правило произведения двух отрицательных множителей. Во втором случае применено правило произведения цифр с разными знаками.
Примеры
Возьмем произведение двух отрицательных цифр -5 и -3/4. Пример записываем следующим образом:
\[(-5*-3/4)=(5*3/4)=5*3/4.\]
Когда перед нами два простых отрицательных числа, произведение будет таким:
\
Знаки при раскрытии скобок играют ключевую роль независимо от того, приходится умножать, отнимать или слагать.
Пример произведения чисел с разными знаками:
\
Если нам нужно разделить, то предварительно потребуется избавиться от скобок:
\[(-6)/(3)=-6/3\]
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок
:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6
.
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7
отнимаем 3
, получаем 4
, после чего к полученной разности 4
прибавляем 6
, получаем 10
.
Кратко решение можно записать так: 7−3+6=4+6=10
.
Ответ:
7−3+6=10
.
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3
.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6
делим на 2
, это частное умножаем на 8
, наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2
.
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5
умножаем на 6
, получаем 30
, это число делим на 3
, получаем 10
. Теперь 4
делим на 2
, получаем 2
. Подставляем в исходное выражение вместо 5·6:3
найденное значение 10
, а вместо 4:2
— значение 2
, имеем 17−5·6:3−2+4:2=17−10−2+2
.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7
.
Ответ:
17−5·6:3−2+4:2=7
.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Раскрытие скобок как ключевой шаг в решении математических и программистских задач
Раскрытие скобок является одной из основных операций в математике и программировании. Этот шаг позволяет разобрать выражение на составные части и определить порядок выполнения операций.
В математике раскрытие скобок позволяет упростить выражение, применяя правила алгебры. Например, внутри скобок можно выполнить операции над слагаемыми или множителями, затем можно сложить или умножить результаты.
В программировании раскрытие скобок также является важным шагом для понимания логики исполнения программы. Как и в математике, оно позволяет разобрать программный код на отдельные операции и определить порядок их выполнения
Это особенно важно в условных конструкциях, циклах и арифметических выражениях
Для более наглядного представления раскрытия скобок в математике и программировании обычно применяются специальные символы и правила. Например, в математике часто используются круглые скобки (), квадратные скобки [], фигурные скобки {}, а также операторы умножения *, деления /, сложения + и вычитания -.
При выполнении раскрытия скобок в математике и программировании следует придерживаться определенных правил и приоритетов операций. Обычно сначала выполняются операции внутри самых вложенных скобок, затем внешних и так далее. В программировании также могут применяться правила приоритета операций, где определенным операциям присваивается высший приоритет.
Раскрытие скобок является ключевым шагом при решении математических и программистских задач. Оно позволяет разобрать сложные выражения на более простые составляющие, что упрощает их анализ и решение
Важно уметь правильно раскрывать скобки и следовать правилам приоритета операций в процессе выполнения задач
Правило раскрытия скобок при вычитании
Если перед скобками стоит знак «–», то при их раскрытии следует знаки слагаемых поменять на противоположные.
A – (b + c) = a – b– c
A – (b – c) = a – b + c
A – (-b + c) = a + b – c
A – (-b – c) = a + b + c
Когда в скобках перед первым слагаемым знак отсутствует, то это означает, что оно положительное и при раскрытии скобок становится отрицательным.
Решение подобных примеров состоит из действий:
- раскрываются скобки; меняется знак каждого слагаемого на противоположный.
X – (y + z) = x – y – z;
M – (-n – p) = m + n + p;
Случаи, когда в выражении присутствуют сложение и вычитание скобок.
10a + (19b – 34c) – 50 – (m + n)
В данном примере скобки раскрываются по алгоритму:
- к первой скобке применяется правило сложения; вторая скобка раскрывается правилом вычитания.
10a + 19b – 34 c – 50 – m – n
Раскрытие скобок в сложных выражениях.
Сложное выражение — это выражение, в котором используются скобки и знаки деление/умножение.
Как выбрать правильный знак препинания в скобках
1. Запятая. Запятая поставляется в скобки, когда там перечисление элементов, как правило это места, описания, прилагательные. Пример: Взяли с собой квас (сырой, неароматный), шашлыки (мягкие, сочные) и овощи (свежие, хрустящие).
2. Тире. Тире помогает выделить поясняющую, разъясняющую информацию. Оно ставится после слова, которое разъясняется. Пример: Лето – это пора года, когда можно купаться в море.
3. Двоеточие. Двоеточие используется, когда объявляется заключение. Пример: Принимаются документы для участия в конкурсе (передача должна проходить на территории России).
4. Вопросительный знак. Вопросительный знак ставится в скобки, когда в предложении есть вопросительная интонация. Пример: Я нашел все нужные документы (где же они были?).
5. Восклицательный знак. Восклицательный знак ставится в скобки, когда в предложении выражен эмоциональный окрас. Пример: Она была настолько благодарна (о, Боже!), что пустила слезу.
- В иных случаях скобки могут быть использованы просто для выделения информации.
- Помните, что использование скобок должно быть максимально обоснованно и точно отражать задуманное значение.
- Следуйте правильной пунктуации и не перегружайте текст скобками.
Первое правило раскрытия скобок
Рассмотрим выражение:
8 + (−9 + 3)
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
| Первое правило раскрытия скобок
Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак. Формула раскрытия скобок (a − b) = a — b |
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
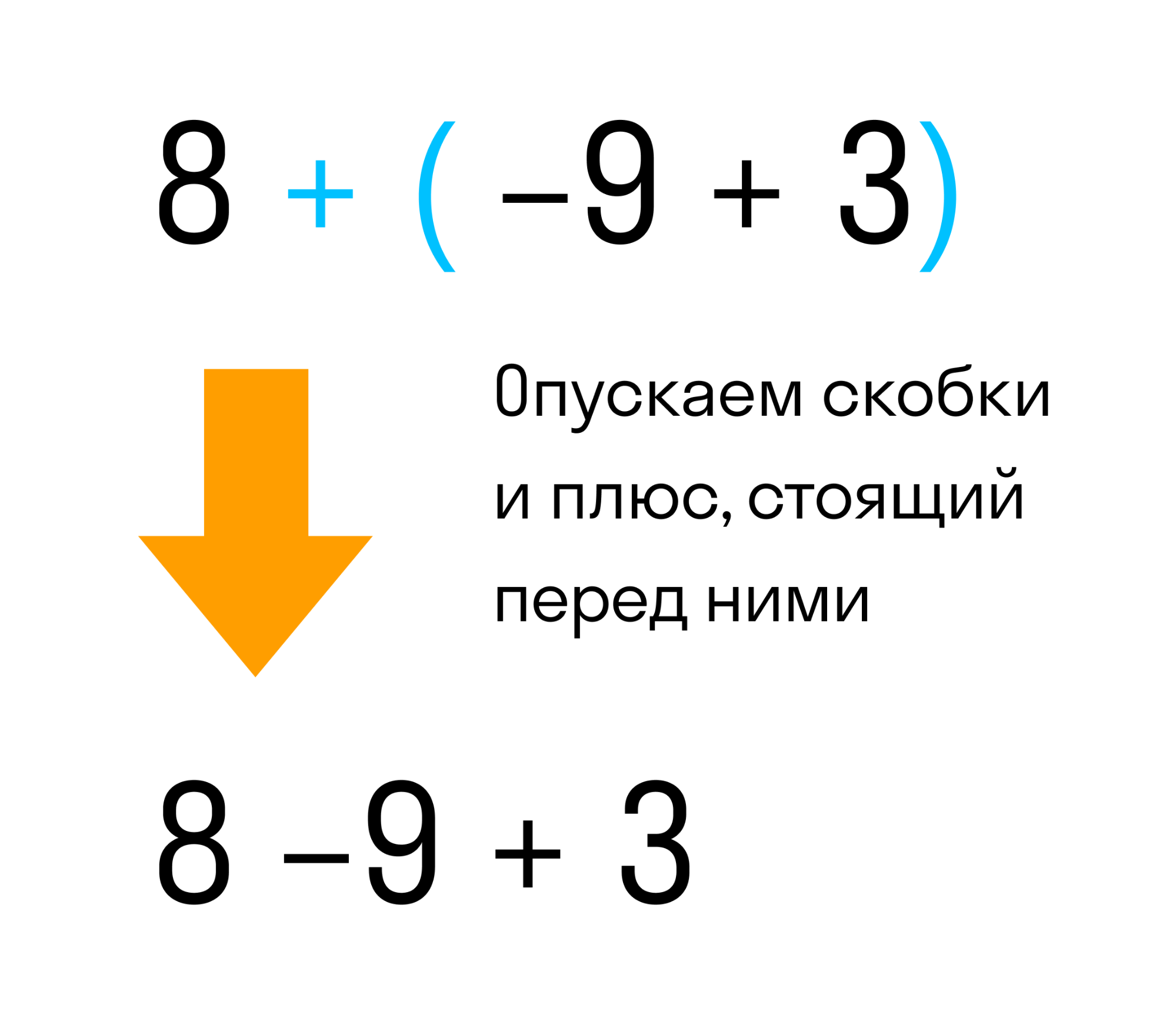
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
- 8 + (−9 + 3) = 2
- 8 − 9 + 3 = 2
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
- 8 + (−9 + 3) = 8 − 9 + 3
- 2 = 2
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Как рассуждаем:
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
8 + (−3 − 1) = 8 − 3 − 1
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Как рассуждаем:
Перед скобками стоит плюс, значит применим то же правило:
6 + (−2) = 6 − 2
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
2a + a — 5b + b = 2a + a + (-5b) + b = (2 + 1) * a + (-5 + 1) * b = 3a + (-4b)
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
3a + (−4b) = 3a − 4b
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
2 + (−3 + 1) + 3 + (−6)
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6
Пример 3.Раскрыть скобки 6 + (−3) + (−2)
Как рассуждаем:
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
6 + (−3) + (−2) = 6 − 3 − 2
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
1 + (2 + 3 − 4) = 1 + 2 + 3 − 4
Пример 4.Раскрыть скобки в выражении (−7)
Как рассуждаем:
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
(−7) = −7
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Как рассуждаем:
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
−
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Порядок вычисления простых выражений
Существует четкое правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются в порядке слева направо
- сначала выполняются умножение и деление, затем сложение и вычитание.
Из этого правила становится понятнее, какое действие выполняется первым. Универсального ответа нет, приходится разбирать каждый пример и выбирать решение самостоятельно.
| Что первично, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? Умножь и прибавь. |
Порядок действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято писать слева направо. А необходимость сначала умножать или делить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить расчет: 11 − 2 + 5.
Как мы решаем:
В нашем выражении нет умножения, деления и скобок, поэтому все операции выполняем слева направо. Сначала вычтите два из одиннадцати:
11 — 2 = 9
Затем прибавляем к результату пять, и в итоге получаем четырнадцать:
9 + 5 = 14
Вот полное решение: 11 − 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке следует производить вычисления в выражении: 10 : 2 × 7 : 5?
Как мы спорим:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление, а значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала делим десять на два:
10 : 2 = 5
Теперь умножьте результат на семь:
5 х 7 = 35
И полученное число делится на пять:
35 : 5 = 7
Запись всего решения выглядит так: 10 : 2 × 7 : 5 = 5 × 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока не известны новые знания, чтобы не путать последовательность действий при вычислении значения выражения, числа удобно ставить над знаками арифметических действий, соответствующих порядку их выполнения.
Например, в такой последовательности можно решить пример с действиями:
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать круглые скобки, обозначающие порядок выполнения математических операций, в этом случае действует правило:
Сначала выполните действия в скобках, при этом умножая и деля по порядку слева направо, а затем сложите и вычтите.
Выражения в скобках рассматриваются как компоненты исходного выражения. Они сохраняют уже известную нам последовательность действий.
Рассмотрим последовательность действий на примерах со скобками.
Пример 1 Вычислить: 10 + (8 − 2 × 3) × (12 −4): 2.
Как правильно решить пример:
Во-первых, давайте определимся с планом действий. Выражение содержит скобки, поэтому мы сначала выполним действия над выражениями, заключенными в эти скобки.
Что первично, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание.
Итак, мы определили первые три действия:
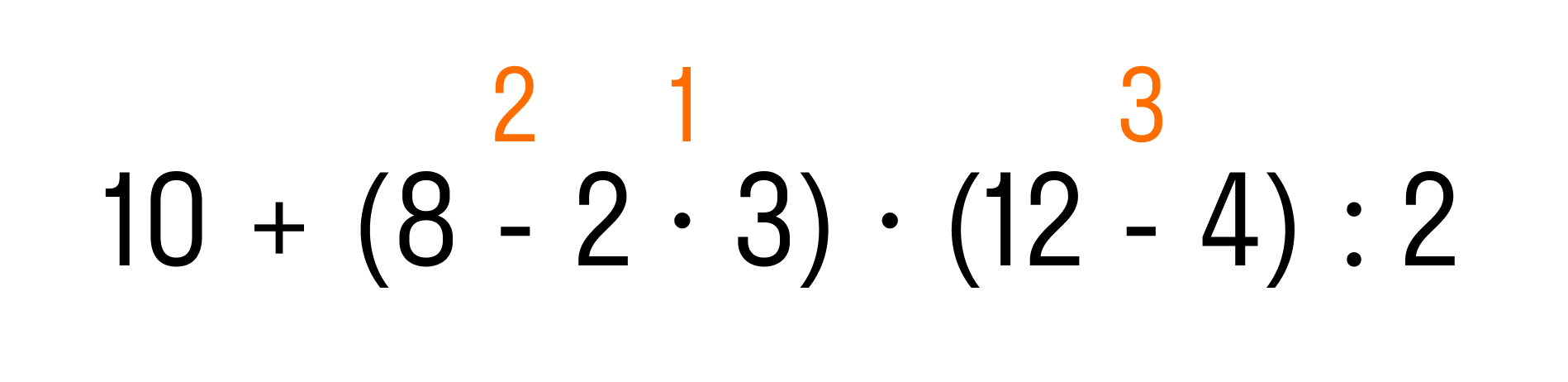
Когда все действия в скобках выполнены, по правилу надо выполнить умножение и деление, и, наконец, сложение. Теперь мы знаем, в каком порядке решать пример:
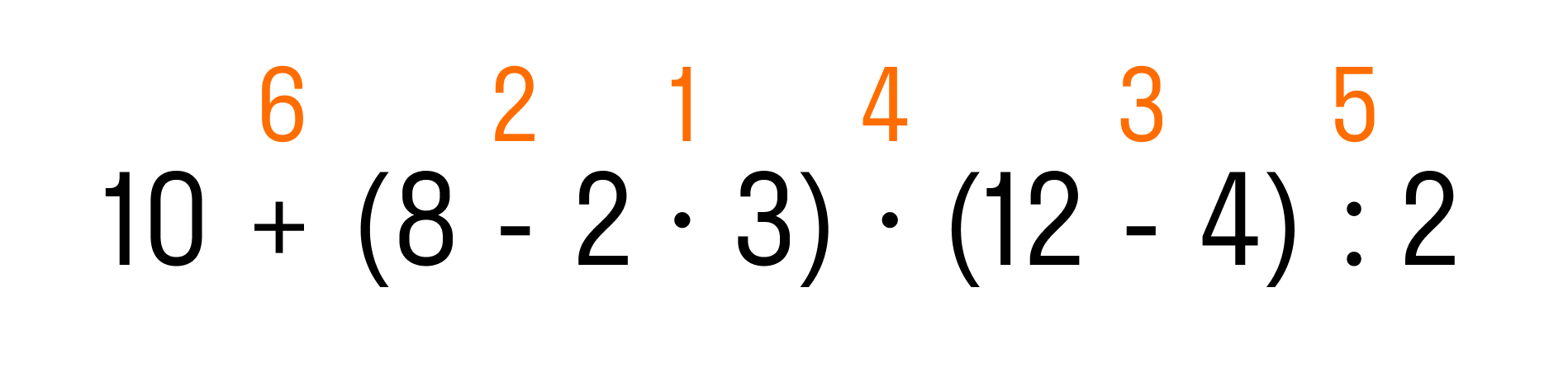
Осталось решить пример с действиями:
- 2 х 3 = 6
- 8 — 6 = 2
- 12 — 4 = 8
- 2 х 8 = 16
- 16 : 2 = 8
- 10 + 8 = 18
На этом все действия завершены.
Ответ: 10 + (7 — 2 × 3) × (12 — 4): 2 = 18.
Вы можете встретить выражения, содержащие скобки внутри скобок. Для их решения необходимо последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и переходить к внешним. Покажем пример.
Пример 2. Выполните действия над выражением: 9 + (5 + 1 + 4 × (2 + 3)).
Как мы решаем:
Сначала определим процедуру
Перед нами выражение со скобками. Это значит, что выполнение действий должно начинаться с выражения в скобках, то есть с 5+1+4×(2+3). Но это выражение также содержит круглые скобки, поэтому сначала начнем с действий внутри них:
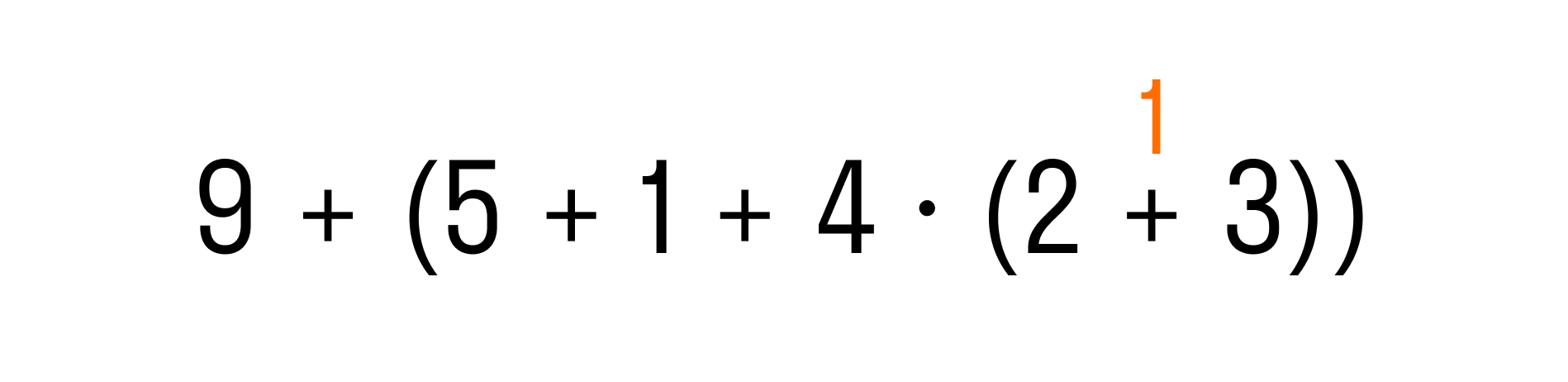
Теперь давайте перейдем к выражению во внешних скобках. Первой операцией по правилу будет умножение, а затем слева направо — две операции сложения:
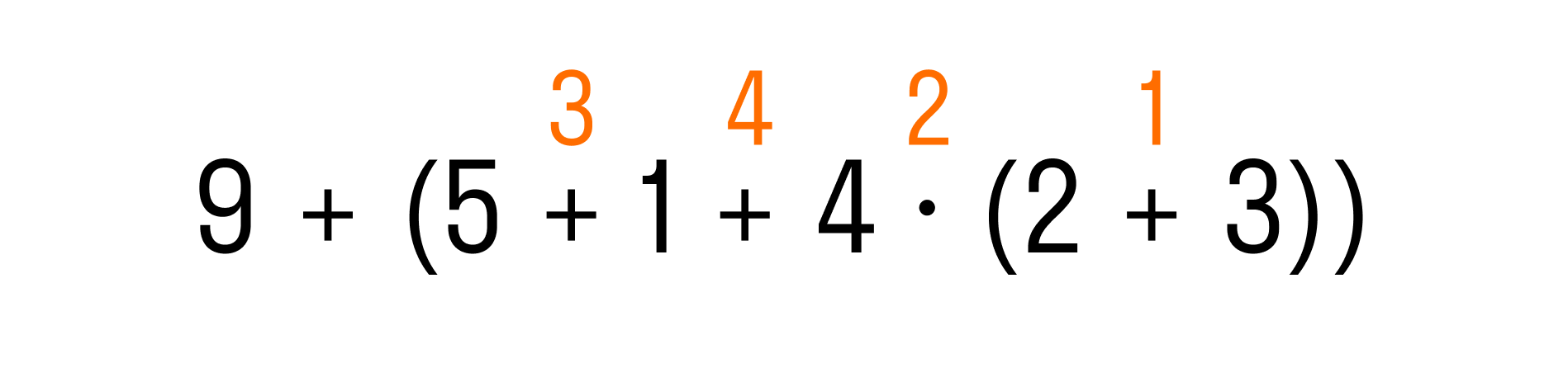
И последний шаг — выполнить сложение:
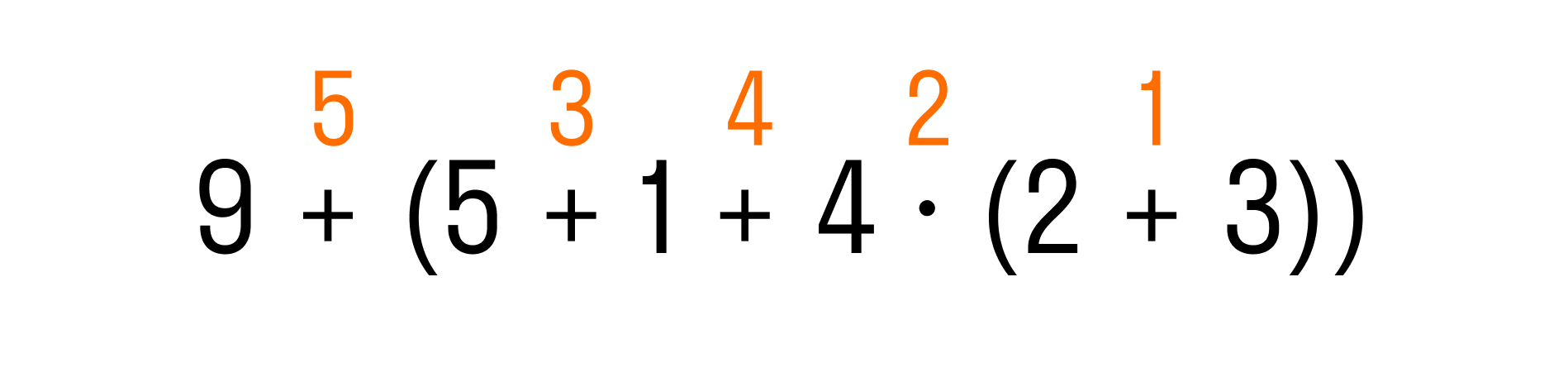
Рассчитываем по действиям:
- 2 + 3 = 5
- 4 х 5 = 20
- 5 + 1 = 6
- 6 + 20 = 26
- 9 + 26 = 35
Ответ: 4 + (3 + 1 + 4 × (2 + 3)) = 35.
Порядок действий без скобок
Установленный порядок арифметических операций без скобок:
- Если выражение содержит только операции сложения и вычитания, то они выполняются в следующем порядке — слева направо:
- Если выражение содержит только операции умножения и деления, то операции выполняются в следующем порядке — слева направо:
- Если выражение содержит как умножение и деление, так и сложение и вычитание, то сначала умножение и деление выполняются в их порядке (слева направо), а затем сложение и вычитание выполняются в их порядке (слева направо):
Порядок действий со скобками
Если выражение содержит скобки, сначала выполняются все действия внутри скобок, а затем выполняются все действия вне скобок.
В числовых выражениях со скобками порядок арифметических операций такой же, как и в выражениях без скобок.

Скобки используются для обозначения действий, которые должны быть выполнены в первую очередь. Скобки не влияют на порядок других действий в выражении, остальные действия выполняются в указанном порядке.
Раскрытие скобок при умножении
Действия по раскрытию скобок при умножении основаны на работе дистрибутивного или ассоциативного свойства умножения.
Применение того или иного свойства умножения зависит от действия в скобках. Если есть сложение или вычитание, работает распределительное свойство. При умножении или делении используется свойство ассоциативности.
1. Открывающие скобки в соответствии со свойством распределения.
При добавлении:
Правило 2
Чтобы умножить сумму на число, умножьте каждый член на это число и сложите результаты.
а ∙ (б + с) = аб + ас
(а + б) ∙ с = ас + Ьс
При вычитании:
Правило 3
Чтобы умножить разность на число, умножьте на это число сначала уменьшаемое, затем вычитаемое и из первого произведения вычтите второе.
а ∙ (б — в) = аб — ас
(а – б) ∙ с = ас – bc
Заметка 2
В математике для сокращения записей знак умножения не ставится перед числом и скобками.
Если общий множитель имеет отрицательное значение, все значения в скобках умножаются на (–1) и меняются местами:
-х(у + г) = -ху — хг
-х(у — г) = -ху + хг
2. Открывающие скобки по свойству ассоциативности:
Правило 4
Произведение трех и более факторов не изменится, если эту группу факторов заменить их произведением.
(а ∙ б) ∙ с = а ∙ б ∙ с
(б ∙ в ∙ г) ∙ а = б ∙ в ∙ д ∙ а
В случае, если умножение выполняется в скобках, раскрытие происходит как при сложении — скобки просто раскрываются и перемножаются все значения:
а ∙ (б ∙ с) = а ∙ б ∙ с
(б ∙ в) ∙ а = б ∙ с ∙ а
Заметка 3
При раскрытии скобок необходимо учитывать правило знака.
При умножении:
(+) · (+) = (+)
(+) · (-) = (-)
(-) · (+) = (-)
(-) · (-) = (+)
При совместном использовании:
(+) : (+) = (+)
(+) : (-) = (-)
(-) : (+) = (-)
(-) : (-) = (+)
При делении в скобках расширение происходит следующим образом:
Если общий множитель стоит перед скобками, то:
общий множитель умножается на первое число в скобках и делится на второе число:
а ⋅ (б : с) = а ⋅ б : с;
или общий множитель делится на второе число в скобках и умножается на первое число:
а ⋅ (б : с) = а : с ⋅ б.
Если общий множитель стоит после скобок, то:
общий множитель умножается на первое число в скобках и делится на второе:
(а : б) ⋅с = с ⋅ а : б;
общий множитель делится на второе число в скобках и умножается на первое:
(а : б) ⋅ с = с : б ⋅ а.
Скобка на скобку
Если вы хотите перемножить несколько скобок вместе, умножьте каждый элемент первой скобки на каждый член второй скобки:
(a + b) ⋅ (c — d) = a ⋅ (c — d) + b ⋅ (c — d) = ac — ad + bc — bd
Алгоритм действий при открытии скобки для скобки:
- Первая скобка раскрывается, каждое из слагаемых умножается на вторую скобку.
- Число умножается на скобки, даются аналогичные термины.
(5х + 7) ⋅ (10х — 2) =
5 х (10 х — 2) + 7 (10 х — 2) =
50x² — 10x + 70x — 14 =
50x² + 60 — 14
Скобка в скобке
В математике могут быть примеры, когда одни скобки заключаются в другие скобки.
Алгоритм действий такого типа примера:
- Каждая скобка раскрывается последовательно, начиная с внутренней.
- Скобки раскрываются в соответствии с принятыми правилами раскрытия скобок при сложении, вычитании, умножении и делении.
- Аналогичные термины даны для дальнейшего решения математического выражения или уравнения
8x + y(4 — (2x — y)) = 8x + y(4 — 2x + y) = 8x + 4y — 2xy + y²
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
![]()
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Раскрытие скобок и приведение подобных с примерами
Правила и закономерности раскрытия скобок зависят от того, какие числа или буквенные выражения заключены в скобках.
Одиночные цифры в скобках
В скобках могут быть размещены, как положительные, так и отрицательные числа. Начнем с положительных цифр. Для более детального и понятного разбора любое положительное число представим, как x. В таком случае можно заменить x на x, +(x) на +x, -(x) на –x.
Теперь возьмем реальный пример, где вместо x будут числовые значения. В соответствии с правилом, число 4 мы представим, как 4, выражение 2+(4) будет иметь вид 2+4 в связи с тем, что +(4) преобразуется в +4. Выражение 2+(-4) при раскрытии скобок будет выглядеть, как 2-4, так как +(-4) аналогично -4.
Если имеет дело с положительными цифрами, скобки можем просто опустить, так как они не имеют никакого смысла.
Из приведенных выше примеров вытекает первое правило:
Если перед скобками стоит знак плюс, то все числа, которые стоят внутри, сохраняют свой знак.
Формулы
Формула раскрытия скобок:
Если внутри расположено одиночное отрицательное число, то скобки раскрываются следующим образом:
+(-x) будет выглядеть, как –x
-(-x) будет выглядеть, как +x.
Отсюда вытекает еще одно правило раскрытия скобок.
Если впереди стоит знак минус, то все цифры внутри меняют знак на противоположный.
Формула будет выглядеть следующим образом.
Если перед скобками нет никакого знака, а внутри них отрицательное число, то скобки просто опускаются, и минус сохраняется.
Примеры:
- (-2) превратится в -2;
- (-1)+2 превратится в -1+2;
- 5+(-2) будет иметь вид 5-2;
- -(-1) превратится в +1.
Преобразование выражений, где есть произведение, происходит по-другому. Выражение 2*(-1) записать, как 2*-1 невозможно.
Согласно правилам разность b-a равна b+(-a). Исходя из этого, можно сформировать цепочку:
(b+(-a))+a=b+((-a)+a)=b+0=b, что будет вполне закономерно.
Эта цепочка доказывает, что b+(-a) это та же разность b-a.
Если опираться на основы вычитания и правила вычитания отрицательных чисел, то мы получим:
- -(-b)=b;
- b-(-a)=b+a.
Иногда встречаются выражения с большим количеством скобок. Раскрытие скобок и приведение подобных в таких примерах производится последовательно с учетом всех существующих правил.
Рассмотрим подробнее. Если взять выражение -(-((-(2)))), то избавляться от скобок стоит, начиная изнутри выражения:
-(-((-(2))))=-(-((-2)))=-(-(-2))=-(2)=-2.
Под буквами a и b можно понимать не только буквенные, но и любые численные выражения, которые имеют впереди знак плюс и не рассматриваются в контексте сложения или вычитания. В таких случаях правила действуют точно так же, как и в рассмотренных примерах.
К примеру, после раскрытия скобок выражение \ примет вид \. Как мы это сделали? Мы знаем, что \ есть \, а так как это выражение стоит вначале, то \ можно записать как \, \.
Памятка № 3, 4 по математике «Раскрытие скобок», «Положительные и отрицательные числа»
ПАМЯТКА 3
Раскрытие скобок
-
Если перед скобками стоит знак «+», то можно скобки опустить.
а + ( в — с ) = а + в — с
а + ( — в + с ) = а — в + с
-
Если перед скобками стоит знак «-», то все знаки в скобках меняем на противоположные.
в — ( а + с) = в — а — с
в — ( — а + с ) = в + а — с
с — ( в — а ) = с — в + а
с — (- в — а ) = с + в + а
-
Распределительное свойство
a ( b + c ) = ab + ac
a ( b — c ) = ab — ac
ПАМЯТКА 3
Раскрытие скобок
-
Если перед скобками стоит знак «+», то можно скобки опустить.
а + ( в — с ) = а + в — с
а + ( — в + с ) = а — в + с
-
Если перед скобками стоит знак «-», то все знаки в скобках меняем на противоположные.
в — ( а + с) = в — а — с
в — ( — а + с ) = в + а — с
с — ( в — а ) = с — в + а
с — (- в — а ) = с + в + а
-
Распределительное свойство
a ( b + c ) = ab + ac
a ( b — c ) = ab — ac
ПАМЯТКА 4
Сложение, вычитание, умножение и деление положительных и отрицательных чисел
-
Чтобы сложить два отрицательных числа, надо: 1) сложить их модули; 2) поставить перед полученным числом знак «-»
— 3 + ( — 2 ) = — 5
-
Чтобы сложить два числа с разными знаками, надо: 1) из большего модуля слагаемых вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
7 + ( — 2) = + ( 7 — 2) = 5; 5 + ( — 8 ) = — ( 8 — 5) = — 3;
— 3 + 9 = 9 — 3 = 6; — 6 + 4 = — ( 6 — 4) = — 2.
-
Чтобы вычесть два отрицательных числа, надо: 1) сложить их модули; 2) поставить перед полученным числом знак «-»
— 4 — 2 = — 6
-
При умножении (делении) чисел с разными знаками, надо перемножить (разделить) модули этих чисел и поставить перед полученным числом знак «-»
— 2 * 3 = — 6; 10 : ( — 2) = — 5;
4 * ( — 2) = — 8; — 9 : 3 = — 3
-
При умножении (делении) двух отрицательных чисел, надо перемножить (разделить) модули этих чисел
— 4 * ( — 3) = 12; — 15 : ( — 5) = 3






























