Таблица степеней

Таблица степеней

• Возведение в степень: определение
• Свойства степеней
  • Произведение степеней
  • Частное степеней
  • Возведение степени в степень
  • Степень произведения
  • Степень частного
• Виды таблиц
  • Таблица степеней натуральных чисел
  • Таблица отрицательных степеней
  • Таблица степеней двузначных чисел
• Степени от 1 до 10: пример
• Квадраты чисел до 100: пример

Возведение в степень: определение

Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.

Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:

4 3 , где 4 — это основание, а 3 — показатель. Также 4 3 = 4·4·4 = 64

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основные правила выполнения данных вычислений:

• итог возведения отрицательного основания в четную степень — положительный;
• итог возведения отрицательного основания в нечетную — отрицательный;
• итог возведения положительного основания в любую — положительный;
• любое основание с показателем один равно себе;
• ноль при любом возведении в результате дает ноль;
• единица с любым показателем равна единице;
• любое основание с показателем ноль равно единице.

Таблица представляет собой ряд чисел, возведенных в определенные степени.

Свойства степеней

a, b — любое рациональное число, n, m — любое натуральное

Частное степеней

Под выполнением данной операции понимается то, что одинаковое основание остается без изменений, а из показателя делимого вычитают показатель делителя.

Степень произведения

Для выполнения этого арифметического действия каждый из множителей возводится в степень, после чего полученные результаты перемножаются.

(left(acdot bright)^n=a^ncdot b^n)

Степень частного

Чтобы выполнить данную арифметическую операцию, следует возвести в степень делимое и делитель, а затем первый результат разделить на второй.

Виды таблиц

Таблица степеней натуральных чисел

Натуральными являются те числа, которые получаются при счете предметов. Наименьшее — один, наибольшего не существует.

Чтобы вычислить результат возведения, нужно основание умножить само на себя столько раз, сколько указано в показателе. То есть основание а с показателем n значит, что а нужно умножить на себя n раз.

Таблица для чисел от одного до десяти:

Таблица отрицательных степеней

Деление является обратной операцией умножению. Отрицательный показатель указывает на то, сколько раз необходимо разделить число. Легче всего представить в виде десятичной дроби:

Для вычисления (а^) нужно:

1. Возвести а в степень n.
2. Затем разделить единицу на полученный результат, то есть (frac) .

Пример таблицы для двойки:

Таблица степеней

Возведение в степень — бинарная операция, происходящая из сокращения для множественного умножения числа на самого себя. Обозначение: ab называется степенью с основанием a и показателем b. Логарифм — обратная к возведению в степень функция.

Ниже представлена таблица степеней от 1 до 10.

	1n	2n	3n	4n	5n	6n	7n	8n	9n	10n
1	1	2	3	4	5	6	7	8	9	10

2
1
4
9
16
25
36
49
64
81
100
3
1
8
27
64
125
216
343
512
729
1000
4
1
16
81
256
625
1296
2401
4096
6561
10000
5
1
32
243
1024
3125
7776
16807
32768
59049
100000
6
1
64
729
4096
15625
46656
117649
262144
531441
1000000
7
1
128
2187
16384
78125
279936
823543
2097152
4782969
10000000
8
1
256
6561
65536
390625
1679616
5764801
16777216
43046721
100000000
9
1
512
19683
262144
1953125
10077696
40353607
134217728
387420489
1000000000
10
1
1024
59049
1048576
9765625
60466176
282475249
1073741824
3486784401
10000000000

Другие заметки по алгебре и геометрии

Виды таблиц

Таблица степеней натуральных чисел

Натуральными являются те числа, которые получаются при счете предметов. Наименьшее — один, наибольшего не существует.

Чтобы вычислить результат возведения, нужно основание умножить само на себя столько раз, сколько указано в показателе. То есть основание а с показателем n значит, что а нужно умножить на себя n раз.

аn = а·а·…·а

Таблица для чисел от одного до десяти:

Таблица отрицательных степеней

Деление является обратной операцией умножению. Отрицательный показатель указывает на то, сколько раз необходимо разделить число. Легче всего представить в виде десятичной дроби:

\(а^{-n} = \frac{1}{а*а*\dots*а}\)

Для вычисления \(а^{-n}\) нужно:

1. Возвести а в степень n.
2. Затем разделить единицу на полученный результат, то есть \(\frac{1}{a^n}\).

Пример таблицы для двойки:

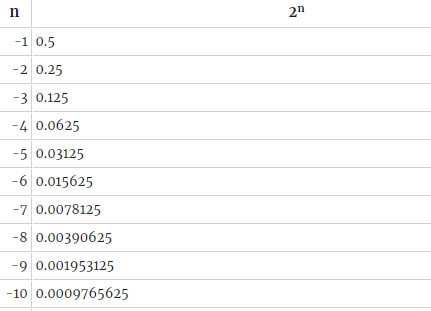
Таблица последовательных степеней числа 2.

      Число 2 в нулевой степени. Начинается таблица с нулевой степени числа два. Как известно, любое число в нулевой степени равняется единице. Поэтому два в нулевой степени равняется единице.

      Число 2 в первой степени. Если любое число возвести в первую степень, это число останется неизменным. Наша двойка в первой степени, соответственно, равняется двум. Если вы совершенно случайно повстречали число в первой степени, главное — не паникуйте. Никакой угрозы для ваших умственных способностей эта комбинация цифр не представляет. Любое число в первой степени равняется точно такому же числу без всяких показателей степени. Просто в математике не принято возле каждого числа записывать показатель степени один.

      Знаменитое «дважды два равно четыре» — это душещипательный математический рассказ о приключениях двойки, попавшей во вторую степень. Как бы там ни было, и на какой бы язык не переводили эту романтическую историю чисел, два во второй степени всегда будет равняться четырем. Возведение любого числа во вторую степень означает, что это число умножается само на себя. На практике это выполняется довольно просто: возьмите число два и умножьте его на точно такое же число два. 2 х 2 = 4 В результате умножения получается число четыре.

      В третьей степени число два равняется восьми. В отличие от умножения два на три, когда в результате получается шесть. Число три в показателе степени говорит нам о том, что мы берем три двойки и перемножаем их между собой. Естественно, что между тремя цифрами мы можем поставить только два знака умножения. 2 х 2 х 2 = 8 Как видите, совершенно логично, что два в третьей степени равняется восьми, а не шести.

      Число 2 в четвертой степени равняется шестнадцати. Умножаем между собой четыре двойки. 2 х 2 х 2 х 2 = 16 Здесь мы попадаем в область двузначных результатов, когда одно число записывается двумя цифрами. Есть еще два показателя степени числа два, дающие двузначные результаты. Два в пятой степени равняется тридцать два и два в шестой степени равняется шестьдесят четыре.

      Трехзначные результаты дает возведение числа два в седьмую, восьмую и девятую степени. А вот число два в десятой степени равняется одной тысяче двадцати четырем, что перевод нас в четырехзначные результаты. Всю дальнейшую эволюцию степеней числа два и их результатов можно проследить по расположенной выше таблице степеней числа два.

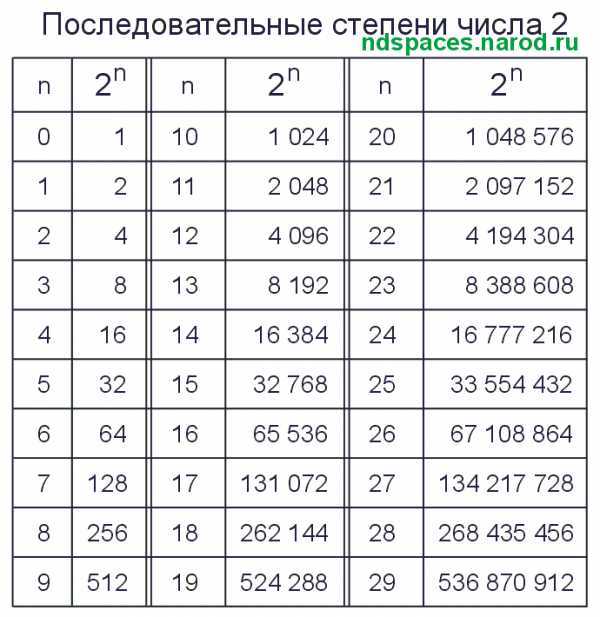
      Ещё одна таблица степеней числа 2 от 0 до 100. Таблица не самая правильная получилась, но компактная. Особенно полезной данная таблица будет для программистов.

      12 декабря 2009 года — 26 октября 2014 года.

Таблица степеней

Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.

Калькулятор степеней

\begin{align}
\end{align}

С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».

Таблица степеней от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
1n	1	1	1	1	1	1	1	1	1	1
2n	2	4	8	16	32	64	128	256	512	1024
3n	3	9	27	81	243	729	2187	6561	19683	59049
4n	4	16	64	256	1024	4096	16384	65536	262144	1048576
5n	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6n	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7n	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8n	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9n	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10n	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

Таблица степеней от 1 до 10

11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1	21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024	31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049	41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576	51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176	71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249	81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824	91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401	101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000

Теория

Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется — основанием степени, а количество операций умножения — показателем степени.

an = a×a … ×a

запись читается: «a» в степени «n».

«a» — основание степени

«n» — показатель степени

Пример:

Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.

• Нажмите на картинку чтобы посмотреть в увеличенном виде.
• Нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер. Изображение будет с высоким разрешением и в хорошем качестве.

Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней

Таблица степеней – перечень чисел от 1 до 10 возведенных в степень от
1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет
6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для
решения задач по
теории вероятности,
геометрии и математике! Также на сайте работает
форум, на котором Вы всегда можете
задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!

Таблица степеней 1 – 10

1 в степени:

11 = 1

12 = 1

13 = 1

14 = 1

15 = 1

16 = 1

17 = 1

18 = 1

19 = 1

110 = 1

2 в степени:

21 = 2

22 = 4

23 = 8

24 = 16

25 = 32

26 = 64

27 = 128

28 = 256

29 = 512

210 = 1024

3 в степени:

31 = 3

32 = 9

33 = 27

34 = 81

35 = 243

36 = 729

37 = 2187

38 = 6561

39 = 19683

310 = 59049

4 в степени:

41 = 4

42 = 16

43 = 64

44 = 256

45 = 1024

46 = 4096

47 = 16384

48 = 65536

49 = 262144

410 = 1048576

5 в степени:

51 = 5

52 = 25

53 = 125

54 = 625

55 = 3125

56 = 15625

57 = 78125

58 = 390625

59 = 1953125

510 = 9765625

6 в степени:

61 = 6

62 = 36

63 = 216

64 = 1296

65 = 7776

66 = 46656

67 = 279936

68 = 1679616

69 = 10077696

610 = 60466176

7 в степени:

71 = 7

72 = 49

73 = 343

74 = 2401

75 = 16807

76 = 117649

77 = 823543

78 = 5764801

79 = 40353607

710 = 282475249

8 в степени:

81 = 8

82 = 64

83 = 512

84 = 4096

85 = 32768

86 = 262144

87 = 2097152

88 = 16777216

89

Степень с натуральным показателем — что такое в алгебре

Степень в алгебре состоит из двух компонентов: основания и показателя. Основание степени — любое число. Показатель — число, которое показывает, сколько раз нужно умножить основание само на себя.

В математике — это степень, показатель которой является натуральным числом.

Вспомним, что натуральными называют все целые числа больше нуля. Так, числа 1; 365; 1890 будут натуральными, а числа 0; –9; 8,7 — нет.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Степень с натуральным показателем имеет вид выражения an, где a — основание, а n — любое натуральное число. Читается это выражение как «a в степени n». При этом a может быть любым.

Основные определения, свойства

Следуя из выражения an, дадим точное определение понятию степени с натуральным показателем.

Степенью числа a с натуральным показателем n называется произведение n одинаковых множителей, каждый из которых равен a.

Иногда возникают особые случаи решения данного выражения, а именно:

Степенью любого числа a с показателем 1 будет само а.

\(a^1=1;\)

Степенью любого числа с нулевым показателем будет ноль

\(a^0=0;\)

Ноль в любой степени будет равен нулю.

\(0^n=0;\)

Единица в любой степени будет равна единице.

\(1^n=1.\)

За исключением этих случаев, чтобы производить вычисления и различные действия со степенями, нужно знать основные свойства:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

\(a^n\times a^m=a^{(m+n)};\)

2. При делении степеней с одинаковыми основаниями основание остается прежним, а из показателя первой степени вычитается показатель второй.

\(\frac{a^n}{a^m}=a^{(n-m)};\)

3. При возведении степени в степень основание остается прежним, а показатели перемножаются.

 \(\left(a^n\right)^m=a^{(n\times m)};\)

     4. При возведении в степень произведения каждый множитель возводится в данную степень.

\({(a\times b)}^n=a^n\times b^n;\)

5. При возведении в степень дроби в данную степень возводится и числитель, и знаменатель.

\(\left(\frac ab\right)^n=\frac{a^n}{b^n}.\)

Свойства степеней

a, b — любое рациональное число, n, m — любое натуральное

Произведение степеней

Данное действие подразумевает то, что одинаковое основание остается без изменений, а показатели складываются.

\(a^n\cdot a^m=a^{n+m}\)

Частное степеней

Под выполнением данной операции понимается то, что одинаковое основание остается без изменений, а из показателя делимого вычитают показатель делителя.

\(\frac{a^m}{a^n}=a^{m-n}\)

Возведение степени в степень

Для вычисления результата этой операции основание остается без изменения, а показатели перемножаются.

\(\left(a^m\right)^n=a^{m\cdot n}\)

Степень произведения

Для выполнения этого арифметического действия каждый из множителей возводится в степень, после чего полученные результаты перемножаются.

\(\left(a\cdot b\right)^n=a^n\cdot b^n\)

Степень частного

Чтобы выполнить данную арифметическую операцию, следует возвести в степень делимое и делитель, а затем первый результат разделить на второй.

\(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\)

Таблица, формулы

В процессе решения примеров часто встречается необходимость возведения числа в степень. Упростить данную задачу можно, если иметь под рукой таблицу:

Основные свойства степеней:

Произведение:

Деление:

Возведение степени в степень:

В зависимости от знака числа определяются знаки их степеней:

1. Результатом возведения отрицательного числа в четную степень станет положительное число.
2. Если отрицательное число возвести в нечетную степень, получится отрицательное число.
3. Независимо от вида степени, возведенное в нее положительное число даст в результате положительное число.
4. Значение степени нуля является нулевым.

При решении задач на степени с целым показателем полезно использовать следующие свойства:

1. Выражение  не имеет смысла при . При k > 0 получаем .
2. Какое-либо число, возведенное в степень 0, равно 1: .
3. Число, отличное от нуля, в отрицательной степени является обратным аналогичному числу в положительной степени:

Таблица степеней по алгебре: числа в квадрате

Расписать абсолютно каждое число и найти его значение во всех степенях — невозможно. В сложных примерах рекомендуется использовать онлайн калькуляторы. Мы же рассматриваем наиболее примитивные и распространенные случаи. В основном, в средней школе (вплоть до 11 класса) рассматриваются примеры с перемножением незначительное количество раз. Часто используется квадрат (a2). Некоторые числа мы уже возводили в него (от 1 до 25). Значения больших чисел же можно искать тут:

_{*Для лучшего понимания примеры подсвечены голубым.}

С левой стороны указаны десятки, а сверху — единицы. Т.е., для возведения в квадрат числа 24 ищем пересечение его десятка и единицы (2 — десяток, 4 — единица). Получаем показатель 576. Таким образом данная таблица степеней натуральных чисел может использоваться для возведения в квадрат цифр до 99.

Пример 3. Возводим большие значения в квадрат.

Задача. Найти 632.

Решение. В числе «63» 6 десятков и 3 единицы. Десятки у нас находятся с левой стороны, а единицы — в верхней строчке. Ищем нужные значения в таблице степеней по алгебре и находим число, находящееся на их пересечении.

Ответ. 3969.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Калькулятор степеней – возвести в степень онлайн

Калькулятор помогает быстро возвести число в степень онлайн. Основанием степени могут быть любые числа (как целые, так и вещественные). Показатель степени также может быть целым или вещественным, и также как положительным, так и отрицательным. Следует помнить, что для отрицательных чисел возведение в нецелую степень не определено и потому калькулятор сообщит об ошибке в случае, если вы всё же попытаетесь это выполнить.

Что такое натуральная степень числа?

Число называют -ой степенью числа , если равно числу , умноженному само на себя раз: – называется показателем степени, а число – основанием степени.

Как возвести число в натуральную степень?

Чтобы понять, как возводить различные числа в натуральные степени, рассмотрим несколько примеров:

Пример 1. Возвести число три в четвёртую степень. То есть необходимо вычислить 3

4Решение: как было сказано выше, = = .Ответ: .

Пример 2. Возвести число пять в пятую степень. То есть необходимо вычислить 55Решение: аналогично, = = .Ответ: .

Таким образом, чтобы возвести число в натуральную степень, достаточно всего лишь умножить его само на себя раз.

Что такое отрицательная степень числа?

-n

При этом отрицательная степень существует только для отличных от нуля чисел, так как в противном случае происходило бы деление на ноль.

Как возвести число в целую отрицательную степень?

Чтобы возвести отличное от нуля число в отрицательную степень, нужно вычислить значение этого числа в той же положительной степени и разделить единицу на полученный результат.

Пример 1. Возвести число два в минус четвёртую степень. То есть необходимо вычислить 2-4

Решение

Ответ: .

Числа. Степень числа.

Общеизвестный факт что сумму нескольких равных слагаемых можно найти с помощью умножения. Например : 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5 6 .

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5 6 и говорят «пять в шестой степени».

Выражение 5 6 – это степенью числа, где:

5 – основание степени;

6 – показатель степени.

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

В общем виде степень с основанием “a” и показателем “n” записывается так

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

Если основание степени «а» равно 1, то значение степени при любом натуральном n будет равно 1. Например, 1 5 =1, 1 256 =1

Если возвести число «а» возвести в первую степень, то получим само число a: a 1 = a

Если возвести любое число в нулевой степень, то в результате вычислений получим один . a 0 = 1

Особыми считают вторую и третью степень числа. Для них придумали названия: вторую степень называют квадратом числа, третью – кубом этого числа.

В степень можно возводить любое число – положительное, отрицательное или нуль. При этом не пользуются следующими правилами:

-при нахождении степени положительного числа получается положительное число.

-при вычислениях нуля в натуральной степени получаем ноль.

– при вычислении степени отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Если решить несколько примеров на вычисление степени отрицательных чисел, то получится, что если мы вычисляем нечётную степень отрицательного числа, то в результате будет число со знаком минус. Так как при умножении нечётного количество отрицательных сомножителей получаем отрицательное значение.

Если же мы рассчитываем четную степень для отрицательного числа, то в результате будет положительное число. Так как при умножении чётного количества отрицательных сомножителей получаем положительное значение.

Свойства степени с натуральным показателем.

Чтобы умножить степени с одинаковыми основаниями мы основания не меняем, а показатели степеней складываем:

например: 7 1.7 · 7 – 0.9 = 7 1.7+( – 0.9) = 7 1.7 – 0.9 = 7 0.8

Чтобы разделить степени с одинаковыми основаниями основание не меняем, а показатели степеней вычитаем:

например: 13 3.8 / 13 -0.2 = 13 (3.8 -0.2) = 13 3.6

При расчетах возведения степени в степень основание не меняем, а показатели степеней умножаем друг на друга.

например: (2 3 ) 2 = 2 3·2 = 2 6

Если необходимо рассчитать возведение в степень произведения, то в эту степень возводится каждый множитель

например:(2·3) 3 = 2 n · 3 m ,

При выполнении расчетов по возведению в степень дроби мы в данную степень возводим числитель и знаменатель дроби

например: (2 / 5) 3 = (2 / 5) · (2 / 5) · (2 / 5) = 2 3 / 5 3 .

Последовательность выполнения расчетов при работе с выражениями содержащими степень.

При выполнении расчетов выражений без скобок, но содержащих степени, в первую очередь производят возведение в степень, потом действия умножение и деление, и лишь потом операции сложения и вычитания.

Если необходимо вычислить выражение содержащие скобки, то сначала в указанном выше порядке делаем вычисления в скобках, а потом оставшиеся действия в том же порядке слева направо.

Очень широко в практических вычислениях для упрощения расчетов используют готовые таблицы степеней.

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1 Произведение степеней

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

• Упростить выражение. b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Представить в виде степени. 6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
• Представить в виде степени. (0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями. Оно не относится к их сложению

Нельзя заменять сумму (3 3 + 3 2 ) на 3 5 . Это понятно, если посчитать (3 3 + 3 2 ) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2 Частное степеней

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

m : a n =–>

a m

a n

= a m − n , где « a » — любое число, не равное нулю, а « m », « n » — любые натуральные числа такие, что « m > n ».

• Записать частное в виде степени (2b) 5 : (2b) 3 = (2b) 5 − 3 = (2b) 2
• Вычислить.
  

  11 3 · 4 2

  11 2 · 4

  = 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44

• Пример. Решить уравнение. Используем свойство частного степеней. 3 8 : t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение. 4 5m + 6 · 4 m + 2 : 4 4m + 3 = 4 5m + 6 + m + 2 : 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Пример. Найти значение выражения, используя свойства степени.

512 · 4

32

=

512 · 4

32

=

2 9 · 2 2

2 5

=

2 9 + 2

2 5

=

2 11

2 5

= 2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями. Нельзя заменять разность (4 3 −4 2 ) на 4 1

Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4

Нельзя заменять разность (4 3 −4 2 ) на 4 1 . Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3 Возведение степени в степень

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(a n ) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

• Пример. (a 4 ) 6 = a 4 · 6 = a 24
• Пример. Представить 3 20 в виде степени с основанием 3 2 .

По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:

Свойства 4 Степень произведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.

• Пример 1. (6 · a 2 · b 3 · c ) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2
• Пример 2. (−x 2 · y) 6 = ( (−1) 6 · x 2 · 6 · y 1 · 6 ) = x 12 · y 6

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке. (a n · b n )= (a · b) n

(a n · b n )= (a · b) n

То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

• Пример. Вычислить. 2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
• Пример. Вычислить. 0,5 16 · 2 16 = (0,5 · 2) 16 = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216

Пример возведения в степень десятичной дроби.

4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

Свойства 5 Степень частного (дроби)

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b) n = a n : b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

Пример. Представить выражение в виде частного степеней. (5 : 3) 12 = 5 12 : 3 12

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

📝Таблица чисел от 1 до 25 в степени от 1 до 10

При решении разных математических упражнений часто приходится заниматься возведением числа степень, в основном от 1 до 10. И для того, что бы быстрее находить эти значения и нами создана таблицу степеней по алгебре, которую я опубликую на этой странице.

Также у нас вы можете посмотреть таблицы квадратов и кубов.

Для начала рассмотрим числа от 1 до 6. Результаты здесь ещё не очень большие все из них вы можете проверить на обычном калькуляторе.

• 1 и 2 в степени от 1 до 10
  

  11= 112= 113= 114= 115= 116= 117= 118= 119= 1110= 1

  21= 222= 423= 824= 1625= 3226= 6427= 12828= 25629= 512210= 1 024

• 3 и 4 в степени от 1 до 10
  

  3 1 = 33 2 = 93 3 = 273 4 = 813 5 = 2433 6 = 7293 7 = 2 1873 8 = 6 5613 9 = 19 6833 10 = 59 049

  4 1 = 44 2 = 164 3 = 644 4 = 2564 5 = 1 0244 6 = 4 0964 7 = 16 3844 8 = 65 5364 9 = 262 1444 10 = 1 048 576

• 5 и 6 в степени от 1 до 10
  

  5 1 = 55 2 = 255 3 = 1255 4 = 6255 5 = 3 1255 6 = 15 6255 7 = 78 1255 8 = 390 6255 9 = 1 953 1255 10 = 9 765 625

  6 1 = 66 2 = 366 3 = 2166 4 = 1 2966 5 = 7 7766 6 = 46 6566 7 = 279 9366 8 = 1 679 6166 9 = 10 077 6966 10 = 60 466 176

• 7 и 8 в степени от 1 до 10
  

  7 1 = 77 2 = 497 3 = 3437 4 = 2 4017 5 = 16 8077 6 = 117 6497 7 = 823 5437 8 = 5 764 8017 9 = 40 353 6077 10 = 282 475 249

  8 1 = 88 2 = 648 3 = 5128 4 = 4 0968 5 = 32 7688 6 = 262 1448 7 = 2 097 1528 8 = 16 777 2168 9 = 134 217 7288 10 = 1 073 741 824

• 9 и 10 в степени от 1 до 10
  

  9 1 = 99 2 = 819 3 = 7299 4 = 6 5619 5 = 59 0499 6 = 531 4419 7 = 4 782 9699 8 = 43 046 7219 9 = 387 420 4899 10 = 3 486 784 401

  10 1 = 1010 2 = 10010 3 = 1 00010 4 = 10 00010 5 = 100 00010 6 = 1 000 00010 7 = 10 000 00010 8 = 100 000 00010 9 = 1 000 000 00010 10 = 10 000 000 000

• 11 и 12 в степени от 1 до 10
  

  11 1 = 1111 2 = 12111 3 = 1 33111 4 = 14 64111 5 = 161 05111 6 = 1 771 56111 7 = 19 487 17111 8 = 214 358 88111 9 = 2 357 947 69111 10 = 25 937 424 601

  12 1 = 1212 2 = 14412 3 = 1 72812 4 = 20 73612 5 = 248 83212 6 = 2 985 98412 7 = 35 831 80812 8 = 429 981 69612 9 = 5 159 780 35212 10 = 61 917 364 224

• 13 и 14 в степени от 1 до 10
  

  13 1 = 1313 2 = 16913 3 = 2 19713 4 = 28 56113 5 = 371 29313 6 = 4 826 80913 7 = 62 748 51713 8 = 815 730 72113 9 = 10 604 499 37313 10 = 137 858 491 849

  14 1 = 1414 2 = 19614 3 = 2 74414 4 = 38 41614 5 = 537 82414 6 = 7 529 53614 7 = 105 413 50414 8 = 1 475 789 05614 9 = 20 661 046 78414 10 = 289 254 654 976

• 15 и 16 в степени от 1 до 10
  

  15 1 = 1515 2 = 22515 3 = 3 37515 4 = 50 62515 5 = 759 37515 6 = 11 390 62515 7 = 170 859 37515 8 = 2 562 890 62515 9 = 38 443 359 37515 10 = 576 650 390 625

  16 1 = 1616 2 = 25616 3 = 4 09616 4 = 65 53616 5 = 1 048 57616 6 = 16 777 21616 7 = 268 435 45616 8 = 4 294 967 29616 9 = 68 719 476 73616 10 = 1 099 511 627 776

• 17 и 18 в степени от 1 до 10
  

  17 1 = 1717 2 = 28917 3 = 4 91317 4 = 83 52117 5 = 1 419 85717 6 = 24 137 56917 7 = 410 338 67317 8 = 6 975 757 44117 9 = 118 587 876 49717 10 = 2 015 993 900 449

  18 1 = 1818 2 = 32418 3 = 5 83218 4 = 104 97618 5 = 1 889 56818 6 = 34 012 22418 7 = 612 220 03218 8 = 11 019 960 57618 9 = 198 359 290 36818 10 = 3 570 467 226 624

• 19 и 20 в степени от 1 до 10
  

  19 1 = 1919 2 = 36119 3 = 6 85919 4 = 130 32119 5 = 2 476 09919 6 = 47 045 88119 7 = 893 871 73919 8 = 16 983 563 04119 9 = 322 687 697 77919 10 = 6 131 066 257 801

  20 1 = 2020 2 = 40020 3 = 8 00020 4 = 160 00020 5 = 3 200 00020 6 = 64 000 00020 7 = 1 280 000 00020 8 = 25 600 000 00020 9 = 512 000 000 00020 10 = 10 240 000 000 000

• 21 и 22 в степени от 1 до 10
  

  21 1 = 2121 2 = 44121 3 = 9 26121 4 = 194 48121 5 = 4 084 10121 6 = 85 766 12121 7 = 1 801 088 54121 8 = 37 822 859 36121 9 = 794 280 046 58121 10 = 16 679 880 978 201

  22 1 = 2222 2 = 48422 3 = 10 64822 4 = 234 25622 5 = 5 153 63222 6 = 113 379 90422 7 = 2 494 357 88822 8 = 54 875 873 53622 9 = 1 207 269 217 79222 10 = 26 559 922 791 424

• 23 и 24 в степени от 1 до 10
  

  23 1 = 2323 2 = 52923 3 = 12 16723 4 = 279 84123 5 = 6 436 34323 6 = 148 035 88923 7 = 3 404 825 44723 8 = 78 310 985 28123 9 = 1 801 152 661 46323 10 = 41 426 511 213 649

  24 1 = 2424 2 = 57624 3 = 13 82424 4 = 331 77624 5 = 7 962 62424 6 = 191 102 97624 7 = 4 586 471 42424 8 = 110 075 314 17624 9 = 2 641 807 540 22424 10 = 63 403 380 965 376

• 25 в степени от 1 до 10
  

  25 1 = 2525 2 = 62525 3 = 15 62525 4 = 390 62525 5 = 9 765 62525 6 = 244 140 62525 7 = 6 103 515 62525 8 = 152 587 890 62525 9 = 3 814 697 265 62525 10 = 95 367 431 640 625

Хочу напомнить:

Вот, например, в начале изучения компьютера мы рассматриваем двоичный код – то есть язык, на котором «разговаривает» компьютер. И там часто используются разные степени двойки, которые надо знать. От вы знаете, сколько будет два в восьмой?

Материалы по теме:

Поделиться с друзьями:

Как пользоваться таблицей степеней числа два ?

Первый столбец — это степень двойки
, который одновременно, обозначает число бит, которое представляет число.

Второй столбец — значение двойки в соответствующей степени (n)
.

Пример нахождения степени числа 2
. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени
(2 7
) — это 128

Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит
(в первом столбце).

Пример определения максимального целого числа без знака
. Если использовать данные из предыдущего примера, мы знаем, что 2 7 = 128
. Это верно, если мы хотим понять, какое количество чисел
, можно представить с помощью семи бит. Но, поскольку первое число — это ноль
, то максимальное число, которое можно представить с помощью семи бит 128 — 1 = 127
. Это и есть значение третьего столбца.

Таблица степеней 2 (двойки)

Приведенная таблица кроме степени двойки показывает максимальные числа, которые может хранить компьютер для заданного числа бит. Причем как для целых так и чисел со знаком.

Исторически сложилось, что компьютеры используют двоичную систему счисления, а, соответственно, и хранения данных. Таким образом, любое число можно представить как последовательность нулей и единиц (бит информации). Существует несколько способов представления чисел в виде двоичной последовательности. 

Рассмотрим наиболее простой из них — это целое положительное число. Тогда чем больше число нам нужно записать, тем более длинная последовательность бит нам необходима.

таблица степеней числа 2

Как пользоваться таблицей степеней числа два? 

Первый столбец — это

Второй столбец — значение двойки в соответствующей степени (n). 

Пример нахождения степени числа 2. Находим в первом столбце число 7. Смотрим по строке вправо и находим значение два в седьмой степени (27) — это 128

Третий столбец — максимальное число, которое можно представить с помощью заданного числа бит (в первом столбце). 

Пример определения максимального целого числа без знака. Если использовать данные из предыдущего примера, мы знаем, что 27 = 128. Это верно, если мы хотим понять, какое

первое число — это ноль

Степень двойки (n)

Значение степени двойки 2n

Максимальное число без знака, записанное с помощью n бит

Максимальное число со знаком,  записанное с помощью n бит

1
—
—

1
2
1
—

2
4
3
1

3
8
7
3

4
16
15
7

5
32
31
15

6
64
63
31

7
128
127
63

8
256
255
127

9
512
511
255

10
1 024
1 023
511

11
2 048
2 047
1023

12
40 96
4 095
2047

13
8 192
8 191
4095

14
16 384
16 383
8191

15
32 768
32 767
16383

16
65 536
65 535
32767

17
131 072
131 071
65 535

18
262 144
262 143
131 071

19
524 288
524 287
262 143

20
1 048 576

1 048 575
524 287
21
2 097 152
2 097 151
1 048 575

22
4 194 304
4 194 303
2 097 151

23
8 388 608
8 388 607
4 194 303

24
16 777 216
16 777 215
8 388 607

25
33 554 432
33 554 431
16 777 215

26
67 108 864

67 108 863
33 554 431

27
134 217 728
134 217 727
67 108 863

28
268 435 456
268 435 455
134 217 727

29
536 870 912
536 870 911
268 435 455

30
1 073 741 824
1 073 741 823
536 870 911

31
2 147 483 648
2 147 483 647
1 073 741 823

32

4 294 967 296
4 294 967 295
2 147 483 647

Необходимо принять во внимание, что не все числа в компьютере представлены таким образом. Существуют и другие способы представления данных

Например, если мы хотим записывать не только положительные, но и отрицательные числа, то нам потребуется еще один бит для хранения значения «плюс/минус». Таким образом, количество бит, предназначенных для хранения чисел у нас уменьшилось на один. Какое максимальное число может быть записано в виде целого числа со знаком можно посмотреть в четвертом столбце.

Для этого же самого примера

7