Действия с десятичными дробями
Одним из действий с десятичными дробями является сравнение, также определены четыре основных арифметических действия с десятичными дробями: сложение, вычитание, умножение и деление. Рассмотрим отдельно каждое из действий с десятичными дробями.
Сравнение десятичных дробей по сути базируется на сравнении обыкновенных дробей, отвечающих сравниваемым десятичным дробям. Однако перевод десятичных дробей в обыкновенные является достаточно трудоемким действием, да и бесконечные непериодические дроби не могут быть представлены в виде обыкновенной дроби, поэтому удобно использовать поразрядное сравнение десятичных дробей. Поразрядное сравнение десятичных дробей аналогично сравнению натуральных чисел. Для получения более детальной информации рекомендуем изучить материал статьи сравнение десятичных дробей, правила, примеры, решения.
Рассмотрим следующее действие с десятичными дробями – сложение десятичных дробей. Наиболее удобно сложение конечных десятичных дробей по правилу, аналогичному сложению столбиком натуральных чисел. Для сложения периодических десятичных дробей приходится их заменять обыкновенными дробями, после чего выполнять сложение обыкновенных дробей. Что касается сложения бесконечных непериодических десятичных дробей, то складываемые дроби обычно предварительно округляют (смотрите округление чисел), придерживаясь требуемой точности, после чего проводят сложение полученных после округления конечных десятичных дробей. Аналогично выполняют и другие действия с бесконечными непериодическими дробями. Далее смотрите статью сложение десятичных дробей, правила, примеры, решения.
Вычитание десятичных дробей представляет собой действие, обратное сложению. То есть, вычитание десятичных дробей – это нахождение числа, которое в сумме с вычитаемой десятичной дробью даст уменьшаемую десятичную дробь. Для дальнейшего изучения этого действия с десятичными дробями подходит статья вычитание десятичных дробей, правила, примеры, решения.
Переходим к следующему действию — умножению десятичных дробей. Умножение конечных десятичных дробей проводится аналогично вычитание десятичных дробей, правила, примеры, решенияумножению столбиком натуральных чисел. В случае периодических дробей умножение можно свести к умножению обыкновенных дробей. В свою очередь умножение бесконечных непериодических десятичных дробей после их округления сводится к умножению конечных десятичных дробей. Рекомендуем к дальнейшему изучению материал статьи умножение десятичных дробей, правила, примеры, решения.
Деление десятичных дробей представляет собой действие, обратное умножению. На практике, деление десятичных дробей сводится к делению десятичной дроби на натуральное число в столбик, которое аналогично делению в столбик натуральных чисел. Дальнейшая информация по теме собрана в статье деление десятичных дробей, правила, примеры, решения.
Слайды и текст этой презентации

История возникновения десятичных дробей

Зарождение десятичных дробей произошло в Китае Уже во II веке до н.э. там существовала десятичная система мер длины. Примерно в III веке н.э. десятичный счет распространился на меры массы и объема. Тогда и было создано понятие о десятичной дроби, сохранившей, однако метрологическую форму.В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Уже Лю Хуэй (III век), комментируя извлечение корней в « Математике в девяти книгах», рекомендовал пользоваться дробями со знаменателями 10, 100 и т.д.
Китай
Лю Хуэй


Узбекистан
ал-Каши
В XV веке, в Узбекистане, вблизи города Самарканда, который был тогда богатым культурным центром, жил математик и астроном, основатель астрономической обсерватории, ал-Каши. В 1427 году Ал-Каши написал книгу «Ключ к арифметике», в которой сформулировал основные правила действий с десятичными дробями, способы перевода шестидесятеричных дробей в десятичные и обратно. Целью ал-Каши было дать систему дробей, в которой все операции проводятся так же просто как с целыми числами, но которая основана на общеупотребительном десятичном основании. Десятичная дробь записывалась в одной строке с целой частью числа; для ее обозначения ал-Каши отделял дробь от целого вертикальной чертой или писал другим цветом или надписывал над цифрами названия разрядов, чаще всего называя только низший разряд, определяющий все остальные.


Франция
Франсуа Виет
В 1579 году десятичные дроби применяются в «Математическом каноне» французского математика Франсуа Виета (1540-1603), опубликованном в Париже. В этом сочинении, представляющем собой собрание тригонометрических таблиц, Виет решительно выступил в пользу употребления, как он выражался, тысячных и тысяч, сотых и сотен, десятых и десятков и т.д. взамен шестидесятеричной системы целых и дробей. При записи десятичных дробей Виет не придерживался какого-либо одного обозначения. Нередко он пишет как числитель, так и знаменатель, иногда отделяет цифры целой части от дробной вертикальной чертой, или же цифры целой части изображает жирным шрифтом, или, наконец, цифры дробной части дает более мелким шрифтом и подчеркивает.


Симон Стевин
Голландия
Широкое распространение десятичных дробей в Европе началось только после выхода в свет книги «Десятая» фламандского математика Симона Стевина (1548-1620). Его и считают изобретателем десятичных дробей. Стевин, уроженец Брюгге, вначале был купцом, затем во время Нидерландской революции инженером в войсках возглавлявшего республику Морица Оранского. «Астрологам , земледельцам, мерильщикам объемов, проверщикам емкостей бочек, стереометрам вообще, монетным мастерам и всему купечеству — Симона Стевина привет», — так обращается к своим читателям изобретатель десятичных дробей в своей книге «Десятая»(1585). Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. В книге он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании «изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов».

Стевин обозначает целые знаком 0, десятые – знаком 1, сотые – знаком 2 и т.д., причем цифры 0,1,2,. . . стоят над значащими цифрами или после них в кружках. Например, 5,13 Стевин обозначал
а 0,3752 обозначал


Иоганн Кеплер
Германия
Современную запись десятичных дробей т.е. отделение целой части запятой, предложил Иоганн Кеплер (1571 — 1630 гг.). В странах где говорят по -английски (Англия, США, Канада и др.), вместо запятой пишут точку.


В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого (1703г.)С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. Развитие техники, промышленности и торговли требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.
Основные виды бесконечных десятичных дробей: периодические и непериодические дроби
Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.
Определение 2
Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.
Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть ,143346732…, 3,1415989032…, 153,0245005…, 2,66666666666…, 69,748768152…. и т.д.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.
Определение 3
Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.
К примеру, для дроби 3,444444…. периодом будет цифра 4, а для 76, 134134134134… – группа 134.
Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3,444444…. правильно будет записать как 3,(4), а 76, 134134134134…– как 76,(134).
В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь ,677777 – это то же самое, что ,6(7) и ,6(77) и т.д. Также допустимы записи вида ,67777(7), ,67(7777) и др.
Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.
То есть для указанной выше дроби основной будем считать запись ,6(7), а, например, в случае с дробью 8,9134343434 будем писать 8,91(34).
Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2, то при переводе в десятичную запись из них получатся бесконечные дроби.
В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45,32. В периодическом виде она будет выглядеть как 45,32(). Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.
Отдельно следует остановиться на периодических дробях с периодом 9, например, 4,89 (9), 31,6(9). Они являются альтернативной записью схожих дробей с периодом , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (). Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.
К примеру, дробь 8,31(9) можно заменить на соответствующую ей дробь 8,32(). Или 4,(9)=5,()=5.
Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.
Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.
Определение 4
К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.
Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9,03003000300003… на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.
Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.
Перевод смешанных чисел в десятичные дроби
Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей в знаменателе дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит?
Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.
Сначала записываем цéлую часть и ставим запятую:
3,
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.
Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
3,2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа содержится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем цéлую часть и ставим запятую:
5,
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:
5,03
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа содержится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:
3,
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа содержится число 1000.
Форма записи

При записи десятичной дроби используют следующую форму: сначала пишут целую часть, затем ставят разделитель целой и дробной доли (запятую), а после уже указывают дробную составляющую. Количество цифр, идущих после запятой, зависит от размерности. Различают десятые доли, их записывают одной цифрой, сотые — двумя, тысячные — тремя и так далее.
Записанные десятичные отношения выглядят так: 6,7; 3,26; 0, 234. Их принято указывать без знаменателя. Например, 7/10 = 0,7; 32/100 = 0,32. Удобнее всего пояснить на реальном примере. Пусть есть дробь 69/10. В знаменателе стоит число десять, имеющее один ноль. Отсчитав справа налево в числителе количество знаков, соответствующих числу нулей, в этом случае один, ставят запятую. В рассматриваемом примере запись будет выглядеть как 6,9. Тут 6 — целая часть, а 9 — дробная.
С отношениями можно выполнять любые действия. Их можно складывать, вычитать, делить и умножать. Десятичные дроби — это один из видов отношений. Они соответствуют выражениям, где знаменатель определяется как 10 в степени n, а n — натуральное число, то есть возникающее при счёте естественным образом.
Переход от десятичных дробей к обычным
Обратное преобразование — от десятичной формы записи к обычной — выполняется намного проще. Здесь нет ограничений и специальных проверок, поэтому перевести десятичную дробь в классическую «двухэтажную» можно всегда.
Алгоритм перевода следующий:
- Зачеркните все нули, стоящие в десятичной дроби слева, а также десятичную точку. Это будет числитель искомой дроби. Главное — не переусердствуйте и не зачеркните внутренние нули, окруженные другими цифрами;
- Подсчитайте, сколько знаков стоит в исходной десятичной дроби после запятой. Возьмите цифру 1 и припишите справа столько нулей, сколько знаков вы насчитали. Это будет знаменатель;
- Собственно, запишите дробь, числитель и знаменатель которой мы только что нашли. По возможности, сократите. Если в исходной дроби присутствовала целая часть, сейчас мы получим неправильную дробь, что очень удобно для дальнейших вычислений.
Зачеркнем нули слева и запятые — получим следующие числа (это будут числители): 8; 3107; 225; 72008.
В первой и во второй дробях после запятой стоит по 3 знака, во второй — 2, а в третьей — целых 4 знака. Получим знаменатели: 1000; 1000; 100; 10000.
Наконец, объединим числители и знаменатели в обычные дроби:
Как видно из примеров, полученную дробь очень часто можно сократить. Еще раз отмечу, что любая десятичная дробь представима в виде обычной. Обратное преобразование можно выполнить не всегда.
- Как представить обычную дробь в виде десятичной
- Сложение и вычитание десятичных дробей
- Локальная теорема Муавра — Лапласа
- Видеоурок по задачам C2: уравнение плоскости через определитель
- ЕГЭ-2014 по математике и открытый банк задач
- Задача C1: тригонометрия и показательная функция — 2 вариант
Сложение вычитание десятичных дробей примеры
Чтобы найти разность или сумму 2-х чисел, следует выполнить такие действия:
- Запишите в столбик числа, чтобы совпадали соответствующие разряды. Десятичные точки являются главным ориентиром. Не смотря на то, что они отдельным разрядом не являются, они должны находится на одной вертикали.
- Складывайте или вычитайте столбиком полученные дроби, подобно сложению и вычитанию обычных чисел. Между разрядами ставится десятичная точка.
Больше никаких действий предпринимать не надо. Как мы видим, складываются десятичные дроби, так же, как и обычные.


Необходимо придерживаться следующих правил:
Уравнивать после запятой количество знаков нулями.
Ставить запятые друг под другом.
При сложении или вычитании не обращать внимание на запятую.
Ставить запятую под запятыми
Запятую следует ставить под запятыми, вычитаемых или складываемых дробей.
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя.
Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.
Пример 1. Перевести неправильную дробь в десятичную.
Дробь является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к и хорошенько изучить её.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:
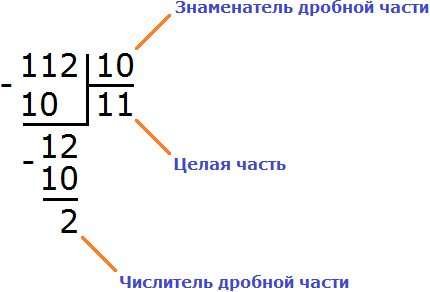
Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:

Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
11,
Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:
11,2
Значит, неправильная дробь при переводе в десятичную обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:
Соберём новое смешанное число — получим . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:
4,
Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
4,50
Значит неправильная дробь при переводе в десятичную обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:
4,50 = 4,5
Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Рациональные числа
Когда у нас было 7 мешков по 6 килограмм, с помощью умножения мы легко посчитали, что общий вес содержимого мешков составляет 42 килограмма. Представим себе, что мы высыпали всё содержимое всех мешков в одну общую кучу массой 42 килограмма. А потом передумали, и захотели распределить содержимое обратно по 7 мешкам. Сколько килограмм при этом попадет в один мешок, если будем распределять поровну? – Очевидно, что 6.
А если захотим распределить 42 килограмма по 6 мешкам? Тут мы подумаем о том, что те же общие 42 килограмма могли бы получиться, если бы мы высыпали в кучу 6 мешков по 7 килограмм. И значит при делении 42 килограмм на 6 мешков поровну получим в одном мешке по 7 килограмм.
А если разделить 42 килограмма поровну по 3 мешкам? И здесь тоже мы начинаем подбирать такое число, которое при умножении на 3 дало бы 42. Для «табличных» значений, как в случае 6 ·7=42 => 42:6=7, мы выполняем операцию деления, просто вспоминая таблицу умножения. Для более сложных случаев используется деление в столбик, которое будет рассмотрено в одной из следующих статей. В случае 3 и 42 можно «подбором» вспомнить, что 3 ·14 = 42. Значит, 42:3=14. В каждом мешке будет по 14 килограмм.
Теперь попробуем разделить 42 килограмма поровну на 5 мешков. 42:5=?
Замечаем, что 5 ·8=40 (мало), а 5·9=45 (много). То есть, ни по 8 килограмм в мешке, ни по 9 килограмм, из 5 мешков мы 42 килограмма никак не получим. При этом понятно, что в реальности разделить любое количество (крупы, например,) на 5 равных частей нам ничего не мешает.
Операция деления целых чисел друг на друга не обязательно дает в результате целое число. Так мы пришли к понятию дроби. 42:5 = 42/5 = 8 целых 2/5 (если считать в обыкновенных дробях) или 42:5=8,4 (если считать в десятичных дробях).
Обыкновенные и десятичные дроби
Обыкновенные дроби хороши тем, что, чтобы представить такой дробью результат деления любых двух целых чисел, нужно просто записать делимое в числитель дроби, а делитель в знаменатель. (123:11=123/11, 67:89=67/89, 127:53=127/53, …) Затем по возможности сократить дробь и/или выделить целую часть (эти действия с обыкновенными дробями будут подробно рассмотрены в следующих статьях). Проблема в том, что производить арифметические действия (сложение, вычитание) с обыкновенными дробями уже не так удобно, как с целыми числами.
Для удобства записи (в одну строку) и для удобства вычислений (с возможностью вычислений в столбик, как для обычных целых чисел) кроме обыкновенных дробей придуманы ещё и десятичные дроби. Десятичная дробь – это специальным образом записанная обыкновенная дробь со знаменателем 10, 100, 1000 и т.п. Например, обыкновенная дробь 7/10 – это то же, что и десятичная дробь 0,7. (8/100 = 0,08; 2 целых 3/10=2,3; 7 целых 1/1000 = 7, 001). Переводу обыкновенных дробей в десятичные и наоборот будет посвящена отдельная статья. Операциям с десятичными дробями – другие статьи.
Любое целое число может быть представлено в виде обыкновенной дроби со знаменателем 1. (5=5/1; −765=−765/1).
Определение: Все числа, которые могут быть представлены в виде обыкновенной дроби, называют рациональными числами. Множество рациональных чисел обозначают буквой Q.
При делении любых двух целых чисел друг на друга (кроме случая деления на 0) всегда получим в результате рациональное число. Для обыкновенных дробей есть правила сложения, вычитания, умножения и деления, позволяющие произвести соответствующую операцию с любыми двумя дробями и получить в результате также рациональное число (дробь или целое).
Множество рациональных чисел – это первое из рассмотренных нами множеств, в котором можно и складывать, и вычитать, и умножать, и делить (кроме деления на 0), никогда не выходя за пределы этого множества (то есть, всегда получая в результате рационально число).
Казалось бы, других чисел не существует, все числа рациональные. Но и это не так.






























