Сравнение десятичных дробей

Действия с десятичными дробями

Десятичные дроби – это обычные числа. Мы можем складывать их, вычитать из одной другую, умножать и делить.

Очень важно уметь правильно производить с ними математические действия, так как зачастую именно от арифметических ошибок зависит твоя оценка на экзамене. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению. Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению

Несомненно, ты знаешь, как все это делать, но на всякий случай, дам тебе краткую инструкцию к применению.

Как складывать десятичные дроби

При сложении десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. Соответственно, запятые стоят четко друг под другом.

Разберемся на примере:

Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставится четко на том же месте, как и в складываемых числах.

Если исходные числа имеют разное количество знаков после запятой, то к дроби с меньшим количеством десятичных знаков нужно приписать необходимое число нулей, чтобы уравнять в дробях количество знаков после запятой.

Если при сложении в сумме мы получаем больше \( 10\), то одна единица прибавляется к сумме при сложении цифр следующего разряда.

Решим наш пример, учтя все правила:

Разобрался? Посчитай в столбик самостоятельно:

• \( 0,0125+0,141\)
• \( 2,4225+0,34\)
• \( 122,4355+1,34\)
• \( 2,435+12,3\)

Сравним ответы:

• \( 0,0125+0,141=0,1535\)
• \( 2,4225+0,34=2,7625\)
• \( 122,4355+1,34=123,7755\)
• \( 2,435+12,3=14,735\)

Общий принцип сравнения десятичных дробей

Исходя из этого принципа сравнения, выводятся правила сравнения десятичных дробей, позволяющие обойтись без перевода сравниваемых десятичных дробей в обыкновенные дроби. Эти правила, а также примеры их применения, мы разберем в следующих пунктах.

По схожему принципу сравниваются конечные десятичные дроби или бесконечные периодические десятичные дроби с натуральными числами , обыкновенными дробями и смешанными числами : сравниваемые числа заменяются соответствующими им обыкновенными дробями, после чего сравниваются обыкновенные дроби.

Что касается сравнения бесконечных непериодических десятичных дробей
, то оно обычно сводится к сравнению конечных десятичных дробей. Для этого рассматривается такое количество знаков сравниваемых бесконечных непериодических десятичных дробей, которое позволяет получить результат сравнения.

Сравнение выражений

Чтобы сравнить две дроби, нужно составить уравнение из их целых частей. Если их части равные, то сравниваются десятые доли. Стоит отметить, что в этом случае учитывают разряд числа. Меньшей будет та дробь, у которой значение числа в разряде меньше.

Для того чтобы провести сравнение дробей, применяют следующую последовательность действий:

• Пробуют сократить выражения.
• Приводят дроби к одинаковому числу знаков путём дописывания в случае необходимости нулей.
• Выполняют сравнение по старшинству разрядов, начиная с целой части, а в случае равенства — с десятой, сотой и так далее.
• Если при сравнении разрядов один из них будет больше или меньше, задача считается выполненной.

Например, нужно сравнить дроби 237,4 и 238,2 и результат выразить через процентное отношение. Так как 237 меньше 238, то дробные части сравнивать уже будет не нужно. Для того чтобы определить процентное отношение, большую часть принимают за 100%, а меньшую — за X. Составляют пропорцию и делают вычисление: 237,4 * 100 = 238,2 * Х.

Это обыкновенное уравнение с одним неизвестным: Х = 237,4 * 100 / 238,2 = 99,66%. То есть первое выражение меньше второго на 100 — 99,66 = 0,34%. Десятичные выражения, как и натуральные, можно записывать в ряд, а значит, откладывать на координатной прямой. На ней правее будет стоять отношение, которое больше.

Небольшие задания решать несложно

Но существуют задачи, для решения которых нужно не только проявить максимальное внимание, но и затратить много времени. Например, как при вычислении совместных дробей

В таких случаях есть резон использовать калькулятор десятичных дробей с запятыми онлайн. Чтобы им воспользоваться, особых знаний не нужно. Загрузив сайт и введя в таблицу исходные данные, пользователю нужно всего лишь нажать кнопку «Рассчитать» и получить точный результат.

Как сравнивать десятичные дроби: первый способ

Если мы сравниваем дроби с разным количеством знаком после запятой, нужно сделать количество десятичных знаков одинаковым.

Рисунок 2

Длина сирийского хомяка Тоши $12.752$ см, а длина его брата Тиши $12.76$ см. Чтобы правильно сравнить их размеры, сначала уравняем количество десятичных знаков, для этого к размеру Тиши припишем $0$, вот так: $12.760$.

Если теперь записать размеры хомячков в виде неправильных дробей, получится так:

$12.752=\frac{12752}{1000}$

$12.760=\frac{12760}{1000}$

У нас две дроби с одинаковыми знаменателями. Значит, больше будет та, у которой больше числитель.

$\frac{12752}{1000}<\frac{12760}{1000}$

Сравнивать десятичные дроби можно двумя способами.

{"questions":,"x":1}}},{"content":"$0.1$ `fill_choice-18` $0.09$<br />$0.07$ `fill_choice-30` $0.09$<br />$0.015$ `fill_choice-52` $0.02$","widgets":{"fill_choice-18":{"type":"fill_choice","options":,"answer":1},"fill_choice-30":{"type":"fill_choice","options":,"answer":0},"fill_choice-52":{"type":"fill_choice","options":,"answer":0}}},{"content":"Расположите числа по убыванию`sorter-82`","widgets":{"sorter-82":{"type":"sorter","items":,"x":1}}}]}

Перевод обыкновенных дробей в десятичные дроби

Обозначим последовательность, в которой мы будем разбираться с переводом обыкновенных дробей в десятичные дроби.

После этого мы пойдем дальше и покажем, как любую обыкновенную дробь (не только со знаменателями 10, 100, … ) записать в виде десятичной дроби. При таком обращении обыкновенных дробей получаются как конечные десятичные дроби, так и бесконечные периодические десятичные дроби.

Теперь обо всем по порядку.

Перевод обыкновенных дробей со знаменателями 10, 100, … в десятичные дроби

Некоторые правильные обыкновенные дроби перед переводом в десятичные дроби нуждаются в «предварительной подготовке». Это касается обыкновенных дробей, количество цифр в числителе которых меньше, чем количество нулей в знаменателе. Например, обыкновенную дробь 2/100 нужно предварительно подготовить к переводу в десятичную дробь, а дробь 9/10 в подготовке не нуждается.

«Предварительная подготовка» правильных обыкновенных дробей к переводу в десятичные дроби заключается в дописывании слева в числителе такого количества нулей, чтобы там общее количество цифр стало равно количеству нулей в знаменателе. Например, дробь

После подготовки правильной обыкновенной дроби можно приступать к ее обращению в десятичную дробь.

Рассмотрим применение этого правила при решении примеров.

Переведите правильную обыкновенную дробь 37/100 в десятичную.

Для закрепления навыков перевода правильных обыкновенных дробей с числителями 10, 100, … в десятичные дроби разберем решение еще одного примера.

Запишите правильную дробь 107/10 000 000 в виде десятичной дроби.

Разберем применение этого правила при решении примера.

Переведите неправильную обыкновенную дробь 56 888 038 009/100 000 в десятичную дробь.

Рассмотрим пример, при решении которого выполним все необходимые шаги для представления смешанного числа в виде десятичной дроби.

Переведите смешанное число

Запишем все решение кратко:

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В остальных случаях приходится использовать другой способ перевода обыкновенной дроби в десятичную, к рассмотрению которого мы и переходим.

Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель, числитель предварительно заменяется равной ему десятичной дробью с любым количеством нулей после десятичной запятой (об этом мы говорили в разделе равные и неравные десятичные дроби). При этом деление выполняется так же, как деление столбиком натуральных чисел, а в частном ставится десятичная запятая, когда заканчивается деление целой части делимого. Все это станет понятно из решений примеров, приведенных ниже примеров.

Переведите обыкновенную дробь 621/4 в десятичную дробь.

Так мы добрались до десятичной запятой в делимом, а остаток при этом отличен от нуля. В этом случае в частном ставим десятичную запятую, и продолжаем деление столбиком, не обращая внимания на запятые:

Для закрепления материала рассмотрим решение еще одного примера.

Переведите обыкновенную дробь 21/800 в десятичную дробь.

Запишите обыкновенную дробь 19/44 в виде десятичной дроби.

Для перевода обыкновенной дроби в десятичную выполним деление столбиком:

В заключение этого пункта разберемся, какие обыкновенные дроби можно перевести в конечные десятичные дроби, а какие – только в периодические.

Пусть перед нами находится несократимая обыкновенная дробь (если дробь сократимая, то предварительно выполняем сокращение дроби), и нам нужно выяснить, в какую десятичную дробь ее можно перевести – в конечную или периодическую.

Обыкновенные дроби не переводятся в бесконечные непериодические десятичные дроби

Информация предыдущего пункта порождает вопрос: «Может ли при делении числителя дроби на знаменатель получиться бесконечная непериодическая дробь»?

Ответ: нет. При переводе обыкновенной дроби может получиться либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Поясним, почему это так.

Других вариантов быть не может, следовательно, при обращении обыкновенной дроби в десятичную дробь не может получиться бесконечная непериодическая десятичная дробь.

Из приведенных в этом пункте рассуждений также следует, что длина периода десятичной дроби всегда меньше, чем значение знаменателя соответствующей обыкновенной дроби.

Равные и неравные десятичные дроби

Сначала введем определения равных и неравных конечных десятичных дробей.

Определение.

Две конечные десятичные дроби называются равными, если равны соответствующие им обыкновенные дроби, в противном случае эти десятичные дроби называются неравными.

На основании этого определения легко обосновать следующее утверждение: если в конце данной десятичной дроби приписать или отбросить несколько цифр , то получится равная ей десятичная дробь. Например, 0,3=0,30=0,300=…, а 140,000=140,00=140,0=140.

Действительно, дописывание или отбрасывание в конце десятичной дроби нуля справа соответствует умножению или делению на 10 числителя и знаменателя соответствующей обыкновенной дроби. А мы знаем основное свойство дроби, которое гласит, что умножение или деление числителя и знаменателя дроби на одно и то же натуральное число дает дробь, равную исходной. Этим доказано, что дописывание или отбрасывание нулей справа в дробной части десятичной дроби дает дробь, равную исходной.

Например, десятичной дроби 0,5 отвечает обыкновенная дробь 5/10, после дописывания нуля справа получается десятичная дробь 0,50, которой отвечает обыкновенная дробь 50/100, а . Таким образом, 0,5=0,50. Обратно, если в десятичной дроби 0,50 отбросить справа , то мы получим дробь 0,5, так от обыкновенной дроби 50/100 мы придем к дроби 5/10, но . Следовательно, 0,50=0,5.

Переходим к определению равных и неравных бесконечных периодических десятичных дробей.

Определение.

Две бесконечные периодические дроби равны, если равны отвечающие им обыкновенные дроби; если же соответствующие им обыкновенные дроби не равны, то сравниваемые периодические дроби тоже не равны.

Из данного определения следуют три вывода:

• Если записи периодических десятичных дробей полностью совпадают, то такие бесконечные периодические десятичные дроби равны. Например, периодические десятичные дроби 0,34(2987) и 0,34(2987) равны.
• Если периоды сравниваемых десятичных периодических дробей начинаются с одинаковой позиции, первая дробь имеет период , вторая – период 9, и значение разряда, предшествующего периоду на единицу больше, чем значение разряда, предшествующего периоду 9, то такие бесконечные периодические десятичные дроби равны. Например, периодические дроби 8,3(0) и 8,2(9) равны, также равны дроби 141,(0) и 140,(9).
• Две любые другие периодические дроби не являются равными. Приведем примеры неравных бесконечных периодических десятичных дробей: 9,0(4) и 7,(21), 0,(12) и 0,(121), 10,(0) и 9,8(9).

Осталось разобраться с равными и неравными бесконечными непериодическими десятичными дробями. Как известно, такие десятичные дроби не могут быть переведены в обыкновенные дроби (такие десятичные дроби представляют иррациональные числа), поэтому сравнение бесконечных непериодических десятичных дробей нельзя свести к сравнению обыкновенных дробей.

Определение.

Две бесконечные непериодические десятичные дроби равны, если их записи полностью совпадают.

Но есть один нюанс: невозможно увидеть «законченную» запись бесконечных непериодических десятичных дробей, следовательно, невозможно убедиться и в полном совпадении их записей. Как же быть?

При сравнении бесконечных непериодических десятичных дробей рассматривают лишь конечное число знаков сравниваемых дробей, которое позволяет сделать необходимые выводы. Таким образом, сравнение бесконечных непериодических десятичных дробей сводится к сравнению конечных десятичных дробей.

При таком подходе можно говорить о равенстве бесконечных непериодических десятичных дробей лишь с точностью до рассматриваемого разряда. Приведем примеры. Бесконечные непериодические десятичные дроби 5,45839… и 5,45839… равны с точностью до стотысячных, так как равны конечные десятичные дроби 5,45839 и 5,45839; непериодические десятичные дроби 19,54… и 19,54810375… равны с точностью до сотых, так как равны дроби 19,54 и 19,54.

Неравенство бесконечных непериодических десятичных дробей при таком подходе устанавливается вполне определенно. Например, бесконечные непериодические десятичные дроби 5,6789… и 5,67732… не равны, так как очевидны различия в их записях (не равны конечные десятичные дроби 5,6789 и 5,6773). Бесконечные десятичные дроби 6,49354… и 7,53789… тоже не равны.

Перевод десятичных чисел в обыкновенную дробь

Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.

Представление дробей

Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:

• 0,5 = 1/2;
• 0,25 = 1/4;
• 1,375 = 11/8.

И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.

Избавляемся от запятой

Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:

Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.

Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:

• 0,5/1 = 5/10;
• 0,25/1 = 2,5/10 = 25/100;
• 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.

Шаг 3: Сокращаем полученные дроби до удобоваримого вида:

• 5/10 = 1 × 5 / 2 × 5 = 1/2;
• 25/100 = 1 × 25 / 4 × 25 = 1/4;
• 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.

Избавляемся от запятой еще проще

Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.

Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.

Шаг 2: Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:

• для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
• для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.

По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.

Шаг 3: Сокращаем нули и получаем итоговый результат:

• 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
• 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.

Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.

Преобразование на слух

Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.

0,025 = 25/1000 = 1/40

Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.

Примеры использования дробей в повседневной жизни

На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.

Работа

Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.

К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:

0,12 = 12/100 = 3/25

Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.

Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.

Слайды и текст этой презентации

Слайд 1

Текст слайда:

История возникновения десятичных дробей

Слайд 2

Текст слайда:

Зарождение десятичных дробей произошло в Китае Уже во II веке до н.э. там существовала десятичная система мер длины. Примерно в III веке н.э. десятичный счет распространился на меры массы и объема. Тогда и было создано понятие о десятичной дроби, сохранившей, однако метрологическую форму.В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Уже Лю Хуэй (III век), комментируя извлечение корней в « Математике в девяти книгах», рекомендовал пользоваться дробями со знаменателями 10, 100 и т.д.

Китай
Лю Хуэй

Слайд 3

Слайд 4

Текст слайда:

Узбекистан
ал-Каши

В XV веке, в Узбекистане, вблизи города Самарканда, который был тогда богатым культурным центром, жил математик и астроном, основатель астрономической обсерватории, ал-Каши. В 1427 году Ал-Каши написал книгу «Ключ к арифметике», в которой сформулировал основные правила действий с десятичными дробями, способы перевода шестидесятеричных дробей в десятичные и обратно. Целью ал-Каши было дать систему дробей, в которой все операции проводятся так же просто как с целыми числами, но которая основана на общеупотребительном десятичном основании. Десятичная дробь записывалась в одной строке с целой частью числа; для ее обозначения ал-Каши отделял дробь от целого вертикальной чертой или писал другим цветом или надписывал над цифрами названия разрядов, чаще всего называя только низший разряд, определяющий все остальные.

Слайд 5

Слайд 6

Текст слайда:

Франция
Франсуа Виет

 В 1579 году десятичные дроби применяются в «Математическом каноне» французского математика Франсуа Виета (1540-1603), опубликованном в Париже. В этом сочинении, представляющем собой собрание тригонометрических таблиц, Виет решительно выступил в пользу употребления, как он выражался, тысячных и тысяч, сотых и сотен, десятых и десятков и т.д. взамен шестидесятеричной системы целых и дробей. При записи десятичных дробей Виет не придерживался какого-либо одного обозначения. Нередко он пишет как числитель, так и знаменатель, иногда отделяет цифры целой части от дробной вертикальной чертой, или же цифры целой части изображает жирным шрифтом, или, наконец, цифры дробной части дает более мелким шрифтом и подчеркивает.

Слайд 7

Слайд 8

Текст слайда:

Симон Стевин
Голландия

Широкое распространение десятичных дробей в Европе началось только после выхода в свет книги «Десятая» фламандского математика Симона Стевина (1548-1620). Его и считают изобретателем десятичных дробей. Стевин, уроженец Брюгге, вначале был купцом, затем во время Нидерландской революции инженером в войсках возглавлявшего республику Морица Оранского. «Астрологам , земледельцам, мерильщикам объемов, проверщикам емкостей бочек, стереометрам вообще, монетным мастерам и всему купечеству — Симона Стевина привет», — так обращается к своим читателям изобретатель десятичных дробей в своей книге «Десятая»(1585). Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. В книге он старается убедить людей пользоваться десятичными дробями, говоря, что при их использовании «изживаются трудности, распри, ошибки, потери и прочие случайности, обычные спутники расчетов».

Слайд 9

Текст слайда:

Стевин обозначает целые знаком 0, десятые – знаком 1, сотые – знаком 2 и т.д., причем цифры 0,1,2,. . . стоят над значащими цифрами или после них в кружках. Например, 5,13 Стевин обозначал

а 0,3752 обозначал

Слайд 10

Слайд 11

Текст слайда:

Иоганн Кеплер
Германия

Современную запись десятичных дробей т.е. отделение целой части запятой, предложил Иоганн Кеплер (1571 — 1630 гг.). В странах где говорят по -английски (Англия, США, Канада и др.), вместо запятой пишут точку.

Слайд 12

Слайд 13

Текст слайда:

В России первые систематические сведения о десятичных дробях встречаются в “Арифметике” Магницкого (1703г.)С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. Развитие техники, промышленности и торговли требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.

Можно ли любую обыкновенную дробь перевести в десятичную

Ответ на этот вопрос — «Да». Любую обыкновенную дробь можно записать в виде конечной или бесконечной десятичной, периодической дроби. У каждой дроби всегда есть эквивалентное представление в десятичной форме.

Теперь, прежде чем вы приступите к преобразованию обыкновенной дроби в десятичную, обратите внимание на следующие полезные советы:

1. Используйте калькулятор: Если у вас есть доступ к калькулятору, лучше воспользуйтесь им для выполнения деления. Это упростит и ускорит процесс.
2. Округление: При округлении десятичной дроби рекомендуется использовать «четное округление», то есть округлять до ближайшего четного числа.
3. Проверьте результат: После окончания преобразования проверьте результат с помощью других методов или калькулятора, чтобы убедиться в его точности.

Выводы:

Перевод обыкновенной дроби в десятичную форму может быть выполнен различными способами, включая деление числителя на знаменатель и умножение на определенное число

Независимо от выбранного подхода, важно следовать указанным шагам и быть внимательным при округлении результатов. При необходимости всегда лучше проверять результаты с помощью других методов или с использованием калькулятора, чтобы быть уверенным в их точности

Можно ли бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби

Для доказательства этого факта необходимо воспользоваться алгебраическими операциями и свойствами рациональных чисел. Первым шагом можно представить бесконечную десятичную периодическую дробь в виде обыкновенной бесконечной десятичной периодической дроби, умножив исходную дробь на 10. Затем, в результате вычислений, можно выделить две части этой периодической дроби — целую и периодическую.

Затем, используя формулы и свойства обыкновенных дробей, можно свести данную бесконечную периодическую дробь к виду обыкновенной. Если период равен нулю, то получится обыкновенная дробь без остатка, а если период не равен нулю, то бесконечную периодическую дробь можно записать в виде обыкновенной, где числитель выражен через разность между периодом и целой частью, а знаменатель равен разности между числителем и целой частью.

Таким образом, любую бесконечную десятичную периодическую дробь можно записать в виде обыкновенной дроби, что означает, что она является рациональным числом.

Как десятичную дробь прибавить к обычной дроби

Для сложения десятичных дробей необходимо следовать нескольким шагам. В начале, нужно записать оба числа одно под другим так, чтобы запятая стояла под запятой в обоих числах. Затем производится сложение чисел, при этом сложение осуществляется как обычное сложение чисел в столбик, начиная с самого правого разряда. После сложения всех разрядов, запятая в итоговом ответе будет расположена под запятой. Если в процессе сложения получилось число, у которого количество разрядов после запятой больше, чем десятичная дробь, пишется результат с штрихом на запятой и продолжается сложение следующих разрядов. Итоговая сумма будет содержать десятичную дробь, если она присутствовала в исходных числах.

Как преобразовать десятичную дробь в обыкновенную примеры

Далее мы должны упростить полученную обыкновенную дробь. Для этого умножим числитель и знаменатель на 10, пока в числителе не станет только цифры после запятой. Например, в случае с дробью 0,35 мы умножаем числитель и знаменатель на 10, получаем 3,5/10. При этом, если в какой-то момент мы получаем дробь без нулей после запятой, мы умножаем числитель и знаменатель на 1000, 10000 и так далее, чтобы убрать все цифры после запятой в числителе.

После упрощения дроби, мы можем сократить ее, если это возможно. Для этого находим наибольший общий делитель числителя и знаменателя и делим оба на него. В итоге получается обыкновенная дробь в виде a/b, где a и b — целые числа.

Как разделить обыкновенную дробь на целое число

Для того чтобы разделить обыкновенную дробь на целое число, нужно умножить знаменатель дроби на данное целое число, а числитель оставить без изменений. Например, если у нас есть дробь 3/4 и мы хотим разделить ее на число 2, мы умножаем знаменатель 4 на 2 и получаем 8. Числитель остается без изменений и равен 3. Таким образом, исходная дробь 3/4 разделяется на 2, и мы получаем дробь 3/8. Это означает, что одна часть дроби 3/4 равна 3/8. Таким образом, мы можем разделить обыкновенную дробь на целое число, умножив знаменатель на это число и оставив числитель без изменений.

Понятие десятичной дроби

Прежде чем мы расскажем вам, как сравнивать десятичные дроби, давайте рассмотрим основные определения, виды дробей и разницу между ними.

Дробь — это число в математике, где a и b — числа или выражения. На самом деле это только одна из форм, в которой может быть представлено число.Существует два формата записи:

• обычный дисплей — 1/2 или a/b,
• десятичная форма — 0,5.

В правильной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда стоит делитель, который называется знаменателем. Линия между числителем и знаменателем означает деление.

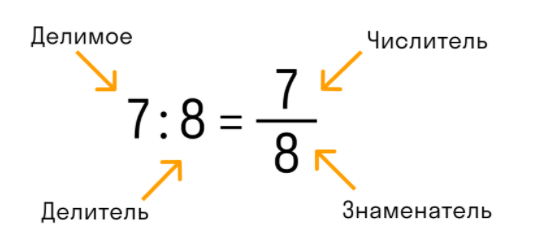
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т д. По сути, десятичная дробь — это то, что получается при делении числителя на знаменатель. Оно пишется в строке через запятую, чтобы отделить целую часть от дробной. Как это:

• 0,1
• 2,53
• 9932

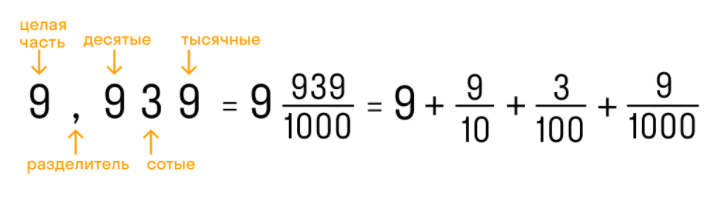
Конечный десятичный знак — это когда количество цифр после запятой точно определено.

Бесконечное десятичное число — это когда количество цифр после запятой бесконечно. Для удобства математики договорились округлить эти числа до 1-3 после запятой.

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить
или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac{30}{45}\).

Решение:
Решим двумя способами:Первый способ:

Распишем дробную часть на простые множители, а целую часть не будем трогать.

\(2\frac{30}{45}=2\frac{2 \times \color{red} {5 \times 3}}{3 \times \color{red} {5 \times 3}}=2\frac{2}{3}\)

Второй способ:

Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

\(2\frac{30}{45}=\frac{45 \times 2 + 30}{45}=\frac{120}{45}=\frac{2 \times \color{red} {5 \times 3} \times 2 \times 2}{3 \times \color{red} {3 \times 5}}=\frac{2 \times 2 \times 2}{3}=\frac{8}{3}=2\frac{2}{3}\)

Вопросы по теме:

Можно ли сокращать дроби при сложении или вычитании?


Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Вычислите выражение \(\frac{50+20-10}{20}\) .

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

\(\frac{50+\color{red} {20}-10}{\color{red} {20}}=\frac{60}{20}=\frac{3 \times 20}{20}=\frac{3}{1}=3\)

На какие числа можно сокращать дробь?


Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac{100}{150}\).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

\(\frac{100}{150}=\frac{2 \times 50}{3 \times 50}=\frac{2}{3}\)

Получили несократимую дробь \(\frac{2}{3}\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac{100}{150}\) на 2.

\(\frac{100}{150}=\frac{2 \times 50}{2 \times 75}=\frac{50}{75}\)

Получили сократимую дробь \(\frac{50}{75}\).

Какие дроби можно сокращать?


Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac{4}{8}\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:

Сравните две дроби \(\frac{2}{3}\) и \(\frac{8}{12}\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac{8}{12}\):

\(\frac{8}{12}=\frac{2 \times 4}{3 \times 4}=\frac{2}{3} \times \frac{4}{4}=\frac{2}{3} \times 1=\frac{2}{3}\)

Отсюда получаем, \(\frac{8}{12}=\frac{2}{3}\)

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:

Сократите если возможно следующие дроби: а) \(\frac{90}{65}\) б) \(\frac{27}{63}\) в) \(\frac{17}{100}\) г) \(\frac{100}{250}\)

Решение:
а) \(\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}\)
б) \(\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}\)
в) \(\frac{17}{100}\) несократимая дробь
г) \(\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}\)