Вычитание дробей

Дроби — коротко о главном

Определения:

Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.

Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.

Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.

Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle  \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).

Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),

\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).

Основное свойство дроби: 

Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).

Действия с дробями:

Сложение/вычитание дробей

• две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
• две обыкновенные дроби с разными знаменателями:
  • приводим дроби к наименьшему общему знаменателю;
  • складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
  • сокращаем полученную дробь
• две смешанные дроби с разными знаменателями:
  • приводим дробные части этих чисел к наименьшему общему знаменателю;
  • по-отдельности складываем/вычитаем целые части и дробные части;
  • если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
  • сокращаем полученную дробь.

Умножение дробей

• умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
• умножение двух обыкновенных дробей:
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь
• умножение двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • перемножаем числители и знаменатели дробей;
  • сокращаем полученную дробь;
  • если получилась неправильная дробь преобразовываем ее в смешанную.

Деление дробей

• деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
• деление натурального числа на дробь: число умножаем на дробь обратную данной
• деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
• деление двух смешанных чисел:
  • преобразовываем смешанные дроби в неправильные;
  • умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.

Сокращение дроби

Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).

Приведение дробей к наименьшему общему знаменателю

• найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
• разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
• умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.

Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).

Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).

Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).

Преобразования неправильной дроби в смешанную дробь

• поделите числитель дроби на ее знаменатель;
• остаток от деления запишите в числитель, знаменатель оставьте прежним;
• результат от деления запишите в качестве целой части.

Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).

Сравнение дробей:

• две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
• две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
• две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше

Действия над смешанными числами

Смешанное число — математическое выражение, в состав которого входят целая величина и обыкновенная правильная дробь. Например, 7[1/3] является смешанным, целая часть — 7 и дробная — 1/3. Последняя заключается в квадратные скобки. В смешанное выражение могут конвертироваться только целые числа и неправильные дроби.

Для каждого вида конвертации существует определенная методика. Специалисты предлагают только 2 алгоритма преобразования:

1. Целого числа.
2. Неправильной дроби.

В первом случае операция выполняется довольно просто. Однако начинающим математикам рекомендуется пока придерживаться методики. Неправильную дробь необходимо конвертировать по усложненному алгоритму при помощи специальной формулы. Последняя формирует новый числитель.

Представление целой величины

Необязательно исходным значением может быть неправильная дробь. Каждое целое число можно представить в виде смешанного при помощи такого алгоритма:

1. Записать величину.
2. Отнять от целой части единицу.
3. Указать в скобках дробь — единичное значение.
4. Написать результат.

Реализация методики выполняется на примере числа 7, которое нужно представить в смешанной форме. Операция выглядит таким образом:

1. Записать число: 7.
2. Величина без учета единицы: 6.
3. Дробь: 2/2.
4. Полная запись: 6[2/2].

Конвертация неправильного дробного тождества

В случае конвертации числа, представленного в виде обыкновенной дроби, необходимо воспользоваться определенным алгоритмом. Он выглядит таким образом:

1. Записать число смешанного типа.
2. Выделить целую часть.
3. Рассчитать «новый» числитель по формуле: Q’=Q-C*Z, где Q — искомая величина числителя, C — целое число и Z — знаменатель.
4. Результат: Q’/Z.

Реализацию алгоритма нужно разобрать на примере «78/7» для закрепления теоретических знаний. Решать его нужно следующим образом:

1. Записать значение: 78/7.
2. Выделить целое значение (часть): 78/7=11.
3. Найти величину нового числителя: 78−11*7=1, где 78 — числитель искомой неправильной дроби, 7 — ее знаменатель и 11 — целая часть.
4. Написать результат: 11[1/7].

Специалисты рекомендуют на начальных этапах обучения четко следовать методике. Со временем надобность в ней исчезнет, поскольку операция преобразования будет выполняться на автоматизме. Далее необходимо разобрать алгоритм обратной конвертации.

Обратная операция

Для проверки правильности конвертации неправильной дроби в смешанное число или решения задач необходимо воспользоваться специальным алгоритмом. Он имеет следующий вид:

1. Записать смешанное тождество.
2. Вычислить величину нового числителя: Q=Q’+C*Z, где Q’ — исходная величина числителя, C — целое значение и Z — знаменатель.
3. Записать результат: Q/Z.

Чтобы понять принцип работы алгоритма, необходимо разобрать пример 11[1/7]. Он должен решаться таким способом:

1. Написать смешанное тождество: 11[1/7].
2. Числитель: 11*7+1=78.
3. Искомый результат: 78/7.

При помощи этого алгоритма можно осуществлять операцию преобразования в целое число.

Таким образом, смешанное число — вид дробного выражения, которое применяется при решении задач. Для его конвертации необходимо знать соответствующие методики.

Сложение дробей с одинаковыми знаменателями

{"questions":[{"content":"Мама готовила бутерброды. Она разрезала батон на $11$ частей. Каждый кусочек равен $\\frac{1}{11}$ батона. Для бутербродов она взяла $4$ кусочка колбасы и $5$ ломтиков сыра. Получилось $9$ бутербродов.`image-1`Сколько частей батона было задействовано на приготовление всех бутербродов?`fill_choice_big-6`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/09/slozhenie-drobej.svg"},"fill_choice_big-6":{"type":"fill_choice_big","options":,"placeholder":0,"answer":0}}}]}

$$\frac{\textcolor{blue}{4}}{\textcolor{coral}{11}}+\frac{\textcolor{blue}{5}}{\textcolor{coral}{11}}=\frac{\textcolor{blue}{4}+\textcolor{blue}{5}}{\textcolor{coral}{11}}=\frac{\textcolor{blue}{9}}{\textcolor{coral}{11}}$$

Практика

Закрепите новый навык на нашем тренажере сложения дробей.

{"questions":[{"content":"Из помидоров массой $\\frac{4}{15}$ $кг$ и огурцов массой $\\frac{7}{15}$ $кг$ сделали салат.`image-1` Какова масса салата?`choice-15`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/07/salat-stoleshnitsa-zelen.svg","width":"400"},"choice-15":{"type":"choice","options":,"answer":}},"step":1,"hints":}]}

Алгоритм вычитания

Прибавление (вычитание) дробей от целых и дробных чисел — одна из основных математических операций в алгебре. Следует отметить, что вычитаемые числа могут быть как с одинаковым знаменателем, так и разным. Поэтому используются два принципиально отличающихся способа. Для успешного вычитания смешанных дробей эти правила нужно обязательно знать и уметь применять на практике.

При одинаковых делимых правило вычитания довольно простое. В ответе знаменатель остаётся неизменным, а в числитель записывается разность уменьшаемого делителя с вычитаемым. Например, 13/19 — 5/19 = (13 — 5)/19 = 8/19. Если знаменатели отличаются, то необходимо найти наименьший знаменатель, которым является наименьшее общее кратное. Определить его можно несколькими способами.

Самый простой — перемножить делители между собой. Но этот способ неоптимальный и может привести к усложнению действий. Поэтому каждый знаменатель раскладывают на множители. В разложении совпадающие цифры убирают, а оставшиеся перемножают. В ответе и будет наименьший общий знаменатель (НОЗ). Как только НОЗ найден, вычисляют дополнительные множители. Делают это делением найденного числа на знаменатель каждой дроби. Полученные результаты умножают на числители, которые после вычитают.

Эти два важных правила используются и в алгоритме вычитания смешанных дробей. Объяснение его можно представить в виде последовательности следующих действий:

1. Из целой части первого числа вычитают целую часть второго.
2. Находят разницу дробных записей.
3. Записывают ответ, состоящий из целой и дробной части по правилу смешанного числа.

Этот алгоритм справедлив для любого выражения, дробная составляющая членов которого имеет одинаковый знаменатель. Если же он разный, то сначала необходимо найти НОЗ.

В этом случае используют метод занимания единицы. В его сути лежит возможность уменьшения целой части на единицу с последующим увеличением числителя на значение знаменателя. Например, 10 9/15 = 9 (9+15)/15 = 9 24/15. Если же вычитать нужно из натурального числа смешанное, то первое раскладывают так, чтобы получилась дробь. Например, смешанное число 6 при вычитании можно представить как 5 + 1 или 5 + 16/16. Значение дробной части подбирается таким образом, чтобы знаменатель образованной дроби совпадал с делителем вычитаемого числа.

Правила деления дробей

Деление дробей – это достаточно непростая процедура, которая требует понимания определенных особенностей и механик действий. Для того, чтобы получить результат, необходимо перемножить противоположные числители и знаменатели. Чтобы лучше понимать механику процедуры, рекомендуется рассмотреть следующий пример:

Как видно, если понимать особенности проведения математической операции, а также учитывать определенные особенности в каждом случае, то выполнение данной процедуры возможно всего в несколько кликов

Следует обратить внимание на такие базовые правила деления дробей:

• Если планируется делить обычные дроби, тогда необходимо просто перемножить противоположные числители и знаменатели. В результате получается дробь, которую можно сократить при необходимости.
• Если необходимо поделить дробь на натуральное число, то необходимо умножить знаменатель на число, но при этом числитель остается без каких-либо изменений.
• Если натуральное число делят на дробь, действует немного другое правило. Необходимо умножать число на обратную дробь. Это означает, что числитель и знаменатель дроби нужно поменять местами.
• При делении двух обычных дробей нужно перемножить дроби. При этом во второй дроби необходимо числитель и знаменатель поменять местами для того, чтобы получить искомый результат.

Если проводится процедура деления смешанных дробей, правила немного отличаются, что следует учитывать. Сейчас не требуется обязательно знать все правила наизусть, но понимать базовые принципы проведения описанных операций рекомендуется, чтобы достичь поставленных задач намного быстрее и избежать возможных ошибок. С помощью специального онлайн-калькулятора, вы можете разделить дробь онлайн всего в несколько кликов, получив максимально точное число, которое можно использовать для выполнения прочих математических операций.

Что делать, если у дроби есть целая часть

Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.

Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:

1. Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
2. Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
3. Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.

Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:

Задача. Найдите значение выражения:

Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:

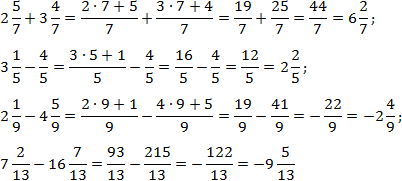
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.

Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.

Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.

Действия между обыкновенными и десятичными дробями

Теперь давайте посмотрим, как складывать и вычитать обычные дроби и десятичные дроби.

Здесь к началу алгоритма добавлен еще один этап: преобразование десятичной дроби в обыкновенную.

Делается это довольно легко. Посмотрим, как именно.

Во-первых, вам нужно переписать исходную дробь в новую дробь, где будет одна десятичная дробь в числителе и одна в знаменателе:

( mathbf {0.01 = frac {0.01} {1}} ) ( mathbf {0.3 = frac {0.3} {1}})

А затем мы просто умножаем числитель и знаменатель дроби на 10, пока числитель не станет больше или равным единице:

( mathbf { frac {0.01} {1} = frac {0.01 cdot10} {1 cdot10} = frac {0.1} {10} = frac {0.1 cdot10} {10 cdot10} = гидроразрыв {1} {100}})

( mathbf { frac {0.3} {1} = frac {0.3 cdot10} {1 cdot10} = frac {3} {10}})

Как видите, все довольно просто.

Кроме того, вы можете подсчитать суммы и разницы с полученными обычными дробями так же, как мы это делали раньше.

Посмотрим на несколько примеров.

Вычислите разницу ( mathbf { frac {1} {3} -0.1}):

Для начала нужно преобразовать десятичную дробь в обыкновенную:

( mathbf {0.1 = frac {0.1} {1} = frac {0.1 cdot10} {1 cdot10} = frac {1} {10}})

Теперь нам нужно привести дроби к общему знаменателю

( mathbf { frac {1} {3} — frac {1} {10} = frac {1 cdot10} {3 cdot10} — frac {1 cdot3} {10 cdot3} = frac {10} {30} — frac {3} {30} = frac {10-3} {30} = frac {7} {30}})

Проверяем, что дробь нельзя стереть, и приходим к выводу, что это ответ.

Вычислить сумму ( mathbf {0.4+ frac {1} {4}})

Снова преобразуем десятичную дробь в обыкновенную:

( mathbf {0.4 = frac {0.4} {1} = frac {0.4 cdot10} {1 cdot10} = frac {4} {10}})

Мы не уменьшаем дробь намеренно, поэтому, если нам нужно дополнительно умножить на 2, нам не нужно предпринимать ненужных действий.

Далее сводим дроби к общему знаменателю и вычисляем сумму:

( mathbf { frac {4} {10} + frac {1} {4} = frac {4 cdot2} {10 cdot2} + frac {1 cdot5} {4 cdot5} = frac {8} {20} + frac {5} {20} = frac {8 + 5} {20} = frac {13} {20}})

Это то количество, которое нам нужно.

Как делить обыкновенные и десятичные дроби

Деление одной дроби на другую — это умножение её на вторую дробь в перевёрнутом виде

В отличие от сложения и вычитания, при делении неважно, какие у дробей знаменатели: одинаковые или разные. Просто умножьте числитель на числитель, а знаменатель на знаменатель и, если у вас получится неправильная дробь, выделите из неё целую часть

Например, вам нужно разделить 3 /₅ на 4 /₉. Для этого поменяйте местами числитель и знаменатель второй дроби — она превратится в 9 /₄ — и умножьте 3 /₅ на неё.

Если в примере изначально есть смешанные числа, как 1 7 /₂₀, сначала нужно перевести их в неправильные дроби (в данном случае получится 27 /₂₀), а потом делить, как описано выше.

На целое число

Чтобы разделить обыкновенную дробь на целое число, нужно представить его также в виде обыкновенной дроби: в числителе будет оно само, а в знаменателе единица. А затем делить как дробь на дробь. Например:

Можно действовать и ещё проще: умножить знаменатель на данное в примере число, а числитель оставить как есть.

А чтобы, наоборот, разделить целое число на обыкновенную дробь, нужно перевернуть эту дробь и умножить число на неё. Например:

Как делить десятичные дроби

На другую дробь

Это можно сделать двумя способами.

Первый — превратить десятичные дроби в обыкновенные. Например, 1,2 — это то же самое, что 1 2 /₁₀, или 12 /₁₀ в виде неправильной дроби, или 6 /₅ — если её сократить. Соответственно, процесс деления будет выглядеть так:

Теперь осталось перевести обыкновенную дробь обратно в десятичную. Для этого нужно умножить её на такое число, чтобы знаменатель получился кратным 10: 10, 100, 1 000 и так далее. В данном случае 4 /₅ умножаем на 2. Мы получим 8 /₁₀. Добавляем к этому нашу целую часть — 4 — и получаем итоговый результат 4,8.

Второй способ деления десятичных дробей — сначала превратить их в целые числа, а потом поставить запятую в получившемся результате.

• Найдите дробь, в которой больше всего знаков после запятой.
• Умножьте все дроби в примере на число, кратное 10, с таким же количеством нулей. Например, если у вас есть дробь 4,25 — это будет 100, а если 1,578 — 1 000.
• Разделите целые числа друг на друга столбиком.
• Отсчитайте слева направо столько знаков, сколько было добавлено нулей при умножении, и поставьте запятую.

Например: 7,44 ÷ 0,4 = (7,44 × 100) ÷ (0,4 × 100) = 744 ÷ 40 = 18,6.

На целое число

Десятичные дроби на целое число делите так же, как и обычные числа, столбиком. Когда в делимом (слева) закончится целая часть, поставьте запятую в частном (справа под чертой). Если делимое не удаётся разделить без остатка, добавляйте к нему нули, пока не получите конечный результат.

Арифметические вычисления. Проценты. Обыкновенные дроби. Действия над обыкновенными дробями.

1º. Натуральные числа – это числа, употребляемые при счете. Множество всех натуральных чисел обозначают N, т.е. N = (1, 2, 3, …).

Дробью называется число, состоящее из нескольких долей единицы. Обыкновенной дробью называется число вида , где натуральное число n показывает, на сколько равных частей разделена единица, а натуральное число m показывает, сколько таких равных частей взято. Числа m и n называют соответственно числителем и знаменателем дроби.

Если числитель меньше знаменателя, то обыкновенная дробь называется правильной; если числитель равен знаменателю или больше него, то дробь называется неправильной. Число, состоящее из целой и дробной частей, называется смешанным числом.

Например, — правильные обыкновенные дроби, — неправильные обыкновенные дроби, 1 — смешанное число.

2º. При выполнении действий над обыкновенными дробями следует помнить следующие правила:

1) Основное свойство дроби. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.

Например, а) ; б) .

Деление числителя и знаменателя дроби на их общий делитель, отличный от единицы, называется сокращением дроби.

2) Чтобы смешанное число представить в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, записать полученную сумму числителем дроби, а знаменатель оставить прежним.

Аналогично любое натуральное число можно записать в виде неправильной дроби с любым знаменателем.

Например, а) , так как ; б) и т.д.

3) Чтобы неправильную дробь записать в виде смешанного числа (т.е. из неправильной дроби выделить целую часть), нужно числитель разделить на знаменатель, частное от деления взять в качестве целой части, остаток — в качестве числителя, знаменатель оставить прежним.

Например, а) , так как 200 : 7 = 28 (ост. 4); б) , так как 20 : 5 = 4 (ост. 0).

4) Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное (НОК) знаменателей этих дробей (оно и будет их наименьшим общим знаменателем), разделить наименьший общий знаменатель на знаменатели данных дробей (т.е. найти дополнительные множители для дробей), умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Например, приведем дроби к наименьшему общему знаменателю:

, , ;

630 : 18 = 35, 630 : 10 = 63, 630 : 21 = 30.

Значит, ; ; .

5) Правила арифметических действий над обыкновенными дробями:

a) Сложение и вычитание дробей с одинаковыми знаменателями выполняется по правилу:

b) Сложение и вычитание дробей с разными знаменателями выполняется по правилу a), предварительно приведя дроби к наименьшему общему знаменателю.

c) При сложении и вычитании смешанных чисел можно обратить их в неправильные дроби, а затем выполнить действия по правилам a) и b),

d) При умножении дробей пользуются правилом:

e) Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

f) При умножении и делении смешанных чисел, их предварительно переводят в неправильные дроби, а затем пользуются правилами d) и e).

3º. При решении примеров на все действия с дробями следует помнить, что сначала выполняются действия в скобках. Как в скобках, так и вне их сначала выполняют умножение и деление, а затем сложение и вычитание.

Рассмотрим выполнение вышеизложенных правил на примере.

Пример 1. Вычислить: .

1) ;

2) ;

3) ;

4) ;

5) . Ответ: 3.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9460 — | 7447 — или читать все.

78.85.5.224 studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock! и обновите страницу (F5)очень нужно

Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.

Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.

Полезные советы и выводы

Для удобства выполнения операций с дробями с целым числом, рекомендуется использовать правильные дроби вместо смешанных чисел.
При умножении дроби на натуральное число необходимо умножать знаменатель, это поможет корректно выполнить операцию.
Необходимо уметь выполнять преобразование смешанной дроби в неправильную и наоборот, так как это может понадобиться при выполнении различных математических операций.
Важно находить общие знаменатели при сложении или вычитании смешанных чисел для получения корректного результата.
Регулярное выполнение упражнений поможет закрепить знания и навыки по работе с дробями с целым числом.

В данной статье мы рассмотрели различные методы работы с дробями с целым числом и дали подробные пошаговые инструкции по каждому методу. Эти знания будут полезны при выполнении задач и решении математических проблем, связанных с дробями. Практикуйтесь, чтобы закрепить полученные навыки и ощутить уверенность в решении подобных задач.

Как записать обыкновенную дробь в виде бесконечной десятичной дроби

Когда мы хотим записать обыкновенную дробь в виде бесконечной десятичной дроби, мы можем следовать нескольким шагам.

Первый шаг — записать натуральное число, которое получится из дроби, если мы просто игнорируем запятую и скобки. Это число будет являться числителем искомой десятичной дроби.

Затем, второй шаг — записать натуральное число, составленное из цифр, которые стоят перед периодом десятичной дроби. Это число будет являться знаменателем искомой десятичной дроби.

И, наконец, вычисляем разность между этими двумя числами, которая будет числителем искомой обыкновенной дроби.

Таким образом, мы можем записать обыкновенную дробь в виде бесконечной десятичной дроби, следуя этим шагам.

Как понять где ставить запятую в десятичной дроби

Правильное расстановка запятых в десятичной дроби может вызывать затруднения у многих людей. Однако есть простой способ понять, где ставить запятую. Сначала записываем дроби, которые нужно перемножить, в столбик. Затем умножаем эти дроби между собой, как если бы это были обыкновенные числа. После этого считаем количество знаков после запятой у каждой дроби и складываем их. Полученную сумму знаков перемещаем справа налево и ставим запятую. Например, у нас есть дроби 0,5 и 0,3. У первой дроби один знак после запятой, а у второй — ноль. Сложив эти числа, мы получаем 1. Перемещаем это число справа налево и получаем 0,01. Итак, правильное расстановка запятых в данном случае будет 0,01.

Как не целое число перевести в дробь

Для примера рассмотрим число 0.625, которое нужно перевести в десятичную дробь по правилам задания. У нас в основании системы счисления будет число 10, так как переводим в десятичную систему.

Умножим дробную часть числа на 10. Получим 6.25. Записываем целую часть — число 6. Умножаем дробную часть 0.25 на 10 и получаем число 2.5. Записываем целую часть — число 2. Последнее умножение даст нам 5.

Итак, результатом перевода числа 0.625 в десятичную дробь будет 0.625 = 0.625.

Основание системы счисления можно выбирать любым, в зависимости от поставленной задачи. В данном примере было выбрано основание 10, так как речь идет о переводе числа в десятичную дробь.

Как перевести десятичную дробь в целое число

Если десятичная дробь не содержит целой части, то ее переводят в обыкновенную дробь. Для этого числительом становится часть числа после запятой, а знаменатель равен единице, сдвинутой вправо на количество разрядов после запятой. Например, 0,3 = 3/10, а 0,125 = 125/1000. Десятичную дробь также можно записывать в виде десятичной обыкновенной дроби, в которой знаменатель является степенью десяти. Например, 0,3 = 3/10, а 0,125 = 125/1000. Чтобы перевести десятичную дробь в целое число, необходимо умножить ее на 10 столько раз, сколько разрядов в ее дробной части, и округлить результат до целого числа. Например, 3,2 = 32, 0,75 = 7,5. Это позволяет представить десятичную дробь в виде целого числа без фракционной части.