Формулы и правила дифференцирования в математике с примерами решения и образцами выполнения

Модель и функция потерь

При обучении любой модели мы подбирали идеальные веса. Если это модель линейной регрессии (linear regression model) с одним признаком (одной независимой переменной), то наше уравнение может выглядеть следующим образом (постоянный коэффициент или сдвиг мы пока опустим для простоты).

$$ y = w \times x $$

Для того чтобы подобрать вес w у нас есть ещё одна функция, называемая функцией потерь (loss function). Это наш критерий качества первой, основной модели.

$$ MSE = \frac {1}{n} \sum^{n}_{i=1} (y_i-\hat{y}_i) ^2 $$

Напомню, в данном случае мы находим или MSE, которая показывает среднее расстояние всех точек до линии регрессии.

Для того чтобы сделать более очевидной связь функции потерь с исходной моделью мы можем переписать ее следующим образом.

$$ MSE = \frac {1}{n} \sum^{n}_{i=1} (y_i-(w \times x_i))^2 $$

Подставляя наши данные (x_i) и веса (w) и сравнивая результат с целевым значением (y_i), мы будем на каждой итерации получать определенный уровень ошибки.

Графически, модель регрессии — это прямая, функция потерь — парабола. Представим, что в упрощенном виде, эти функции выглядят следующим образом.

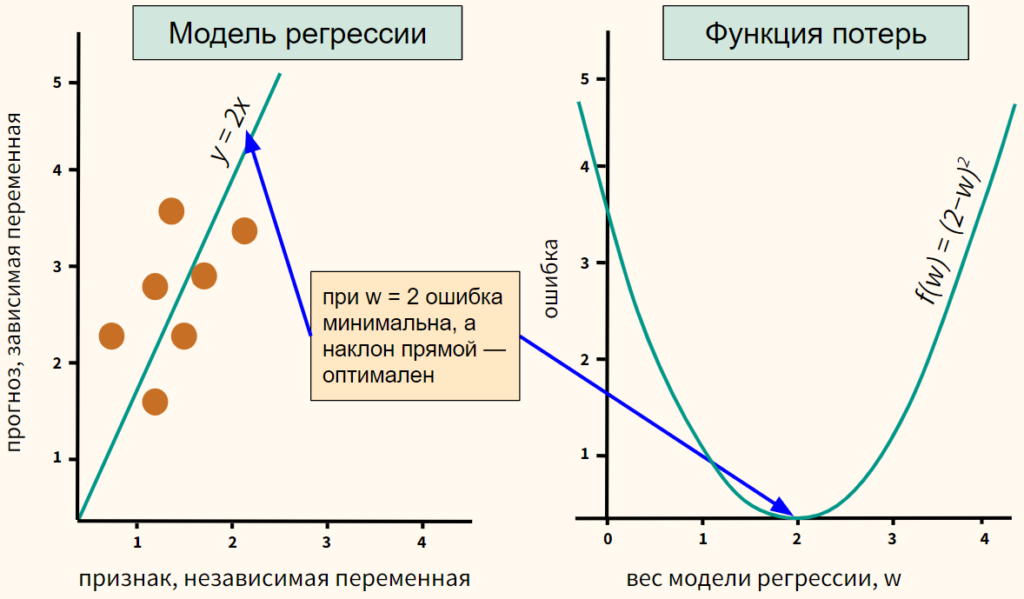
Как они связаны? Там где при определенном весе w значение функции потерь (т.е. ошибка) минимально, вес (а значит и наклон прямой) основной функции оптимален. Из графика очевидно, что идеальным весом с минимальной ошибкой, а значит и наклоном линии регрессии будет w = 2.

Как же найти эту точку? Ведь графики — это просто иллюстрация и никакого надежного метода мы пока не придумали.

«Распаковка» сложной функции

Посмотри на предыдущую функцию еще раз. Сможешь ли ты разобраться в последовательности «упаковки»? Во что икс запихнули сначала, во что потом и так далее до самого конца. То есть — какая функция вложена в какую? Возьми листок и запиши, как ты считаешь. Можно сделать это цепочкой со стрелками как мы писали выше или любым другим способом.

Сделал?

Теперь правильный ответ: сначала икс «упаковали» в \(4\)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию \(2\), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

Например, вот такая функция: \(y=tg⁡(\log_2⁡x )\). Смотрим на икс – что с ним происходит сначала? Берется логарифм от него. А потом? Берется тангенс от результата. Вот и последовательность будет такая же:

\(x → \log_2⁡x → tg⁡(\log_2⁡x )\)

Еще пример: \(y=\cos⁡{(x^3 )}\). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: \(x → x^3 → \cos⁡{(x^3 )}\)

Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть \(\cos⁡{(x·x·x)})\), а там в кубе косинус \(x\) (то есть, \(\cos⁡x·\cos⁡x·\cos⁡x\)). Эта разница возникает из-за разных последовательностей «упаковки»

Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): \(y=\sin⁡{(2x+5)}\). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: \(x → 2x+5 → \sin⁡{(2x+5)}\). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки»

Давай немного углубимся в эту тонкость

И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Как я уже говорил выше, в простых функциях икс «упаковывается» один раз, а в сложных — два и более. При этом любая комбинация простых функций (то есть их сумма, разность, умножение или деление) — тоже простая функция. Например, \(x^7\) – простая функция и \(ctg x\) — тоже. Значит и все их комбинации являются простыми функциями:

\(x^7+ ctg x\) — простая, \(x^7· ctg x\) – простая, \(\frac{x^7}{ctg x}\) – простая и т.д.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:    \(y=cos{⁡(sin⁡x)}\)    \(y=5^{x^7}\)    \(y=arctg⁡{11^x}\)    \(y=log_2⁡(1+x)\) Ответы опять в конце статьи.

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike

«>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

(f

· g

) ’ = f

’ · g

+ f

· g

’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Функция f

(x

) представляет собой произведение двух элементарных функций, поэтому все просто:

f

’(x

) = (x

3 · cos x

)’ = (x

3)’ · cos x

+ x

3 · (cos x

)’ = 3x

2 · cos x

+ x

3 · (− sin x

) = x

2 · (3cos x

− x

· sin x

)

У функции g

(x

) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g

(x

) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g

’(x

) = ((x

2 + 7x

− 7) · e

x

)’ = (x

2 + 7x

− 7)’ · e

x

+ (x

2 + 7x

− 7) · (e

x

)’ = (2x

+ 7) · e

x

+ (x

2 + 7x

− 7) · e

x

= e

x

· (2x

+ 7 + x

2 + 7x

−7) = (x

2 + 9x

) · e

x

= x

(x

+ 9) · e

x

.

Ответ:f

’(x

) = x

2 · (3cos x

− x

· sin x

);g

’(x

) = x

(x

+ 9) · e

x

.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию

А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Если есть две функции f

(x

) и g

(x

), причем g

(x

) ≠ 0 на интересующем нас множестве, можно определить новую функцию h

(x

) = f

(x

)/g

(x

). Для такой функции тоже можно найти производную:

Неслабо, да? Откуда взялся минус? Почему g

2 ? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:

По традиции, разложим числитель на множители — это значительно упростит ответ:

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f

(x

) = sin x

и заменить переменную x

, скажем, на x

2 + ln x

. Получится f

(x

) = sin (x

2 + ln x

) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f

’(x

) = f

’(t

) · t

’, если x

заменяется на t

(x

).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Заметим, что если в функции f

(x

) вместо выражения 2x

+ 3 будет просто x

, то получится элементарная функция f

(x

) = e

x

. Поэтому делаем замену: пусть 2x

+ 3 = t

, f

(x

) = f

(t

) = e

t

. Ищем производную сложной функции по формуле:

f

’(x

) = f

’(t

) · t

’ = (e

t

)’ · t

’ = e

t

· t

’

А теперь — внимание! Выполняем обратную замену: t

= 2x

+ 3. Получим:

f

’(x

) = e

t

· t

’ = e

2x

+ 3 · (2x

+ 3)’ = e

2x

+ 3 · 2 = 2 · e

2x

+ 3

Теперь разберемся с функцией g

(x

). Очевидно, надо заменить x

2 + ln x

= t

. Имеем:

g

’(x

) = g

’(t

) · t

’ = (sin t

)’ · t

’ = cos t

· t

’

Обратная замена: t

= x

2 + ln x

. Тогда:

g

’(x

) = cos (x

2 + ln x

) · (x

2 + ln x

)’ = cos (x

2 + ln x

) · (2x

+ 1/x

).

Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.

Ответ:f

’(x

) = 2 · e

2x

+ 3 ;g

’(x

) = (2x

+ 1/x

) · cos (x

2 + ln x

).

Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.

Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:

(x

n

)’ = n

· x

n

− 1

Немногие знают, что в роли n

вполне может выступать дробное число. Например, корень — это x

0,5 . А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.

Для начала перепишем корень в виде степени с рациональным показателем:

f

(x

) = (x

2 + 8x

− 7) 0,5 .

Теперь делаем замену: пусть x

2 + 8x

− 7 = t

. Находим производную по формуле:

f

’(x

) = f

’(t

) · t

’ = (t

0,5)’ · t

’ = 0,5 · t

−0,5 · t

’.

Делаем обратную замену: t

= x

2 + 8x

− 7. Имеем:

f

’(x

) = 0,5 · (x

2 + 8x

− 7) −0,5 · (x

2 + 8x

− 7)’ = 0,5 · (2x

+ · (x

2 + 8x

− 7) −0,5 .

Наконец, возвращаемся к корням:

Приводится доказательство формулы производной сложной функции. Подробно рассмотрены случаи, когда сложная функция зависит от одной и двух переменных. Производится обобщение на случай произвольного числа переменных.

Здесь мы приводим вывод следующих формул для производной сложной функции. Если ,
то.
Если ,
то.
Если ,
то.

Таблица производных.

В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.

Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)

Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.

	Функция y	Производная функции y y’
1	C   (постоянная величина)	C’ = 0
2	x	x’ = 1
3	xn   (n — любое число)	(xn)’ = nxn-1
x2   (n = 2)	(x2)’ = 2x
4	sin x	(sin x)’ = cosx
cos x	(cos x)’ = — sin x
tg x
ctg x
5	arcsin x
arccos x
arctg x
arcctg x
4	ax
ex
5	loga x
ln x     (a = e)

Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть

Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)

Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…

Рассмотрим несколько примеров:

1. Найти производную функции y = x3

Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:

(x3)’ = 3·x3-1 = 3×2

Вот и все дела.

Ответ: y’ = 3×2

2. Найти значение производной функции y = sinx в точке х = 0.

Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.

По табличке находим синус и соответствующую производную:

y’ = (sin x)’ = cosx

Подставляем ноль в производную:

y'(0) = cos 0 = 1

Это и будет ответ.

3. Продифференцировать функцию:

Что, внушает? ) Такой функции в таблице производных и близко нет.

Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает…

Но если увидеть, что наша функция — это косинус двойного угла, то всё сразу налаживается!

Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:

Т.е. наша хитрая функция есть не что иное, как y = cosx. А это — табличная функция. Сразу получаем:

Ответ: y’ = — sin x.

Пример для продвинутых выпускников и студентов:

4. Найти производную функции:

Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:

А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:

Вот и всё. Это будет ответ.

Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.

Задачи на физический смысл производной.

Физический смысл производной заключается в том, что производная выражает скорость протекания процесса, описываемого зависимостью y = f(x).

Это может означать, например, следующее: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени. Если же мы рассматриваем в качестве функции мгновенную скорость автомобиля, то производная задает изменение его ускорения.
Если мы рассматриваем функцию, задающую зависимость объема произведенной продукции от времени, то производная позволит узнать, как изменялась со временем производительность труда на этом предприятии.Если мы рассматриваем электромагнитные волны, то нам могут потребоваться функции, характеризующие изменение со временем электрического и магнитного полей, а также их производные — скорости изменения этих полей, ведь величина магнитного поля пропорциональна скорости изменения электрического поля.И т.п.

Решая конкретные текстовые задачи на скорость процесса с применением производной, следует не забывать о размерностях величин. Если переменная y, заданная функцией f(x) измеряется в некоторых единицах , а её аргумент в единицах , то производная (скорость) измеряется в единицах [y/x].

Задача 6

Материальная точка движется прямолинейно по закону x(t) = 6t2 − 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9с.

Решение

Находим производнуюx'(t) = (6t2 − 48t + 17)’ = 12t − 48. Таким образом мы получили зависимость скорости от времени. Чтобы найти скорость в заданный момент времени, нужно подставить его значение в полученную формулу:x'(t) = 12t − 48.x'(9) = 12·9 − 48 = 60.

Ответ: 60

Замечание: Убедимся, что не ошиблись с размерностью величин. Здесь единица измерения расстояния (функции) = метр, единица измерения времени (аргумента функции) = секунда, следовательно единица измерения производной [x/t] = [м/с], т.е. производная даёт скорость как раз в тех единицах, которые упомянуты в вопросе задачи.

Задача 7

Материальная точка движется прямолинейно по закону x(t) = −t4 + 6t3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.

Решение

Находим производнуюx'(t) = (−t4 + 6t3 + 5t + 23)’ = −4t3 + 18t2 + 5. Подставляем заданный момент времени в полученную формулуx'(3) = −4·33 + 18·32 + 5 = −108 + 162 + 5 = 59.

Ответ: 59

Задача 8

Материальная точка движется прямолинейно по закону x(t) = t2 − 13t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?

Решение

Находим производнуюx'(t) = (t2 − 13t + 23)’ = 2t − 13. Приравниваем скорость, заданную полученной формулой, значению 3 м/с. 2t − 13 = 3. Решив это уравнение, определим в какое время равенство является верным. 2t − 13 = 3. 2t = 3 + 13.t = 16/2 = 8.

Ответ: 8

Задача 9

Материальная точка движется прямолинейно по закону x(t) = (1/3)t3 − 3t2 − 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Решение

Находим производнуюx'(t) = ( (1/3)t3 − 3t2 − 5t + 3 )’ = t2 − 6t − 5. Составляем и уравнение:t2 − 6t − 5 = 2;t2 − 6t − 7 = 0. Это квадратное уравнение, которое можно решить через дискриминант или по теореме Виета. Здесь, на мой взгляд, вторым способом легче: t₁ + t₂ = 6; t₁·t₂ = −7. Легко догадаться, что t₁ = −1; t₂ = 7. В ответ помещаем только положительный корень, т.к. время не может быть отрицательным.

Ответ: 7

Вернуться и повторить решение задач этого типа с графическим заданием условий:

К этой теме также могут быть отнесены задачи на аналитическое нахождение максимума и минимума функции или наибольшего и наименьшего значений функции на отрезке. Они вынесены в отдельное задание профильного уровня. Перейти к этому заданию.

Перейдите по стрелке, чтобы найти ссылки на другие задачи ЕГЭ по математике.

Основные правила дифференцирования

До этого мы рассматривали довольно простые, то есть стандартные функции, для каждой из которых производную можно узнать из справочника или таблицы. Но что делать, если нам потребовалось продифференцировать функцию, которая состоит из нескольких основных? Например, что делать с функциями у = 5х2 + 6х – 3 или у = x•sinx?

Все более сложные функции можно получить из нескольких простых, комбинируя их. Так, функция у = х3 + х2 получается сложением функций у = х3 и у = х2, а функция у = (lnx)•(cosx) – произведением функций у = lnx и у = сosx.

Есть несколько правил, которые позволяют находить производные в таких случаях. Мы не будем их доказывать, а просто дадим их формулировки. Также будем нумеровать правила. Первое из них помогает находить производную сумму функций.

В данном случае u и v – это просто обозначение каких-то произвольных функций. Рассмотрим пример. Пусть надо найти производную функции

Правило работает и в том случае, если сумма представляет собой сумму не двух, а большего числа слагаемых:

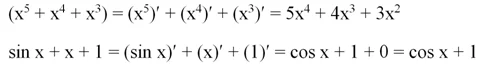
Следующее правило позволяет выносить постоянный множитель за знак производной:

Покажем использование этого правила:

Действительно, зная эти формулы и первые два правила вычисления производных, мы можем записать, что

Задание. Вычислите значение производной функции у = 9х3 + 7х2 – 25х + 7 в точке х = 1.

Решение. Пользуясь правилами дифференцирования, находим производную:

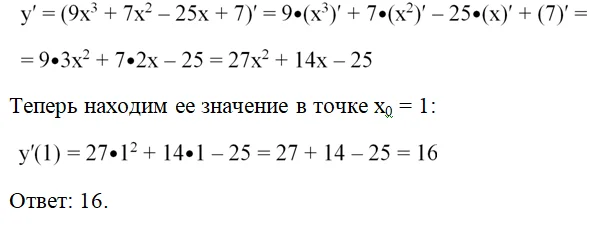
Несколько сложнее обстоит дело с дифференцированием функций, получающихся при перемножении простых функций. В таких случаях используется следующее правило:

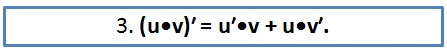
Предположим, надо найти производную для функции у = х2•sinx. Её можно представить как произведение u•v, где

Примечание. В последнем случае мы в конце примера использовали формулу :

Заметим, что иногда одно и то же задание с производной можно решить по-разному, используя или не используя правило для вычисления производной произведения функций.

Задание. Найдите производную функции у = х2•(3х + х3). Вычислите ее значение при х = 1.

Решение. Функция у представляет собой произведение более простых функций u•v, где

Задание. Продифференцируйте функцию

Решение. Здесь перед нами функция, которая представляет собой произведение сразу трех множителей. Что делать в таком случае? Надо всего лишь добавить скобки и их помощью оставить только два множителя (один их них окажется «сложным»):

Довольно сложно выглядит формула для поиска производной дроби:

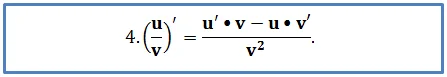
Например, пусть надо найти производную функции

С помощью данного правила можно доказать некоторые равенства. Так, ранее мы уже записали (без доказательства) формулы производных тригонометрических функций:

Оказывается, формула для тангенса может быть выведена из формул для синуса и косинуса. Действительно, тангенс можно записать в виде дроби:

Задание. Найдите, в каких точках надо провести касательную к графику дробно-линейной функции

чтобы эта касательная образовала с осью Ох угол в 135°.

Решение. Угол будет равен 135° только тогда, когда значение производной будет равно (– 1) (так как tg 135° = – 1). Поэтому сначала найдем производную. В данном случае следует использовать правило 4, так как функция у явно записана как дробь:

Получили два значения х. Построив график и проведя касательные, мы убедимся, что они действительно образуют с осью Ох угол 135°:

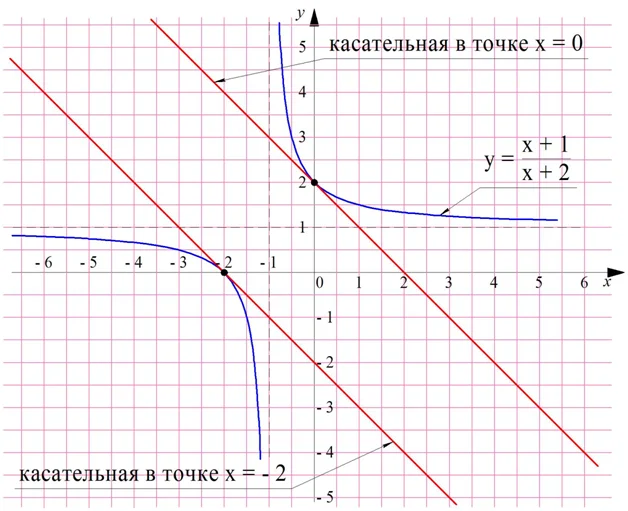
Ответ: – 2 и 0.

Заметим, что иногда можно избавиться от необходимости использовать правило 4, если дифференцируемую функцию можно преобразовать. При этом часто помогает использование отрицательных степеней. Пусть надо продифференцировать функцию

Напрашивается решение использовать правило 4.И такой путь позволит получить правильное решение, хотя и будет несколько трудоемким. Однако можно преобразовать функцию:

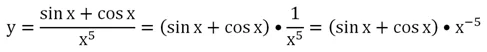
У нас получилось произведение, а потому можно использовать правило 3, которое представляется более простым:

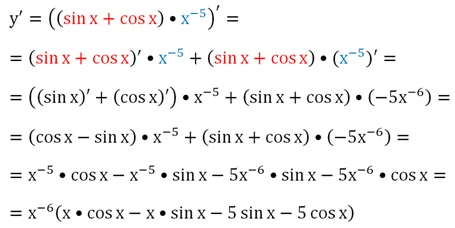
Вывод формул производной функции

Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись \(f(x)\) означает, что функция берется от аргумента \(x\). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента \(x\) может стоять все что угодно, например выражение \(2x+3\). Обозначение такой функции будет \(f(2x+3)\), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента \(x\) мы пишем \(2x+3\).

И несколько важных замечаний про \(\Delta f(x)\) и \(\Delta x\). Напомню, что значок \(\Delta\) означает изменение некоторой величины. \(\Delta x\) — изменения координаты \(x\) при переходе от одной точки на графике функции к другой; \(\Delta f(x)\) — разница координат \(y\) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем \(\Delta x\) для двух близких точек на графике функции \(O\) и \(B\):
$$\Delta x=x_B-x_O;$$
Отсюда можно выразить \(x_B\):
$$x_B=x_O+\Delta x;$$
Абсцисса (координата точки по оси \(x\)) точки \(B\) получается путем сложения абсциссы точки \(O\) и \(\Delta x\).

Кстати, функцию \(f(x)=x^3+sin(x)\) от аргумента \(x_B=x_O+\Delta x\) можно расписать:

Вывод простейших для нахождения производных конкретных функций

При решении задач с элементарными и сложными функциями удобно пользоваться нижеприведенными основными формулами для нахождения их производной.

1. Производная натурального логарифма по x для элементарной функции имеет общий вид .

В случае расчетов со сложными функциями следует воспользоваться формулой .

2. Производная логарифмической функции по основанию a для элементарной функции вычисляется таким образом: 

Если функция сложная, то формула примет следующий вид: 

3. Производная по x в степени n определяется, согласно краткому уравнению .

Когда в решении задачи присутствует сложная функция, можно воспользоваться формулой: 

4. Производная квадратного корня для элементарной функции равна: .

Для сложной функции: .

5. При расчете производной a в степени x нужно использовать формулу , когда функция элементарная.

Используем формулу , когда функция сложная.

6. Производная e в степени x в случае элементарной функции составляет .

Если функция сложная, то формула примет вид: .

7. Производная синуса для элементарной функции равна .

В случае сложной функции значение можно посчитать так: .

8. Производная косинуса для элементарной функции 

Для сложной функции — 

9. Когда требуется определить производную тангенса для элементарной функции, следует воспользоваться формулой: 

Если функция сложная, то подойдет следующая формула: 

10. Вычислить производную котангенса для элементарной функции можно с помощью уравнения .

Для сложной функции — .

11. Формула производной арксинуса имеет вид: 

Если функция сложная, то следует воспользоваться следующей формулой: .

12. Производную арккосинуса для элементарной функции вычисляют таким образом: .

В случае сложной функции формула следующая: .

13. Если требуется вычислить производную арктангенса для элементарной функции, пригодится формула: .

В случае сложной функции следует использовать такую формулу: .

14. Производная арккотангенса для элементарной функции: .

Для сложной функции производную вычисляют следующим образом: .