Каноническое уравнение прямой на плоскости
Определение канонического уравнения — это уравнение следующего вида \.
Данное уравнение задает на плоскости в прямоугольной системе прямую линию. Она, в свою очередь проходит через точку \, которая имеет вектор направления, обозначающийся как \
Запишем несколько примеров для данного вида уравнения.
\
Приведенное уравнение — это уравнение прямой для канонического вида. Прямая его будет проходить через значения точек \. Вектор направляющий равен \.
Важные моменты, которые следует помнить, при решении задач с каноническим уравнением.
Отметим следующие важные факты:
- если вектор является прямым и прямая линия проходит через точку, то ее уравнение имеет вид : \
- когда вектор прямой по направлению, то любой из векторов может быть направляющим вектором прямой. И уравнение записывается следующим образом: \
Пример №1:
Прямая в системе координат проходит через точки (2;-4) и вектор направляющий равен (1;-3). Составьте и напишите каноническое уравнение, применяя известные нам данные.
\
\
Следовательно уравнение записывается следующим образом: \
\ — окончательное искомое уравнение.
Пример №2:
Составить каноническое уравнение, проходящее через точки \{2} ; \quad-\frac{1}{7}\]
Прямая является параллельной относительно оси координат. Направляющий вектор принимается \. Учитывая значение точек, через которые проходит прямая, записываем уравнение:
\{2}}{0}=\frac{y-\left(-\frac{1}{7}\right)}{1} \Leftrightarrow \frac{x-\sqrt{2}}{0}=\frac{y+\frac{1}{7}}{1}\]
\{2}}{0}=\frac{y+\frac{1}{7}}{1}\]
Пример №3:
Составим уравнение, руководствуясь графиком, приведенным ниже.
Из рисунка видно, что прямая проходит через точки со значениями (0;3). Расположена параллельно относительно оси x (ось абсцисс). Координатный вектор \ — направляющий вектор, для данной системы.
Собрав все данные, преобразовав их. можно записать уравнение:
\
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Нужна помощь
Фракталы
Подробнее об этом виде кривых мы писали тут. Однако в рамках разговора об эволюции представлений о кривых не упомянуть их невозможно. Классическим примером фрактала (фигуры со свойством самоподобия) является кривая Коха.
Свойство самоподобия означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:
В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.
Наш подход с прямыми отрезками терпит здесь фиаско — вместо приближения к какой-то конечной длине сумма длин отрезков неограниченно растет.
Конечно, кривые, обладающие этим свойством, не исчерпываются самоподобными фигурами. Достаточно найти трещину на стене не самой простой формы: самоподобия в ней мы, как правило, не наблюдаем, и в то же время от одной ее «ветки» отходят новые, иной формы, и т. д.
Заполнить плоскость
В 1890 году итальянский математик Джузеппе Пеано построил непрерывную кривую, которая проходит через любую точку квадрата (в оригинале использовался единичный, но построение легко повторить для квадрата любых размеров). Пеано задавался вопросом: может ли кривая заполнить всю плоскость или пространство? Результат Пеано воспринимался контринтуитивно. Годом позже кривую с тем же свойством построил уже графически Давид Гильберт.
В дальнейшем все кривые со свойством «заполнения» квадрата стали называть кривыми Пеано, а в более узком смысле это название закрепилось за конкретной кривой из его статьи 1890 года. Поскольку кривая заполняет любой наперед заданный квадрат, мы можем использовать ее и для заполнения плоскости, а в более общем случае — пространства или пустоты внутри нас.
Уравнение прямой в отрезках. Уравнение прямой в параметрической форме
Уравнение прямой в отрезках имеет вид , где – ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность (так как свободный член равен нулю и единицу в правой части никак не получить).
Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой представить в виде уравнения прямой в отрезках . Чем оно удобно? Уравнение прямой в отрезках позволяет быстронайти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.
Найдём точку пересечения прямой с осью . Обнуляем «игрек», и уравнение принимает вид . Нужная точка получается автоматически: .
Аналогично с осью – точка, в которой прямая пересекает ось ординат.
В математике одним из параметров, описывающих положение прямой на декартовой плоскости координат, является угловой коэффициент этой прямой. Этот параметр характеризует наклон прямой к оси абцисс. Чтобы понять, как найти угловой коэффициент, сначала вспомним общий вид уравнения прямой в системе координат XY.
В общем виде любую прямую можно представить выражением ax+by=c, где a, b и c — произвольные действительные числа, но обязательно a 2 + b 2 ≠ 0.
Подобное уравнение с помощью несложных преобразований можно довести до вида y=kx+d, в котором k и d — действительные числа. Число k является угловым коэффициентом, а само уравнение прямой подобного вида называется уравнением с угловым коэффициентом. Получается, что для нахождения углового коэффициента, необходимо просто привести исходное уравнение к указанному выше виду. Для более полного понимания рассмотрим конкретный пример:
Задача: Найти угловой коэффициент линии, заданной уравнением 36x — 18y = 108
Решение: Преобразуем исходное уравнение.
Ответ: Искомый угловой коэффициент данной прямой равен 2.
В случае, если в ходе преобразований уравнения мы получили выражение типа x = const и не можем в результате представить y в виде функции x, то мы имеем дело с прямой, параллельной оси Х. Угловой коэффициент подобной прямой равен бесконечности.
Для прямых, которых выражены уравнением типа y = const, угловой коэффициент равняется нулю. Это характерно для прямых, параллельных оси абцисс. Например:
Задача: Найти угловой коэффициент линии, заданной уравнением 24x + 12y — 4(3y + 7) = 4
Решение: Приведем исходное уравнение к общему виду
24x + 12y — 12y + 28 = 4
Из полученного выражения выразить y невозможно, следовательно угловой коэффициент данной прямой равен бесконечности, а сама прямая будет параллельна оси Y.
Как установить соответствие между графиками и функциями прямых?
1. Определить тип прямой по графику
Первый шаг для установления соответствия между графиками и функциями прямых — понять тип прямой по ее графику. Для определения типа прямой надо проследить, как она движется по координатной плоскости. Если она убывает слева направо, то это прямая с отрицательным наклоном, а если растет, значит, ее наклон положителен. Горизонтальная прямая имеет наклон равный 0, а вертикальная — бесконечный.
2. Записать уравнение прямой по точке на графике
Зная тип прямой, можно записать ее уравнение. Для этого надо определить координаты одной из точек на графике и угловой коэффициент — отношение изменения координаты по оси y к изменению координаты по оси x. Он равен тангенсу угла между прямой и положительным направлением оси x. С учетом этого определяется величина сдвига прямой по оси y.
3. Сравнить уравнение прямой с вариантами функций
После получения уравнения прямой необходимо сравнить его с вариантами функций. Функция обычно записывается в виде y=f(x), где y — переменная, зависящая от x. При этом в уравнение прямой вместо y подставляется константа, а вместо x — переменная.
4. Использовать график функции для проверки
Для проверки, правильно ли установлено соответствие между графиками и функциями прямых, можно использовать график функции. Если при подстановке значений x функция выдаст необходимые значения y, соответствие установлено правильно. Если же результаты не совпадают, надо еще раз проверить уравнение прямой и ее график, чтобы найти ошибку.
Вычисление уравнения прямой
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х\ параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол
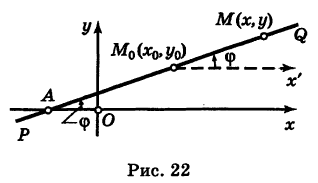
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
![]()
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
![]()

![]()
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Шаг 5: Практические примеры
Пример 1
На графике представлена функция y = 2x — 1. Найдём её коэффициенты и установим соответствие с прямой:
- Наклон прямой: 2 (коэффициент перед х в формуле функции);
- Свободный член: -1 (константа в формуле функции).
Таким образом, можно заключить, что график функции y = 2x — 1 соответствует прямой, которая проходит через точку (0, -1) и имеет угол наклона 45°.
Пример 2
Рассмотрим график функции y = -0.5x + 3. Для установления соответствия с прямой определим коэффициенты:
- Наклон прямой: -0.5 (коэффициент перед х в формуле функции);
- Свободный член: 3 (константа в формуле функции).
Полученные значения позволяют установить, что график функции y = -0.5x + 3 соответствует прямой, которая проходит через точку (0, 3) и имеет угол наклона 26.57°.
Пример 3
Последний пример — это график функции y = x. Он соответствует прямой, которая является 45-градусной прямой пересечения сетки координат. Таким образом, угол наклона равен 45°, а точка пересечения с обеими осями координат — это начало координат (0, 0).
Что такое теоретические методы исследования
Теоретическими методами исследования называют методики, разработанные с целью определить задачи, создать гипотезы, оценить полученные прецеденты.
Теоретические методы выступают в противовес эмпирическому уровню исследований и предусматривают погружение в суть изучаемого объекта или явления с целью понять его внутреннюю структуру, причины и источники появления, а также систему, согласно которой он формируется и функционирует. Основные задачи, которые решаются в процессе применения методик:
- установить прецеденты;
- определить внешние связи между изучаемыми объектами и явлениями;
- подробно объяснить причины возникновения, смысл существования.
Теоретические методы тесно взаимодействуют с мыслительной деятельностью, связаны с процессами осмысления эмпирического материала, его доработкой и анализом. Назначением исследовательской работы является раскрытие внутренней структуры систем или явлений, определение их взаимосвязи и обусловленности.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем
уравнение прямой, проходящей через
заданную точку Мо (х О;
у о)
перпендикулярно данному ненулевому
вектор n = (А; В).
Возьмем
на прямой произвольную точку М(х; у) и
рассмотрим вектор М 0 М
(х — х 0 ;
у — у о)
(см. рис.1). Поскольку векторы n и М о М
перпендикулярны, то их скалярное
произведение равно нулю: то есть
А(х
— хо) + В(у — уо) = 0.
(10.8)
Уравнение
(10.8) называется уравнением
прямой, проходящей через заданную точку
перпендикулярно заданному вектору
.
Вектор
n= (А; В), перпендикулярный прямой,
называется нормальным нормальным
вектором этой прямой
.
Уравнение
(10.8) можно переписать в виде Ах
+ Ву + С =0
,
(10.9)
где
А и В координаты нормального вектора,
С = -Ах о
— Ву о
— свободный член. Уравнение (10.9) есть
общее уравнение прямой
(см. рис.2).
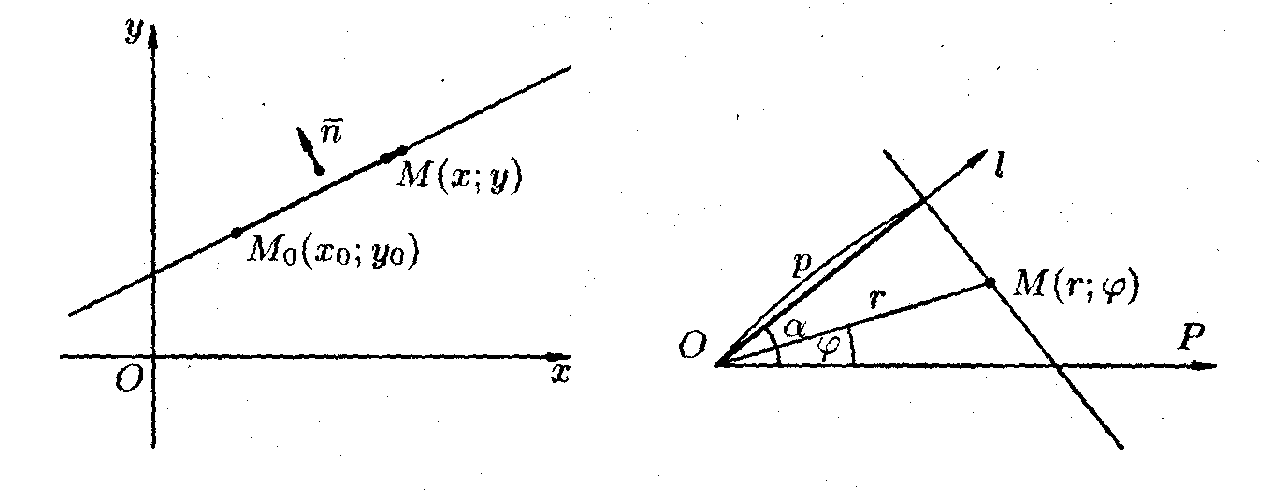
Рис.1
Рис.2
Понятие линейной регрессии. Парная линейная регрессия
Линейная регрессия — выраженная в виде прямой зависимость среднего значения какой-либо
величины от некоторой другой величины. В отличие от функциональной зависимости ,
когда каждому значению независимой переменной x соответствует одно определённое значение
величины y, при линейной регрессии одному и тому же значению x могут соответствовать
в зависимости от случая различные значения величины y.
Если в результате наблюдения установлено,
что при каждом определённом значении x существует сколько-то (n) значений переменной
y, то зависимость средних арифметических значений y от x и является регрессией
в статистическом понимании.

Если установленная зависимость может быть записана в виде уравнения прямой
,
то эта регрессионная зависимость называется линейной регрессией.
О парной линейной регрессии говорят, когда установлена зависимость между двумя
переменными величинами (x и y). Парная линейная регрессия называется также однофакторной
линейной регрессией, так как один фактор (независимая переменная x) влияет на результирующую
переменную (зависимую переменную y).
В уроке о корреляционной зависимости
были разобраны примеры того, как цена на квартиры зависит от общей площади квартиры и от площади
кухни (две различные независимые переменные) и о том, что результаты наблюдений расположены в некотором
приближении к прямой, хотя и не на самой прямой. Если точки корреляционной диаграммы соединить ломанной
линией, то будет получена линия эмпирической регрессии. А если эта линия будет выровнена в прямую, то
полученная прямая будет прямой теоретической регрессии. На рисунке ниже
она красного цвета (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши).
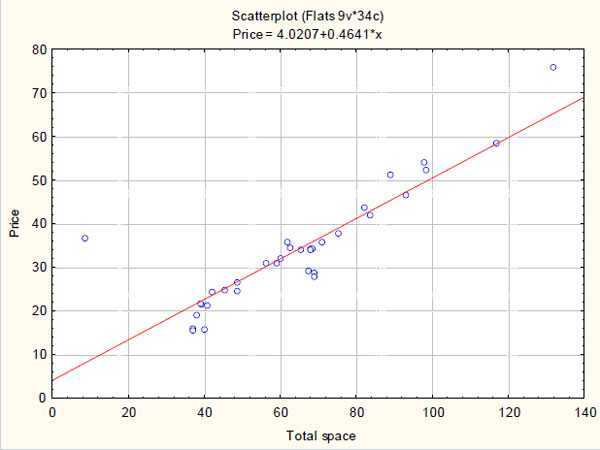
По этой прямой теоретической регрессии может быть сделан прогноз или восстановление
неизвестных значений зависимой переменной по заданным значениям независимой переменной.
В случае парной линейной регрессии для данных генеральной совокупности связь между
независимой переменной (факториальным признаком) X и зависимой переменной (результативным
признаком) Y описывает модель
,
где
—
свободный член прямой парной линейной регрессии,
—
коэффициент направления прямой парной линейной регрессии,
—
случайная погрешность,
N — число элементов генеральной совокупности.
Уравнение парной линейной регрессии для генеральной совокупности можно построить, если
доступны данные обо всех элементах генеральной совокупности. На практике данные всей генеральной совокупности
недоступны, но доступны данные об элементах некоторой выборки.
Поэтому параметры генеральной совокупности оценивают при помощи соответствующих
параметров соответствующей выборки: свободный член прямой парной линейной регрессии генеральной совокупности
заменяют на
свободный член прямой парной линейной регрессии выборки ,
а коэффициент направления прямой парной линейной регрессии генеральной совокупности
— на коэффициент
направления прямой парной линейной регрессии выборки
.
В результате получаем уравнение парной линейной регрессии выборки
или
где
—
оценка полученной с помощью модели линейной регрессии зависимой переменной Y,
—
погрешность,
n — размер выборки.
Чтобы уравнение парной линейной регрессии было более похоже на привычное уравнение
прямой, его часто также записывают в виде
.
Значение векторного типа
Все разновидности примеров в геометрии тесно связаны друг с другом. В качестве основы для них выступает векторное уравнение, так как именно оно следует из определённой прямой. Для примера можно рассмотреть ситуацию, когда в пространстве дана точка Y (t0, e0, x0). По условиям известно, что она принадлежит прямой. В этом случае можно провести бесконечное количество линий.
Для проведения единственной прямой следует правильно задать направление, которое определяется вектором. Для обозначения можно задействовать v (a, b, c). Символы в скобках являются координатами. Для всех точек W (s, z, m), которые расположены на конкретной прямой, можно написать логическое равенство: (s, z, m) = (t0, e0, x0) + а*v— (a, b, c).

В приведённом примере был взят символ а, который может принимать любое значение. Если попробовать умножить вектор на определённое число, то в итоге можно будет изменить не только первоначальный модуль, но и направление. Это равенство принято называть векторным уравнением для прямой в трёхмерном пространстве. Если правильно оперировать параметром а, то в итоге можно получить все точки (s, z, m), которые сформируют одну линию.
Направляющим принято называть стоящий в уравнении вектор v— (a, b, c). Длина прямой бесконечна, к тому же она не имеет чёткого направления. Все эти факторы означают, что абсолютно любой вектор, который был получен из v- при помощи умножения на действительное число, тоже будет выступать в роли направляющей для прямой.
Если нужно определиться с точкой Y (t0, e0, x0), то в качестве примера вместо неё можно задействовать произвольную точку, которая лежит на прямой. Когда приведённый пример сопоставить с двухмерной реальностью, можно будет получить следующую формулу: (s, z) = (t0, e0) + а * (a; b). Результат практически идентичен с предыдущим случаем, но только в этой ситуации применяются две координаты вместо привычных трёх для указания всех векторов и точек.
Как составить уравнение прямой по двум точкам: двумерный и трехмерный случаи
Прямая в геометрии является одним из самых важных элементов, поскольку из нее собираются многие фигуры как на плоскости, так и в пространстве. Достаточно назвать треугольник, параллелограмм, призму, пирамиду — все они образованы пересекающимися прямыми. В данной статье дан ответ на вопрос, как по двум точкам составить уравнение прямой.
Уравнение прямой для двумерного и трехмерного случаев
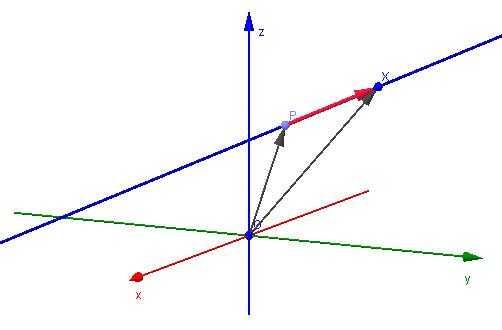
Прежде чем переходить к обсуждению вопроса, как по двум точкам составить уравнение прямой, следует понять, о чем идет речь.
Под уравнением прямой понимают равенство, связанное с принятой системой координат, причем все значения переменных, удовлетворяющие ему, должны ложиться на одну прямую. В двумерном и трехмерном случаях это уравнение можно задать в следующем виде:
Здесь Q — координаты произвольной точки прямой, P — координаты конкретной точки, принадлежащей прямой, u¯ — направляющий вектор, α — любое действительное число. Направляющий вектор u¯ является параллельным прямой. Это выражение называется параметрически-векторным уравнением.
В двумерном случае каждая точка на плоскости однозначно задается двумя координатами x и y, поэтому можно записать уравнение прямой в виде:
Где (x0; y0) — координаты известной точки прямой, (a; b) — координаты направляющего вектора. В параметрическом виде это уравнение можно переписать как систему из двух уравнений:
Выражая параметр альфа и приравнивая полученные равенства, приходим к виду:
Полученное выражение знакомо каждому школьнику. Оно называется общим уравнением прямой на плоскости.
В пространстве каждая точка задана не двумя, а тремя координатами, поэтому ее уравнение параметрически-векторное принимает форму:
Параметрически-векторное уравнение удобно использовать, когда нужно составить уравнение прямой, проходящей через две точки.
Прямая и две точки
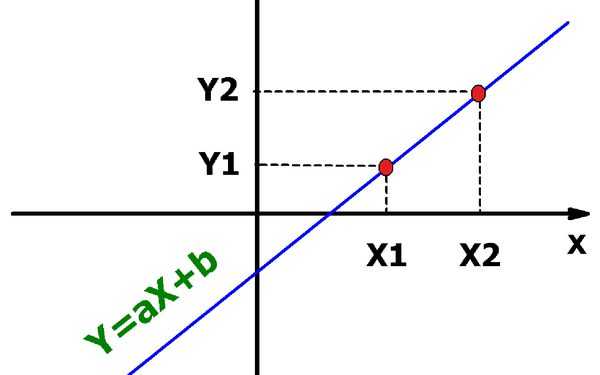
Теперь рассмотрим непосредственно вопрос статьи. Как по двум точкам составить прямой уравнение? Сначала получим уравнение на плоскости, а затем обобщим его для трехмерного случая.
Предположим, что имеется две точки на плоскости P(x1; y1) и Q(x2; y2). Если взять разность координат точек, то мы получим вектор, который направлен от одной из них к другой. Этот вектор равен:
В данном случае PQ¯ направлен от P (начало направленного отрезка) к Q (его конец). Поскольку обе точки принадлежат прямой, то и вектор PQ¯ принадлежит ей. Это означает, что его можно считать направляющим. Уравнение прямой принимает вид:
Здесь мы взяли точку P. Если ее заменить точкой Q, то уравнение не изменится.
Как по двум точкам составить уравнение прямой в пространстве? Обобщая полученную формулу для плоскости, получаем:
Другая буква для параметра взята чтобы показать независимость этого и предыдущего уравнений.
Пример решения задачи
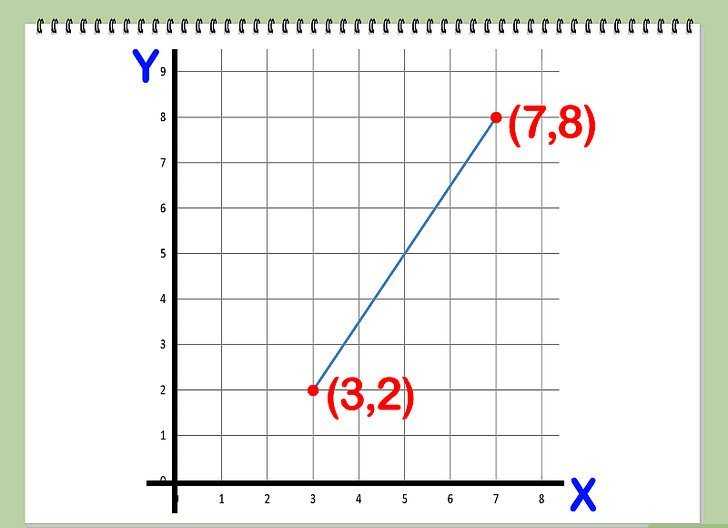
Разобравшись, как составить прямой уравнение по двум точкам, приведем пример использования полученных знаний для двумерного случая.
Пусть имеются точки на плоскости (3; -4) и (0; 7). Необходимо составить через две точки прямой уравнение.
Вычисляем координаты направляющего вектора:
Параметрически-векторное уравнение имеет вид:
Раскроем его и приведем к общему виду:
Мы получили уравнение в привычном (общем) виде. Можно проверить его справедливость, подставив координаты обеих точек из условия задачи.
Примеры
Две прямые заданы уравнениями. Найти точку пересечения этих прямых и углы под которым они пересекаются
line_p A=11;B=-5;C=6,k=3/7;b=-5
Получаем следующий результат
Уравнение первой прямой
y = 2.2 x + (1.2)
Уравнение второй прямой
y = 0.4285714285714 x + (-5)
Угол пересечения двух прямых(в градусах)
-42.357454705937
Точка пересечения двух прямых
x = -3.5
y = -6.5

Не забудьте что параметры двух линий разделяются запятой, а параметры каждой линии точкой с запятой.
Прямая проходит через две точки (1:-4) и (5:2) . Найти уравнение прямой, которая проходит через точку (-2:-8) и пересекает исходную прямую под углом 30 градусов.
Одна прямая нам известна, так как известны две точки через которые она проходит.
Осталось определить уравнение второй прямой. Одна точка нам известна, а вместо второй указан угол, под которым первая прямая пересекает вторую.
Вроде все известно, но тут главное не ошибится. Речь идет об угле(30 градусов) не между осью абсцисс и линией, а между первой и второй линией.
Для этого мы постим так. Определим параметры первой линии, и узнаем под каким углом она пересекает ось абсцисс.
line xa=1;xb=5;ya=-4;yb=2
Общее уравнение Ax+By+C = 0
Коэффициент А = -6
Коэффициент B = 4
Коэффициент C = 22
Коэффициент a= 3.6666666666667
Коэффициент b = -5.5
Коэффициент k = 1.5
Угол наклона к оси (в градусах) f = 56.309932474019
Коэффициент p = 3.0508510792386
Коэффициент q = 2.5535900500422
Расстояние между точками=7.211102550928
Видим что первая линия пересекает ось под углом 56.309932474019 градусов.
В искходных данных не сказано как именно пересекает вторая линия, первую. Можно ведь построить две линии удовлетворяющих условиям, первая повернутая на 30 градусов ПО часовой стрелке, а вторая на 30 градусов ПРОТИВ часовой стрелке.
Давайте их и посчитаем
Если вторая линия повернута на 30 градусов ПРОТИВ часовой стрелке, то вторая линия будет иметь градус пересечения с осью абсцисс 30+56.309932474019 = 86
.309932474019
градусов
line_p xa=-2;ya=-8;f=86.309932474019
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C = 0
Коэффициент А = 23.011106998916
Коэффициент B = -1.4840558255286
Коэффициент C = 34.149767393603
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a= -1.4840558255286
Коэффициент b = 23.011106998916
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k = 15.505553499458
Угол наклона к оси (в градусах) f = 86.309932474019
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p = -1.4809790664999
Коэффициент q = 3.0771888256405
Расстояние между точками=23.058912962428
Расстояние от точки до прямой li =
то есть наше уравнение второй линии есть y=15.505553499458x
+
23.011106998916
Пусть даны две прямые и требуется найти их точку пересечения. Так как эта точка принадлежит каждой из двух данных прямых, то ее координаты должны удовлетворять как уравнению первой прямой, так и уравнению второй прямой.
Таким образом, для того чтобы найти координаты точки пересечения двух прямых, следует решить систему уравнений
Пример 1. Найти точку пересечения прямых и
Решение. Координаты искомой точки пересечения мы найдем, решив систему уравнений
Точка пересечения М имеет координаты
Покажем, как построить прямую по ее уравнению. Для построения прямой достаточно знать две ее точки. Чтобы построить каждую из этих точек, мы задаемся произвольным значением одной из ее координат, а затем из уравнения находим соответствующее значение другой координаты.
Если в общем уравнении прямой оба коэффициента при текущих координатах не равны нулю , то для построения этой прямой лучше всего находить точки ее пересечения с осями координат.
Пример 2. Построить прямую .
Решение. Находим точку пересечения данной прямой с осью абсцисс. Для этого решаем совместно их уравнения:
и получаем . Таким образом, найдена точка М (3; 0) пересечения данной прямой с осью абсцисс (рис. 40).
Решая затем совместно уравнение данной прямой и уравнение оси ординат
мы находим точку пересечения прямой с осью ординат. Наконец, строим прямую по ее двум точкам М и
В двумерном пространстве две прямые пересекаются только в одной точке, задаваемой координатами (х,y). Так как обе прямые проходят через точку их пересечения, то координаты (х,y) должны удовлетворять обоим уравнениям, которые описывают эти прямые. Воспользовавшись некоторыми дополнительными навыками вы сможете находить точки пересечения парабол и других квадратичных кривых.
Анализ качества модели линейной регрессии
Метод наименьших квадратов имеет по меньшей мере один существенный недостаток: с его
помощью можно найти уравнение линейной регрессии и в тех случаях, когда данные наблюдений значительно
рассеяны вокруг прямой регрессии, то есть находятся на значительном расстоянии от этой прямой. В таких
случаях за точность прогноза значений зависимой переменной ручаться нельзя. Существуют показатели,
которые позволяют оценить качество уравнения линейной регрессии прежде чем использовать модели линейной
регрессии для практических целей. Разберём важнейшие из этих показателей.
Коэффициент детерминации
Коэффициент детерминации
принимает значения от 0 до 1 и в случае качественной модели линейной регрессии стремится к единице.
Коэффициент детерминации показывает, какую часть общего рассеяния зависимой переменной объясняет независимая переменная:
,
где
—
сумма квадратов отклонений, объясняемых моделью линейной регрессии, которая характеризует рассеяние
точек прямой регрессии относительно арифметического среднего,
—
общая сумма квадратов отклонений, которая характеризует рассеяние зависимой переменной Y
относительно арифметического среднего,
—
сумма квадратов отклонений ошибки (не объясняемых моделью линейной регрессии), которая характеризует
рассеяние зависимой переменной Y относительно прямой регресии.
Пример 3. Даны сумма квадратов отклонений, объясняемых моделью линейной
регрессии (3500), общая сумма квадратов отклонений (5000) и сумма квадратов отклонений ошибки (1500).
Найти коэффициент детерминации двумя способами.
F-статистика (статистика Фишера) для проверки качества модели линейной регрессии
Минимальное возможное значение F-статистики — 0. Чем выше значение статистики Фишера,
тем качественнее модель линейной регрессии. Этот показатель представляет собой отношение объясненной
суммы квадратов (в расчете на одну независимую переменную) к остаточной сумме квадратов (в расчете на
одну степень свободы):
где m — число объясняющих переменных.
Сумма квадратов остатков
Сумма квадратов остатков (RSS) измеряет необъясненную часть дисперсии
зависимой переменной:
где
—
остатки — разности между реальными значениями зависимой переменной и значениями,
оценёнными уравнением линейной регрессии.
В случае качественной модели линейной регрессии сумма квадратов остатков стремится
к нулю.
Стандартная ошибка регрессии
Стандартная ошибка регрессии (SEE) измеряет величину квадрата ошибки,
приходящейся на одну степень свободы модели:
Чем меньше значение SEE, тем качественнее модель.
Пример 4. Рассчитать коэффициент детерминации для данных из примера 1.
Решение. На основании данных таблицы (она была приведена в примере урока о корреляционной
зависимости) получаем, что ,
, .
Можем убедиться, что выполняется закономерность :
.
Получаем коэффициент детерминации:
.
Таким образом, 83,6% изменений частного потребления можно объяснить моделью линейной
регресии.
Параметрические уравнения прямой и плоскости.
Прямая линия (на плоскости или в пространстве) полностью определена, если на ней задана точка \(M_{0}\) и задан ненулевой вектор \(\boldsymbol{a}\), параллельный этой прямой. Разумеется, и точку, и вектор можно выбрать по-разному, но мы будем считать, что они как-то выбраны, и называть их начальной точкой и направляющим вектором. Аналогично, плоскость задается точкой и двумя неколлинеарными векторами, ей параллельными, — начальной точкой и направляющими векторами плоскости.
Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.
Пусть дана прямая. Обозначим через \(\boldsymbol{r}_{0}\) и \(\boldsymbol{a}\) соответственно радиус-вектор ее начальной точки \(M_{0}\) и направляющий вектор. Рассмотрим некоторую точку \(M\) с радиус-вектором \(\boldsymbol{r}\) (рис. 6.1).
Рис. 6.1
Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда \(M\) также лежит на прямой. В этом и только этом случае для точки \(M\) найдется такое число \(t\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t\boldsymbol{a}.\label{ref3}
$$
Наоборот, какое бы число мы ни подставили в формулу \eqref{ref3} в качестве \(t\), вектор \(\boldsymbol{r}\) в этой формуле определит некоторую точку на прямой.
Уравнение \eqref{ref3} называется векторным параметрическим уравнением прямой, а переменная величина \(t\), принимающая любые вещественные значения, называется параметром.
Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.
Рассмотрим прямую в пространстве. Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\), соответственно, а вектор \(\boldsymbol{a}\) имеет компоненты \((a_{1}, a_{2}, a_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref3}, мы получим
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t,\ z-z_{0} = a_{3}t.\label{ref4}
$$
Для прямой на плоскости мы получаем, аналогично,
$$
x-x_{0} = a_{1}t,\ y-y_{0} = a_{2}t.\label{ref5}
$$
Уравнения \eqref{ref4} или \eqref{ref5} называются параметрическими уравнениями прямой.
Получим теперь параметрические уравнения плоскости. Обозначим через \(\boldsymbol{p}\) и \(\boldsymbol{q}\) ее направляющие векторы, а через \(\boldsymbol{r}_{0}\) — радиус-вектор ее начальной точки \(M_{0}\). Пусть точка \(M\) с радиус-вектором \(\boldsymbol{r}\) — произвольная точка пространства (рис. 6.2).
Рис. 6.2
Вектор \(\overrightarrow{M_{0}M} = \boldsymbol{r}-\boldsymbol{r}_{0}\), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец \(M\) также лежит на плоскости. Так как \(\boldsymbol{p}\) и \(\boldsymbol{q}\) не коллинеарны, в этом и только этом случае \(\boldsymbol{r}-\boldsymbol{r}_{0}\) может быть по ним разложен. Поэтому, если точка \(M\) лежит в плоскости (и только в этом случае), найдутся такие числа \(t_{1}\) и \(t_{2}\), что
$$
\boldsymbol{r}-\boldsymbol{r}_{0} = t_{1}\boldsymbol{p}+t_{2}\boldsymbol{q}.\label{ref6}
$$
Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров \(t_{1}\) и \(t_{2}\). Наоборот, какие бы числа мы ни подставили как значения \(t_{1}\) и \(t_{2}\), уравнение \eqref{ref6} определит некоторую точку плоскости.
Пусть \((x, y, z)\) и \((x_{0}, y_{0}, z_{0})\) — координаты точек \(M\) и \(M_{0}\) соответственно, а векторы \(\boldsymbol{p}\) и \(\boldsymbol{q}\) имеют компоненты \((p_{1}, p_{2}, p_{3})\) и \((q_{1}, q_{2}, q_{3})\). Тогда, раскладывая по базису обе части уравнения \eqref{ref6}, мы получим параметрические уравнения плоскости
$$
x-x_{0} = t_{1}p_{1}+t_{2}q_{1},\ y-y_{0} = t_{1}p_{2}+t_{2}q_{2},\ z-z_{0} = t_{1}p_{3}+t_{2}q_{3}.\label{ref7}
$$
Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра \(t\), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.































