Метод наименьших квадратов: примеры решений задач

Графический метод: подготовка

Интерполяция в Excel в таком случае начинается с построения графика. Для этого:

• во вкладке «Вставка» выделяют табличный диапазон;
• в блоке инструментов «Диаграммы» выбирают значок «График»;
• в появившемся списке выбирают тот, который лучше подходит для решения конкретной задачи.

Так как в ячейке B9 пусто, график получился разорванный. Кроме того, на нем присутствует дополнительная линия X, в которой нет необходимости, а на горизонтальной оси вместо значений аргумента указаны пункты по порядку.

Интерполяция функции нескольких переменных
Выполнив формирование таблицы, приведённой на рис. 8, по формулам (17) и (11) можно вычислить значение интерполируемой функции для любого значения аргумента Х. Например, дляХ=1 вычисляем значенияli(1) (i=0,1,2,3):

Метод наименьших квадратов

В Excel, как известно, существует встроенная функция автосуммы, позволяющая вычислить значения всех значений, расположенных в выделенном диапазоне. Таким образом, ничто не помешает нам рассчитать значение выражения (e 1 2 + e 2 2 + e 3 2 + … e n 2).

В математической записи это имеет вид:

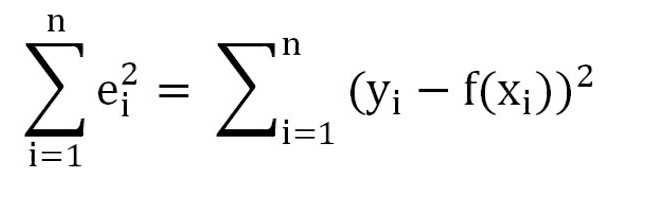
Так как изначально было принято решение об аппроксимировании с помощью прямой, то имеем:

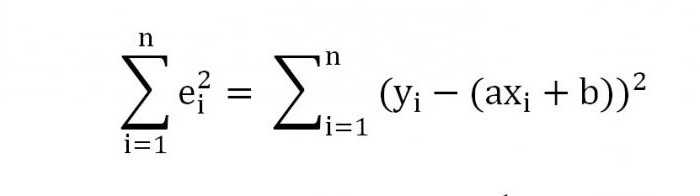
Таким образом, задача нахождения прямой, которая лучше всего описывает конкретную зависимость величин X и Y, сводится к вычислению минимума функции двух переменных:

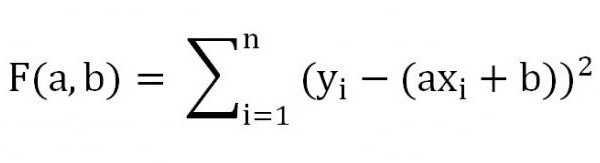
Для этого требуется приравнять к нулю частные производные по новым переменным a и b, и решить примитивную систему, состоящую из двух уравнений с 2-мя неизвестными вида:

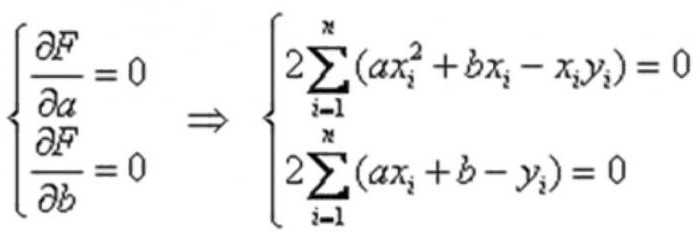
После нехитрых преобразований, включая деление на 2 и манипуляции с суммами, получим:

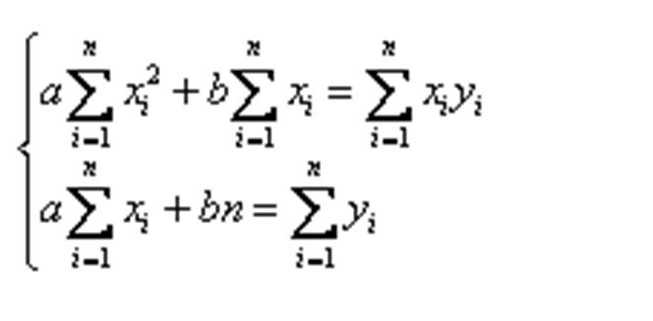
Решая ее, например, методом Крамера, получаем стационарную точку с некими коэффициентами a * и b * . Это и есть минимум, т. е. для предсказания, какой товарооборот будет у магазина при определенной площади, подойдет прямая y = a * x + b * , представляющая собой регрессионную модель для примера, о котором идет речь. Конечно, она не позволит найти точный результат, но поможет получить представление о том, окупится ли покупка в кредит магазина конкретной площади.

3.1. Зачем нужна аппроксимация функций?

В окружающем нас мире все взаимосвязано, поэтому одной из наиболее часто встречающихся задач является установление характера зависимости между различными величинами, что позволяет по значению одной величины определить значение другой. Математической моделью зависимости одной величины от другой является понятие функции
y=f(x)
.

В практике расчетов, связанных с обработкой экспериментальных данных, вычислением
f(x),
разработкой вычислительных методов, встречаются следующие две ситуации:

1. Как установить вид функции
y=f(x),
если она неизвестна? Предполагается при этом, что задана таблица ее значений, которая получена либо из экспериментальных измерений, либо из сложных расчетов.

2. Как упростить вычисление известной функции
f(x)
или же ее характеристик, если
f(x)
слишком сложная?

Ответы на эти вопросы даются теорией аппроксимации функций,
основная задача
которой состоит в нахождении функции
y=

(x)
, близкой (т.е. аппроксимирующей) в некотором нормированном пространстве к исходной функции
y=f(x).
Функцию

(x)
при этом выбирают такой, чтобы она была максимально удобной для последующих расчетов.

Основной подход
к решению этой задачи заключается в том, что

(x)
выбирается зависящей от нескольких свободных параметров, т.е. , значения которых подбираются из некоторого условия близости
f(x)
и

(x)
.

Обоснование способов нахождения удачного вида функциональной зависимости и подбора параметров составляет задачу
теории аппроксимации функций
.

В зависимости от способа подбора параметров получают различные
методы аппроксимации;
наибольшее распространение среди них получили
интерполяция
и
среднеквадратичное приближение,
частным случаем которого является
метод наименьших квадратов.

Наиболее простой, хорошо изученной и нашедшей широкое применение в настоящее время является
линейная аппроксимация
,
при которой выбирают функцию, линейно зависящую от параметров, т.е. в виде обобщенного многочлена:

. (3.1)

Здесь известная система линейно независимых (базисных) функций. В качестве в принципе могут быть выбраны любые элементарные функции, например: тригонометрические, экспоненты, логарифмические или комбинации таких функций

Важно, чтобы система базисных функций была
полной
, т.е. обеспечивающей аппроксимацию
f(x)
многочленом (3.1) с заданной точностью при.. Приведем хорошо известные и часто используемые системы

При интерполяции обычно используется система линейно независимых функций. Для среднеквадратичной аппроксимации удобнее в качестве брать ортогональные на интервале многочлены Лежандра:

Приведем хорошо известные и часто используемые системы. При интерполяции обычно используется система линейно независимых функций. Для среднеквадратичной аппроксимации удобнее в качестве брать ортогональные на интервале многочлены Лежандра:

Заметим, что если функция задана на отрезке
,
то при использовании этой системы необходимо предварительно осуществить преобразование координат, приводящее интервал к интервалу.

Для аппроксимации периодических функций используют ортогональную на систему тригонометрических функций. В этом случае обобщенный многочлен (3.1) записывается в виде.

Классификация методов наименьших квадратов

1. Метод наименьших квадратов.
2. Метод максимального правдоподобия (для нормальной классической линейной модели регрессии постулируется нормальность регрессионных остатков).
3. Обобщенный метод наименьших квадратов ОМНК применяется в случае автокорреляции ошибок и в случае гетероскедастичности.
4. Метод взвешенных наименьших квадратов (частный случай ОМНК с гетероскедастичными остатками).

Проиллюстрируем суть классического метода наименьших квадратов графически
. Для этого построим точечный график по данным наблюдений (x i , y i , i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.
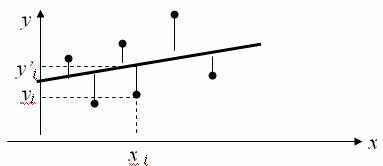Математическая запись данной задачи: .
Значения y i и x i =1…n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров — , . Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е. .
В результате получим систему из 2-ух нормальных линейных уравнений: Решая данную систему, найдем искомые оценки параметров:
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм (возможно некоторое расхождение из-за округления расчетов).
Для расчета оценок параметров , можно построить таблицу 1.
Знак коэффициента регрессии b указывает направление связи (если b >0, связь прямая, если b Формально значение параметра а – среднее значение y при х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла.

Оценка тесноты связи между признаками

осуществляется с помощью коэффициента линейной парной корреляции — r x,y .
Он может быть рассчитан по формуле: . Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: .
Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если r x, y >0, то связь прямая; если r x, y Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице ê r x , y ê =1, то связь между признаками функциональная линейная.
Если признаки х и y линейно независимы, то r x,y близок к 0.
Для расчета r x,y можно использовать также таблицу 1.

Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации – R 2 yx:
,
где d 2 – объясненная уравнением регрессии дисперсия y ;
e 2 — остаточная (необъясненная уравнением регрессии) дисперсия y ;
s 2 y — общая (полная) дисперсия y .
Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y , объясняемую регрессией (а, следовательно, и фактором х), в общей вариации (дисперсии) y . Коэффициент детерминации R 2 yx принимает значения от 0 до 1. Соответственно величина 1-R 2 yx характеризует долю дисперсии y , вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации.
При парной линейной регрессии R 2 yx =r 2 yx .

Линейная зависимость

Нас интересует связь 2-х переменных

х

и

y

. Имеется предположение, что

y

зависит от

х

по линейному закону

y

=

ax

+

b

. Чтобы определить параметры этой взаимосвязи исследователь провел наблюдения: для каждого значения х
i
произведено измерение y
i
(см.

файл примера
). Соответственно, пусть имеется 20 пар значений (х
i
; y
i).

Примечание:

Если шаг изменения по

х


постоянен, то для построения

диаграммы рассеяния

можно использовать
, если нет, то необходимо использовать тип диаграммы

Точечная

.

Из диаграммы очевидно, что связь между переменными близка к линейной. Чтобы понять какая из множества прямых линий наиболее «правильно» описывает зависимость между переменными, необходимо определить критерий, по которому будут сравниваться линии.

В качестве такого критерия используем выражение:

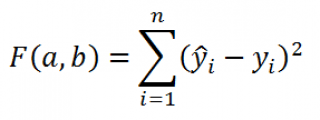
где

ŷ

i

=

a

*

x
i

+

b

;

n – число пар значений (в нашем случае n=20)

Вышеуказанное выражение представляет собой сумму квадратов расстояний между наблюденными значениями y
i
и ŷ
i
и часто обозначается как SSE (
Sum

of

Squared

Errors

(
Residuals
), сумма квадратов ошибок (остатков)
)

.

Метод наименьших квадратов

заключается в подборе такой линии

ŷ

=

ax

+

b

, для которой вышеуказанное выражение принимает минимальное значение.

Примечание:

Любая линия в двухмерном пространстве однозначно определяется значениями 2-х параметров:

a


(наклон) и

b


(сдвиг).

Считается, что чем меньше сумма квадратов расстояний, тем соответствующая линия лучше аппроксимирует имеющиеся данные и может быть в дальнейшем использована для прогнозирования значений y от переменной х. Понятно, что даже если в действительности никакой взаимосвязи между переменными нет или связь нелинейная, то МНК все равно подберет «наилучшую» линию. Таким образом, МНК ничего не говорит о наличии реальной взаимосвязи переменных, метод просто позволяет подобрать такие параметры функции

a


и

b


, для которых вышеуказанное выражение минимально.

Проделав не очень сложные математические операции (подробнее см.
), можно вычислить параметры

a


и

b


:

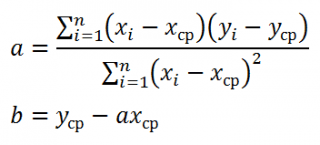
Как видно из формулы, параметр

a


представляет собой отношение ковариации и
, поэтому в MS EXCEL для вычисления параметра

а


можно использовать следующие формулы (см.

файл примера лист Линейная
):

=

КОВАР(B26:B45;C26:C45)/ ДИСП.Г(B26:B45)

или

=

КОВАРИАЦИЯ.В(B26:B45;C26:C45)/ДИСП.В(B26:B45)

Также для вычисления параметра

а


можно использовать формулу =

НАКЛОН(C26:C45;B26:B45)

. Для параметра

b


используйте формулу =

ОТРЕЗОК(C26:C45;B26:B45)

.

И наконец, функция

ЛИНЕЙН()

позволяет вычислить сразу оба параметра. Для ввода формулы

ЛИНЕЙН(C26:C45;B26:B45)

необходимо выделить в строке 2 ячейки и нажать

CTRL

+

SHIFT

+

ENTER

(см. статью про
). В левой ячейке будет возвращено значение

а


, в правой –

b


.

Примечание

: Чтобы не связываться с вводом

формул массива

потребуется дополнительно использовать функцию

ИНДЕКС()

. Формула =

ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);1)

или просто =

ЛИНЕЙН(C26:C45;B26:B45)

вернет параметр, отвечающий за наклон линии, т.е.

а


. Формула =

ИНДЕКС(ЛИНЕЙН(C26:C45;B26:B45);2)

вернет параметр, отвечающий за пересечение линии с осью Y, т.е.

b


.

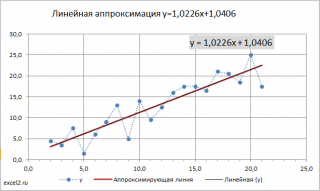
Вычислив параметры, на

диаграмме рассеяния

можно построить соответствующую линию.

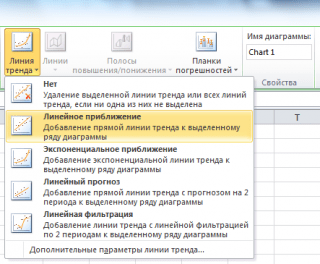
Еще одним способом построения прямой линии по методу наименьших квадратов является инструмент диаграммы

Линия тренда

. Для этого выделите диаграмму, в меню выберите

вкладку Макет

, в

группе Анализ

нажмите

Линия тренда

, затем

Линейное приближение

.

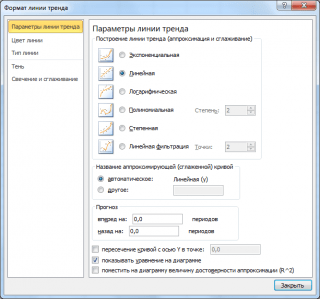
Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме.

Примечание

: Для того, чтобы параметры совпадали необходимо, чтобы тип у диаграммы был
. Дело в том, что при построении диаграммы

График

значения по оси Х не могут быть заданы пользователем (пользователь может указать только подписи, которые не влияют на расположение точек). Вместо значений Х используется последовательность 1; 2; 3; … (для нумерации категорий). Поэтому, если строить

линию тренда

на диаграмме типа

График

, то вместо фактических значений Х будут использованы значения этой последовательности, что приведет к неверному результату (если, конечно, фактические значения Х не совпадают с последовательностью 1; 2; 3; …).

Он имеет множество применений, так как позволяет осуществлять приближенное представление заданной функции другими более простыми. МНК может оказаться чрезвычайно полезным при обработке наблюдений, и его активно используют для оценки одних величин по результатам измерений других, содержащих случайные ошибки. Из этой статьи вы узнаете, как реализовать вычисления по методу наименьших квадратов в Excel.

Решение МНК

Мы ищем уравнение линейной регрессии, которое выглядит так: y = ax + b

Где:

• y – зависимая переменная
• x – независимая переменная
• a – коэффициент (это также наклон/градиент линии)
• b – коэффициент (это также точка, где линия пересекает ось Y)

Метод 1

Шаги, которые мы будем делать для поиска y = ax + b (сейчас мы их все пройдём на примере):

Шаг 1: Для каждой точки (x, y) вычислить x² и xy.

Шаг 2: Суммировать все x, y, x² и xy, это даст нам Σx, Σy, Σx² и Σxy (если кто забыл, Σ означает «сумма»).

Шаг 3: Рассчитать наклон a по этой формуле:

, где N – количество данных

Шаг 4: Рассчитать значение числа b:

, где N – количество данных

Шаг 5: Подставить найденные числа по местам в уравнение (y = ax + b)

Пример

После некоторых наблюдений, у нас появились данные о размерах и продажах некой торговой сети, у которой 5 магазинов:

Размер (x)	Продажи (y)
2	4
3	6
5	8
7	10
9	12

Для наглядности, например, это магазины мороженого, и 2-метровая лавочка продаёт в месяц 4 тонны мороженого, 7 метровая — 10 тонн.

Шаг 1:

Сразу можно записать, что N = 5 (количество данных; т.е. всего у нас данные по пяти магазинам, ведь у нас 5 строк данных).

Для каждой точки (x, y) вычисляем x² и xy. Для этого, к уже существующим столбцам добавим ещё два: x² и xy.

• x² получим путём возведения x (Размер) в квадрат
• xy получим путём умножения одного на второе

x	y	x²	xy
2	4	2² = 4	2 × 4 = 8
3	6	3² = 9	3 × 6 = 18
5	8	25	40
7	10	49	70
9	12	81	108

Шаг 2: Суммировать все x, y, x² и xy, это даст нам Σx, Σy, Σx² и Σxy (складываем каждый столбик):

x	y	x²	xy
2	4	2² = 4	2 × 4 = 8
3	6	3² = 9	3 × 6 = 18
5	8	25	40
7	10	49	70
9	12	81	108
Σx = 26	Σy = 40	Σx² = 168	Σxy = 244

Шаг 3: Рассчитать a (наклон графика) по этой формуле:

, где N – количество данных

Помним, что N = 5, значит:

Шаг 4: Рассчитать значение числа b:

, где N – количество данных

Помним, что N = 5, значит:

Шаг 5: Подставить найденные числа по местам в уравнение

y = ax + b ⇒ y = 1,0976x + 2,29248

Готово!

Далее можем проверить. Можем составить вот такой график, вместе с данными точками и полученной функцией:

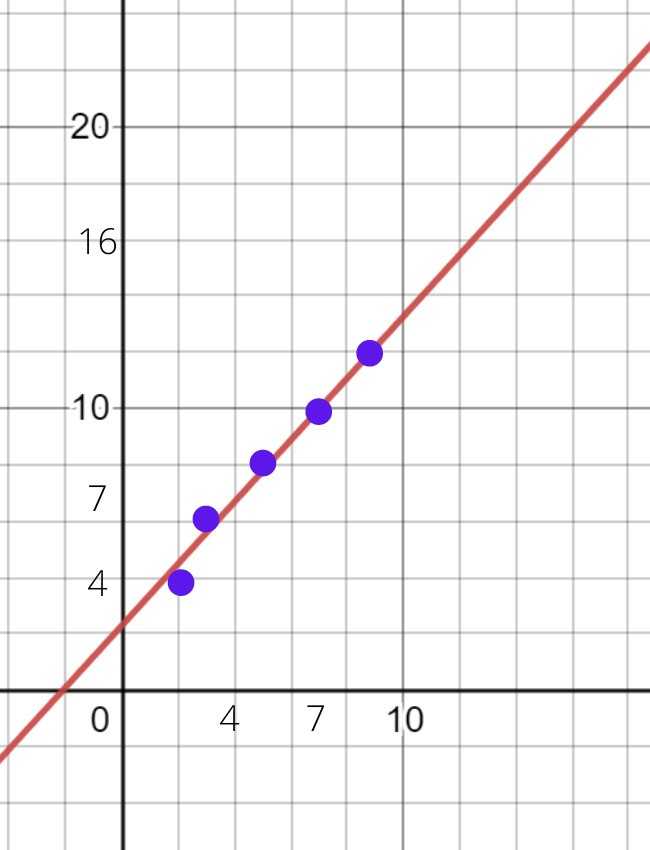Действительно, полученная функция и точки «ходят рука об руку».

Также мы можем использовать эту функцию, чтобы понять, как будут зависеть продажи фирмы от размера помещения. Например: руководство хочет открыть магазин размером в 11,5 м². Для этого подставляем 11,5 вместо x:

y = 1,0976x + 2,29248 ⇒ y = 1,0976 × 11,5 + 2,29248 = 14,91488

Ответ: этот магазин размером в 11,5 м² будет продавать около 15 тонн мороженого в месяц.

Метод 2

Мы продолжаем искать уравнение линейной регрессии, которое выглядит так: y = ax + b.

Используем тот же пример с сетью магазинов.

Размер (x)	Продажи (y)
2	4
3	6
5	8
7	10
9	12

Шаг 1: Опять суммируем все x, y, x² и xy, т.е. находим Σx, Σy, Σx² и Σxy (складываем каждый столбик):

x	y	x²	xy
2	4	2² = 4	2 × 4 = 8
3	6	3² = 9	3 × 6 = 18
5	8	25	40
7	10	49	70
9	12	81	108
Σx = 26	Σy = 40	Σx² = 168	Σxy = 244

Шаг 2: Записать вот такую систему уравнений (так мы будем искать параметры a и b):

Шаг 3: Помним, что N = 5. Таким образом, из нашего примера получаем систему:

Лучше конечно её переписать красиво:

Шаг 4: Решить систему.

Находим a = 1,0976; b = 2,29248; и ставим по местам в функцию (y = ax + b). Получается y = 1,0976x + 2,29248

Готово!

Для проверки лучше составить график с данными точками и найденной функцией, как в методе 1.

Узнайте также про Метод Крамера, Стандартное отклонение и Корреляции.

Шаг второй: решение задачки с использованием МНК

Пошаговое руководство выглядит следующим образом:

1. Столбику, который располагается левее показателя Х, даем название N и прописываем единицу рядом с 1-м показателем колонки Х. Единица – это примерное значение 1-го коэффициента N.

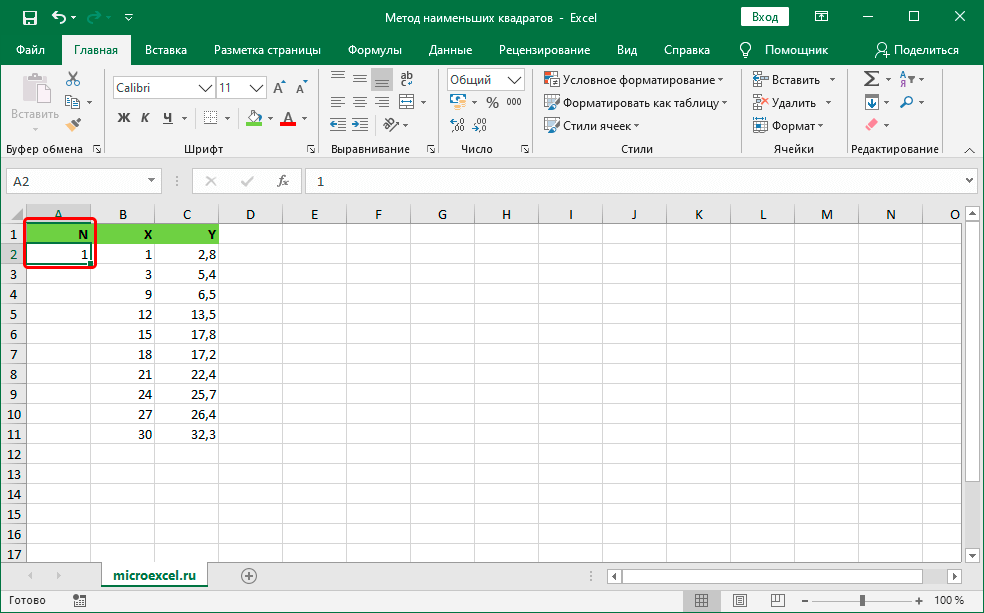6

1. Столбику, который располагается правее показателя Y, даем наименование NX.
2. В ячейку D1, находящуюся около первых показателей X и Y, прописываем специальную формулу произведения коэффициента N на показатель из столбика Х. Сама формула выглядит следующим образом: =$А$2*В2. Стоит заметить, что адрес ячейки с коэффициентом необходимо привести к абсолютному типу. Абсолютный тип в табличном процессоре позволяет зафиксировать строчку или столбик (или все вместе одновременно). Иными словами, при копировании значений в другие ячейки абсолютные ссылки не будут меняться. После проведения всех манипуляций жмем клавишу «Enter».

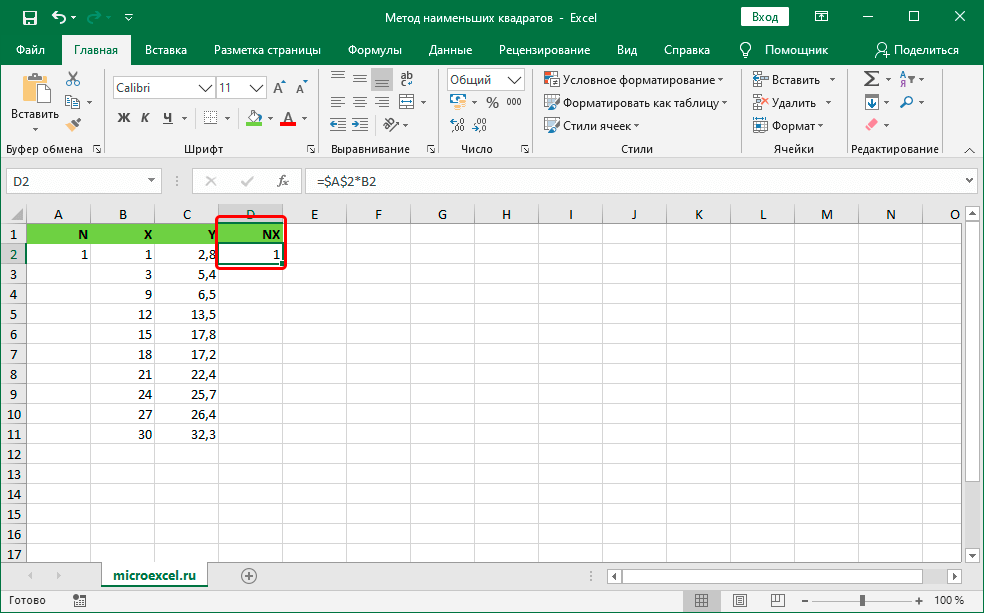7

1. Перемещаем курсор мышки на сектор с выведенным результатом. Наведя указатель в правый верхний уголок, он превратится в маленький плюсик темного цвета, который называется маркером заполнения. Зажимаем ЛКМ и перетягиваем маркер в самый низ до крайней строчки табличных данных.

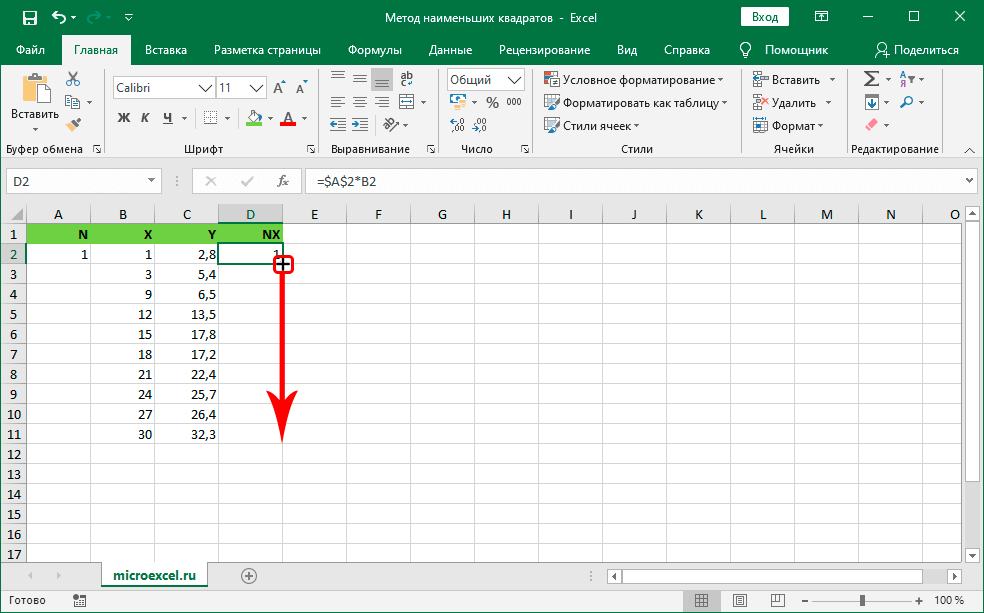8

1. После проведения этих манипуляций мы получили результаты вычислений во всех секторах колонки NX.

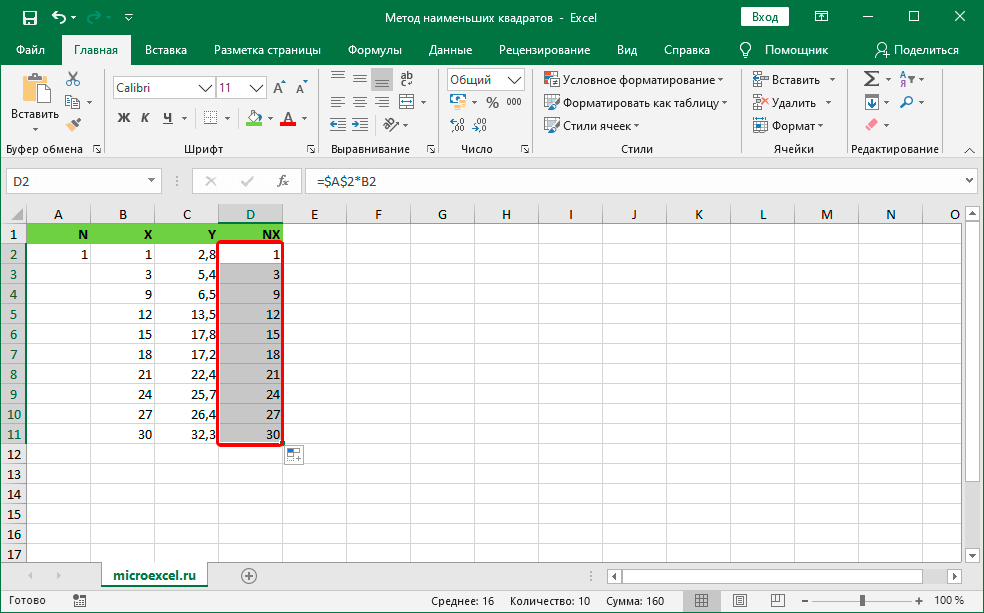9

1. Далее переходим к подсчету суммы разностей квадратов показателей Y и NX. Перемещаемся в ячейку E1, располагающуюся правее от показателя NX, нажимаем на элемент «Вставить функцию», который находится рядом со строкой для ввода формул, и имеет внешний вид «fx».

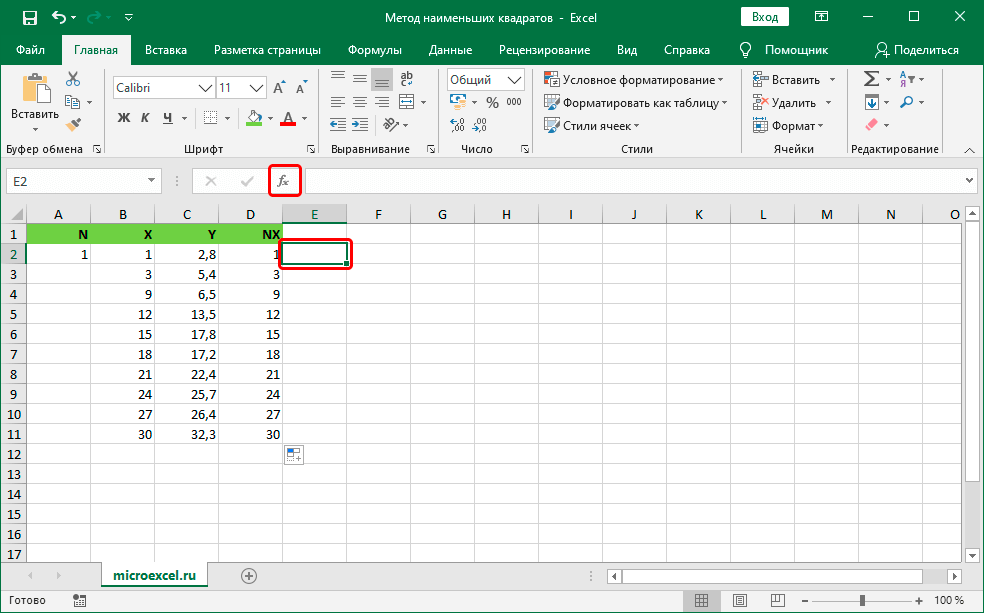10

1. Первым делом, находим надпись «Категории:» и раскрываем список, находящийся рядом. В обширном списке выбираем элемент «Математические». В блоке «Выберите функцию:» отыскиваем функцию «СУММКВРАЗН» и выбираем ее. После проведения всех манипуляций жмем на кнопку «ОК».

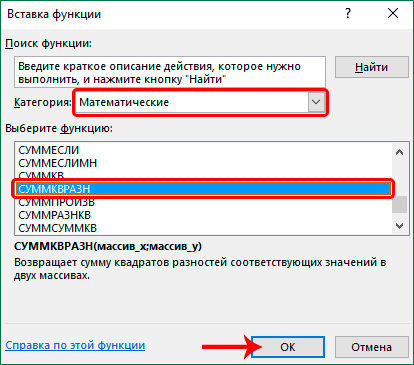11

1. Открылось небольшое окошко «Аргументы функции». Для дальнейшей работы необходимо заполнить все строки формы. В строчку «Массив_х» вводим адрес диапазона ячеек столбика Y. Координаты можно вписать самостоятельно ручным вводом, используя клавиатуру, или же путем их выбора в самих табличных данных.
2. В строчку «Массив_у» вводим адрес диапазона ячеек столбика NX. После проведения всех манипуляций щёлкаем клавишу «Enter».

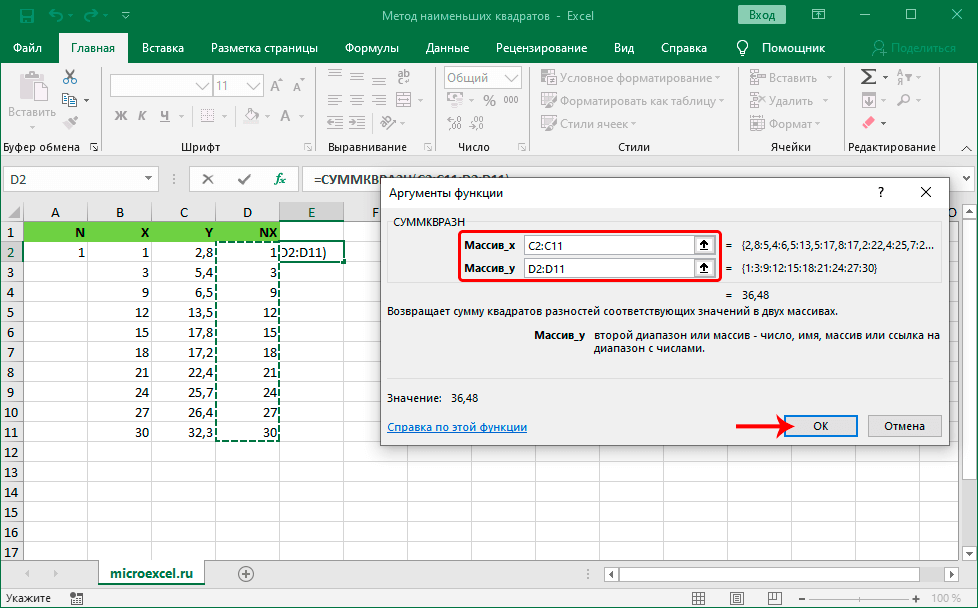12

1. Перемещаемся в раздел «Данные», который находится в верхней части интерфейса табличного процессора. Находим блок команд под названием «Анализ» и выбираем элемент «Поиск решения».

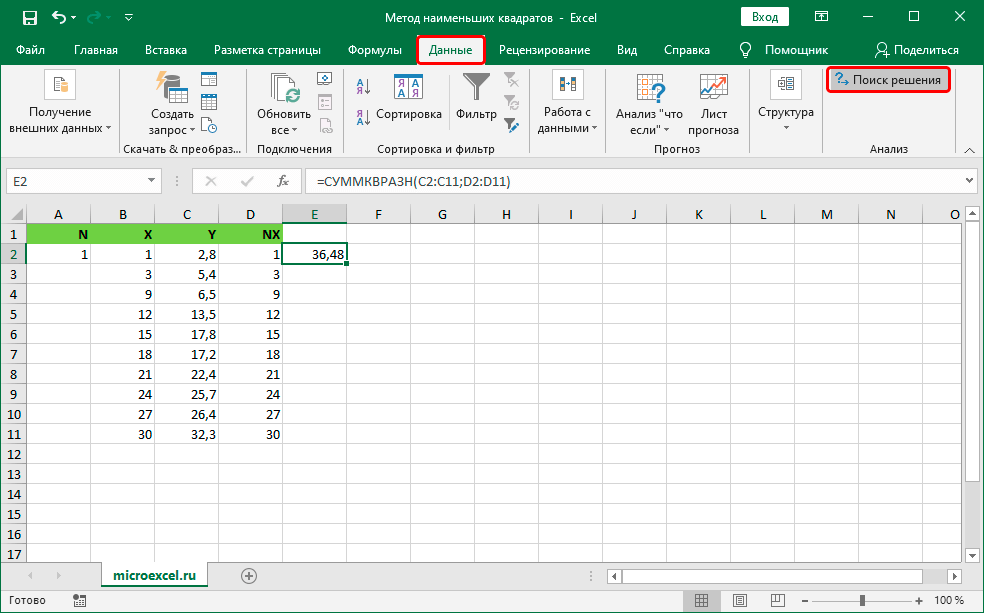13

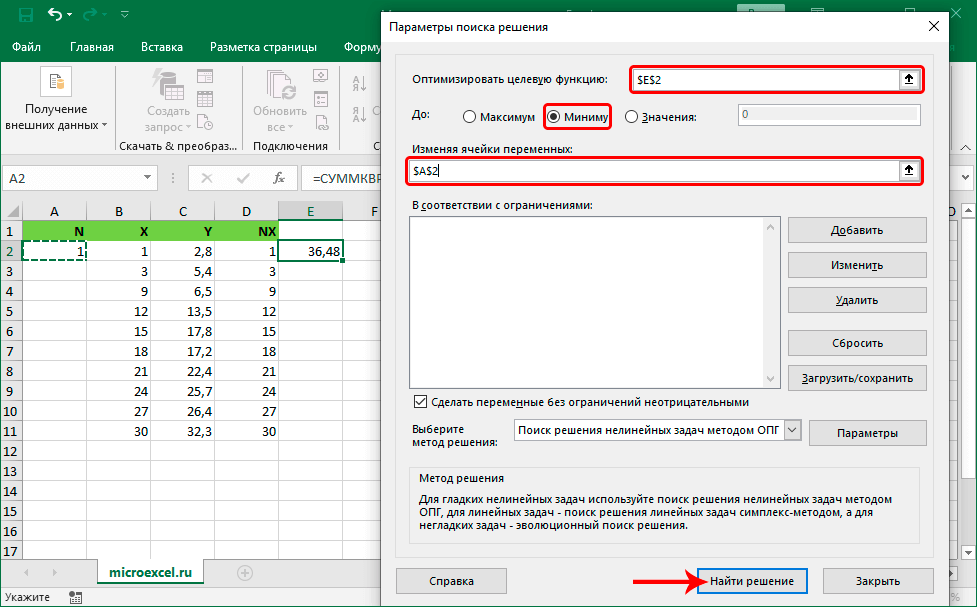
1. На экране отобразилось окошко с огромным количеством настроек, которые необходимо заполнить. В строчку «Оптимизировать целевую функцию» вводим ссылку на ячейку с оператором «СУММКВРАЗН». Реализовать это действие можно самостоятельно ручным вводом, используя клавиатуру, или же выбрав сектор в самой табличке. Ставим отметку около надписи «Минимум», которая располагается в блоке «До:». В строчку «Изменяя ячейки переменных» вбиваем адрес сектора, в котором располагается показатель коэффициента N – $A$2. После проведения всех манипуляций щелкаем на «Найти решение».

14

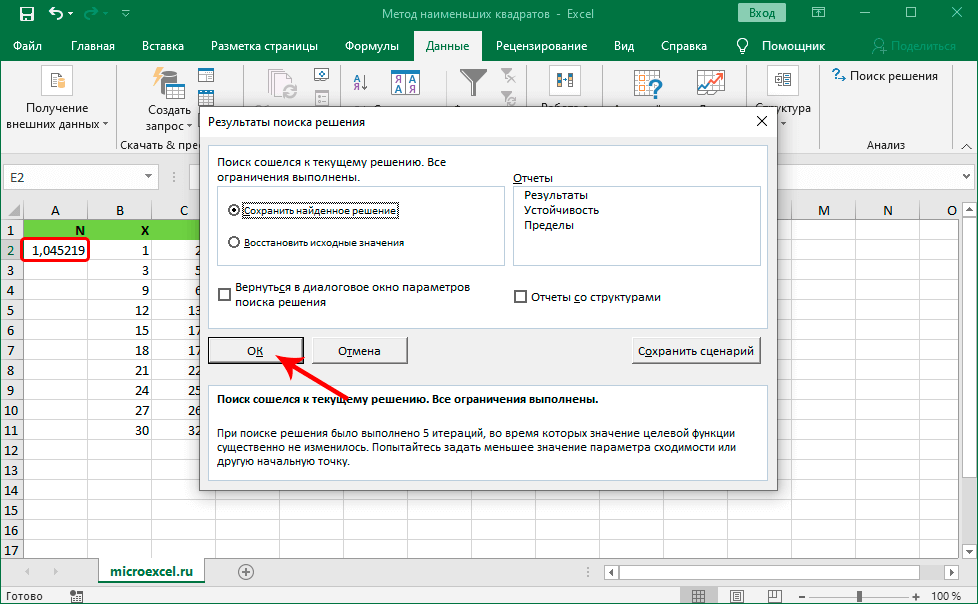
1. После того, как «Поиск решения» будет выполнен, на экране компьютера отобразится окошко с выведенными результатами поиска решения, а затем реализуется замена числовых значений в столбике N. Отображенный результат – это наименьший квадрат функции. Если выведенный результат удовлетворяет тому, что нужно было найти, то нажимаем «ОК».

15

МНК: Приближение полиномом в EXCEL

Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).

В основной статье про МНК было рассмотрено приближение линейной функцией. В этой статье рассмотрим приближение полиномиальной функцией (с 3-й до 6-й степени) следующего вида: y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +…+b ₆ x 6

Примечание : В инструменте MS EXCEL Линия тренда , который доступен для диаграмм типа Точечная и График , можно построить линию тренда на основе полинома с максимальной степенью 6. В файле примера продемонстрировано полное совпадение линии тренда диаграммы и линии, вычисленной с помощью формул.

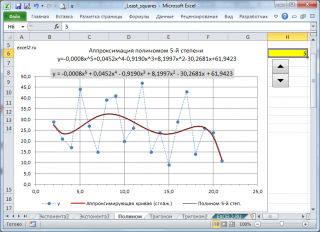
Покажем, как вычислить коэффициенты b линии тренда, заданной полиномом.

Как известно, квадратичная зависимость y=b +b ₁ x+b ₂ x 2 , подробно рассмотренная в статье МНК: Квадратичная зависимость в MS EXCEL , является частным случаем полиномиальной y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +… зависимости (в этом случае степень полинома равна 2). Соответственно, используя тот же подход (приравнивание к 0 частных производных), можно вычислить коэффициенты любого полинома.

Примечание : Существует еще один метод вычисления коэффициентов – замена переменных, который рассмотрен в конце статьи.

Для нахождения m+1 коэффициента полинома m-й степени составим систему из m+1 уравнения и решим ее методом обратной матрицы . Для квадратного уравнения (m=2) нам потребовалось вычислить сумму значений х с 1-й до 4-й степени, а для полинома m-й степени необходимо вычислить значения х с 1-й до 2*m степени.

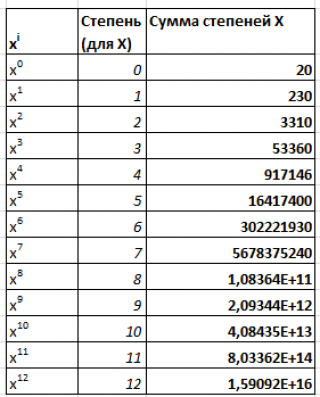
Примечание : Для удобства суммы степеней значений х можно вычислить в отдельном диапазоне ( файл примера столбцы К:М).

В файле примера создана универсальная форма для вычисления коэффициентов полиномов.

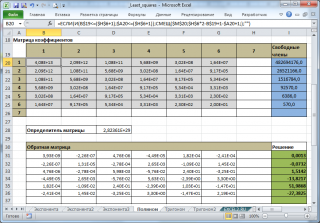
Выбрав с помощью элемента управления Счетчик нужную степень полинома, автоматически получим аппроксимацию наших данных выбранным полиномом (будет построен соответствующий график).

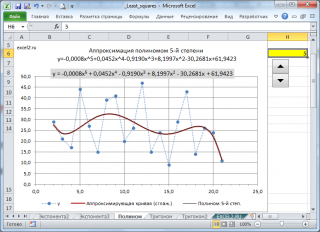
Примечание: При использовании полиномов высокой степени необходимо следить за тем, чтобы количество пар значений (х _i ; y _i ) превышало степень полинома хотя бы на несколько значений (для обеспечения точности аппроксимации). Кроме того, график функции полинома степени m имеет m-1 точку перегиба. Понятно, что точек данных должно быть гораздо больше, чем точек перегиба, чтобы такой изменчивый тренд стал очевидным (если утрировать, то бессмысленно строить по двум точкам параболу, логичнее построить прямую).

Как видно из расчетов, в MS EXCEL этот путь является достаточно трудоемким. Гораздо проще в MS EXCEL реализовать другой подход для вычисления коэффициентов полинома — с помощью замены переменных.

С помощью замены переменных x i =x _i полиномиальную зависимость y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +… можно свести к линейной. Теперь переменная y зависит не от одной переменной х в m разных степенях, а от m независимых переменных x _i . Поэтому для нахождения коэффициентов полинома мы можем использовать функцию ЛИНЕЙН() . Этот подход также продемонстрирован в файле примера .

Алгебраический метод наименьших квадратов

Под алгебраическим методом наименьших квадратов понимается метод решения систем линейных уравнений

путем минимизации евклидовой нормы

Ax ? b? > inf . (1.2)

Анализ данных эксперимента

Рассмотрим некоторый эксперимент, в ходе которого в моменты времени

производится, например, измерение температуры Q(t). Пусть результаты измерений задаются массивом

Допустим, что условия проведения эксперимента таковы, что измерения проводятся с заведомой погрешностью. В этих случаях закон изменения температуры Q(t) ищут с помощью некоторого полинома

P(t) = + + + … +,

определяя неизвестные коэффициенты, …, из тех соображений, чтобы величина E(, …,), определяемая равенством

гаусс алгебраический exel аппроксимация

принимала минимальное значение. Поскольку минимизируется сумма квадратов, то этот метод называется аппроксимацией данных методом наименьших квадратов.

Если заменить P(t) его выражением, то получим

Поставим задачу определения массива так, чтобы величина была минимальна, т.е. определим массив методом наименьших квадратов. Для этого приравняем частные производные пок нулю:

Если ввести m Ч n матрицу A = (), i = 1, 2…, m; j = 1, 2, …, n, где

I = 1, 2…, m; j = 1, 2, …, n,

то выписанное равенство примет вид

Перепишем написанное равенство в терминах операций с матрицами. Имеем по определению умножения матрицы на столбец

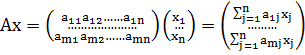
Для транспонированной матрицы аналогичное соотношение выглядит так

Введем обозначение: i -ую компоненту вектора Ax будем обозначать В соответствии с выписанными матричными равенствами будем иметь

В матричной форме это равенство перепишется в виде

A T x=A T B (1.3)

Здесь A — прямоугольная mЧ n матрица. Причем в задачах аппроксимации данных, как правило, m > n. Уравнение (1.3) называется нормальным уравнением.

Можно было с самого начала, используя евклидову норму векторов, записать задачу в эквивалентной матричной форме:

Наша цель минимизировать эту функцию по x. Для того чтобы в точке решения достигался минимум, первые производные по x в этой точке должны равняться нулю. Производные данной функции составляют

2A T B + 2A T Ax

и поэтому решение должно удовлетворять системе линейных уравнений

(A T A)x = (A T B).

Эти уравнения называются нормальными уравнениями. Если A — mЧ n матрица, то A>A — n Ч n — матрица, т.е. матрица нормального уравнения всегда квадратная симметричная матрица. Более того, она обладает свойством положительной определенности в том смысле, что (A>Ax, x) = (Ax, Ax) ? 0.

Замечание. Иногда решение уравнения вида (1.3) называют решением систе- мы Ax = В, где A прямоугольная m Ч n (m > n) матрица методом наименьших квадратов.

Задачу наименьших квадратов можно графически интерпретировать как минимизацию вертикальных расстояний от точек данных до модельной кривой (см. рис.1.1). Эта идея основана на предположении, что все ошибки в аппроксимации соответствуют ошибкам в наблюдениях. Если имеются также ошибки в независимых переменных, то может оказаться более уместным минимизировать евклидово расстояние от данных до модели.

Оценка точности

При любой аппроксимации особую важность приобретает оценка ее точности. Обозначим через e i разность (отклонение) между функциональными и экспериментальными значениями для точки x i , т. е

e i = y i — f (x i)

е. e i = y i — f (x i).

Очевидно, что для оценки точности аппроксимации можно использовать сумму отклонений, т. е. при выборе прямой для приближенного представления зависимости X от Y нужно отдавать предпочтение той, у которой наименьшее значение суммы e i во всех рассматриваемых точках. Однако, не все так просто, так как наряду с положительными отклонениями практически будут присутствовать и отрицательные.

Решить вопрос можно, используя модули отклонений или их квадраты. Последний метод получил наиболее широкое распространение. Он используется во многих областях, включая регрессионный анализ (в Excel его реализация осуществляется с помощью двух встроенных функций), и давно доказал свою эффективность.

Метод наименьших квадратов

В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей. 

Иными словами, из всего множества линий, линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной: 

следовательно 

Целью процедур линейной регрессии является подгонка прямой линии по точкам.

А именно, построить линию регрессии так, чтобы минимизировать квадраты отклонений этой линии от наблюдаемых точек.

Поэтому на эту общую процедуру иногда ссылаются как на оценивание по методу наименьших квадратов. Прямая линия на плоскости (в пространстве двух измерений) задается уравнением Y=ax+b 

Линейная функция

Зная зависимость между величинами, представленными в таблице и полученные опытным путем, необходимо составить математическую зависимость (функциональную зависимость). Воспользуемся методом наименьших квадратов. Пусть опытные данные, близкие к линейной функции,  записаны в таблицу вида:

X	x1	x2	x3	…	xn
Y	y1	y2	y3	…	yn

Подбираем y=ax+b таким образом, чтобы сумма квадратов отклонений была наименьшей. Чтобы найти минимум функции надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю.  Обозначим сумму квадратов отклонений (Σεi2) через S, тогда:

S зависит от a и b, т.е. функция двух переменных принимает наименьшее значение в стандартной точке, которая находится из условия:

 Приравняем каждую частную производную к нулю:

Формула для расчета линейной функции y=ax+b

Опытные данные:

i	Yi	Xi	X2i	YiXi
1	-8	-2	4	16
2	7	-1	1	-7
3	7
4	5	2	4	10
5	5	3,5	12,25	17,5
6	3,5	4	16	14
7	3	5	25	15
8	2,5	6	36	15
9	2	7	49	14
10	1,5	7	49	10,5
Σ	28,5	31,5	196,25	105

Для решения системы линейных уравнений и определения параметров, воспользуемся методом Крамера.

Уравнение прямой принимает следующий вид: y=0.1569X+2.3557

Всего один выброс (экстремальная точка с координатами -2; -8 на диаграмме рассеяния) может полностью изменить наклон регрессионной линии и, следовательно, вид зависимости между переменными.

Такие выбросы могут исказить оценки модели, сдвигая линию регрессии в определенном направлении и, тем самым, вызывая смещение коэффициентов регрессии.

  На случай появления выбросов, должны быть предусмотрены корректировки, основанные на использовании “принципов статистического контроля”, т. е.

значения, выходящие за определенный диапазон, который определяется в терминах, кратных сигма, т.е. стандартных отклонений, могут быть преобразованы или вовсе пропущены, и только после этого должны вычисляться окончательные оценки параметров модели (уравнения) регрессии. 

Квадратичная функция (парабола второго порядка) 

Рассмотрим модель регрессии, которая нелинейна относительно включённых в модель независимых переменных Xi, но линейна по оцениваемым параметрам a, b, c. К таким моделям относятся полиномы второго и выше  порядков, а также гиперболическая функция.

Квадратичную функцию вида 

подбираем таким образом, чтобы сумма квадратов отклонений была наименьшей. Чтобы найти минимум функции надо вычислить частные производные по каждому из параметров (а b c) и приравнять их к нулю. 

Обозначим сумму квадратов отклонений (Σεi2) через S, тогда сумма наименьших квадратов отклонений примет следующее выражение:

Функция трех переменных (a b c) принимает наименьшее значение в стандартной точке, которая находится из условия:

 Приравняем каждую частную производную к нулю:

Формула для расчета квадратичной функции y = ax2 + bx + c

Опытные данные:

i	Yi	Xi	Xi2	Xi3	Xi4	YiXi	YiXi2
1	4,3	-1	1	-1	1	-4,3	4,30
2	3	-0,8	0,64	-0,512	0,4096	-2,4	1,92
3	2
4	1,5	0,5	0,25	0,125	0,0625	0,75	0,375
5	1	1	1	1	1	1	1
6	0,8	1,8	3,24	5,832	10,4976	1,44	2,592
7	2,5	2	4	8	16	5	10
8	2,7	2,5	6,25	15,625	39,0625	6,75	16,875
9	3,5	2,6	6,76	17,576	45,6976	9,1	23,66
10	4,2	3,3	10,89	35,937	118,5921	13,86	45,738
∑	25,5	11,9	34,03	82,583	232,3219	31,2	106,46

Для решения системы линейных уравнений и определения параметров, воспользуемся методом Крамера.

Уравнение параболы 2-го порядка принимает следующий вид:

y=0.6531×2-1.3403x+1.9226

По предварительному анализу для данной модели (уравнения регрессии) выполняются первая и вторая предпосылки МНК: остатки распределены случайно, средняя величина случайного отклонения εi (остатков) для всех наблюдений равна нулю (-6,66134E-17 т.е. с точностью до 17 знака после запятой)

Решение системы линейных алгебраических уравнений (СЛАУ) и вычисление определителя матрицы в MS Excel решается с помощью  матричных функций.

Смотри также: